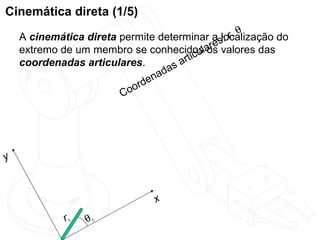
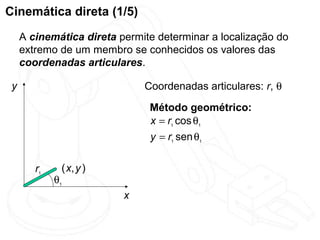
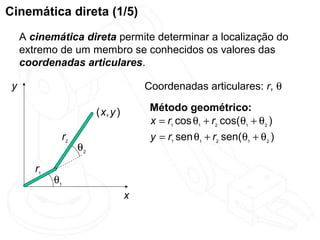
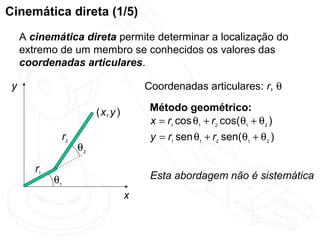
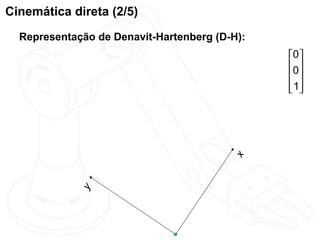
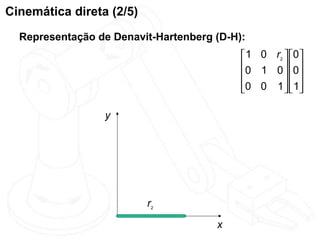
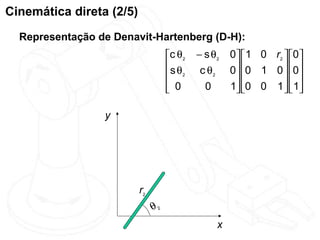
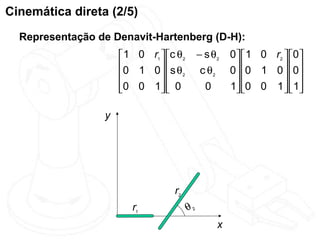
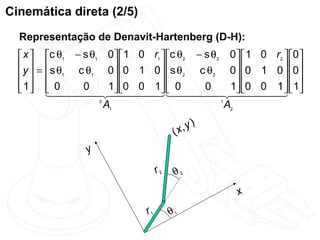
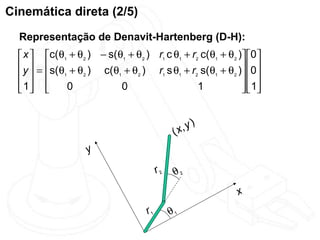
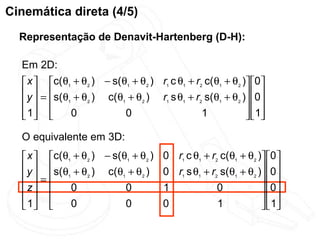
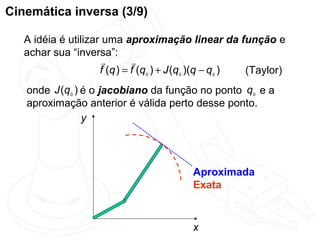
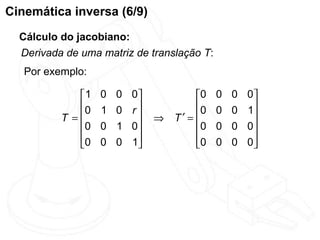
O documento discute cinemática direta e inversa de robôs. A cinemática direta determina a posição final de um robô dado seus ângulos de articulação, enquanto a cinemática inversa calcula os ângulos de articulação necessários para alcançar uma posição final específica. A representação de Denavit-Hartenberg é usada para descrever as transformações entre os elos de um robô. O jacobiano é calculado para aproximar linearmente a cinemática inversa.

1. CINEMÁTICA INVERSA
Aline Aparecida de Pina
Rodrigo Morante Blanco

2. Objetivos
•Cinemática direta
•Introdução
•Representação de Denavit-Hartenberg (D-H)
•Cinemática inversa
•Introdução
•Cálculo do jacobiano
•Inversa generalizada
•Transposta do jacobiano

3. Cinemática direta (1/5)
θ
A cinemática direta permite determinar a s: r,
localização do
e
extremo de um membro se conhecidoslar valores das
os
rticu
coordenadas articulares.
asa
nad
r de
C oo
y
x
r1 θ1

4. Cinemática direta (1/5)
A cinemática direta permite determinar a localização do
extremo de um membro se conhecidos os valores das
coordenadas articulares.
y Coordenadas articulares: r, θ
Método geométrico:
x = r1 cos θ1
y = r1 sen θ1
r1 ( x, y )
θ1
x

5. Cinemática direta (1/5)
A cinemática direta permite determinar a localização do
extremo de um membro se conhecidos os valores das
coordenadas articulares.
y Coordenadas articulares: r, θ
( x, y ) Método geométrico:
x = r1 cos θ1 + r2 cos( θ1 + θ2 )
r2 y = r1 sen θ1 + r2 sen( θ1 + θ2 )
θ2
r1
θ1
x

6. Cinemática direta (1/5)
A cinemática direta permite determinar a localização do
extremo de um membro se conhecidos os valores das
coordenadas articulares.
y Coordenadas articulares: r, θ
( x, y ) Método geométrico:
x = r1 cos θ1 + r2 cos( θ1 + θ2 )
r2 y = r1 sen θ1 + r2 sen( θ1 + θ2 )
θ2
r1
θ1 Esta abordagem não é sistemática
x

7. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
0
0
 
 1
 
x
y

8. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
 1 0 r2  0
0 1 0  0
  
0 0 1   1
  
y
r2
x

9. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
c θ2 − s θ2 0  1 0 r2  0
s θ c θ2 0 0 1 0  0
 2   
 0
 0 1 0 0 1   1
  
y
r2
θ2
x

10. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
 1 0 r1  c θ2 − s θ2 0  1 0 r2  0
0 1 0  s θ c θ2 0 0 1 0  0
  2   
0 0 1  0
  0 1 0 0 1   1
  
y
r2
r1 θ2
x

11. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
 x  c θ1 − s θ1 0 1 0 r1  c θ2 − s θ2 0  1 0 r2  0
 y  = s θ c θ1 0 0 1 0  s θ2 c θ2 0 0 1 0  0
   1     
 1  0
      0  1 0  1
0 1 0 0 1 
 0  0  
1
     
0
A1 1
A2
(x,y)
y
r2 θ2
x
r1 θ1

12. Cinemática direta (2/5)
Representação de Denavit-Hartenberg (D-H):
 x  c(θ1 + θ2 ) − s(θ1 + θ2 ) r1 c θ1 + r2 c(θ1 + θ2 ) 0
 y  = s(θ + θ ) c(θ + θ ) r s θ + r s(θ + θ ) 0
   1 2 1 2 1 1 2 1 2
 
 1 
   0 0 1   1
 
(x,y)
y
r2 θ2
x
r1 θ1

13. Cinemática direta (3/5)
Representação de Denavit-Hartenberg (D-H):
De esta forma é possível descrever as rotações e
translações de um elo do sistema com respeito ao elo
anterior. A extensão a 3D é imediata (acrescentado uma
linha e uma coluna). Por exemplo:
1 0 0 0
0 c θ − s θ 0
Rotação ao redor do eixo x:  
0 s θ c θ 0
0 0 0 1
 
1 0 0 0
0 1 0 0
Translação paralela ao eixo z:  
0 0 1 r
0 0 0 1
 

14. Cinemática direta (4/5)
Representação de Denavit-Hartenberg (D-H):
Em 2D:
 x  c(θ1 + θ2 ) − s(θ1 + θ2 ) r1 c θ1 + r2 c(θ1 + θ2 ) 0
 y  = s(θ + θ ) c(θ + θ ) r s θ + r s(θ + θ ) 0
   1 2 1 2 1 1 2 1 2
 
 1 
   0 0 1   1
 
O equivalente em 3D:
 x  c(θ1 + θ2 ) − s(θ1 + θ2 ) 0 r1 c θ1 + r2 c(θ1 + θ2 ) 0
 y  s(θ + θ ) c(θ + θ ) 0 r1 s θ1 + r2 s(θ1 + θ2 ) 0
 = 1 2 1 2
 
z   0 0 1 0  0
 1  0 0 0 1   1
    

15. Cinemática direta (5/5)
Representação de Denavit-Hartenberg (D-H):
Utilizando matrizes de transformação homogênea:
•Cada elo do sistema tem associado um sistema de
referência
•É possível representar as translações e rotações
relativas entre vários elos (ou entre todos)
•A matriz i −1 A i representa a posição e orientação relativa
entre os sistemas associados a dois elos sucessivos
A representação total do sistema que serve de exemplo:
0
A 2 = 0 A1 1 A 2
Esta abordagem é sistemática

16. Cinemática inversa (1/9)
A cinemática inversa procura determinar os valores das
coordenadas articulares se conhecida a localização do
extremo do membro.
Assim como no caso da cinemática direta, pode-se aplicar
métodos geométricos:
x = r cos θ 
 ⇒ θ = atan2( y , x ), r = x + y
2 2
y = r sen θ
Para casos mais complexos, resulta muito difícil aplicar
este método.

17. Cinemática inversa (2/9)
Da cinemática direta temos:
  
X = f (q ) = T (q ) x
onde q é o vetor das coordenadas articulares:
q = (r1, θ1,, rn , θn )
O problema dacinemática inversa consiste em encontrar
a “inversa” da f tal que
 −1 
q = f (X)

Devido aos senos & cosenos das rotações, f é não linear
em q. Por isso, sua inversa pode não existir ou não ser
uma função elementar (arctan, cos,…).

18. Cinemática inversa (3/9)
A idéia é utilizar uma aproximação linear da função e
achar sua “inversa”:
 
f (q ) = f (q0 ) + J (q0 )(q − q0 ) (Taylor)
onde J (q0 ) é o jacobiano da função no ponto q0 e a
aproximação anterior é válida perto desse ponto.
y
Aproximada
Exata
x

19. Cinemática inversa (4/9)
Cálculo do jacobiano:
Precisamos calcular o jacobiano e logo “invertê-lo”. 
As
colunas do jacobiano são as derivadas parciais de f no
ponto q0. Como da representação de D-H temos
 
f (q ) = R1T1 RnTn x
onde só Ri depende de θ i e só Ti depende de ri ,
pela regra do produto as derivadas parciais são
calculadas como sendo:
 
∂ θ f (q ) = R1T1 Ri
i
′Ti  RnTn x,
 
∂ r f (q ) = R1T1  RiTi ′RnTn x.
i
Por isso é necessário derivar matrizes de rotação e
translação.

20. Cinemática inversa (5/9)
Cálculo do jacobiano:
Derivada de uma matriz de rotação R:
RR T = 1 ⇒ R ′ R T + R(R ′)T = 0 ⇒ R ′ R T = −(R ′ R T )T
Então a velocidade angular Ω = R ′ R T é uma matriz
antissimétrica, que está relacionada com o eixo de rotação

ω = ( ω x , ω y , ωz )
via
 0 − ωz ω y 0 
 ω 0 − ωx 0
Ω= z 
 − ωy ωx 0 0
 0 0 0 0
 
Finalmente, R ′ = R ′R T R = ΩR.

21. Cinemática inversa (6/9)
Cálculo do jacobiano:
Derivada de uma matriz de translação T:
Por exemplo:
1 0 0 0 0 0 0 0
0 1 0 r 0 0 0 1
T =  ⇒ T′ =  
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
   

22. Cinemática inversa (7/9)
Cálculo do jacobiano:
Retomando nosso exemplo, se
 x  c θ1 − s θ1 0 1 0 r1  c θ2 − s θ2 0  1 0 r2  0
 y  = s θ c θ1 0 0 1 0  s θ2 c θ2 0 0 1 0  0
   1     
 1  0
   0 1 0 0 1  0
  0 1 0 0 1  1
  
então o jacobiano resulta ser:
c θ1 − r2 s(θ1 + θ2 ) − r1 s θ1 c(θ1 + θ2 ) − r2 s(θ1 + θ2 )
J = s θ1 r2 c(θ1 + θ2 ) + r1 c θ1 s(θ1 + θ2 ) r2 c(θ1 + θ2 ) 
 
 0
 0 0 0 

O vetor das coordenadas articulares é
q = (r1, θ1, r2 , θ2 )

23. Cinemática inversa (8/9)
Inversa generalizada:
A inversa do jacobiano é tal que, dada uma pequena
variação da posição do extremo, é possível calcular a
variação nas coordenadas articulares:
∆q = J −1 ∆x
Em geral, não existe a inversa do jacobiano, mas sim uma
inversa generalizada B, que cumpre alguma das
condições de Moore-Penrose:
1. JBJ = J 2. BJB = B
3. (JB )T = JB 4. (BJ )T = BJ
Se B cumpre todas as quatro condições, é dita pseudo-
inversa, e é única: B = J +
Achar a inversa generalizada é um processo lento e que
não lida adequadamente com singularidades.

24. Cinemática inversa (9/9)
Transposta do jacobiano:
Em lugar de utilizar a pseudo-inversa do jacobiano, pode-se
utilizar a transposta:
∆q = J T ∆x
É muito mais barato e ainda por cima evita problemas com
singularidades.
Esta aproximação é motivada por considerações físicas
(“trabalho virtual”).
Para resolver certos problemas de escala, pode-se
introduzir um fator de escala h, e iterar até atingir a
convergência:
∆q ( i +1) = h J T ∆x ( i )

25. Referências
Cinemática Inversa:
•Fast Numerical Methods for Inverse Kinematics, Bill Baxter
•Cinemática del robot, Amador
Matrizes em geral:
•Matrix Computations, Gene H. Golub & Charles F. Van Loan