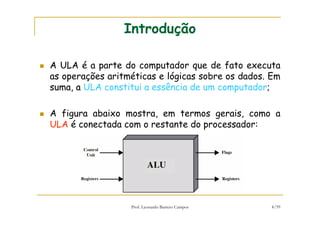
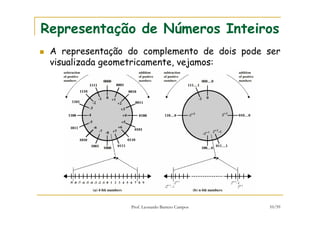
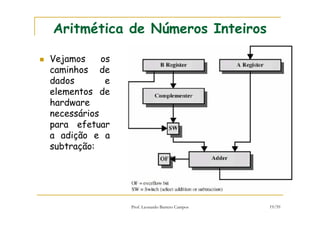
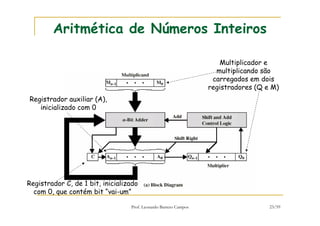
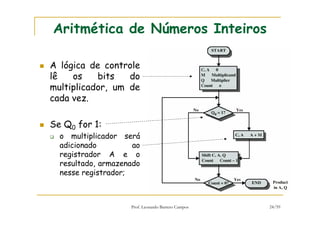
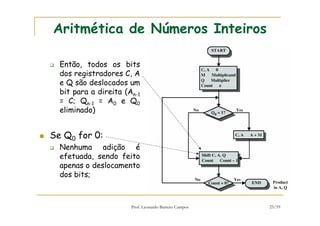
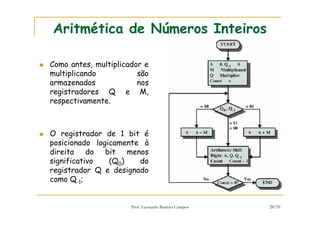
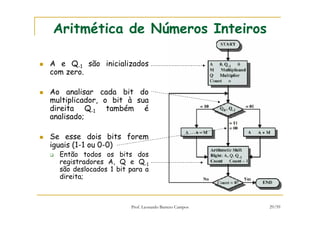
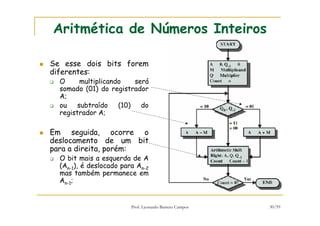
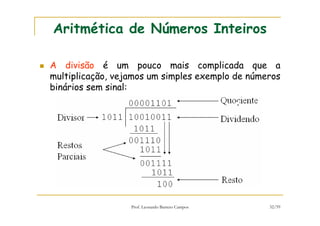
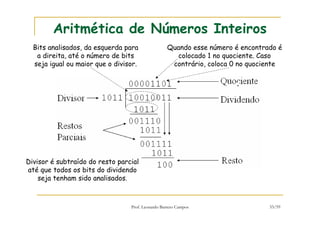
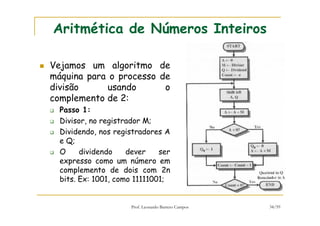
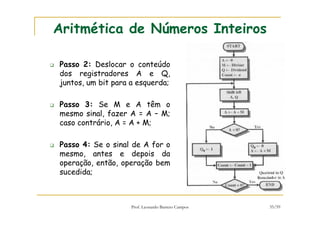
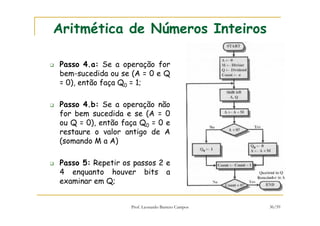
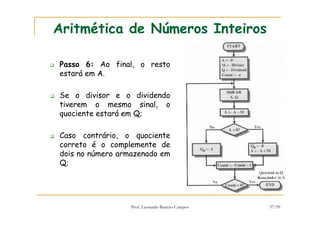
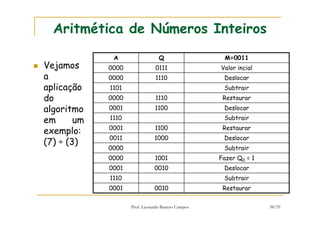
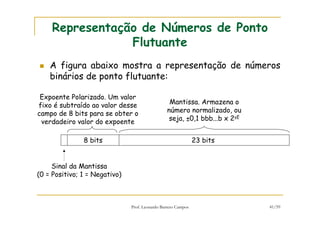
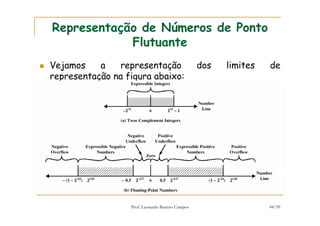
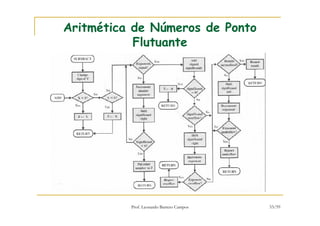
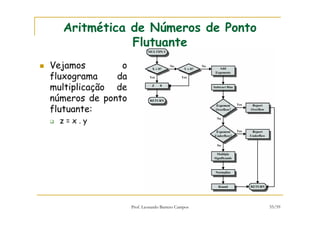
[1] O documento discute representação e aritmética de números inteiros no hardware de um computador, incluindo representação em complemento de dois, operações aritméticas como adição, subtração, multiplicação e divisão. [2] É explicado como esses cálculos são implementados no hardware da unidade lógica e aritmética de um processador. [3] Algoritmos específicos como o algoritmo de Booth para multiplicação com sinal também são apresentados.