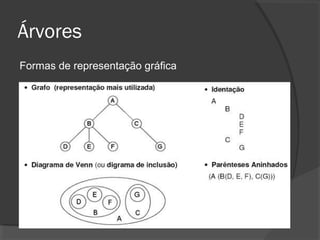
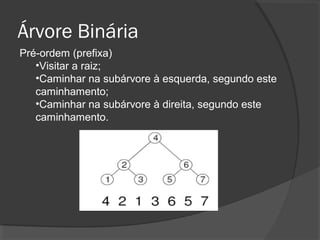
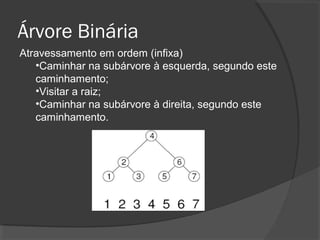
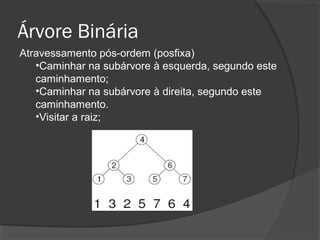
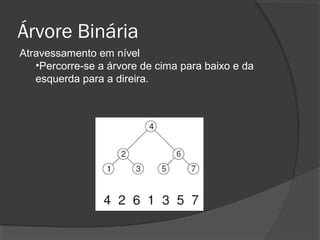
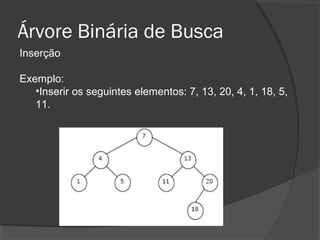
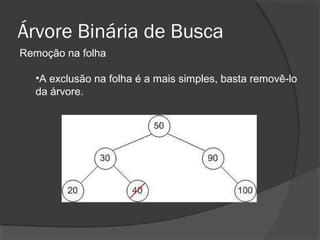
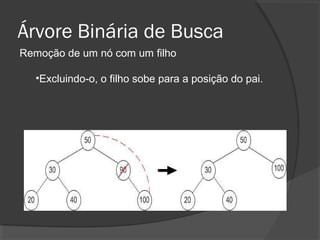
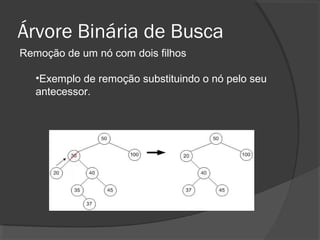
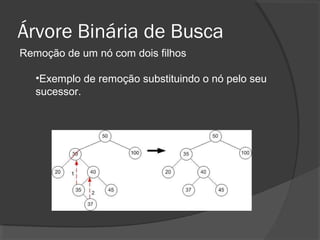
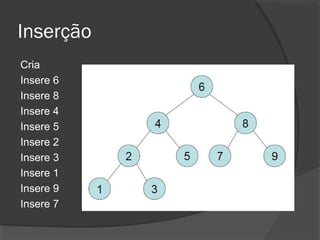
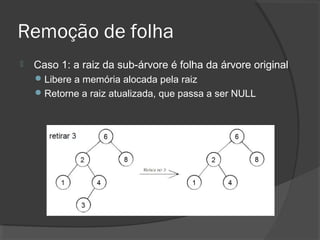
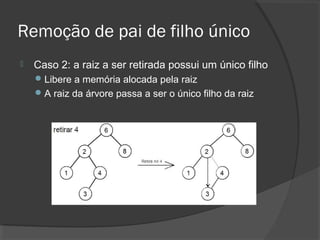
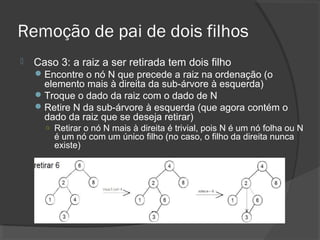
O documento descreve árvores binárias, estruturas de dados hierárquicas onde cada nó tem no máximo dois filhos. Explica que uma árvore binária possui uma raiz e nós internos com duas subárvores esquerda e direita, além de nós folha sem filhos. Também apresenta operações básicas como busca, inserção e remoção em árvores binárias de busca, onde os nós são ordenados.

1. Arvore Binária

2. Árvores

São estruturas de dados
representação de hierarquias.
adequadas
para
a

Uma árvore é composta por um conjunto de nós.

Existe um nó r, denominado raiz, que contém zero ou
mais subárvore, cujas raízes são ligadas diretamente a
r.

A raiz se liga a um ou mais elementos, e cada um
destes forma uma nova subárvore. Esses elementos
são seus galhos ou filhos.

3. Árvores
Fundamentos básicos
GRAU – número de subárvore de um nó.
FOLHA – um nó que possui grau zero, ou seja, não
possui subárvore.
FILHOS – são as raízes das subárvore de um nó.
Nó não terminal é um nó que não é uma folha e é
diferente da raiz.

4. Árvores
Fundamentos básicos
A altura de uma árvore é o comprimento do caminho
mais longo da raiz até uma das folhas.
Uma árvore nula tem altura 0.
Todos os nós são acessíveis a partir da raiz.
Existe um único caminho entre a raiz e qualquer
outro nó.

5. Árvores
Formas de representação gráfica

6. Árvore Binária
Árvore Binária: Uma árvore binária é uma árvore
que pode ser nula, ou então tem as seguintes
características:
Existe um nó especial denominado raiz;
Nenhum nó tem grau superior a 2 (dois), isto é,
nenhum nó tem mais de dois filhos;
Existe um “senso de posição”, ou seja, distinguese entre uma subárvore esquerda e uma
subárvore direita.

7. Árvore Binária
Atravessamento (ou caminhamento) de árvore é a
passagem de forma sistemática por cada um de seus
nós;
Diferentes formas de percorrer os nós de uma árvore:
Pré-ordem ou prefixa (busca em profundidade)
Em ordem ou infixa (ordem central)
Pós-ordem ou posfixa
Em nível

8. Árvore Binária
Pré-ordem (prefixa)
•Visitar a raiz;
•Caminhar na subárvore à esquerda, segundo este
caminhamento;
•Caminhar na subárvore à direita, segundo este
caminhamento.

9. Árvore Binária
Atravessamento em ordem (infixa)
•Caminhar na subárvore à esquerda, segundo este
caminhamento;
•Visitar a raiz;
•Caminhar na subárvore à direita, segundo este
caminhamento.

10. Árvore Binária
Atravessamento pós-ordem (posfixa)
•Caminhar na subárvore à esquerda, segundo este
caminhamento;
•Caminhar na subárvore à direita, segundo este
caminhamento.
•Visitar a raiz;

11. Árvore Binária
Atravessamento em nível
•Percorre-se a árvore de cima para baixo e da
esquerda para a direira.

12. Árvore Binária
Árvore Estritamente Binária:
•É uma árvore binária na qual todo nó tem 0 ou 2
subárvore, ou seja, nenhum nó tem “filho único”.

13. Árvore Binária
Árvore Binária Cheia
•Todos os nós, exceto os do último nível, possuem
exatamente duas subárvore.
•Uma árvore binária cheia de altura h tem 2h – 1 nós.

14. Árvore Binária
Árvore Degenerada
•Cada nó possui exatamente um filho, e a árvore tem o
mesmo número de níveis que de nós.

15. Árvore Binária de Busca

Uma árvore é denominada árvore binária de busca
se:
Todo elemento da subárvore esquerda é menor que
o elemento raiz;
Nenhum elemento da subárvore direita é menor que
o elemento raiz;
As subárvore direita e esquerda também são árvores
de busca binária;

16. Árvore Binária de Busca

Busca
Se o valor for igual à raiz, o valor existe na árvore.
Se o valor for menor do que a raiz, então deve
buscar-se na subárvore da esquerda, e assim
recursivamente, em todos os nós da subárvore.
Se o valor for maior que a raiz, deve-se buscar na
subárvore da direita, até alcançar-se o nó folha da
árvore, encontrando ou não o valor requerido.

17. Árvore Binária de Busca

Inserção
Se a árvore estiver vazia, cria um novo nó e insere as
informações do novo nó.
Compara a chave a ser inserida com a chave do nó
analisado:
Se menor, insere a chave na subárvore esquerda;
Se maior, insere a chave na subárvore direita.

18. Árvore Binária de Busca
Inserção
Exemplo:
•Inserir os seguintes elementos: 7, 13, 20, 4, 1, 18, 5,
11.

19. Árvore Binária de Busca

Remoção
A remoção de um nó é um processo mais complexo.
Para excluir um nó de uma árvore binária de busca, há
de se considerar três casos distintos:
o Remoção na folha;
o Remoção de um nó com um filho;
o Remoção de um nó com dois filhos.

20. Árvore Binária de Busca
Remoção na folha
•A exclusão na folha é a mais simples, basta removê-lo
da árvore.

21. Árvore Binária de Busca
Remoção de um nó com um filho
•Excluindo-o, o filho sobe para a posição do pai.

22. Árvore Binária de Busca
Remoção de um nó com dois filhos
•Neste caso, pode-se operar de duas maneiras
diferentes:
•Substitui-se o valor do nó a ser retirado pelo valor
sucessor (o nó mais à esquerda da subárvore
direita);
•Substitui-se o valor do nó a ser retirado pelo valor
antecessor (o nó mais à direita da subárvore
esquerda).

23. Árvore Binária de Busca
Remoção de um nó com dois filhos
•Exemplo de remoção substituindo o nó pelo seu
antecessor.

24. Árvore Binária de Busca
Remoção de um nó com dois filhos
•Exemplo de remoção substituindo o nó pelo seu
sucessor.

25. Tipo Árvore Binária de Busca

Árvore é representada pelo ponteiro para o nó raiz.
struct noArv {
int info;
struct noArv* esq;
struct noArv* dir;
};
typedef struct noArv NoArv;

26. Criação

Árvore vazia representada por NULL:
NoArv* abb_cria(void){
return NULL;
}

27. Impressão

Imprime os valores da árvore em ordem crescente,
percorrendo os nós em ordem simétrica:
void abb_imprime (NoArv* a){
if (a != NULL) {
abb_imprime(a -> esq);
printf(“%dn”,a -> info);
abb_imprime(a ->dir);
}
}

28. Busca


Explora a propriedade de ordenação da árvore;
Possui desempenho computacional proporcional à
altura.
NoArv* abb_busca (NoArv* r, int v){
if (r == NULL)
return NULL;
else if (r -> info > v)
return abb_busca (r -> esq, v);
else if (r -> info < v)
return abb_busca (r -> dir, v);
else return r;
}

29. Inserção



Recebe um valor v a ser inserido
Retorna o eventual novo nó raiz da (sub-) árvore
Para adicionar v na posição correta, faça:
 Se a (sub-) árvore for vazia
○ Crie uma árvore cuja raiz contém v
 Se a (sub-) árvore não for vazia
○ Compare v com o valor na raiz
○ Insira v na subárvore esquerda ou na subárvore direita,
conforme o resultado da comparação.

30. Exemplo Inserção
NoArv* abb_insere (NoArv* a, int v){
if (a == NULL) {
a = (NoArv*) malloc(sizeof(NoArv));
é necessário atualizar os ponteiros para
a -> info = v;
as sub-árvores à esquerda ou à direita
quando da chamada recursiva da função,
a -> esq = a -> dir = NULL;
pois a função de inserção pode alterar
o valor do ponteiro para a raiz da (sub-)árvore .
}
else if (v < a -> info)
a -> esq = abb_insere(a -> esq, v);
else /* v >= a -> info */
a -> dir = abb_insere (a -> dir, v);
return a;
}

31. Inserção
Cria
Insere 6
Insere 8
Insere 4
Insere 5
Insere 2
Insere 3
Insere 1
Insere 9
Insere 7

32. Remoção



Recebe um valor v a ser inserido
Retorna a eventual nova raiz da árvore
Para remover v, faça:
 Se a árvore for vazia
○ Nada tem que ser feito
 Se a árvore não for vazia
○ Compare o valor armazenado no nó raiz com v
○ Se for maior que v, retire o elemento da sub-árvore à esquerda
○ Se for menor que v, retire o elemento da sub-árvore à direita
○ Se for igual a v, retire a raiz da árvore

33. Remoção

Para retirar a raiz da árvore, há 3 casos:
 Caso 1: a raiz que é folha
 Caso 2: a raiz a ser retirada possui um único filho
 Caso 3: a raiz a ser retirada tem dois filhos.

34. Remoção de folha

Caso 1: a raiz da sub-árvore é folha da árvore original
 Libere a memória alocada pela raiz
 Retorne a raiz atualizada, que passa a ser NULL

35. Remoção de pai de filho único

Caso 2: a raiz a ser retirada possui um único filho
 Libere a memória alocada pela raiz
 A raiz da árvore passa a ser o único filho da raiz

36. Remoção de pai de dois filhos

Caso 3: a raiz a ser retirada tem dois filho
 Encontre o nó N que precede a raiz na ordenação (o
elemento mais à direita da sub-árvore à esquerda)
 Troque o dado da raiz com o dado de N
 Retire N da sub-árvore à esquerda (que agora contém o
dado da raiz que se deseja retirar)
○ Retirar o nó N mais à direita é trivial, pois N é um nó folha ou N
é um nó com um único filho (no caso, o filho da direita nunca
existe)

37. NoArv* abb_retira (NoArv* r, int v) {
if (r == NULL)
return NULL;
else if (r -> info > v)
r->esq = abb_retira (r -> esq, v);
else if (r->info < v)
r->dir = abb_retira(r->dir, v);
else { /* achou o nó a remover */
/* nó sem filhos */
if (r->esq == NULL && r->dir == NULL) {
free (r);
r = NULL;
}
/* nó só tem filho à direita */
else if (r->esq == NULL) {
NoArv* t = r;
r = r->dir;
free (t);
}

38. /* só tem filho à esquerda */
else if (r->dir == NULL) {
NoArv* t = r;
r = r->esq;
free (t);
}
/* nó tem os dois filhos */
else {
NoArv* f = r->esq;
while (f->dir != NULL) {
f = f->dir;
}
r->info = f->info; /* troca as informações */
f->info = v;
r->esq = abb_retira(r->esq,v);
}
}
return r;
}

39. “As árvores da computação têm a tendência de
crescer para baixo: a raiz fica no ar enquanto as
folhas se enterram no chão."