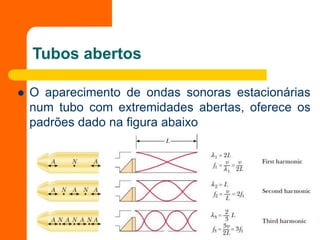
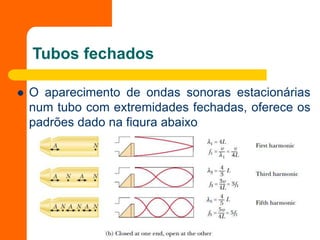
O documento discute conceitos fundamentais de acústica, como propagação do som, frequência, altura, velocidade, intensidade, timbre e ressonância. Explica como ondas sonoras se comportam em tubos abertos e fechados, gerando padrões de ondas estacionárias em frequências de ressonância. Também aborda o efeito Doppler e velocidade supersônica.

1. Acústica

2. Som
 Usando uma definição geral, ondas sonoras são
ondas mecânicas longitudinais que podem se
propagar através de gases, líquidos ou sólidos.
 Como toda onda, o som tem Amplitude,
Comprimento de Onda, Freqüência, Período, se
propaga com uma certa velocidade (que depende
do meio em que se propaga).
 Através desses elementos, podemos observar
certos fenômenos:

3. Freqüência
 Os sons audíveis pelo ouvido humano têm uma
freqüência entre 20 Hz e 20000 Hz. Acima e
abaixo desta faixa estão ultra-som e infra-som,
respectivamente.
 Ultra-som → é onda mecânica, longitudinal e de
freqüência superior a 20000 Hz.
 Infra-som → é a onda mecânica, longitudinal e de
freqüência inferior a 20 Hz.

4. Altura
 A freqüência está relacionada com o conceito de
agudo e grave.
 Uma onda sonora aguda é uma onda em que a
freqüência é alta.
 Uma onda sonora grave é uma onda em que a
freqüência é baixa.

5. Velocidade
 A velocidade do som no ar é de
aproximadamente 340 m/s. Essa velocidade
aumenta quando o som se propaga em meios
mais densos, como nos líquidos e sólidos.
 Assim como uma onda qualquer, o som vai
obedecer a equação da velocidade de uma
onda:
f
v 
 

6. Intensidade Sonora
 A intensidade da onda está
associada à sua amplitude. Quanto
maior for sua amplitude maior será
sua intensidade.
 A intensidade a onda é definida pela
razão entre a potência da fonte e a
unidade de área:
 A unidade de medida da intensidade
sonora é dada pela razão da unidade
de medida de potência (Watt) e a
unidade de media da área (metro
quadrado): W/m2.
A
P
I 

7. Timbre
 Em música, chama-se timbre à característica
sonora que nos permite distinguir se sons de
mesma freqüência foram produzidos por fontes
sonoras conhecidas e que nos permite diferenciá-
las.
 O Lá central do piano, por exemplo, possui a
freqüência de 440Hz. A mesma nota produzida
por um violino possui a mesma freqüência. O que
permite ao ouvido diferenciar os dois sons e
identificar sua fonte é a forma da onda e seu
envelope sonoro, ou seja, seu timbre.

8. Ressonância
 A Ressonância
Acústica é gerada
quando uma fonte
emite um som de
freqüência igual à
freqüência de
vibração natural de
um receptor.

9. Ressonância
 Cada elemento ou parte de um corpo, tem uma “Freqüência
Natural” ou uma freqüência na qual ele “gosta” de vibrar.
 Tocar um sino ou tanger a corda de um violão faz com que eles
vibrem em sua freqüência natural.
 A freqüência natural de cada objeto é determinada por sua massa
e rigidez.
 Aumentar a massa (ou peso) de um objeto reduz ou abaixa a sua
freqüência natural. Aumentar a rigidez do objeto, como por
exemplo aumentar a tração de uma corda do violão, aumenta ou
sobe sua freqüência natural.
 O fato de que cada objeto tem pelo menos uma freqüência natural
não implica em um problema. Mas, um problema de vibração
excessiva pode acontecer como resultado da coincidência de uma
freqüência natural do corpo com uma freqüência inerente de
funcionamento dela.

10. Ressonância

11. Ondas Estacionárias
 Onda estacionária é aquela obtida pela interferência de
duas ondas iguais propagando-se em um mesmo meio
mas em sentido contrário.
 A onda estacionária têm pontos que vibram mais e pontos
que não vibram.
 Os pontos de maior amplitude de vibração são
denominados Antinós ou Ventres.
 Os pontos de amplitude zero, são denominados Nós.
 A distância entre dois nós consecutivos ou dois ventres
consecutivos é a metade de um comprimento de onda λ/2

12. Ondas Estacionárias
 Ondas estacionárias podem ser gerados ao se vibrar uma
ponta da corda esticada em diferentes freqüências,
enquanto a outra ponta está fixa.
 Observe os nós e os antinós. Os modos de oscilação
ocorrem somente em freqüências discretas bem definidas.
Dizemos que o sistema entra em ressonância nessas
freqüências.
 Se a corda é vibrada em alguma outra freqüência diferente
das freqüências de ressonância, uma onda estacionária
não é gerada e as oscilações na corda não aparece, assim
as oscilações na corda são de amplitudes pequenas.

13. Ondas Estacionárias
 Considere que a figura acima seja uma corda de
violão, que está esticada entre dois grampos
separados de uma distância fixa L, e faz-se a
corda oscilar numa freqüência de ressonância,
gerando-se uma onda estacionária.
 Aqui existe um antinó no centro da corda e a
distância L é igual a (λ/2), onde λ é o comprimento
de onda necessário para gerar este padrão de
onda estacionária.

14. Ondas Estacionárias
 Ao vibrar, a corda pode emitir um conjunto de
freqüências denominada Harmônicos.
 O padrão mostrado na figura corresponde ao 1°
Harmônico.
 Os Harmônicos mostram como a onda
estacionária vai se comportar quando
aumentarmos a tenção ou a massa da corda.

15. Harmônicos
 1° Harmônico
 2° Harmônico
 3°Harmônico

1
2
1 


2
1
1
1
v
v
f 



2
2
2 


2
2
2
2
v
v
f 



3
2
3 


2
3
3
3
v
v
f 



16. Harmônicos
 O número de ventres é igual ao número do
harmônico emitido pela corda.
 Assim generalizamos:
 Onde n = 1; 2; 3; 4....

n
n
2

 1
2
f
n
nv
v
f
n
n 






17. Harmônicos
 O aparecimento de uma onda estacionária é devido à
reflexão da ondas nas extremidades fixas da corda. Se
existe uma relação apropriada entre o comprimento do fio
e o das ondas , a superposição destas, propagando-se em
sentidos opostos, produz um padrão de onda estacionária
(ou modo de oscilação).
 O comprimento de onda necessário para que isto aconteça
é o correspondente a uma das freqüências de ressonância
da corda.
 Assim podemos gerar ondas sonoras estacionárias num
tubo de maneira semelhante.

18. Tubos sonoros
 Quando ondas sonoras se propagam através do
ar num tubo, são refletidas em ambas as suas
extremidades.
 Esta reflexão ocorre mesmo quando uma
extremidade esteja aberta.
 Existindo uma relação entre o comprimento de
onda da onda sonora e o comprimento do tubo, a
superposição das ondas propagando-se em
sentidos contrários, irá caudas o aparecimento de
uma padrão de onda estacionária

19. Tubos abertos
 O aparecimento de ondas sonoras estacionárias
num tubo com extremidades abertas, oferece os
padrões dado na figura abaixo

20. Tubos abertos
 De um modo geral, as freqüências de ressonância
para um tubo de comprimento L, com ambas as
extremidades abertas, correspondem aos
comprimentos de onda:
 Onde n é chamado de número harmônico. Logo a
freqüência ressonantes são:

n
n
2


1
2
f
n
nv
v
f
n
n 






21. Tubos fechados
 O aparecimento de ondas sonoras estacionárias
num tubo com extremidades fechadas, oferece os
padrões dado na figura abaixo

22. Tubos fechados
 De um modo geral, as freqüências de ressonância
para um tubo de comprimento L, com somente
uma das extremidades abertas, correspondem aos
comprimentos de onda:
 Onde n é chamado de número harmônico e
sempre impar. Logo a freqüência ressonantes são:

n
n
4



4
nv
v
f
n
n 



23. Efeito Doppler
 Existe uma relação que possibilita calcular a freqüência
percebida por um observador quando houver movimento
relativo entre observador e fonte. Essa relação ficou
conhecida como efeito Doppler
 Para descobrir os sinais das velocidades, basta construir
um eixo orientado do observador para a fonte.
fonte
som
observador
som
v
v
v
v
f
f



'

24. Velocidade Supersônica
 Se uma fonte se aproxima de um detector
estacionário a uma velocidade igual à do som, isto
é, se vfonte a equação prevê que a freqüência f’
será infinita. Isso significa que a fonte se move tão
rápido, que alcança suas próprias frentes de onda.
Avião quebrando a barreira do som