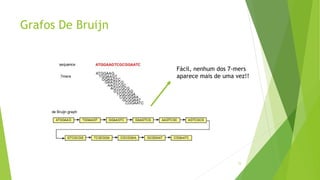
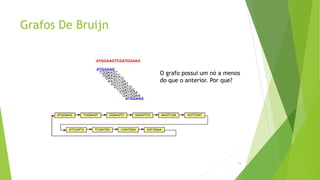
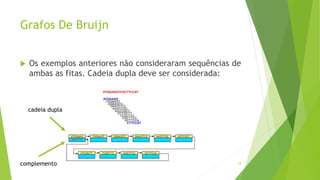
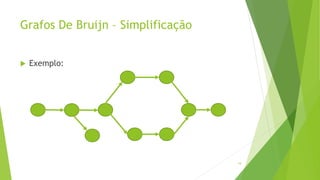
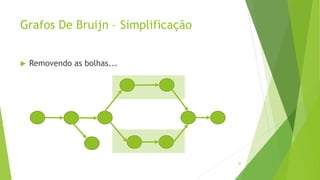
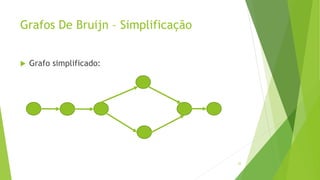
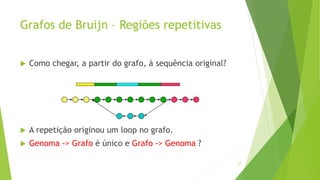
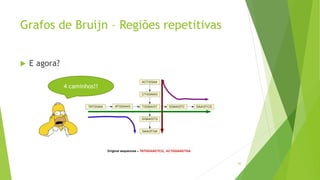
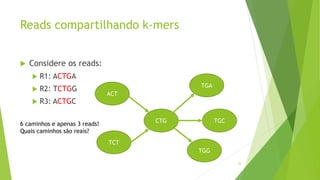
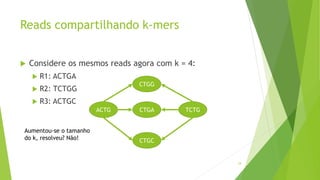
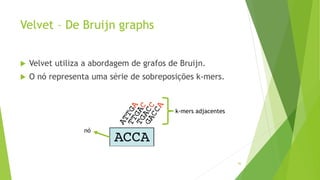
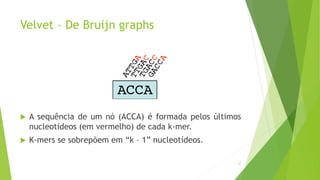
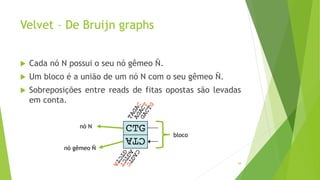
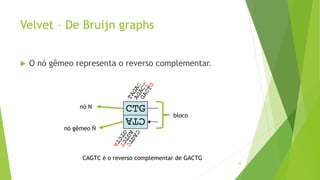
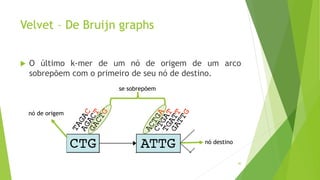
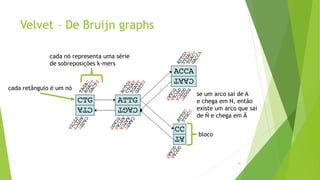
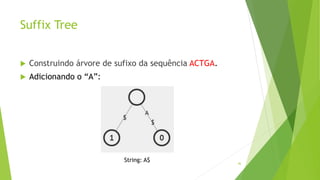
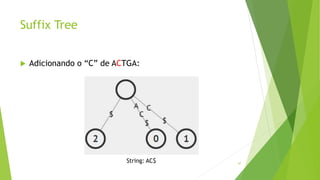
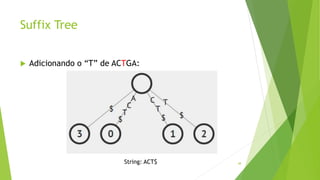
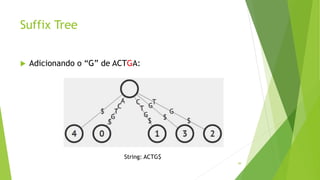
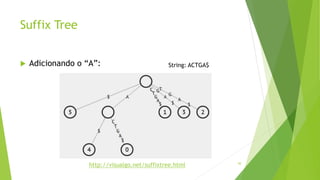
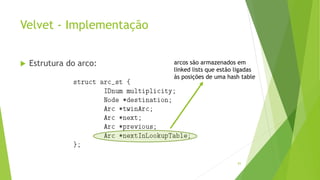
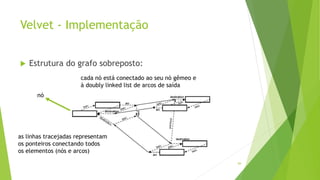
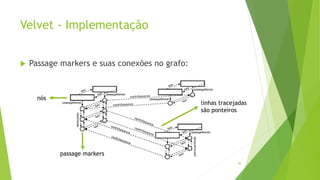
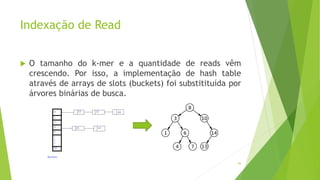
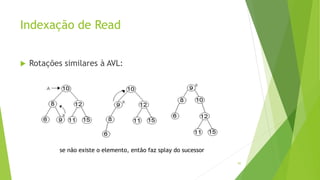
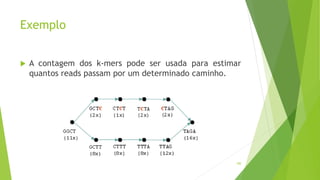
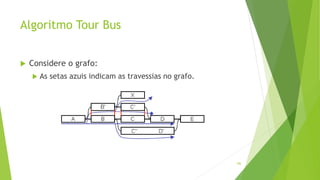
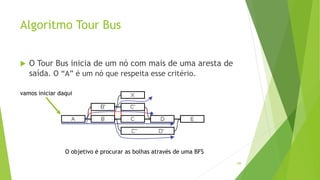
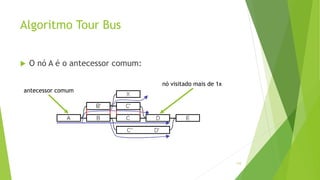
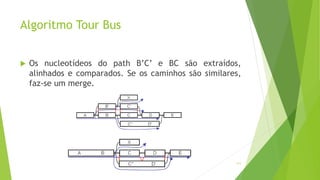
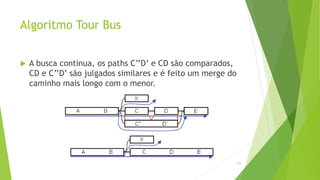
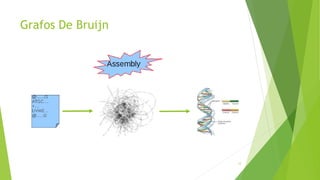
Velvet é um assembler gratuito em C projetado para montar short reads produzidos por tecnologias de sequenciamento de nova geração. Ele utiliza um grafo de Bruijn para representar os dados, no qual cada nó representa uma série de k-mers sobrepostos. Velvet simplifica o grafo removendo nós desnecessários e utiliza propriedades dos caminhos no grafo para montar contigs a partir das sequências originais.

1. VELVET ASSEMBLER
Marcos Castro
Grupo de Bioinformática - Unifesp

2. Velvet assembler
 Velvet é um assembler para short reads.
 Criador: Daniel Zerbino.
 http://www.ebi.ac.uk/~zerbino/velvet/
 Uma “short interview” com Zerbino:
 https://www.biostars.org/p/117134/
 Velvet foi feito em linguagem C e é gratuito (GPL).
 Há rumores que foi feito utilizando o editor Vim!
2

3. Motivação
 Apesar do sequenciamento do genoma humano, a
maioria das espécies ainda não foram sequenciadas!
 A montagem de shotgun reads é um desafio no
sequenciamento do genoma de novo.
 De novo: sem genoma de referência.
 Objetivo da montagem:
 Reunir os fragmentos extraídos (shotgun reads) para
formar um conjunto de sequências contíguas (contigs).
3

4. Tecnologias NGS
 Novos métodos de sequenciamento têm surgido.
 Exemplo: Illumina, SOLiD.
 Tecnologias NGS produzem reads bem menores do que o
tradicional método de Sanger.
 Sanger: em torno de 400-500 bp
 Illumina: 50 bp
4

5. Tecnologias NGS
 Geração de uma grande quantidade de dados.
 Fragmentos produzidos muito pequenos (short reads).
 Vantagens:
 Rapidez, custo.
 Requer menos amostra de DNA.
 Desvantagem:
 Short reads com altas taxas de erro.
5

6. Tecnologias NGS
6

7. Assembly
 Após a produção dos reads, é preciso montá-los.
 Existem várias ferramentas de montagem (assemblers).
 Várias dessas ferramentas utilizam a abordagem OLC
(overlap-layout-consensus).
7

8. Assembly
 Na OLC, alinham-se os fragmentos dois a dois para
encontrar quais pares de reads possuem uma
sobreposição (overlap) consistente.
 Analogia: procurar por peças de um quebra-cabeça que
se encaixam e que possuem cores correspondentes.
 Dificuldade: distinguir sobreposições inexatas.
 Erros de sequenciamento.
 Regiões de similaridade (highly conserved repeats).
8

9. Assembly
 O assembler detecta clusters de reads, formando os
contigs.
 Analogia: partes da imagem colocadas juntas em um
quebra-cabeça.
 Partes ambíguas:
9

10. Assembly
 O assembler tenta ordenar e orientar os contigs.
 A informação paired-end pode ser usada pelo assembler
para estimar a distância que separam os contigs.
 Conjuntos de contigs que podem ser colocados na
mesma região são chamados de supercontigs (scaffolds).
 Ao final da montagem, um conjunto de scaffolds estarão
disponíveis.
10

11. Assembly
 É desejável remover a maior quantidade de gaps
possível.
 Montagens de cromossomos inteiros.
 Pode ser muito custoso.
 Gaps podem ocorrer devido:
 Falta de cobertura.
 Complexidade da sequência.
11

12. Grafos De Bruijn
12

13. Grafos De Bruijn
 Em grafos De Bruijn, os reads são quebrados em
sequências menores (substrings) chamadas k-mers.
 Esse tipo de grafo foi proposto originalmente para
manipular melhor a montagem de regiões repetitivas.
13
Problema?

14. Grafos De Bruijn
 k-mer é uma substring de tamanho k.
 Exemplo de string: GGCGATTCATCG
 Se k = 4, temos os 4-mers: GGCG, GCGA, CGAT ...
 Se k = 3, temos os 3-mers: GGC, GCG, CGA ...
 Como gerar todos os k-mers em Python:
 [s[i:i+k] for i in range(len(s)) if len(s[i:i+k]) == k]
 “s” é a string e “k” é o tamanho da substring.
14

15. Grafos De Bruijn
15
Fácil, nenhum dos 7-mers
aparece mais de uma vez!!

16. Grafos De Bruijn
16
O grafo possui um nó a menos
do que o anterior. Por que?

17. Grafos De Bruijn
 Algoritmo para construção dos grafos De Bruijn:
 1) Quebra os reads em k-mers.
 2) Conecta os k-mers baseados na regra dos “k – 1”
nucleotídeos comuns (sufixo/prefixo).
17

18. Grafos De Bruijn
 Os exemplos anteriores não consideraram sequências de
ambas as fitas. Cadeia dupla deve ser considerada:
18
cadeia dupla
complemento

19. Grafos De Bruijn – Simplificação
 Exemplo:
19

20. Grafos De Bruijn – Simplificação
 Removendo as bolhas...
20

21. Grafos De Bruijn – Simplificação
 Removendo as pontas...
21

22. Grafos De Bruijn – Simplificação
 Grafo simplificado:
22

23. Tamanho do k-mer
 Um k-mer menor:
 Aumenta possibilidade de conectividade (sensibilidade).
 Mais regiões ambíguas (menor especificidade).
 Um k-mer maior:
 Aumenta a especificidade.
 Diminui a conectividade.
23

24. Tamanho do k-mer
 Prefere-se pegar valores de “k” ímpares.
 Exemplo para “k” par: ATATATATATAT
 Complementar reverso: ATATATATATAT
 Exemplo para “k” ímpar: ATATATATATA
 Complementar reverso: TATATATATAT
 Conclusão: com “k” par, alguns k-mers podem ser
complementos reversos de si mesmos! Problema?
24
palíndromos

25. Tamanho do k-mer
 K-mers sendo complemento reverso de si mesmos geram
ambiguidade no grafo tornando a sua resolução mais
difícil.
 Como evitar os k-mers palíndromos?
 Utilizando um “k” ímpar!
 Velvet requer um “k” ímpar.
 Caso você escolha um “k” par, o Velvet decrementa!
25

26. Tamanho do k-mer
 Com k-mers mais longos, fica mais fácil de converter o
grafo de Bruijn em uma única sequência.
 Porém, “k” maiores requerem mais memória para
armazenar e processar o grafo.
 Se possuir RAM “ilimitada”, o tamanho do k-mer pode
ser limitado ao tamanho do short read.
26

27. Grafos de Bruijn – Regiões repetitivas
 Como chegar, a partir do grafo, à sequência original?
 A repetição originou um loop no grafo.
 Genoma -> Grafo é único e Grafo -> Genoma ?
27

28. Grafos de Bruijn – Regiões repetitivas
 Reflexão:
 Se cada k-mer tiver vizinhos únicos, seremos capazes de
construir a sequência?
28

29. Grafos de Bruijn – Regiões repetitivas
29
Muito fácil!!

30. Grafos de Bruijn – Regiões repetitivas
 E agora?
30
4 caminhos!!

31. Reads compartilhando k-mers
 Considere os reads:
 R1: ACTGA
 R2: TCTGG
 R3: ACTGC
 Todos os 3-mers: {ACT, CTG, TGA, TCT, TGG, TGC}
31

32. Reads compartilhando k-mers
 Considere os reads:
 R1: ACTGA
 R2: TCTGG
 R3: ACTGC
32
CTG
TGA
TGG
ACT
TCT
TGC
6 caminhos e apenas 3 reads!
Quais caminhos são reais?

33. Reads compartilhando k-mers
 Considere os mesmos reads, mas com k = 4:
 R1: ACTGA
 R2: TCTGG
 R3: ACTGC
 Todos os 4-mers: {ACTG, CTGA, TCTG, CTGG, CTGC}
33

34. Reads compartilhando k-mers
 Considere os mesmos reads agora com k = 4:
 R1: ACTGA
 R2: TCTGG
 R3: ACTGC
34
ACTG
CTGG
CTGA
CTGC
TCTG
Aumentou-se o tamanho
do k, resolveu? Não!

35. Contigs mais curtos?
 Uma das características dos assemblers que utilizam
DBG (De Bruijn Graphs) é o aparecimento de contigs
mais curtos do que o comprimento do read.
 Por que isso ocorre?
35

36. Velvet – De Bruijn graphs
 Velvet utiliza a abordagem de grafos de Bruijn.
 O nó representa uma série de sobreposições k-mers.
36
k-mers adjacentes
nó

37. Velvet – De Bruijn graphs
 A sequência de um nó (ACCA) é formada pelos últimos
nucleotídeos (em vermelho) de cada k-mer.
 K-mers se sobrepõem em “k – 1” nucleotídeos.
37

38. Velvet – De Bruijn graphs
 Cada nó N possui o seu nó gêmeo Ñ.
 Um bloco é a união de um nó N com o seu gêmeo Ñ.
 Sobreposições entre reads de fitas opostas são levadas
em conta.
38
nó N
nó gêmeo Ñ
bloco

39. Velvet – De Bruijn graphs
 O nó gêmeo representa o reverso complementar.
39
nó N
nó gêmeo Ñ
bloco
CAGTC é o reverso complementar de GACTG

40. Velvet – De Bruijn graphs
 O último k-mer de um nó de origem de um arco
sobrepõem com o primeiro de seu nó de destino.
40
nó de origem
nó destino
se sobrepõem

41. Velvet – De Bruijn graphs
41
cada retângulo é um nó
cada nó representa uma série
de sobreposições k-mers
se um arco sai de A
e chega em N, então
existe um arco que sai
de Ñ e chega em Ã
bloco

42. Velvet – De Bruijn graphs
 Simplificação:
 Se o nó A tem somente um arco de saída para o nó B e se
o nó B tem somente um arco de entrada, faz-se o merge.
42
sem perda de informação

43. Velvet - Propriedades
 Duas sequências sobrepostas são representadas por dois
caminhos que se sobrepõem.
 Exemplo:
 Sequência S1: ACTG (formada pelo caminho C1)
 Sequência S2: CTGA (formada pelo caminho C2)
 C1 e C2 se sobrepõem.
 C1 ∩ C2 = sobreposição de S1 com S2 = CTG
43

44. Velvet - Propriedades
 Considere as strings:
 S2 = ACTG
 S1 = CTG
 Se S1 é substring de S2, então o caminho de S1 é um
sub-caminho de S2.
 Útil para procurar por reads que se sobrepõem através
de repetições.
44

45. Velvet - Propriedades
 O grafo de Bruijn de uma sequência pode ser
considerado como uma simplificação da affix tree dessa
sequência.
 Prefixo: é um afixo que se adiciona à esquerda.
 Exemplo: semicírculo
 Sufixo: é um afixo que se adiciona à direita.
 Exemplo: loteria
 Afixos: prefixos e sufixos.
45

46. Suffix Tree
 Construindo árvore de sufixo da sequência ACTGA.
 Adicionando o “A”:
46
String: A$

47. Suffix Tree
 Adicionando o “C” de ACTGA:
47
String: AC$

48. Suffix Tree
 Adicionando o “T” de ACTGA:
48String: ACT$

49. Suffix Tree
 Adicionando o “G” de ACTGA:
49
String: ACTG$

50. Suffix Tree
 Adicionando o “A”:
50
http://visualgo.net/suffixtree.html
String: ACTGA$

51. Suffix Tree
 Aplicação da Suffix Tree:
 Maior substring comum (longest common substring)
 Hey, cuidado, não é “longest common subsequence”.
 Maior substring comum: contígua.
 Maior subsequência comum: não contígua.
 Suffix Tree é muito utilizada para manipular uma
enorme quantidade de dados (problemas biológicos).
51

52. Suffix Tree
 Uma das formas eficientes de construir uma suffix tree
é utilizando o algoritmo de Ukkonen.
 Complexidade: O(n logn) em geral.
 Dificuldade: implementação.
 Implementação:
 http://www.geeksforgeeks.org/ukkonens-suffix-tree-
construction-part-6/
52

53. Suffix Tree – Links úteis
 http://www.geeksforgeeks.org/ukkonens-suffix-tree-
construction-part-1/ (possui parte 1, 2, 3 até 6)
 https://www.youtube.com/watch?v=aPRqocoBsFQ
 https://www.youtube.com/watch?v=UrmjCSM7wDw
53

54. Suffix Tree
 Para um conjunto de strings/palavras/reads:
 Generalized suffix tree.
 http://www.geeksforgeeks.org/generalized-suffix-tree-1/
54

55. Velvet - Implementação
 Código no GitHub:
 https://github.com/dzerbino/velvet
 Na pasta “src” encontram-se os arquivos de código.
55

56. Velvet - Implementação
 Estrutura do grafo: (arquivo graph.c)
56

57. Velvet - Implementação
 Estrutura do grafo:
57
contador de sequências

58. Velvet - Implementação
 Retorna o número de sequências utilizadas para
construir o grafo:
58

59. Velvet - Implementação
 Estrutura do grafo:
59
contador de nós

60. Velvet - Implementação
 Retorna o número de nós do grafo:
60

61. Velvet - Implementação
 Estrutura do grafo:
61
tamanho do k-mer

62. Velvet - Implementação
62
se quiser alterar, basta recompilar
com um tamanho maior

63. Velvet - Implementação
 Estrutura do grafo:
63
O grafo armazena ponteiros
para todos os nós.

64. Velvet - Implementação
 Exemplo para destruir um nó:
64

65. Velvet - Implementação
 Estrutura do grafo:
65
array de arrays de marcadores
short reads agrupados por nó

66. Velvet - Implementação
 Estrutura do grafo:
66
tamanhos dos nodeReads

67. Velvet - Implementação
 Estrutura do grafo:
67
ponteiros para gap markers
??

68. Velvet - Implementação
 Estrutura do nó:
68
identificação do nó

69. Velvet - Implementação
 Estrutura do nó:
69
cada nó tem um ponteiro
para o seu nó gêmeo, cujo ID
é o ID do nó multiplicado por -1

70. Velvet - Implementação
 Estrutura do nó:
70
corresponde ao nucleotídeos finais
dos k-mers representados por esse nó
se s(n) é a sequência do nó,
o tamanho do nó é length(s(n))

71. Velvet - Implementação
71

72. Velvet - Implementação
 Cada nó está ligado a uma lista duplamente encadeada
de arcos de saída.
 Por causa da simetria do grafo, todos os arcos de
entrada têm correspondência com um arco de saída do
nó gêmeo.
 Por isso, somente ponteiros para arcos de saída são
armazenados (economia de memória).
72

73. Velvet - Implementação
 Estrutura do nó:
73
número de arcos da lista
duplamente encadeada

74. Velvet - Implementação
 Reads estão associadas aos nós de duas formas:
 Long reads são representadas por objetos PassageMarker
em uma lista ligada cujo primeiro elemento é
armazenado dentro do nó.
 Short reads são representadas por shortReadMarker que
são armazenados em um array ligado ao grafo.
74

75. Velvet - Implementação
 Estrutura do nó:
75
representam long reads

76. Velvet - Implementação
 Estrutura do nó:
76
variáveis booleanas que permitem
acompanhar o progresso dos algoritmos

77. Velvet - Implementação
 Estrutura do arco:
77
arcos são mais simples,
pois bastante informação é
armazenada nos nós

78. Velvet - Implementação
 Estrutura do arco:
78
cada arco possui seu nó de
destino e sua multiplicidade

79. Velvet - Implementação
 Estrutura do arco:
79
quantidade de reads que
passam pelo arco ou pelo
seu reverso complementar

80. Velvet - Implementação
 Estrutura do arco:
80
nó de destino

81. Velvet - Implementação
 Estrutura do arco:
81
o arco gêmeo possui a
mesma multiplicidade

82. Velvet - Implementação
 Estrutura do arco:
82
ponteiros da doubly linked list de
arcos que saem do nó de origem

83. Velvet - Implementação
 Estrutura do arco:
83
arcos são armazenados em
linked lists que estão ligadas
às posições de uma hash table

84. Velvet - Implementação
 Estrutura do grafo sobreposto:
84
nó
as linhas tracejadas representam
os ponteiros conectando todos
os elementos (nós e arcos)
cada nó está conectado ao seu nó gêmeo e
à doubly linked list de arcos de saída

85. Velvet - Implementação
 Estrutura PassageMarker:
85
mapeamento de uma substring
da sequência identificada pelo
sequenceID para o nó

86. Velvet - Implementação
 Estrutura PassageMarker:
86
armazena a coordenada de início
do alinhamento dentro do read e
o término que separa o alinhamento
da extremidade 3’ do nó

87. Velvet - Implementação
 Estrutura PassageMarker:
87
dentro do nó, passage markers são
armazenados como uma doubly linked list

88. Velvet - Implementação
 Estrutura PassageMarker:
88
dentro da sequência, passage markers
são armazenados como uma linked list

89. Velvet - Implementação
 Estrutura PassageMarker:
89
cada passage marker está
ligado a uma estrutura twin
marker que corresponde ao
reverso complementar da
sequência, mapeado para o
nó gêmeo
visitou o passage marker?

90. Velvet - Implementação
 Passage markers e suas conexões no grafo:
90
passage markers
nós
linhas tracejadas
são ponteiros

91. Velvet - Implementação
 Estrutura do ShortReadMarker:
 Numerosos, portanto, estruturas “leves”, associado a
um nó.
91

92. Velvet - Implementação
 Estrutura do ShortReadMarker:
92
ID da sequência

93. Velvet - Implementação
 Estrutura do ShortReadMarker:
93
posição do marcador
no nó (varia bastante)

94. Velvet - Implementação
 Estrutura do ShortReadMarker:
94
deslocamento do marcador
desde o início do read,
normalmente é 0
essa estrutura não é duplicada no nó gêmeo
(economia de memória)

95. Indexação de Read
 O tamanho do k-mer e a quantidade de reads vêm
crescendo. Por isso, a implementação de hash table
através de arrays de slots (buckets) foi substitituída por
árvores binárias de busca.
95

96. Indexação de Read
 Utilização de splay trees.
 Splay: trazer um elemento X para a raiz da árvore
fazendo rotações.
 Objetivo: minimizar o número de acessos para achar a
chave requerida.
 Eficiência através da frequência com que cada nó é
acessado, mantendo estes nós na parte superior da
árvore.
96

97. Indexação de Read
 Rotações similares à AVL:
97
se não existe o elemento, então faz splay do sucessor

98. Indexação de Read
 Por que utilizar splay trees?
 Reduz a complexidade de implementação.
 Embora seja menos eficiente teoricamente, são mais
fáceis de implementar e é na prática tão eficiente quanto
outras formas de binary search trees.
 Embora tenha-se um maior custo de memória, é robusto
para um grande conjunto de dados.
98

99. Indexação de Read
 É feito o hash dos reads de acordo com um tamanho
pré-definido do k-mer.
 A variável “k” é limitada ao tamanho dos reads.
 K-mers menores aumentam a conectividade do grafo.
 Trade-off sensibilidade e especificidade.
99

100. Exemplo
 A contagem dos k-mers pode ser usada para estimar
quantos reads passam por um determinado caminho.
100

101. Velvet – Bolhas (bubbles)
101
 Dois caminhos são considerados redundantes se eles
iniciam e terminam no mesmo nó formando bolhas e
contém sequências similares.
 O que causam caminhos redundantes?
 Erros
 Variantes biológicas tais como SNPs

102. Algoritmo Tour Bus
102
 O Tour Bus algorithm detectar as bolhas.
 O critério para decidir sobre a simplificação pode ser
complexo.
 Um deles: cobertura.

103. Algoritmo Tour Bus
103
 O algoritmo é baseado no Dijkstra (busca em largura).
 O algoritmo inicia de um nó qualquer e percorre o grafo
visitando os nós em ordem crescente de distância do nó
inicial.
 Qual é essa distância?

104. Algoritmo Tour Bus
104
 Qual é essa distância?
 A distância entre nós consecutivos A e B é o tamanho de
s(B) dividido pelo número de reads conectando A à B.

105. Algoritmo Tour Bus
 Se o processo encontrar um nó que já foi visitado, é
realizado um backtrack para descobrir o antecessor
comum dos nós.
 A partir dos caminhos que foram refeitos, é feito um
merge dos dois caminhos.
 O nó que atingiu o nó final primeiro (faster path), é
usado como um consensus por causa da cobertura mais
elevada.
105

106. Algoritmo Tour Bus
106
 Considere o grafo:
 As setas azuis indicam as travessias no grafo.

107. Algoritmo Tour Bus
107
 O Tour Bus inicia de um nó com mais de uma aresta de
saída. O “A” é um nó que respeita esse critério.

108. Algoritmo Tour Bus
108
 O Tour Bus inicia de um nó com mais de uma aresta de
saída. O “A” é um nó que respeita esse critério.
vamos iniciar daqui
O objetivo é procurar as bolhas através de uma BFS

109. Algoritmo Tour Bus
109
 Através dos caminhos B’C’ e BC, o nó D é visitado mais
de uma vez.
nó visitado mais de 1x

110. Algoritmo Tour Bus
110
 O nó A é o antecessor comum:
antecessor comum
nó visitado mais de 1x

111. Algoritmo Tour Bus
111
 Os nucleotídeos do path B’C’ e BC são extraídos,
alinhados e comparados. Se os caminhos são similares,
faz-se um merge.

112. Algoritmo Tour Bus
112
 A busca continua, os paths C’’D’ e CD são comparados,
CD e C’’D’ são julgados similares e é feito um merge do
caminho mais longo com o menor.

113. Algoritmo Tour Bus
 Resumindo:
 Detecta caminhos redundantes. (Dijkstra-BFS)
 Pode-se comparar esses caminhos usando métodos de
programação dinâmica.
 Se forem similares, então faz-se um merge.
113

114. Algoritmo Tour Bus
 Bolhas podem está dentro de outras bolhas que estão
dentro de outras bolhas...
 Como seria o problema de buscar todas as bolhas para
dados reais?
 O problema pode torna-se intratável.
 Pode-se limitar a pesquisa a um limiar threshold.
114

115. Continua...
115

116. Dúvidas?
mcastrosouza@live.com
116

117. Referências
 Zerbino’s original paper:
 http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2336801/
 Velvet Manual:
 http://www.ebi.ac.uk/~zerbino/velvet/Manual.pdf
 De Bruijn Graphs Tutorial:
 http://www.homolog.us/Tutorials/index.php?p=1.1&s=1
117

118. Referências
 Suffix trees, Affix trees and some of their applications
 http://www.techfak.uni-
bielefeld.de/~stoye/dropbox/20060517birkenfeld.pdf
 Suffix trees, Affix trees and some of their applications
 http://www.techfak.uni-
bielefeld.de/~stoye/dropbox/20060517birkenfeld.pdf
118