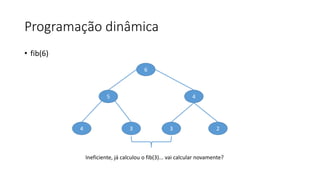
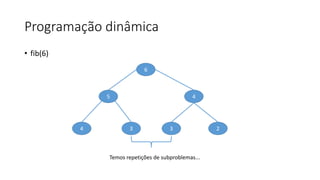
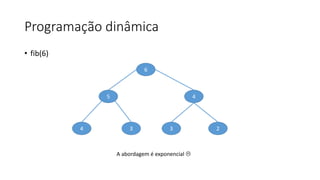
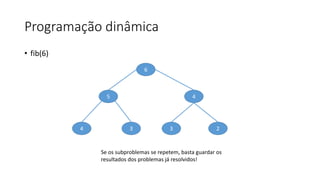
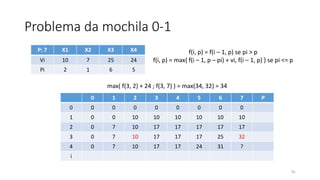
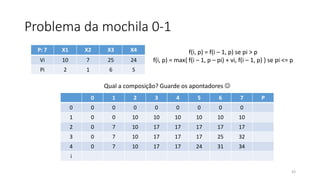
O documento descreve o problema da mochila 0-1, no qual o objetivo é selecionar um conjunto de itens de modo a maximizar o valor total dentro da capacidade máxima de uma mochila. O documento discute abordagens gulosas e de programação dinâmica para resolver o problema, concluindo com uma recorrência recursiva para calcular a solução ótima de forma eficiente.

1. Problema da mochila 0-1
Curso de Maratona de Programação
ICT-Unifesp – SJC

2. Paradigmas
• Guloso
• Realiza a escolha que parece ser a melhor no momento, ou seja, faz uma escolha ótima
local na esperança de que escolha leve até a solução ótima global.
• Será que sempre garante chegar a uma solução ótima global?
• Curiosidade: o algoritmo Dijkstra é guloso... (só guloso ??)

3. Paradigmas
• Backtracking
• Refinamento de busca por força bruta!
• Várias soluções podem ser eliminadas sem serem explicitamente examinadas.

4. Programação dinâmica
• Vários algoritmos eficientes utilizam esse paradigma.
• O termo “programação” significa planejamento.
• Estrutura recursiva:
• A solução de qualquer instância deve conter soluções de subinstâncias da instância.
• Representação por uma recorrência (algoritmo recursivo).
• O algoritmo recursivo é normalmente ineficiente porque refaz cálculos.
• Temos que construir uma tabela para memorizar os resultados de soluções de
subinstâncias (subproblemas) para evitar o recálculo!

5. Programação dinâmica
• Decomposição do problema em subproblemas.
• Pense na solução para cada subproblema.
• Subproblemas sobrepostos: resolve um determinado subproblema e mais a
frente precisa do resultado daquele subproblema que já foi resolvido.
• Reutilização das soluções (eficiência): podemos sair de um problema
exponencial para polinomial...
• Otimalidade: solução ótima é composta de soluções ótimas dos subproblemas
• O Dijkstra é só guloso? Não, é uma combinação de guloso e PD!
• Discussão: http://codeforces.com/blog/entry/20503

6. Programação dinâmica
• Hello World – não adianta, sempre Fibonacci estará presente!
• Normalmente o cálculo de Fibonacci é feito da seguinte forma:
• Isso é eficiente?

7. Programação dinâmica
• fib(6)
6
5 4
4 3 3 2
Ineficiente, já calculou o fib(3)... vai calcular novamente?

8. Programação dinâmica
• fib(6)
6
5 4
4 3 3 2
Temos repetições de subproblemas...

9. Programação dinâmica
• fib(6)
6
5 4
4 3 3 2
A abordagem é exponencial 

10. Programação dinâmica
• fib(6)
6
5 4
4 3 3 2
Se os subproblemas se repetem, basta guardar os
resultados dos problemas já resolvidos!

11. Programação dinâmica
• Como usar PD? Basta fazer uma memorização dos resultados:
memorizando o resultado...
já calculei?

12. Programação dinâmica
• Como usar PD? Basta fazer uma memorização dos resultados:
Transformamos algo exponencial em linear.

13. Programação dinâmica
• Essa é uma abordagem top-down , ou seja, tentamos calcular o fib(n)
antes de todo mundo...

14. Programação dinâmica
• Abordagem bottom-up:
• Removemos a chamada recursiva, criamos um array para guardar os
resultados e fomos construindo de trás para frente!

15. Problema da mochila 0-1
• Digamos que você possui objetos onde cada objeto possui um peso e valor.
• Digamos que você também possui uma mochila que possui uma capacidade
máxima (peso máximo suportado).
• Seu objetivo é: levar um conjunto de objetos cujo valor total seja máximo e o
peso total não ultrapasse a capacidade da mochila.
• Resumindo: você quer maximizar o valor de forma que não ultrapasse a
capacidade máxima da mochila.

16. Problema da mochila 0-1
• Objetos: X1, X2, ... , Xn
• Valores: V1, V2, ... , Vn
• Pesos: P1, P2, ... , Pn
• Peso máximo da mochila: P
• Qual aplicação disso?
• Maximizar o lucro...
• Maximizar a quantidade de brinquedos...
• Maximizar a felicidade...

17. Problema da mochila 0-1
• Trata-se de um problema difícil, vários refinamentos foram feitos até se chegar
a uma solução legal... Don’t panic!
• Como encontrar uma composição de objetos que maximize o valor
respeitando a restrição da capacidade máxima da mochila?
• Uma abordagem: guloso.

18. Problema da mochila 0-1
• Utilizando abordagem gulosa:
• Ordena os objetos pelo valor máximo e vai pegando cada objeto se não ultrapassar a
capacidade máxima da mochila.
• Também pode-se ordenar pelo (valor / peso)...
• Garante chegar a solução ótima global?
• De acordo com a estratégia gulosa de pegar pelo maior valor, colocaria o item X3 (maior
valor), mas não poderia colocar nenhum item a mais. Uma solução melhor é pegar os
itens X1 e X2 totalizando o valor 35 (> 30).
Capacidade: 20 X1 X2 X3
Pi 10 10 20
Vi 15 20 30

19. Problema da mochila 0-1
• Por que 0-1 ? Ou o objeto está ou não está na mochila.
• Estratégia gulosa pode garantir uma boa aproximação, mas não garante a
solução ótima global. Vamos tentar por programação dinâmica...
• Temos que reduzir o problema, chegarmos a uma solução recursiva.
• Com a redução do problema, teremos subproblemas.
• Resolve os subproblemas (cálculos menores)...
• Faz-se uma observação e...
• É difícil esboçar um algoritmo!

20. Problema da mochila 0-1
• Qual a observação?
“O objeto Xn pode está ou não está na solução ótima.”
20

21. Problema da mochila 0-1
• Se um objeto Xn está na mochila, então a composição ótima da mochila é esse
objeto mais os demais descontando o peso desse objeto!
• Considere P (capacidade da mochila) = 20.
• Pn = 8 (peso do objeto “n”).
• A mochila terá (Xn + (n – 1)) objetos cujo peso máximo é 12 (descontou peso do objeto).
• É como se tivesse compondo uma outra mochila...
• Se o objeto não está na solução ótima, então a solução ótima é a mochila com
peso original composta pelos (n – 1) elementos.
• Compara-se o máximo desses dois casos, queremos maximizar...
21

22. Problema da mochila 0-1
• Se Xn pertence à solução, então o valor dessa solução será:
• Vn + (valor de uma solução ótima com uma mochila de capacidade P – Pn) considerando
os (n – 1) primeiros itens.
• Como descrevemos isso?
• Como transformar numa solução?
22

23. Problema da mochila 0-1
• Temos os parâmetros:
• Conjuto dos objetos
• Peso da mochila
• Como captar esses parâmetros?
• f(i, p) -> valor ótimo considerando os “i” primeiros itens e uma mochila de
capacidade p.
f(i, p)
23
objetos que estou considerando,
os “i” primeiros objetos
p é p peso que a mochila suporta

24. Problema da mochila 0-1
• Se Xn está na solução ótima:
• f(n – 1, p – pn) + Vn
• (n – 1) -> considera agora somente os “n – 1” primeiros itens.
• (p – pn) -> desconta o peso (pn) do objeto “n”. “p” é a capacidade da mochila.
• Se o objeto “n” está na solução ótima, ele leva o valor dele, por isso o “+ Vn”.
• Se Xn não está na solução ótima:
• f(n – 1, p)
• (n – 1) -> considera agora somente os “n – 1” primeiros itens.
• p -> não desconta o peso dele, pois ele não está na solução ótima...
• Resolva fazendo o máximo (max) desses dois casos...
24

25. Problema da mochila 0-1
• O objetivo é o cálculo do f(n), ou seja, para “n” objetos.
• Iremos resolver de baixo para cima (bottom-up).
• Calculando valores pequenos e aumentando os valores da função “f” até
chegar no f(n, p).
25

26. Problema da mochila 0-1
• Recorrência:
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
• f(i, p) = f(i – 1, p) se pi > p
• O i-ésimo item cabe na mochila? Se pi > p, então ele não cabe na mochila, esqueça ele e
olhe para os “i – 1” primeiros itens.
• f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
• Se pi <= p, calcula-se o máximo dos 2 casos: está ou não na mochila?
• O primeiro considera o item na mochila e o segundo não considera o item na mochila.
26

27. Problema da mochila 0-1
27
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p

28. Problema da mochila 0-1
28
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
f(0, p) = f(i, 0) = 0
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0
2 0
3 0
4 0
i

29. Problema da mochila 0-1
29
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
Vamos calcular o f(1, 1): 1 item e mochila de peso 1
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 ?
2 0
3 0
4 0
i

30. Problema da mochila 0-1
30
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
P1 > P? 2 > 1? Sim, então não cabe, resposta: f(i – 1, 1) = f(1 – 1, 1) = f(0, 1) = 0
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 ?
2 0
3 0
4 0
i

31. Problema da mochila 0-1
31
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
Vamos calcular o f(1, 2): 1 item e mochila de peso 2
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 0 ?
2 0
3 0
4 0
i

32. Problema da mochila 0-1
32
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
P1 > P ? 2 > 2 ? Não, então vamos calcular o max ...
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 0 ?
2 0
3 0
4 0
i

33. Problema da mochila 0-1
33
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
f(i – 1, p – pi) + vi = f(0, 0) + 10 = 0 + 10 = 10
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 0 ?
2 0
3 0
4 0
i

34. Problema da mochila 0-1
34
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
e f(i – 1, p) = f(0, 2) = 0
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 0 ?
2 0
3 0
4 0
i

35. Problema da mochila 0-1
35
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
max(10, 0) = 10
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0 0
1 0 0 10
2 0
3 0
4 0
i

36. Problema da mochila 0-1
36
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
depois de implementar e olhar o resultado da matriz...
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

37. Problema da mochila 0-1
37
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
f(4, 7) é o valor máximo
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

38. Problema da mochila 0-1
38
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
P4 > P ? 5 > 7 ? Não, então vamos calcular o max ...
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

39. Problema da mochila 0-1
39
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
f(3, 2) + v4 = 10 + 24 = 34
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

40. Problema da mochila 0-1
40
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
f(3, 7) = 32
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

41. Problema da mochila 0-1
41
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
max( f(3, 2) + 24 ; f(3, 7) ) = max(34, 32) = 34
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 ?
i

42. Problema da mochila 0-1
42
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
34 é o valor máximo!
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 34
i

43. Problema da mochila 0-1
43
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
Qual a composição? Guarde os apontadores 
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 34
i

44. Problema da mochila 0-1
44
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
De onde o 34 veio? Do f(3, 2), então o X4 faz parte da solução.
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 34
i

45. Problema da mochila 0-1
45
P: 7 X1 X2 X3 X4
Vi 10 7 25 24
Pi 2 1 6 5
f(i, p) = f(i – 1, p) se pi > p
f(i, p) = max{ f(i – 1, p – pi) + vi, f(i – 1, p) } se pi <= p
De onde veio f(1, 2) ? Veio do f(0, 0) + 10, então o X1 faz parte da solução.
0 1 2 3 4 5 6 7 P
0 0 0 0 0 0 0 0 0
1 0 0 10 10 10 10 10 10
2 0 7 10 17 17 17 17 17
3 0 7 10 17 17 17 25 32
4 0 7 10 17 17 24 31 34
i

46. Problema da mochila 0-1
• Complexidade: O(n * P)
• “n” é a quantidade de itens.
• “P” é a capacidade máxima da mochila.
• Depende do “P”, portanto, é pseudo-polinomial.

47. Problema da mochila 0-1
• Implementação em C++:
• https://goo.gl/87o8U9
• Vídeo-aula:
• https://goo.gl/9syeQP
• Dúvidas?
• mcastrosouza@live.com