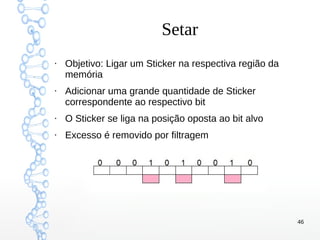
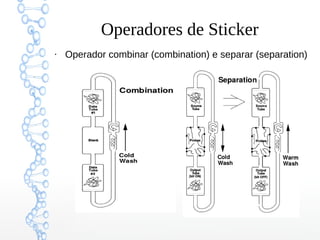
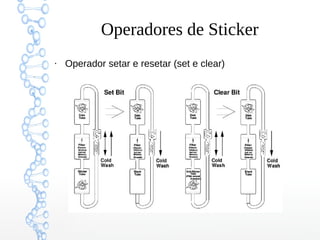
O documento descreve um modelo computacional baseado em fitas de DNA chamado "Sticker Based Model". O modelo representa informação usando fitas de DNA divididas em regiões e "stickers" complementares que se ligam às regiões para representar bits. O modelo suporta operações básicas como combinar, separar, definir e resetar bits manipulando a ligação e remoção dos stickers.





























![31
Set
def set(self, tube, bit):
for strand in self.tubes[tube]:
strand[bit] = 1
print('set:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-31-320.jpg)
![32
Clean
def clear(self, tube, bit):
for strand in self.tubes[tube]:
strand[bit] = 0
print('clear:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-32-320.jpg)
![33
Separate
def separate(self, bit, tube_origin, tube_on,
tube_off=None):
tube1 = []
tube2 = []
for strand in self.tubes[tube_origin]:
if strand[bit]:
tube1.append(strand)
else:
tube2.append(strand)
if tube_off == None:
tube_off = tube_origin
else:
del(self.tubes[tube_origin])
self.tubes[tube_on] = tube1
self.tubes[tube_off] = tube2
print('sep:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-33-320.jpg)
![34
Combine
def combine(self, tube1, tube2, tube_destination=None):
t1 = self.tubes[tube1] if tube1 in self.tubes else []
t2 = self.tubes[tube2] if tube2 in self.tubes else []
result_tube = t1 + t2
if tube2 in self.tubes:
del(self.tubes[tube2])
if tube_destination == None:
tube_destination = tube1
else:
del(self.tubes[tube1])
self.tubes[tube_destination] = result_tube
print('comb:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-34-320.jpg)

![36
Discard
def discard(self, tube):
if tube in self.tubes:
del(self.tubes[tube])
print('disc:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-36-320.jpg)

![38
Init
def init(self, tube_name):
tube = []
for i in product(*[(0, 1)] * self.l):
tube.append(list(i) + [0] * (self.k-self.l))
self.tubes[tube_name] = tube
print('init:t', self.tubes)](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-38-320.jpg)



![42
Independent Set no Simulador
from sticker import Stickers
s = Stickers(5, 5)
s.init(0)
edges = ((0, 4), (4, 1), (1, 3), (3, 2))
for e in edges:
s.separate(e[0], 0, 1)
s.separate(e[1], 1, 2, 3)
s.combine(0, 3)
for i in range(1, 5):
s.discard(i)
for i in range(5):
for j in range(i, -1, -1):
s.separate(i, j, -(j+1))
s.combine(j+1, -(j+1))
for a in range(6):
if s.tubes.get(a):
print(a, s.tubes[a])
break](https://image.slidesharecdn.com/slides-150521000006-lva1-app6891/85/Computacao-com-DNA-Modelo-baseado-em-Stickers-42-320.jpg)