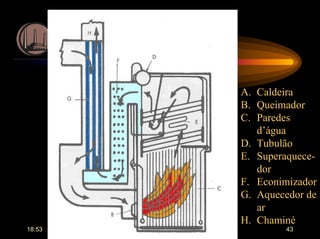
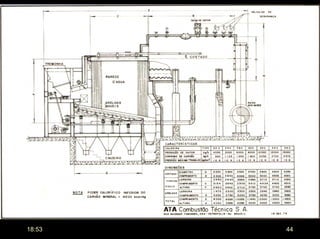
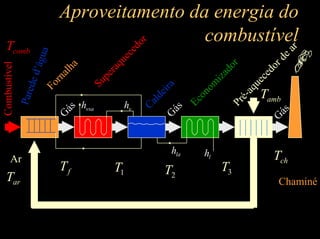
O documento discute considerações gerais sobre transferência de calor em geradores de vapor, incluindo como dimensionar termicamente paredes d'água e feixes de tubos para minimizar custos e otimizar aproveitamento de energia. Também aborda cálculos iterativos para determinar temperaturas dos gases na câmara de combustão e superfícies irradiadas, além de coeficientes de transferência de calor.




![cinzagáslcombustívearcombustãonagerado QQQQQ &&&&& +=++
PciBQ combustãonagerado .=&
( )ambarar
r
arar TTCpVBQ −= ..&
( )ambcombcomblcombustíve TTCpBQ −= .&
( )ambfg
r
gásgás TTCpVBQ −= ..&
[ ] ( )ambfczcinza TTCpCzBQ −= ..&
lcombustívearcombustãonageradodisponível QQQQ &&&& ++=](https://image.slidesharecdn.com/transfdecaloremcaldeger-150421193618-conversion-gate01/85/Transf-de-calor-em-cald-e-ger-5-320.jpg)
![18:53 6
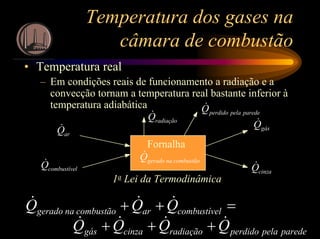
Temperatura dos gases na
câmara de combustão
• Temperatura adiabática (teórica)
( ) ( )
[ ] czg
r
g
ambcombcombambarar
r
ar
ambf
CpCzCpV
TTCpTTCpVPci
TT
..
.
+
−+−+
+=
[ ] czg
r
g
d
ambf
CpCzCpV
q
TT
.. +
+=
B
Q
q d
d
&
=
Qd = calor disponível na fornalha
.](https://image.slidesharecdn.com/transfdecaloremcaldeger-150421193618-conversion-gate01/85/Transf-de-calor-em-cald-e-ger-6-320.jpg)
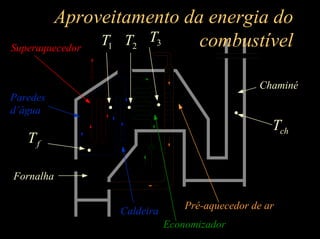
![18:53 8
Temperatura dos gases na
câmara de combustão
• Temperatura real
[ ] czg
r
g
prd
ambf
CpCzBCpVB
QQQ
TT
.... +
−−
+=
&&&
( ) ( )
[ ] czg
r
g
prambcombcombambarar
r
ar
ambf
CpCzBCpVB
QQTTCpBTTCpVBPciB
TT
....
....
+
−−−+−+
+=
&&
Qr = calor trocado por radiação com as paredes d’água
Qp = calor perdido pelas paredes, combustível não queimado, etc.
.
.](https://image.slidesharecdn.com/transfdecaloremcaldeger-150421193618-conversion-gate01/85/Transf-de-calor-em-cald-e-ger-8-320.jpg)




![18:53 13
Temperatura dos gases na
câmara de combustão
• A temperatura dos gases na câmara de combustão
é determinada por processo iterativo
( ) [ ] ( )
[ ] czg
r
g
prambczczambarar
r
ar
ambf
CpCzBCpVB
QQTTCpCzBTTCpVBPciB
TT
....
.....
+
−−−+−+
+=
&&
+
+=
iii
e
tt
r
vp
dhd
d
kNL
Q
TT
.
1
ln
1
...2 π
&
( )44
... pfir TTSQ −≅ εσ&](https://image.slidesharecdn.com/transfdecaloremcaldeger-150421193618-conversion-gate01/85/Transf-de-calor-em-cald-e-ger-13-320.jpg)











![18:53 30
Radiação gasosa em feixes
tubulares
[ ]44
..... pggg TTfAQ αεσ −=&
Qg = calor trocado por radiação gasosa
σ = constante de Stefan-Boltzman
A = área de troca de calor
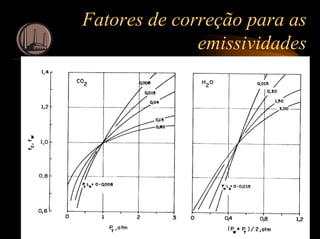
f = fator de correção para invólucros cinzas (f = 1 para corpo negro)
T = temperatura média dos gases
Tp = temperatura da parede
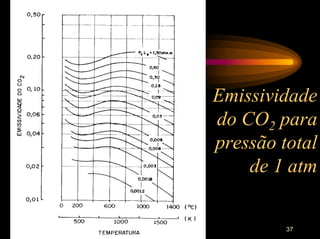
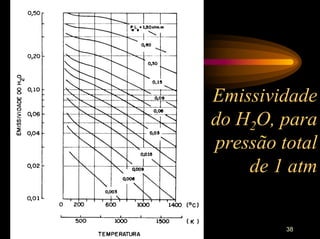
εg = emissividade do gás avaliada na temperatura T
αg = absortividade do gás para radiação proveniente do invólucro
negro na temperatura Tp
.](https://image.slidesharecdn.com/transfdecaloremcaldeger-150421193618-conversion-gate01/85/Transf-de-calor-em-cald-e-ger-30-320.jpg)