O documento aborda a analogia de Lighthill e suas premissas básicas para a dedução da lei V8 em aeroacústica. A teoria explica como o som gerado por um fluxo turbulento pode ser modelado matematicamente e estabelece simplificações úteis para a análise. A lei da oitava potência resultante é especialmente relevante para jatos frios e marcou um avanço significativo na tecnologia de turbofans.

1. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8 Fundamentos de Aeroac´ ustica
Teoria de Lighthill: Parte 1
Prof. Andrey R. da Silva
Programa de P´os-graduac¸ ˜ao em Engenharia Mecˆanica
Universidade Federal de Santa Catarina
email: andrey.rs@ufsc.br
5 de dezembro de 2014

2. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Outline
1 Analogia de Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8

3. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Outline
1 Analogia de Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8

4. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Analogia de Lighthill
O cerne do trabalho de Lighthill (1952) foi escrever, a partir da equac¸ ˜ao da
continuidade e a Equac¸ ˜ao da quantidade de movimento uma forma exata da
equac¸ ˜ao de onda n˜ao homogˆenea com termos fonte que s˜ao apenas importantes
na regi ˜ao turbulenta do fluido. Algumas premissas:
A influˆencia do som gerado pelo escoamento no pr ´oprio escoamento pode
ser ignorada;
As propriedades relativas a regi ˜ao de instabilidade podem ser
determinadas, ignorando nessa regi ˜ao a produc¸ ˜ao e propagac¸ ˜ao de som.
De fato, a premissa de Lighthill ´e a de que toda a diferenc¸a entre um fluido
real e um fluido ideal pode ser visto como uma fonte sonora.

5. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Analogia de Lighthill
Problema inicial abordado por Lighthill (Howe (2002)).

6. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Analogia de Lighthill
Problema previsto pela teoria de Lighthill (Howe (2002)).

7. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Deduc¸ ˜ao da Equac¸ ˜ao de
Lighthill
Conte´udo exposto em sala - quadro negro.

8. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
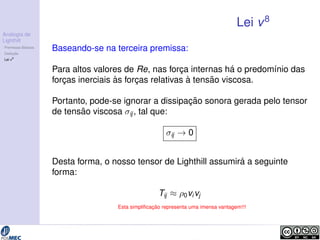
A Equac¸ ˜ao de Lighthill, expressa abaixo pode ser resolvida em
termos de c2
0 ( 0) quando conhecemos o termo Tij .
1
c2
0
@2
@t2 r2
[c2
0 ( 0)] =
@2Tij
@xi@xj
; (1)
Para tanto, a soluc¸ ˜ao ´e obtida atrav´es da integral de Green, dada
por:
c2
0 ( 0)(x; t) =
1
4
@2
@xi@xj
Z 1
1
Tij (y; t jx yj=c0)
jx yj
dy3 (2)

9. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
No entanto, o tensor de Reynolds Tij , dado por
Tij = vivj + ((p p0) c2
0 ( 0))ij ij ; (3)
pode ser simplificado mediante a algumas premissas importantes
e, ainda assim, prover uma razo´avel aproximac¸ ˜ao.

10. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Para s simplificac¸ ˜ao de Tij partiremos da seguintes premissas:
1 O fluido ´e levemente compress´ıvel, tal que M2 1;
2 O escoamento ´e frio, ou seja, as regi ˜oes de instabilidade
possuem a mesma temperatura que a regi ˜ao onde se
encontra o ouvinte (regi ˜ao linear e ideal);
3 O n´umero de Reynolds ´e alto;
4 O campo de flutuac¸ ˜ao ac´ ustica produzido n˜ao interfere no
comportamento do escoamento.
5 A fonte ´e compacta, ou seja, a sua dimens˜ao caracter´ıstica
D .

11. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Baseando-se na primeira premissa:
Neste caso, as flutuac¸ ˜oes de densidade c2
0 ( 0) ter ˜ao
O(0M2). Assim, podemos simplificar o termos de tens˜ao de
Reynolds da Eq. (3) da seguinte forma
vivj = 0(1 + O(M2))vivj 0vivj

12. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Baseando-se na primeira e segunda premissas:
A entropia ´e constante.
Al ´em disso, as poss´ıveis flutuac¸ ˜oes da velocidade do som na
regi ˜ao de instabilidade ser˜ao baixas, tal que
c2
0
c2 1 + O(M2)
Portanto, podemos escrever
p p0 c2
0 ( 0) (p p0)(1 c2
0=c) O(0M2)
extremamente pequeno
Portanto,
p p0 c2
0 ( 0) ! 0

13. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Baseando-se na terceira premissa:
Para altos valores de Re, nas forc¸a internas h´a o predom´ınio das
forc¸as inerciais `as forc¸as relativas `a tens˜ao viscosa.
Portanto, pode-se ignorar a dissipac¸ ˜ao sonora gerada pelo tensor
de tens˜ao viscosa ij , tal que:
ij ! 0
Desta forma, o nosso tensor de Lighthill assumir´a a seguinte
forma:
Tij 0vivj
Esta simplificac¸ ˜ao representa uma imensa vantagem!!!

14. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Considerac¸ ˜ao das premissas 1, 2 e 3:
Dessa maneira, assumindo todas as simplificac¸ ˜oes, a Eq.(1) se
reduz a:
p0
(x; t) =
1
4
@2
@xi@xj
Z
V
0vivj (y; t jx yj=c0)
jx yj
dV (4)
ou simplesmente,
p0
(x; t) =
1
4r
@2
@xi@xj
Z
V
0vivjdV (5)
sendo r = jx yj.

15. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Podemos assumir ainda que o som ´e produzido por
instabilidades de grandes escalas, cuja dimens˜ao caracter´ıstica ´e
D, sendo D o di ˆametro do jato.
A frequˆencia de gerac¸ ˜ao destas perturbac¸ ˜oes ´e obtida atrav´es do
n´umero de Strouhal para um jato livre e dada por:
f =
U0
D ; sendo U0 a velocidade na sa´ıda do jato
Portanto, a raz˜ao entre o di ˆametro do jato e o comprimento de
onda ac´ ustico ser´a
Df
c0
=
U0
c0
= M

16. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Pode-se assumir ainda que se D ´e a dimens˜ao caracter´ıstica, o
volume da fonte ser´a D3.
Assumimos ainda que v U0, pode-se escrever a tens˜ao de
Reynolds como 0U2
0 e, em campo distante, pode-se aproximar
@=@xi = @=c0@t 2f =c0.
Desta forma, a Eq.(5) aproxima-se de:
p0
0M2D
(x; t) 0U2
r
(6)
OBS.: A simplificac¸ ˜ao acima ignora o efeito da convec¸ ˜ao na produc¸ ˜ao do som, pois 0vi vj 0U2
0 .

17. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
Agora, lembrando que a potˆencia sonora em campo livre ´e dada
por:
I = 4jxj2 p0vr ;
tem-se que,
I 0U3
0M5D2 U8
Esta ´e a Lei da oitava potˆencia de Lighthill !!!

18. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Lei v8
A Lei da Oitava Pot ˆencia ´e bastante precisa para jatos frios.
Ela ´e respons´avel ”Revoluc¸ ˜ao do Turbofan”nos anos 60 e 70.
´E
preciso lembrar que a presenc¸a de forc¸as externas produzir´a
divergˆencias significativas da Lei v8, pois a press˜ao sonora
produzida por monopolos e dipolos e quadrupolos cresce na
proporc¸ ˜ao M2, M3 e M4, respectivamente.

19. Analogia de
Lighthill
Premissas B´asicas
Deduc¸ ˜ao
Lei v8
Fim da aula.