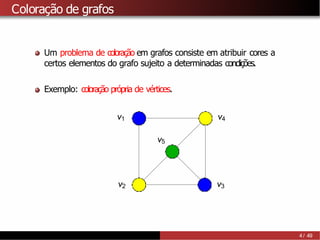
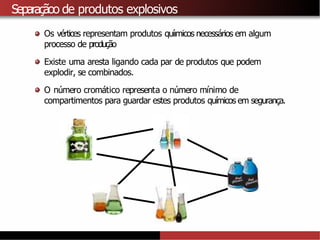
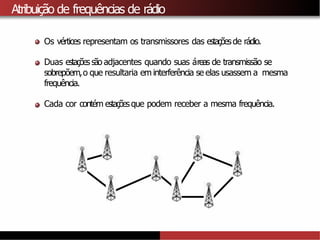
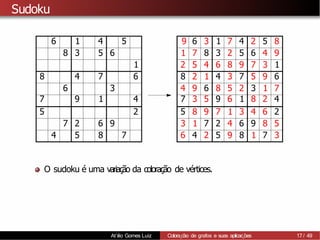
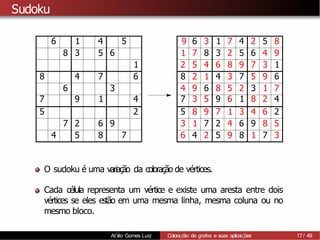
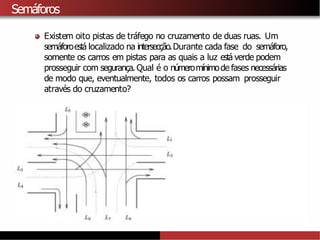
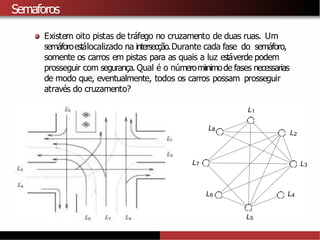
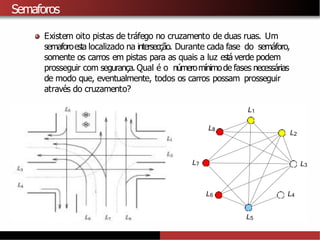
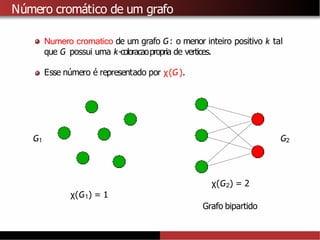
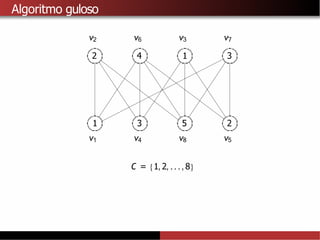
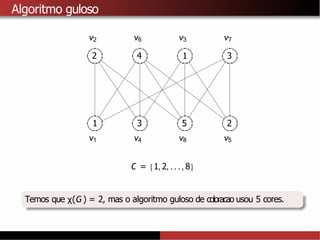
O documento discute coloração de grafos e suas aplicações. Em 3 frases: 1) A coloração de grafos envolve atribuir cores a vértices de um grafo de forma que vértices adjacentes recebam cores diferentes. 2) Isso tem aplicações como separar produtos químicos explosivos e atribuir frequências de rádio, entre outras. 3) Determinar o número cromático mínimo de um grafo é um problema NP-difícil, mas existem algoritmos como força bruta e heurísticas.

1. Coloraçãode grafos e suas aplicações
Cedemir Pereira
Mestrado de Computação Aplicada
UPF

2. Sumário
1) Introduçãoàcoloraçãode grafos
2) História
3) Aplicações
4) Algumas ideias e tentativas de solução

3. O que é um grafo?
Estrutura matemática abstrata.
Formada por dois conjuntos:
conjunto de vértices (pontos);
conjunto de arestas (arcos).

4. O que é um grafo?
Estrutura matematica abstrata.
Formada por dois conjuntos:
conjunto de vértices (pontos);
conjunto de arestas (arcos).
Pode ser usado para modelar situações do mundo real:
vértices representam pessoas, máquinas, etc.
arestas representam existência de ligação entre nós, distância
entre os nós, etc.
3 / 49

5. Coloração de grafos
Um problema de coloração em grafos consiste em atribuir cores a
certos elementos do grafo sujeito a determinadas condições
4 / 49

6. Coloração de grafos
Um problema de coloração em grafos consiste em atribuir cores a
certos elementos do grafo sujeito a determinadas condições.
Exemplo: coloração própria de vértices.
v1
v2 v3
v4
v5
4 / 49

7. Origem da coloração de grafos

8. Origem da coloração de grafos
Francis Guthrie (1852): Qualquer mapa político pode ser colorido
com no máximo quatro cores?
Francis Guthrie

9. Mapas e Grafos
Um mapa no plano pode ser representado por um grafo chamado de
grafo dual.

10. Teorema das Quatro Cores
Teorema das Quatro Cores [Appel e Haken, 1977]
Todo grafo planar possui uma coloração de vértices com no máximo
quatro cores.

11. Aplicações da coloração de vértices

12. Separaçãoo de produtos explosivos
Os vértices representam produtos quíımicos necessários em algum
processo de produção
Existe uma aresta ligando cada par de produtos que podem
explodir, se combinados.
O número cromático representa o número mı́nimo de
compartimentos para guardar estes produtos químicos em segurança.

13. Atribuição de frequências de rádio
Os vértices representam os transmissores das estaçõesde rádio.
Duas estações são adjacentes quando suas áreas de transmissão se
sobrepõem,o que resultaria em interferência se elas usassem a mesma
frequência.
Cada cor contém estaçõesque podem receber a mesma frequência.

14. Sudoku
6 1 4 5
8 3 5 6
1
8 4 7 6
6 3
7 9 1 4
5 2
7 2 6 9
4 5 8 7
9 6 3 1 7 4 2 5 8
1 7 8 3 2 5 6 4 9
2 5 4 6 8 9 7 3 1
8 2 1 4 3 7 5 9 6
4 9 6 8 5 2 3 1 7
7 3 5 9 6 1 8 2 4
5 8 9 7 1 3 4 6 2
3 1 7 2 4 6 9 8 5
6 4 2 5 9 8 1 7 3
O sudoku é uma variação da coloração de vértices.
At´ılio Gomes Luiz Colora¸cão de grafos e suas aplicac¸ões 17 / 49

15. Sudoku
6 1 4 5
8 3 5 6
1
8 4 7 6
6 3
7 9 1 4
5 2
7 2 6 9
4 5 8 7
9 6 3 1 7 4 2 5 8
1 7 8 3 2 5 6 4 9
2 5 4 6 8 9 7 3 1
8 2 1 4 3 7 5 9 6
4 9 6 8 5 2 3 1 7
7 3 5 9 6 1 8 2 4
5 8 9 7 1 3 4 6 2
3 1 7 2 4 6 9 8 5
6 4 2 5 9 8 1 7 3
O sudoku é uma variação da coloração de vértices.
Cada célula representa um vértice e existe uma aresta entre dois
vértices se eles estão em uma mesma linha, mesma coluna ou no
mesmo bloco.
At´ılio Gomes Luiz Colora¸cão de grafos e suas aplicac¸ões 17 / 49

16. Semáforos
Existem oito pistas de tráfego no cruzamento de duas ruas. Um
semáforoestá localizado na intersecção.Durante cada fase do semáforo,
somente os carros em pistas para as quais a luz está verde podem
prosseguir com segurança. Qual é o númeromínimode fases necessárias
de modo que, eventualmente, todos os carros possam prosseguir
através do cruzamento?

17. Semaforos
Existem oito pistas de tráfego no cruzamento de duas ruas. Um
semáforoestálocalizado na intersecção.Durante cada fase do semáforo,
somente os carros em pistas para as quais a luz estáverde podem
prosseguir com segurança. Qual é o númeromiınimode fases necessarias
de modo que, eventualmente, todos os carros possam prosseguir
através do cruzamento?
L1
L6 L4
L5
L2
L3
L7
L8

18. Semaforos
Existem oito pistas de tráfego no cruzamento de duas ruas. Um
semaforoesta localizado na intersecção. Durante cada fase do semáforo,
somente os carros em pistas para as quais a luz está verde podem
prosseguir com segurança. Qual é o númeromínimode fases necessárias
de modo que, eventualmente, todos os carros possam prosseguir
através do cruzamento?
L1
L6 L4
L5
L2
L3
L7
L8

19. O problema de coloração mínima

20. Definições
Não consideramos grafos com loops.
Não consideramos grafos com arestas múltiplas.
Considerados apenas grafos simples.
loop
arestas múltiplas

21. Definições
Dado um grafo simples G e v um vértice de G:
grau(v): o número de arestas incidentes em v.
grau(v1) = grau(v4) = 1
grau(v2) = grau(v3) = 3
grau(v5) = 2
v1 v2 v3 v4
v5

22. Definições
Dado um grafo simples G e v um vértice de G:
grau(v): o número de arestas incidentes em v.
grau(v1) = grau(v4) = 1
grau(v2) = grau(v3) = 3
grau(v5) = 2
v1 v2 v3 v4
v5
∆(G ) (Grau maximo de G ): é o maior grau dentre todos os graus
dos vértices de G.

23. Definicoes
Dado um grafo simples G e v um v´ertice de G:
grau(v): o número de arestas incidentes em v.
grau(v1) = grau(v4) = 1
grau(v2) = grau(v3) = 3
grau(v5) = 2
v1 v2 v3 v4
v5
∆(G ) (Grau maximo de G ): é o maior dentre todos os graus dos
vértices de G.
Dois vértices que possuem uma aresta em comum sãoditos
adjacentes.

24. Definições
α(G) = 2
Conjunto independente: subconjunto de verticesde G que não
possuem arestas em comum.

25. Definicoes
α(G) = 2
Conjunto independente: subconjunto de vérticesde G que não
possuem arestas em comum.
α(G): tamanho do maior conjunto independente de G.

26. Definicoes
Grafo bipartido: seus vertices podem ser particionados em dois
conjuntos independentes.

27. Definicoes
Grafo bipartido: seus vertices podem ser particionados em dois
conjuntos independentes.
Kn (Grafo completo com n vertices): quaisquer dois vertices sao
ligados por uma aresta.

28. Número cromático de um grafo
Numero cromatico de um grafo G: o menor inteiro positivo k tal
que G possui uma k-coloracaopropria de vertices.
Esse número é representado por χ(G).
G1 G2
χ(G1) = 1
χ(G2) = 2
Grafo bipartido

29. Número cromático de um grafo
1
1
2
2
3
v1
v2 v3
v4
v5
Grafo H
χ(H) ≤ 3
.

30. Número cromático de um grafo
1
1
2
2
3
v1
v2 v3
v4
v5
Grafo H
χ(H) ≤3.
É possı
́ vel colorir H com menos que três cores?

31. Número cromático de um grafo
1
1
2
2
3
v1
v2 v3
v4
v5
Grafo H
χ(H) ≤3.
É possı
́ vel colorir H com menos que três cores?
Como H contemum triangulo,temos que χ(H) ≥3.
Logo, χ(H) = 3.

32. Grafos bipartidos
Teorema
Um grafo G é bipartido se e somente se ele nao contem ciclo ımpar.
1
1
1 2
2
2
2
2
3
3
3
3
v1
v1
v2
v2
v3
v3 v4
v4
v5
v5
v6
v7
χ(G) = 3 χ(G) = 3

33. Grafos bipartidos
Como checar se um grafo é
bipartido?
a1
a2
a3
b1
b2
b3
A B
27 / 49

34. Algoritmo para checar se χ(G) = 2
Algorithm 1 Algoritmo para checar se G eh bipartido
Entrada: Vertice G. Vertice inicial
Comece com o vertice inicial v e pinte-o de AZUL.
2: Pinte todos os vizinhos de v de VERMELHO.
3: Continue a coloracao pintando os vizinhos dos vertices j
a coloridos,
usando ou o AZUL ou o VERMELHO. Ao atribuir cores, se
encontrarmos um vizinho colorido com a mesma cor do vertice
atual, entao o grafo naopode ser colorido com duas cores.

35. Ilustração do algoritmo

36. Ilustração do algoritmo
1

37. Ilustração do algoritmo
1
2
4
3

38. Ilustração do algoritmo
1
4
3
5
6
2
7

39. Ilustração do algoritmo
1
9
2
4
3
5
6
7
8
10

40. Ilustração do algoritmo
1
9
2
3
4
5
6
7
8
10
11
12

41. Ilustração do algoritmo
1
9
2
3
4
5
6
7
8
10
11
12
13
14
15

42. Ilustração do algoritmo
1
9
2
3
4
5
6
7
8
10
11
12
13
14
15
16

43. Limitantes inferiores para χ(G)
Mahnoticia: Ate hoje, nao se conhece nenhum bom algoritmo
para checar se um grafo G possui χ(G) = k, para k ≥3.

44. Limitantes inferiores para χ(G)
Mah noticia: Ate hoje, nao se conhece nenhum bom algoritmo
para checar se um grafo G possui χ(G) = k, para k ≥3.
Dado um grafo G , gostariamosde determinar limitantes inferiores e
superiores para χ(G).

45. Limitantes inferiores para χ(G)
a2
a3
a4
Mahnoticia: Atehoje, naoseconhece nenhum bom algoritmo
para checar se um grafo G possui χ(G) = k, para k ≥3.
Dado um grafo G , gostariamosde determinar limitantes inferiores e
superiores para χ(G).
a1
a5
a6
a7
χ(G) ≤ 4

46. Limitantes inferiores para χ(G)
a2
a3
a4
Mah noticia: Atehoje, nao conhece nenhum bom algoritmo
para checar se um grafo G possui χ(G) = k, para k ≥3.
Dado um grafo G , gostariamosde determinar limitantes inferiores e
superiores para χ(G).
a1
a5
a6
a7
χ(G) ≤4
Limitante 1: Para todo grafo G, χ(G) ≥ω(G).

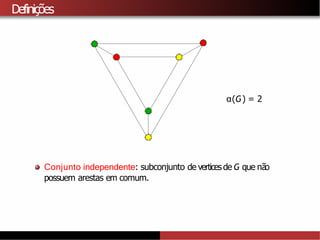
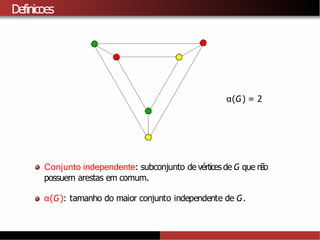
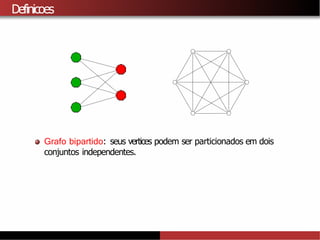
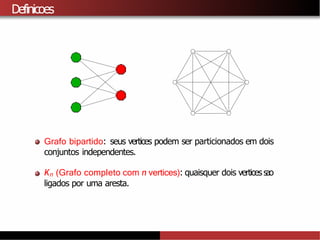
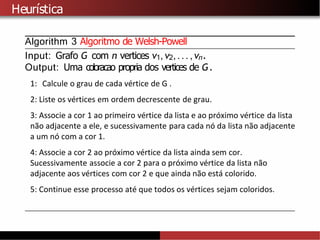
47. Limitantes inferiores para χ(G)
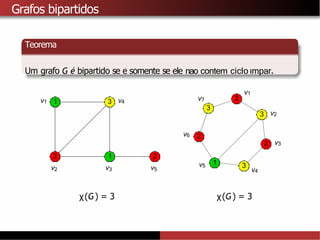
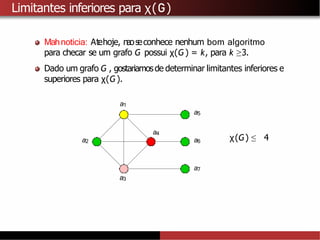
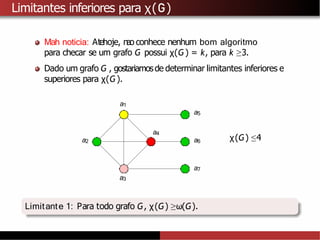
Manoticia: Existe um grafo G sem triangulos e com numero cromatico
χ(G) = k, para todo k ≥1. [Mycielski, 1955]
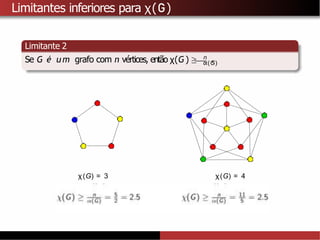
χ(G) = 1 χ(G) = 2 χ(G) = 3 χ(G) = 4
31 / 49

48. Limitantes inferiores para χ(G)
Limitante 2
α(G)
Se G é um grafo com n vértices, então χ(G ) ≥ n .
χ(G) = 3 χ(G) = 4

49. . . . e os algoritmos para colorir?

50. Complexidade da Coloracao de Vertices
(Garey e Johnson, 1974): O problema de achar o numero
cromático de um grafo é NP-difı́cil.

51. Algoritmo de força bruta
Seja G um grafo simples com n v´ertices.
kn
v1 v2 v3 v4 v5 vn
k k k k k k =

52. Algoritmo de força bruta
Seja G um grafo simples com n v´ertices.
v1 v2 v3 v4 v5 vn
k k k k k k = kn
O algoritmo de forcabruta busca por uma k-coloracaode G
considerando cada uma das kn atribuicoespossiveis e checa se cada
uma delas é correta.

53. Algoritmo de força bruta
Seja G um grafo simples com n v´ertices.
v1 v2 v3 v4 v5 vn
k k k k k k = kn
O algoritmo de forcabruta busca por uma k-coloracaode G
considerando cada uma das kn atribuicoes possiveis e checa se cada
uma delas é correta.
Para calcular χ(G ), este procedimento é testado
k = 1, . . ., n −1.
=⇒ Computacionalmente inviavel para grandes instancias.

54. Algoritmo guloso
Algoritmo guloso é aquele que sempre realiza a escolha que
parece ser a melhor no momento, fazendo uma escolha otima local,
na esperanca de que esta escolha leve atéa solução otima global.
– Ele nunca volta atras.

55. Algoritmo guloso
Algoritmo guloso é aquele que sempre realiza a escolha que
parece ser a melhor no momento, fazendo uma escolha otima local,
na esperanca de que esta escolha leve até a solução otima global.
– Ele nunca volta atras.
“Como na vida real, algoritmos gulosos, algumas vezes podem levar a
melhor solucao, outras vezes podem levar a solucoes muito boas, e outras
vezes levara solucoesruins. O truque é determinar quando ser
ganancioso”— Ian Parberry, Problems on Algorithms.

56. Algoritmo guloso
Algorithm 2 Algoritmo Guloso para coloracaode vertices
Input: Vert
iices de G listados em ordem v1,v2, ... ,vn.
Conjunto de cores disponı́veis C = {1,2,... ,n}.
Output: Uma coloracao propria dos vertices de G.
37 / 49

57. Algoritmo guloso
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

58. Algoritmo guloso
1
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

59. Algoritmo guloso
1
2
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

60. Algoritmo guloso
1
1
2
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

61. Algoritmo guloso
1
1
2
3
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

62. Algoritmo guloso
1
1 2
2
3
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

63. Algoritmo guloso
1
1 2
2
3
4
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

64. Algoritmo guloso
1
1 2
2 3
3
4
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

65. Algoritmo guloso
1
1 2
2 3
3
4
5
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}

66. Algoritmo guloso
1
1 2
2 3
3
4
5
v1
v2 v3
v5
v6 v7
v4 v8
C = {1, 2, . . ., 8}
Temos que χ(G) = 2, mas o algoritmo guloso de coloracao usou 5 cores.

67. Algoritmo guloso – Limitante superior
Teorema
Para todo grafo G, χ(G) ≤∆ (G) + 1.
Demonstracao:

68. Algoritmo guloso – Limitante superior
Teorema
Para todo grafo G, χ(G) ≤∆ (G) + 1.
Demonstracao:
Suponha que os vertices de G sejam listados na ordem v1,v2, . . . , vn
e que o algoritmo guloso é aplicado.

69. Algoritmo guloso – Limitante superior
Teorema
Para todo grafo G, χ(G) ≤∆ (G) + 1.
Demonstracao:
Suponha que os vértices de G sejam listados na ordem v1,v2, . . . , vn
e que o algoritmo guloso é aplicado.
1 2 3 ∆ (G)
vi
∆ (G) + 1

70. Algoritmo guloso – Limitante superior
Teorema
Para todo grafo G, χ(G) ≤∆ (G) + 1.
Demonstracao
Suponha que os vertices de G sejam listados na ordem v1,v2, . . . , vn
e que o algoritmo guloso é aplicado.
1 2 3 ∆ (G)
vi
∆ (G) + 1
Na i-esima iteracao do lacoao colorir o vertice vi , no maximo
∆(G ) cores terao sido utilizadas para colorir seus vizinhos. Se este
for o caso, entao escolhemos uma cor adicional para colorir vi .
Deste modo, teremos utilizados ∆(G ) + 1 cores para colorir G.

71. Heurı́stica
Heuristica é́ um método ou processo criado com o objetivo
de encontrar soluções para um problema. É um
procedimento simplificador que, em face de questões
difı ́ceis, envolve a substituição destas por outras de
resolução mais fácil a fim de encontrar respostas viáveis,
ainda que imperfeitas
Muitas heurı ́sticas para coloração de vértices se baseiam na
intuição de que um vértice de maior grau será mais difı ́cil de
colorir mais tarde do que um de menor grau.

72. Heurı́stica
Algorithm 3 Algoritmo de Welsh-Powell
Input: Grafo G com n vertices v1, v2,... ,vn.
Output: Uma coloracao propria dos vertices de G.
1: Calcule o grau de cada vértice de G .
2: Liste os vértices em ordem decrescente de grau.
3: Associe a cor 1 ao primeiro vértice da lista e ao próximo vértice da lista
não adjacente a ele, e sucessivamente para cada nó da lista não adjacente
a um nó com a cor 1.
4: Associe a cor 2 ao próximo vértice da lista ainda sem cor.
Sucessivamente associe a cor 2 para o próximo vértice da lista não
adjacente aos vértices com cor 2 e que ainda não está colorido.
5: Continue esse processo até que todos os vértices sejam coloridos.

73. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
b
a
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h

74. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h

75. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a
1
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h

76. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a
1
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h

77. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a
1
2
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h

78. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a
1
2
2
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h

79. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a 2
1
2
2
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h

80. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a 2
1
2
2
2
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h

81. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a 2
1
2
2
2
b
c
d
e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h
Passo 3: b e c d g f a h

82. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a 2
1
2
2
2
b
c
d
3 e
f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h
Passo 3: b e c d g f a h

83. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
a 2
1
2
2
2
b
c
d
3 e
3 f
g
h
Ordenação dos vértices
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h
Passo 3: b e c d g f a h

84. Execucao do Algoritmo de Welsh-Powell
Exemplo de uma instância e uma ordenação ruim:
1
1
2
2
2
2
a
b
c
d
3 e
3 f
g
h
Ordenação dos vértices
No entanto, χ(G) = 2,
pois G naopossui ciclo impar
Passo 1: b e c d g f a h
Passo 2: b e c d g f a h
Passo 3: b e c d g f a h

85. Limitantes superiores para χ(G)
A partir do algoritmo de Welsh-Powell tambem ehpossivelprovarque
χ(G) ≤∆ (G) + 1.
44 / 49

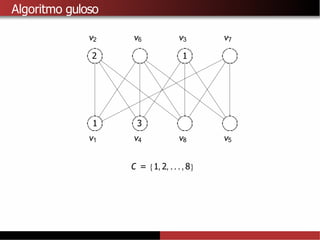
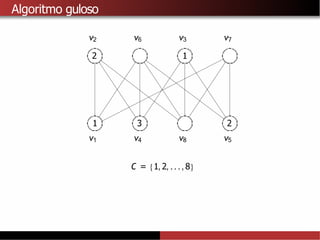
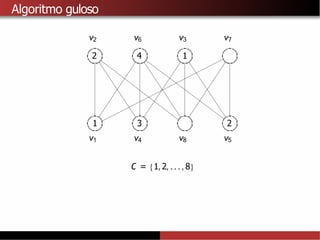
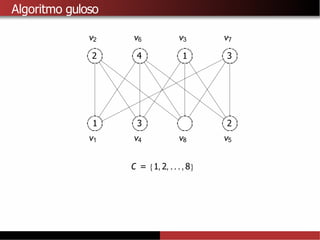
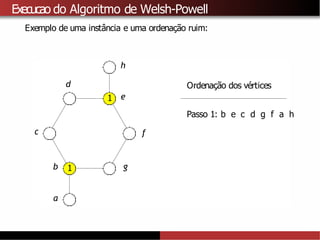
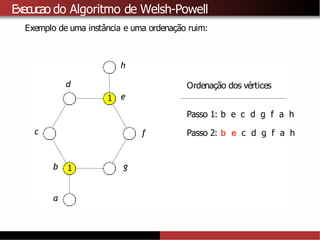
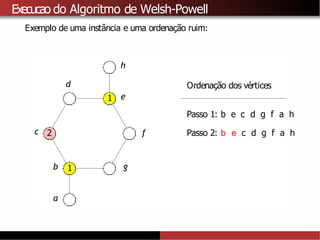
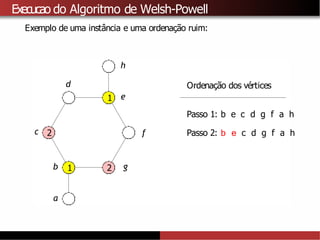
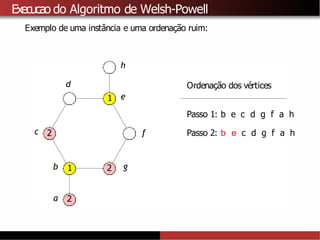
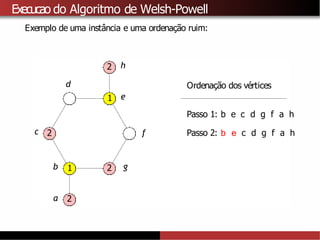
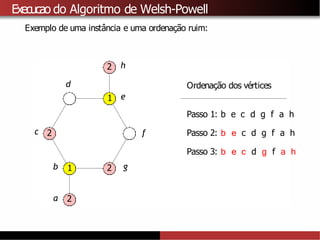
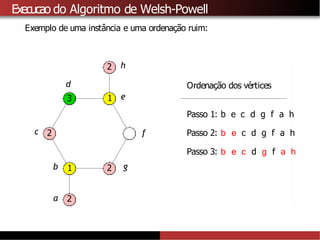
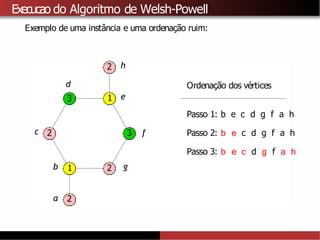
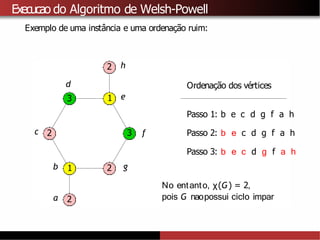
86. Limitantes superiores para χ(G)
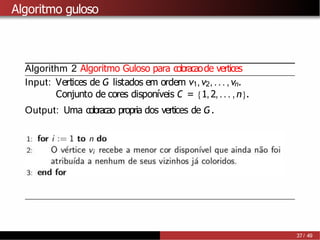
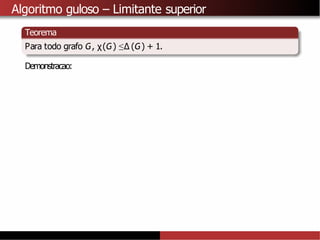
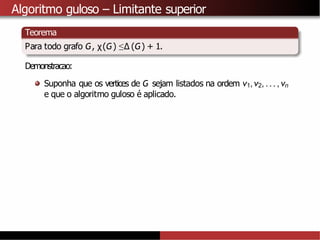
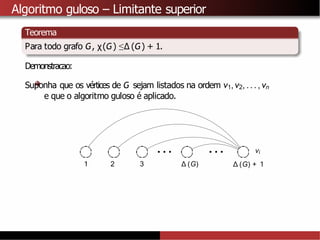
A partir do algoritmo de Welsh-Powell tambémé possível provar que
χ(G) ≤∆ (G) + 1.
Teorema [Brooks, 1941]
Se G é um grafo conexo que não é um grafo completo e nem um
ciclo impar, então χ(G) ≤∆ (G).

87. Conclusão

88. Conclusao
1. Coloracao de vertices de um grafo surgiu em 1852 a partir de um
problema de coloração de mapas.
2. Coloração de vértices possui diversas aplicações práticas.
3. Nao existem algoritmos eficientes que garantam uma coloracao
minima para grafos arbitrarios
1. Algoritmo guloso.
2. Algoritmo de Welsh-Powell.
1. Coloração de Grafos é uma área de pesquisa muito ativa em
Teoria dos Grafos.

89. Referências
Luiz, Atı́lio Gomes
- V Workshop de Tecnologia da Informação do Sertão Central
- Universidade Federal do Ceará – Campus Quixadá
- 13 de maio 2015