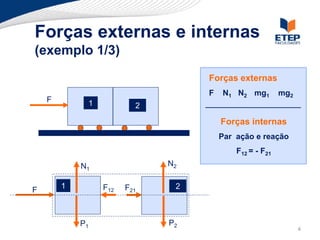
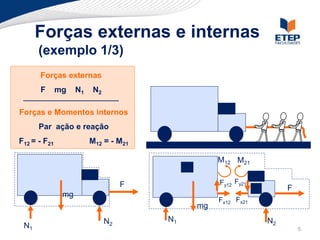
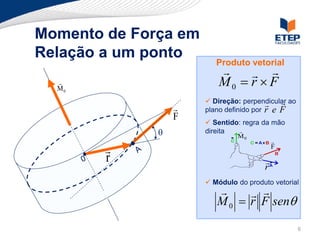
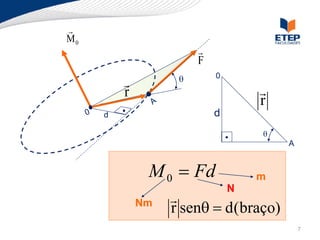
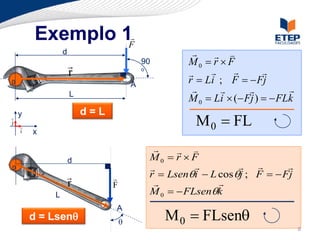
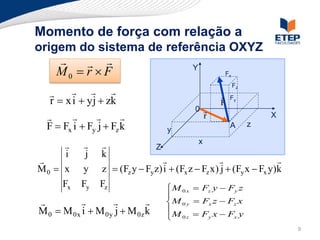
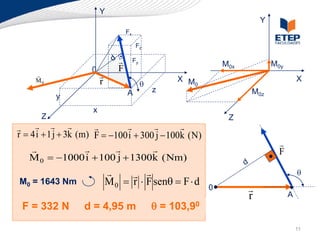
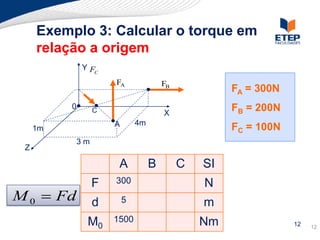
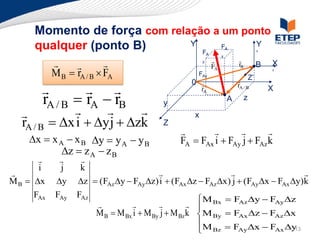
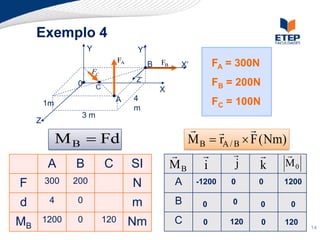
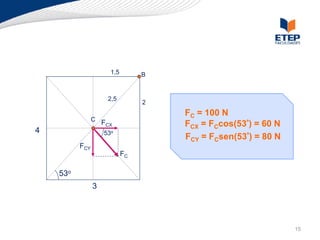
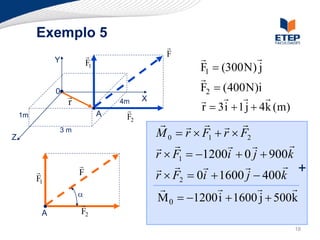
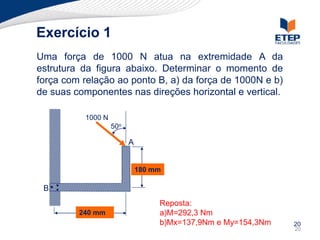
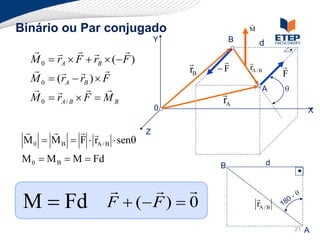
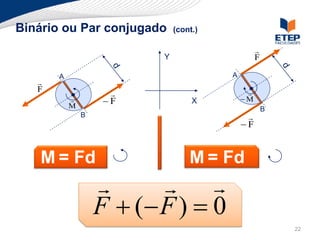
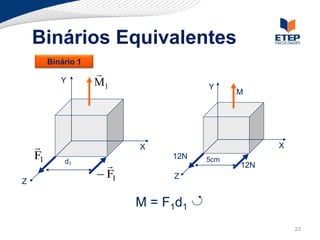
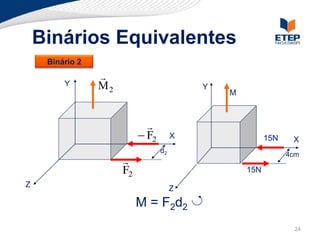
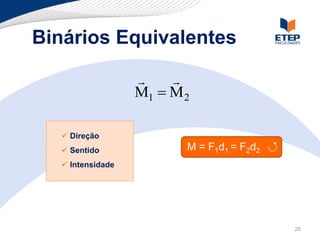
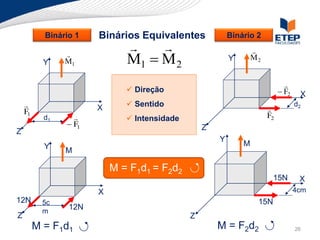
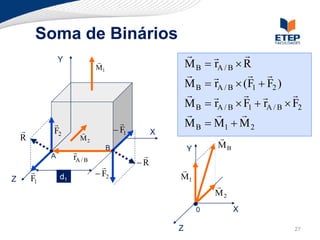
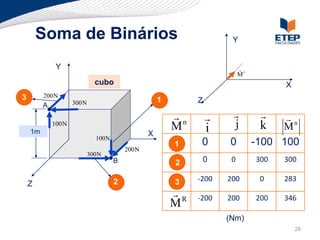
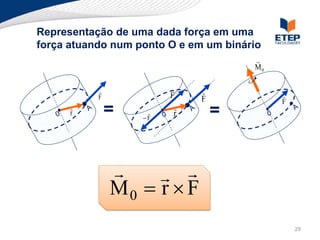
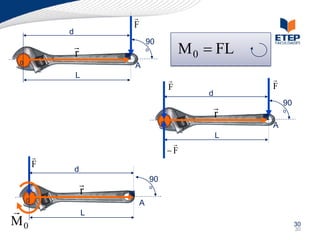
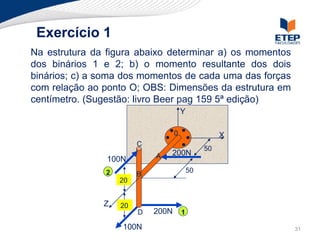
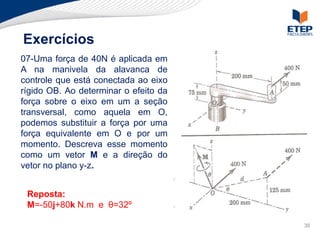
O documento apresenta os conceitos de momento de força e suas aplicações em problemas de equilíbrio de corpos rígidos. É definido o momento de força em relação a um ponto e mostrado como calcular o momento resultante a partir das forças aplicadas a um sistema. Exemplos ilustram o cálculo do momento de força em diferentes situações.

1. Estática
Seção 3 – Momento de Força
Prof. Jorge Formiga
jorge.formiga@etep.edu.br
1

2. Objetivo:
O aluno deverá aplicar o
momento de força nos
problemas de equilíbrio do corpo
rígido.
2

3. Corpo Rígido
Sistema de forças equivalentes
 Forças externas e internas
 Princípio da transmissibilidade
 Momento de força em relação a um
ponto
C
B 0.875m
Criação: DI - CETEC
A
D
E
d
0.2m
3

4. Forças externas e internas
(exemplo 1/3)
Forças externas
F N1 N2 mg1 mg2
F 1 2
Forças internas
Par ação e reação
F12 = - F21
N1 N2
F 1 F12 F21 2
P1 P2
4

5. Forças externas e internas
(exemplo 1/3)
Forças externas
F mg N1 N2
Forças e Momentos internos
Par ação e reação
F12 = - F21 M12 = - M21
M12 M21
1
F Fy12 Fy21
2 F
mg
Fx12 Fx21
mg
N2 N1 N2
N1 5

6. Momento de Força em
Relação a um ponto
Produto vetorial
  

M0
M0  r  F
 
 Direção: perpendicular ao
 plano definido por r e F
F  Sentido: regra da mão
q direita 
M0

 F
r 
r
 Módulo do produto vetorial
  
M 0  r F senq
6

7. 
M0

F
q 0

r 
r
d d
q
A
M 0  Fd m
N

 senq  d (braço)
Nm r senq  d (braço)
r
7

8. Exemplo 1F
d   
 90 M0  r  F
r o
   
0 A r  Li ; F   Fj
   
L
M 0  Li  ( Fj )   FLk
d=L
M 0  FL
 y
j

i x
  
d M0  r  F
0     
  r  Lsenqi  L cos qj ; F   Fj
r F  
L M 0   FLsenqk
M 0  FLsenq
A
d = Lsenq q
8

9. Momento de força com relação a
origem do sistema de referência OXYZ

  
F 
M0 r
M0  r  F Y
F x
Fz
    
r  x i  y j  zk F
Fy
0 
    r X
F  Fx i  Fy j  Fz k y
A z
x
   Z
i j k
   
M0  x y z  (Fz y  Fy z) i  (Fx z  Fz x ) j  (Fy x  Fx y)k
Fx Fy Fz  M 0 x  Fz y  Fy z

     M 0 y  Fx z  Fz x
M 0  M 0x i  M 0 y j  M 0z k 
 M 0 z  Fy x  Fx y
9

10. Exemplo 2
  
i j k
   
M0  4 1 3  1000 i  100 j  1300k ( Nm)
 100 300  100
M 0 x  Fz y  Fy z  ( 100) 1  300  3  1000 Nm

M 0 y  Fx z  Fz x  ( 100)  3  ( 100)  4  100 Nm

M 0 z  Fy x  Fx y  300  4  ( 100) 1  1300 Nm
10

11. Y
Y
Fx
Fz
 Fy
M0x M0y
0 F
  X M X
M0 r q 0
A z M0z
y
x
Z Z
       
r  4 i  1 j  3k (m) F  100 i  300 j  100k ( N)

    F
M 0  1000 i  100 j  1300k ( Nm)
   q
M0 = 1643 Nm M 0  r  F senq  F  d 0 
r A
F = 332 N d = 4,95 m q = 103,90
11

12. Exemplo 3: Calcular o torque em
relação a origem
Y FC
FA FB
FA = 300N
0 C FB = 200N
X
A 4m
1m FC = 100N
3m
Z
A B C SI
F 300 N
M 0  Fd d 5 m
M0 1500 Nm 12 12

13. Momento de força com relação a um ponto
qualquer (ponto B) Y F Y A
F A x ’
 
   z
FA rB B X
M B  rA / B  FA FAy ’
0   Z’
   rA
rA / B
X
rA / B  rA  rB y
A z
    x
rA / B  x i  y j  zk Z
   
x  x A  x B y  y A  y B FA  FAx i  FAy j  FAz k
z  z A  z B
  
i j k
   
M B  x y z  (FAz y  FAy z) i  (FAx z  FAz x ) j  (FAy x  FAx y)k
FAx FAy FAz M  F y  F z
     Bx Az Ay
M B  M Bx i  M By j  M Bz k M By  FAx z  FAz x

M Bz  FAy x  FAx y13

14. Exemplo 4
Y Y’
FA
B FB X’ FA = 300N
FC
Z’
0 C
FB = 200N
X
A 4 FC = 100N
1m
m
3m
Z
  
M B  Fd M B  rA / B  F ( Nm)
    
A B C SI MB i j k M0
F 300 200 N A -1200 0 0 1200
d 4 0 m B 0 0 0 0
MB 1200 0 120 Nm C 0 120 0 120
14

15. 1,5 B
2,5
2
FC = 100 N
FC = 100 N
C FCX = FCcos(53º) = 80 N
FCX FCX = FCcos(53º) = 60 N
4 53o FCY = FCsen(53º) = 60 N
FCY = FCsen(53º) = 80 N
FCY
FC
53o
3
15

16. Corpo Rígido
Sistema de forças equivalentes
 Teorema de Varignon
 Forças externas e internas
 Binário da transmissibilidade
 Princípioou Par conjugado
 Representação de uma dada força
 Momento de força em relação a um em
ponto força atuando num ponto O e em um
uma
binário
 Redução de um sistemas de forças em
uma força e um binário
C
B 0.875m
Criação: DI - CETEC
history.mcs.st-and.ac.uk
A
D
E
d 16
0.2m

17. Teorema de Varignon
Y 
F3 
F1
A
 
r F2
0
X
Z
      
r  (F1  F2  ...)  r  F1  r  F2  ...
  
F  F1  F2  ...
history.mcs.st-and.ac.uk

F : Re sul tan te das forças
17

18. Exemplo 5

 F  
Y F1
F1  (300 N) j

0 F2  (400 N)i
 X    
r 4m
A
 r  3 i  1 j  4k ( m)
1m F2
    
Z
3m
M 0  r  F1  r  F2
    
r  F1  1200i  0 j  900k

      +
F1
F r  F2  0i  1600 j  400k
   
a

M 0  1200 i  1600 j  500k
A F2
18

19. Exemplo 5
(cont.)
   
F  400 i  300 j  0k

F  F  400 2  300 2  0 2  500 N
  
M0  r  F
     
M 0  (3 i  1 j  4k )  (400 i  300 j)
   
M 0  1200 i  1600 j  500k
19

20. Exercício 1
Uma força de 1000 N atua na extremidade A da
estrutura da figura abaixo. Determinar o momento de
força com relação ao ponto B, a) da força de 1000N e b)
de suas componentes nas direções horizontal e vertical.
1000 N
50o
A
180 mm
B
Reposta:
240 mm a)M=292,3 Nm
b)Mx=137,9Nm e My=154,3Nm 20
20

21. 
Binário ou Par conjugado M
Y B d
    
M 0  rA  F  rB  ( F )    
    rB F rA / B
F
M 0  (rA  rB )  F
     A q
M 0  rA / B  F  M B rA
0 X
    Z
M 0  M B  F  rA / B  senq
M 0  M B  M  Fd d
B
  
M  Fd F  ( F )  0 
rA / B
21 A

22. Binário ou Par conjugado (cont.)

Y F
A A

F  
 F X M
M B
B 
F
M = Fd M = Fd
  
F  ( F )  0
22

23. Binários Equivalentes
Binário 1

Y M1 Y
M
 X X
F1 12N 5cm
d1
 12N
 F1 Z
Z
M = F1d1
23

24. Binários Equivalentes
Binário 2

Y M2 Y
M

 F2 X 15N X
d2
4cm

F2 15N
Z Z
M = F2d2
24

25. Binários Equivalentes
 
M1  M 2
 Direção
 Sentido M = F1d1 = F2d2
 Intensidade
25

26. Binário 1 Binários Equivalentes Binário 2
  
Y

M1 M1  M 2 Y M2

 Direção  F2 X
 X  Sentido d2
F1 
d1   Intensidade F2
 F1 Z
Z
Y
Y M
M
M = F1d1 = F2d2
15N X
X 4cm
12N 5c 15N
m
12N
Z Z
M = F1d1 M = F2d2 26

27. Soma de Binários
  
Y 
M1 MB  rA / B  R
   
MB  rA / B  (F1  F2 )
    
MB  rA / B  F1  rA / B  F2
  
  MB  M1  M 2
 F2   F1 X
R M2 
B Y MB
A
 
rA / B
 R
 
d1  F2 M1
Z F1

M2
0 X
Z 27

28. Soma de Binários Y
Y 
M1
cubo X
3 200 N
300 N 1 Z
A
n    n
100 N
M i j k M
1m X
100 N
1
1 0 0 -100 100
200 N
300 N
B 2
2 0 0 300 300
2 3
3 -200 200 0 283
Z
R -200 200 200 346
M
(Nm)
28

29. Representação de uma dada força em uma
força atuando num ponto O e em um binário

M0
  
F F 
F F

r = 
F

r =
  
M0  r  F
29

30. 
F
d
M 0  FL
90
 o
r
0 A
L 

F F
d
 90
o
r
0 A
L

F

F d
90
 o
r
0 A
 L
M0 30
30

31. Exercício 1
Na estrutura da figura abaixo determinar a) os momentos
dos binários 1 e 2; b) o momento resultante dos dois
binários; c) a soma dos momentos de cada uma das forças
com relação ao ponto O; OBS: Dimensões da estrutura em
centímetro. (Sugestão: livro Beer pag 159 5ª edição)
Y
0 X
C
50
A 200N
100N
2 50
B
20
Z 20
D 200N 1
100N 31

32. Exercícios
2- Para satisfazer limitações de projeto é necessário determinar o efeito da
força trativa F= 2 kN atuando no cabo, sobre o cisalhamento, tração e flexão
da viga em I engastada. Com esse propósito substitua a força por seu
equivalente em duas forças em A perpendicular e paralela a viga. Calcule o
torque exercido por F no ponto A.
30 cm
A
Respota: Ft=1,286 KN e
Fn=1,532 KN 200
T=459,6 Nm
300
F
B

33. Exercícios
03- Um pé-de-cabra é usado para remover um prego, como mostra a
figura abaixo. Determine o momento da força de 240 N em relação ao
ponto O, de contato entre o pé-de-cabra e o pequeno bloco de
suporte.
Reposta: Mo=84N.m
33

34. Exercícios
04- O elemento estrutural rígido está
submetido a um binário composto de um
par de forças de 100N. Substitua esse
binário equivalente, consistindo nas duas
forças P e –P, cada uma com módulo de
400N. Determine o ângulo θ apropriado.
Reposta: Mo=10N.m e θ=51,3°
34

35. Exercícios
05- Uma força F=50N é exercida sobre a alavanca do freio de mão
de mão de um automóvel onde x=250mm. Substitua a força por um
sistema força-binário equivalente no ponto O.
Reposta: Mo=17N.m 35

36. Exercícios
05- A figura representa duas engrenagens maciças submetidas às
forças de contato mostradas. Substitua as duas forças por um única
força equivalente R no eixo de rotação O e por um binário M
correspondente. Especifique os módulos de R e M.
Reposta:
R=3,56 kN , Mo=12N.m
36

37. Exercícios
06-Um força trativa T de módulo 10 kN é aplicada ao cabo preso no
topo do mastro rígido, em A e preso ao chão em B. Determine o
momento Mz de T em relação ao eixo z que passa pela base O.
Reposta:
Mz=-84,9 kN.m
37

38. Exercícios
07-Uma força de 40N é aplicada em
A na manivela da alavanca de
controle que está conectada ao eixo
rígido OB. Ao determinar o efeito da
força sobre o eixo em um a seção
transversal, como aquela em O,
podemos substituir a força por uma
força equivalente em O e por um
momento. Descreva esse momento
como um vetor M e a direção do
vetor no plano y-z.
Reposta:
M=-50j+80k N.m e θ=32º
38