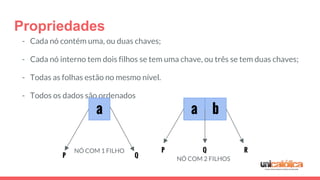
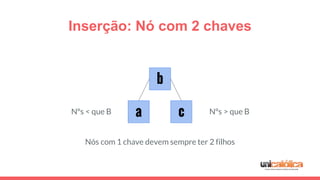
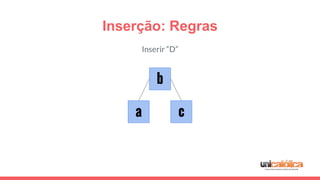
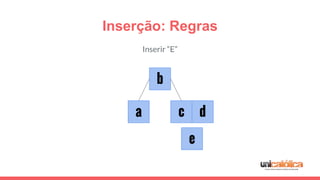
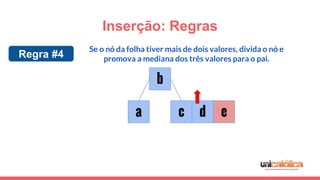
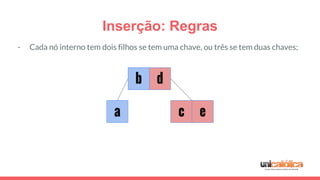
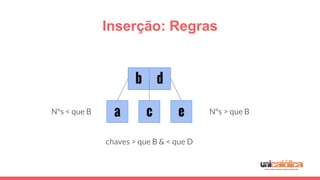
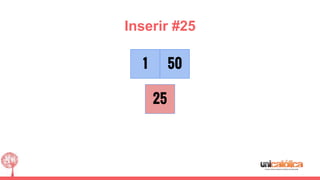
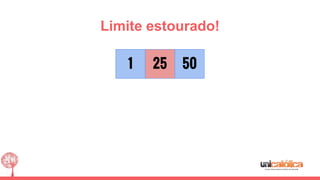
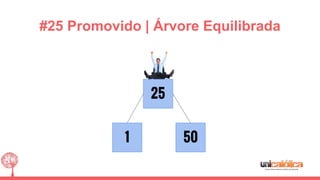
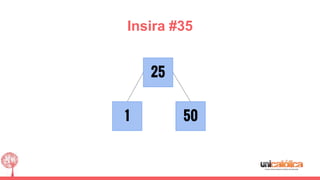
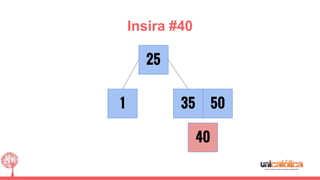
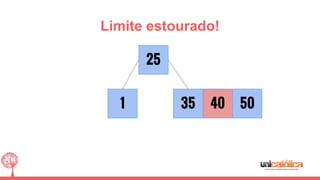
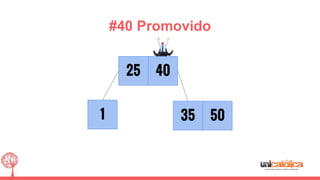
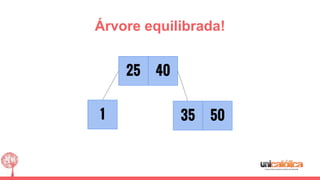
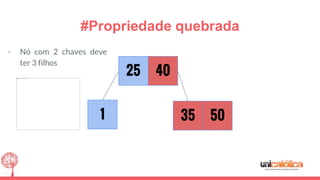
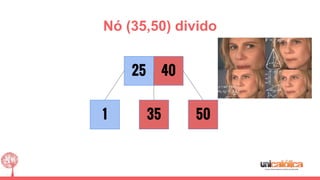
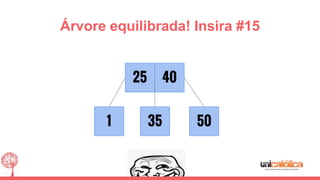
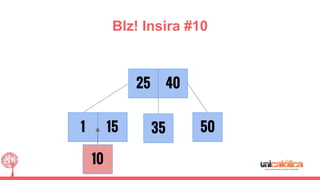
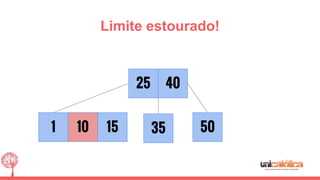
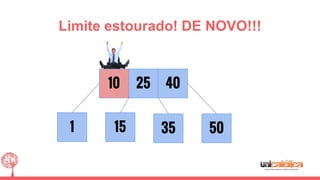
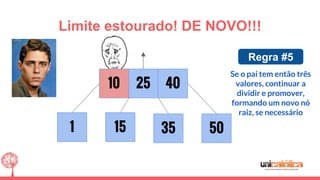
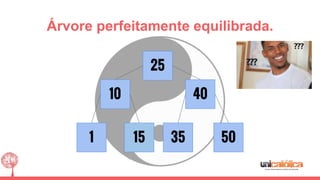
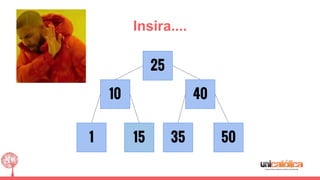
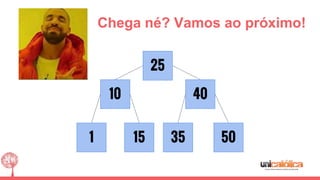
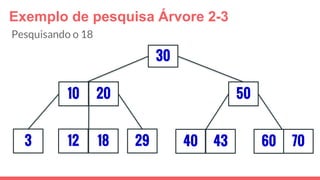
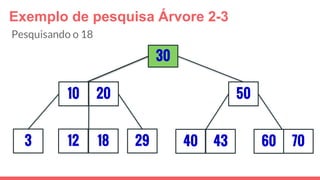
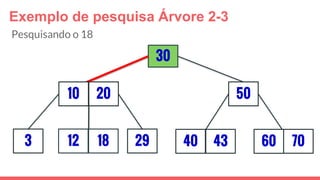
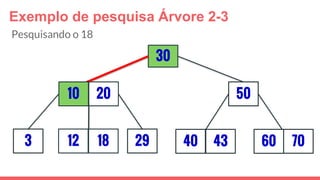
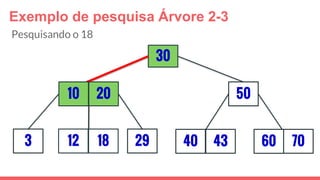
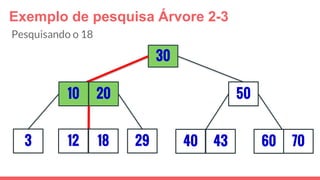
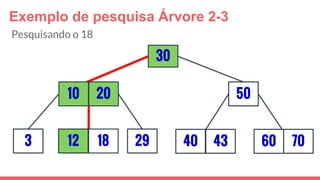
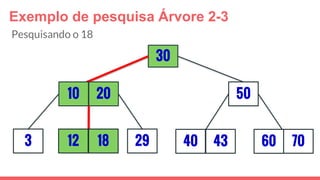
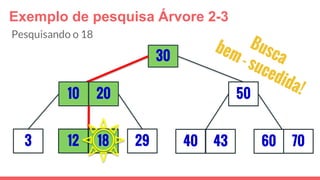
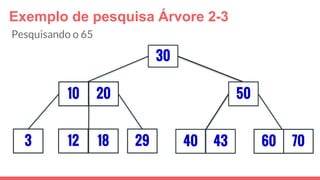
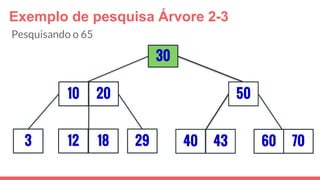
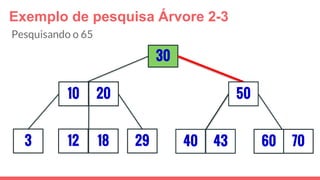
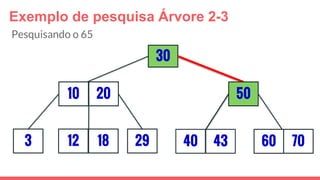
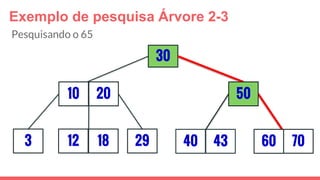
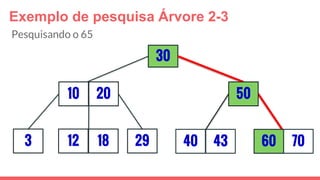
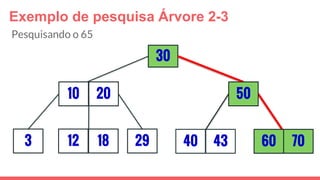
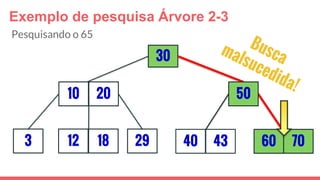
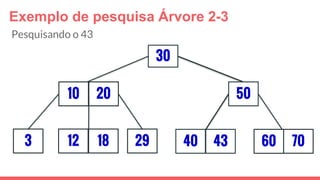
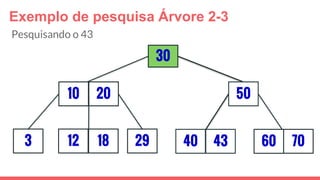
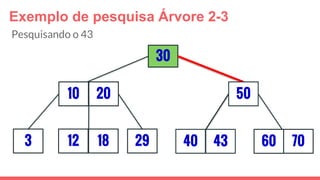
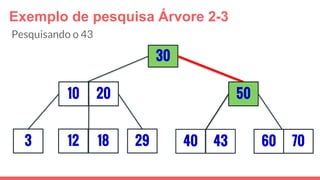
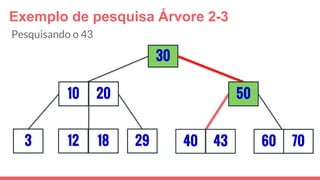
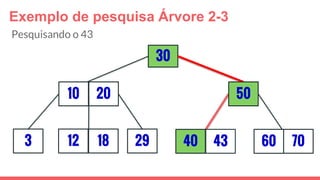
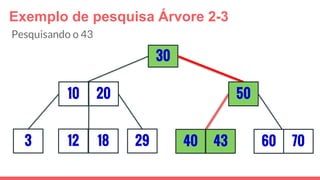
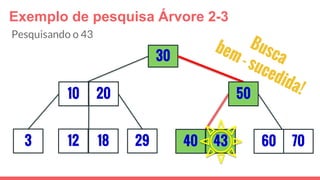
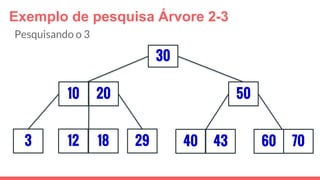
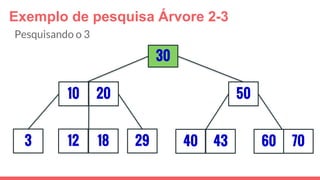
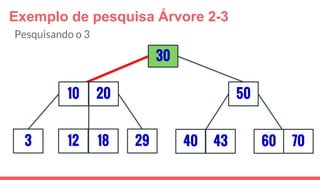
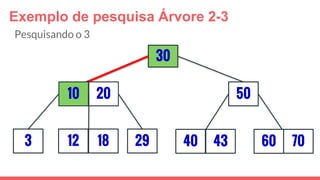
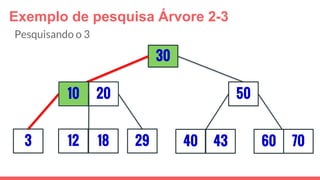
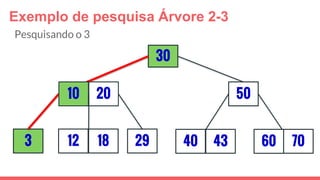
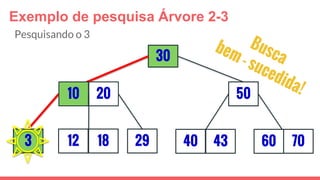
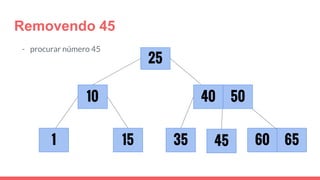
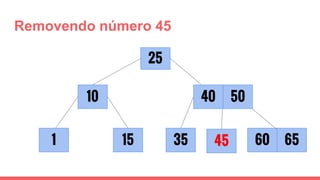
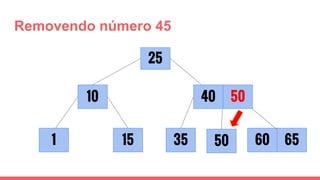
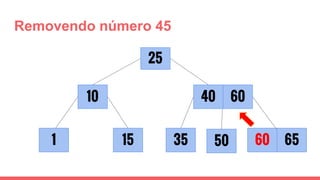
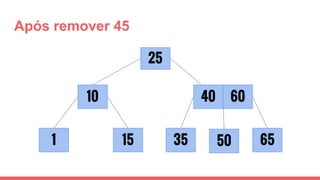
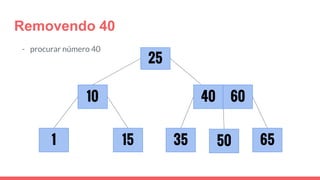
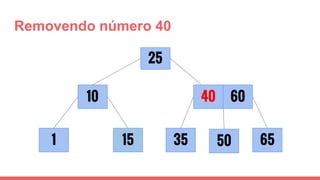
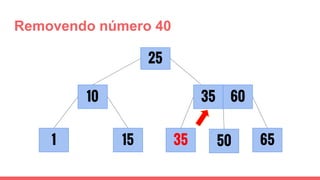
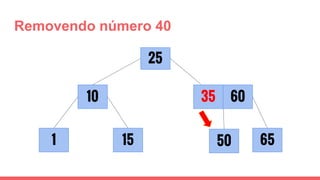
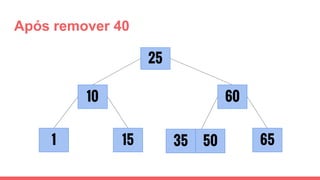
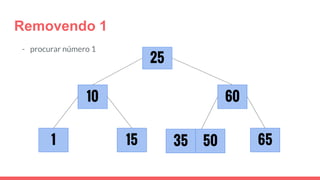
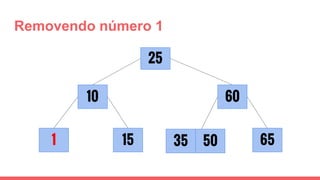
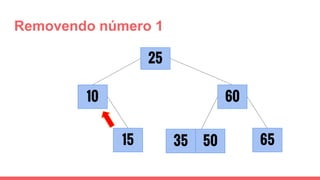
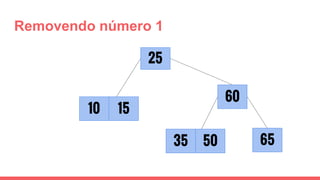
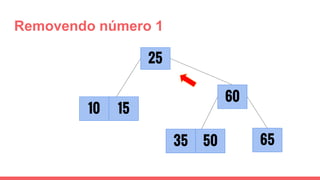
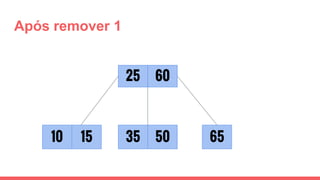
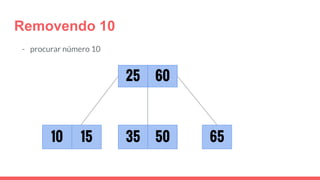
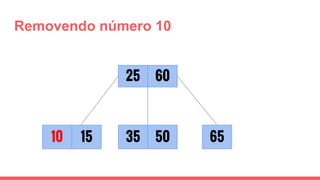
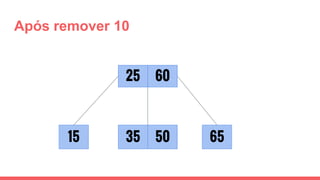
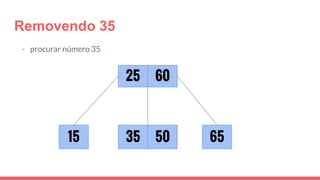
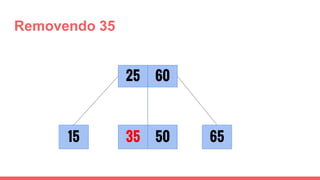
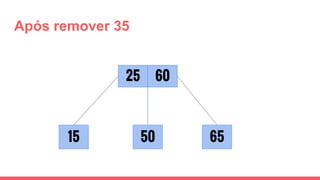
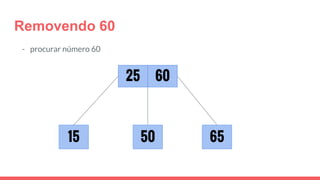
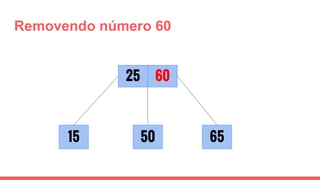
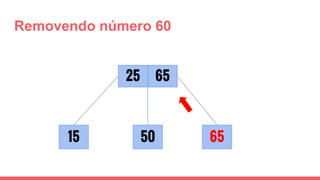
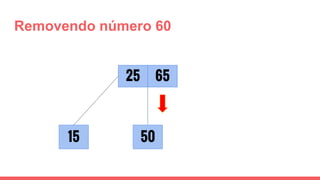
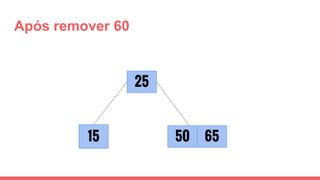
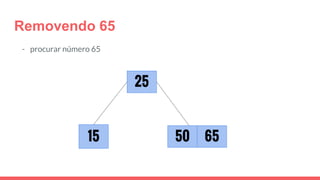
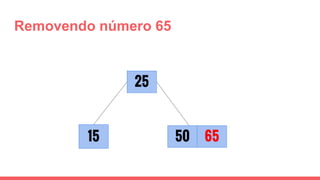
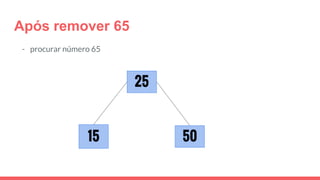
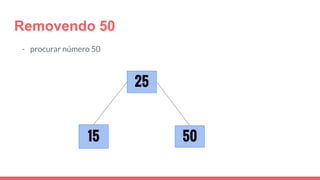
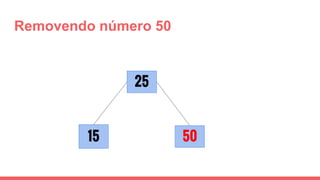
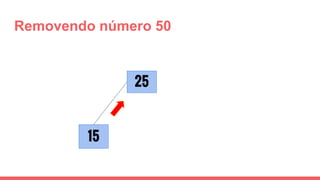
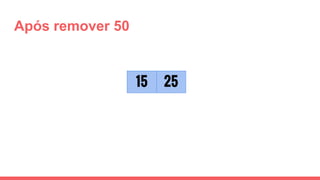
O documento discute a estrutura de dados conhecida como árvore 2-3, que foi inventada por John E. Hopcroft em 1970 e é uma estrutura de dados equilibrada, isomórfica às árvores AA. Ele aborda suas características, como fácil programação, busca rápida, vantagens e desvantagens, além de descrever os procedimentos de inserção, pesquisa e remoção de elementos nesta estrutura. Exemplos práticos são fornecidos para ilustrar o funcionamento dessas operações.

1. ÁRVORE
2-3
Estrutura de Dados II
Equipe:
Augusto Teixeira
Carlos Littbarski
Jardel Rodrigues
Victor Apuena
Professor:
Alandson Meireles

2. Informações
- A ÁRVORE 2-3 FOI A PRIMEIRA ÁRVORE MULTICAMINHOS,
INVENTADA POR J. E. HOPCROFT EM 1970.
- 2-3 árvores são uma isometria de árvores AA, o que significa que são
estruturas de dados equivalentes. Em outras palavras, para cada 2-3
árvore, existe pelo menos uma árvore AA com elementos de dados na
mesma ordem. 2-3 árvores são equilibradas, o que significa que cada
direita, centro e sub-árvore esquerda contém o mesmo ou perto da
mesma quantidade de dados.
John E. Hopcroft

3. Características
- SÃO ÁRVORES FÁCEIS DE PROGRAMAR
- SÃO ÁRVORES MULTIVIAS
- NÃO É UMA ÁRVORE BINÁRIA
- ÁRVORES 2-3 SÃO SIMILARES ÀS ÁRVORES 2-3-4.
- 2-3 DIZEM A RESPEITO À QUANTIDADE DE FILHOS QUE A ÁRVORE PODE TER
(ASSIM COMO NA 2-3-4)
- PERFEITAMENTE BALANCEADA

4. Vantagens
- Árvore perfeitamente balanceada
- Busca rápida
- Fácil implementação
- Remoção demorada
Desvantagens

5. Propriedades
- Cada nó contém uma, ou duas chaves;
- Cada nó interno tem dois filhos se tem uma chave, ou três se tem duas chaves;
- Todas as folhas estão no mesmo nível.
- Todos os dados são ordenados
NÓ COM 1 FILHO
a a b
P Q NÓ COM 2 FILHOS
P Q R

6. Vamos brincar? *-*

7. INSERÇÃO

8. Inserção: Árvore Vazia
Adicionar ‘B’

9. Inserção: Árvore Vazia
b
Se a Árvore estiver vazia:
Criar um nó e adicionar o valor ao nó
Regra #1

10. Inserção: Nó com 1 chave
b
Adicionar ‘A’
a

11. Inserção: Nó com 1 chave
b
Caso contrário, localize o nó a qual o valor pertence.
Se o nó tiver apenas 1 valor, adicione o valor no nó.
a
Regra #2
Regra #3
Inserir chave no nó sempre de forma ordenada.

12. Inserção: Nó com 2 chave
a b
c
Adicionar ‘C’

13. Inserção: Nó com 2 chaves
c
Se o nó da folha tiver mais de dois valores, divida o nó e
promova a mediana dos três valores para o pai.
a b
Regra #4
Número de chaves estouradas
Promover a mediana
Quebrar o nó e fazer a ligação

14. Inserção: Nó com 2 chaves
ca
b
Nºs > que BNºs < que B
Nós com 1 chave devem sempre ter 2 filhos

15. Inserção: Regras
c
Inserir “D”
a
b

16. Inserção: Regras
c
Inserir “E”
a
b
d
e

17. Inserção: Regras
ca
b
d e
Se o nó da folha tiver mais de dois valores, divida o nó e
promova a mediana dos três valores para o pai.Regra #4

18. Inserção: Regras
ca
b d
e
- Cada nó interno tem dois filhos se tem uma chave, ou três se tem duas chaves;

19. Inserção: Regras
ca
b d
e Nºs > que BNºs < que B
chaves > que B & < que D

20. Vamos ver se entendemos tudo?

21. Árvore vazia. Insira #50

22. Insira #1
50

23. Insira #25
1 50

24. Inserir #25
1 50
25

25. Limite estourado!
1 5025

26. #25 Promovido | Árvore Equilibrada
1 50
25

27. Insira #35
1 50
25

28. Insira #40
1 35
25
50
40

29. Limite estourado!
1 35
25
5040

30. #40 Promovido
1
4025
5035

31. 1
4025
5035
Árvore equilibrada!

32. 1
4025
5035
Só que não!

33. #Propriedade quebrada
1
4025
5035
- Nó com 2 chaves deve
ter 3 filhos

34. Nó (35,50) divido
1
4025
5035

35. Árvore equilibrada! Insira #15
1
4025
5035

36. 1 35
25
50
40
Blz! Insira #10
15
10

37. 1 35
25
50
40
Limite estourado!
1510

38. 1 35
25
50
40
Limite estourado! DE NOVO!!!
15
10

39. 25 40
Limite estourado! DE NOVO!!!
10
Se o pai tem então três
valores, continuar a
dividir e promover,
formando um novo nó
raiz, se necessário
Regra #5
1 35 5015

40. 25
40
Coisa linda de mamãe!!!
10
1 35 5015

41. Árvore perfeitamente equilibrada.
1 35
25
50
40
15
10

42. 1 35
25
50
40
Insira....
15
10

43. Chega né? Vamos ao próximo!
1 35
25
50
40
15
10

44. PESQUISA

45. Árvore 2-3
▪ Nó Simples:
▪ Contém uma chave e dois links; um link esquerdo para uma
árvore 2-3 que tem chaves menores que a chave do nó; e um
link direto para uma árvore 2-3 que tem chaves maiores;

46. Árvore 2-3
▪ Nó Duplo:
▪ Contém duas chaves e três links: um link esquerdo para uma
árvore 2-3 que tem chaves menores; e um link do meio para
uma árvore 2-3 que tem chaves entre as duas chaves do nó; e
um link direto para uma árvore 2-3 que tem chaves maiores;

47. Pesquisa em uma árvore 2-3
- Inicia-se sempre pela raiz;
- Caso o item pesquisado não se encontra na raiz, identifica o nó
filho da raiz em que o mesmo possa estar e siga para este nó;
- Se o item tiver valor maior que a raiz, siga para direita da
árvore, se não vá para esquerda;
- O processo se repete até que o item seja encontrado;

48. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

49. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

50. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

51. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

52. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

53. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

54. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

55. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

56. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 18

57. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

58. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

59. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

60. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

61. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

62. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

63. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

64. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 65

65. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

66. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

67. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

68. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

69. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

70. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

71. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

72. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 43

73. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

74. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

75. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

76. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

77. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

78. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

79. Exemplo de pesquisa Árvore 2-3
3
30
29
5010 20
12 18 40 43 7060
Pesquisando o 3

80. REMOÇÃO

81. Remoção de uma árvore 2-3
- A remoção um item de uma árvore 2-3 é aproximadamente o inverso do
processo de inserção;
- Para remover um item, devemos primeiro procurar por ele;
- Se o item a ser removido estiver em uma folha com dois itens;
- simplesmente o excluímos;
- o removemos trocando-o item da árvores;

82. Removendo 45
- procurar número 45
1 35
25
60
10
6545
40 50
15

83. Removendo número 45
1 35
25
60
10
6545
40 50
15

84. Removendo número 45
1 35
25
6015
10
6550
40 50

85. Removendo número 45
1 35
25
6015
10
6550
40 60

86. Após remover 45
1 35
25
15
10
6550
40 60

87. Removendo 40
- procurar número 40
1 35
25
15
10
6550
40 60

88. Removendo número 40
1 35
25
15
10
6550
40 60

89. Removendo número 40
1 35
25
15
10
6550
35 60

90. Removendo número 40
1
25
15
10
6550
35 60

91. Após remover 40
1
25
15
10
6535
60
50

92. Removendo 1
- procurar número 1
1
25
15
10
6535
60
50

93. Removendo número 1
1
25
15
10
6535
60
50

94. Removendo número 1
25
15
10
6535
60
50

95. Removendo número 1
25
10
6535
60
50
15

96. Removendo número 1
25
10
6535
60
50
15

97. Após remover 1
25
10 6535
60
5015

98. Removendo 10
- procurar número 10
25
10 6535
60
5015

99. Removendo número 10
25
10 6535
60
5015

100. Após remover 10
25
6535
60
5015

101. Removendo 35
- procurar número 35
25
6535
60
5015

102. Removendo 35
25
6535
60
5015

103. Após remover 35
25
65
60
5015

104. Removendo 60
- procurar número 60
25
65
60
5015

105. Removendo número 60
25
65
60
5015

106. Removendo número 60
25
65
65
5015

107. Removendo número 60
25 65
5015

108. Após remover 60
25
655015

109. Removendo 65
- procurar número 65
25
655015

110. Removendo número 65
25
655015

111. Após remover 65
- procurar número 65
25
5015

112. Removendo 50
- procurar número 50
25
5015

113. Removendo número 50
25
5015

114. Removendo número 50
25
15

115. Após remover 50
2515

116. Removendo 25
- procurar número 25
2515

117. Removendo 15
- procurar número 15
15

118. REFERÊNCIAS
USP - “Instituto de Matemática e Estatística”. Disponível em:
https://www.ime.usp.br/~gold/cursos/2002/mac2301/aulas/b-arvore/
LAFORE - ESTRUTURA DE DADOS E ALGORÍTMOS EM JAVA - 2ª EDIÇÃO
WIKIPEDIA - https://pt.wikipedia.org/wiki/%C3%81rvore_2-3
Gross, R. Hernández, J. C. Lázaro, R. Dormido, S. Ros (2001). Estructura de Datos
y Algoritmos Prentice Hall
Ellio B. Koffman Paul A. T. Olfgang (2006) : Objetos, Abstração, Estruturas de
dados e projeto usando C++

119. Muito
obrigado!!!