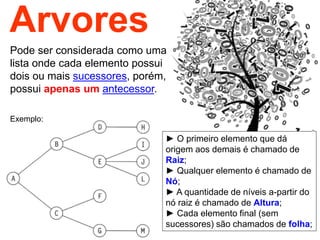
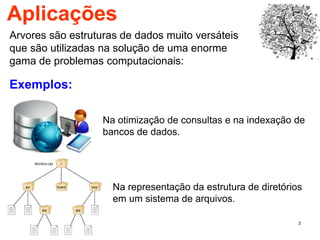
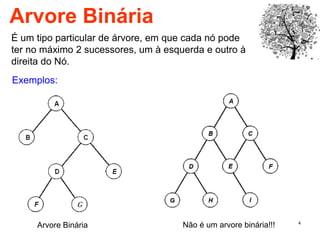
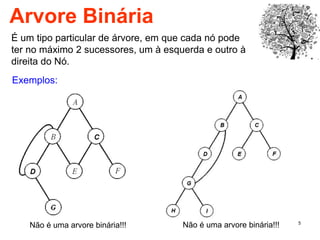
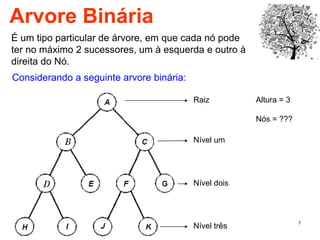
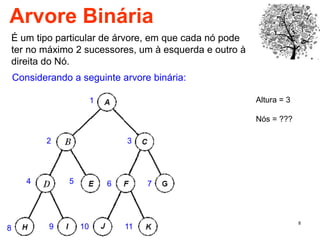
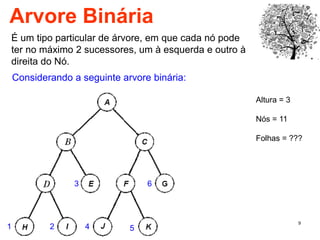
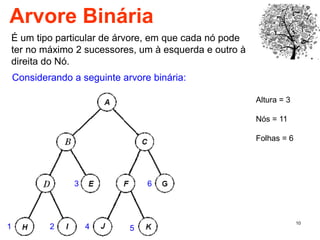
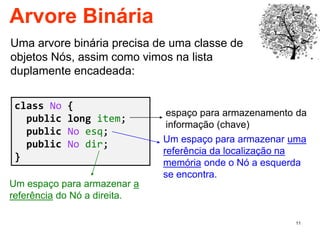
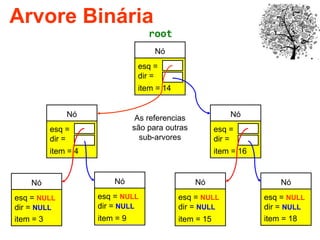
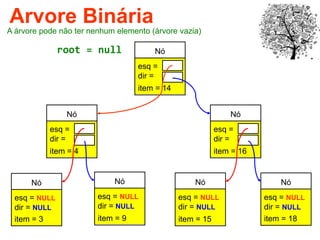
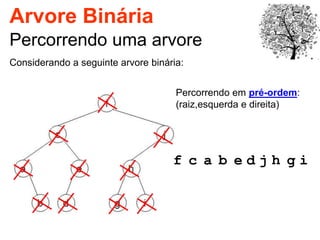
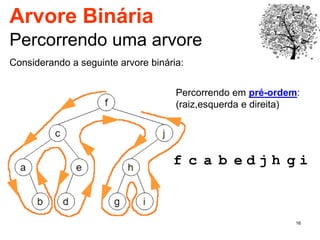
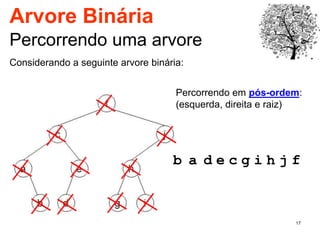
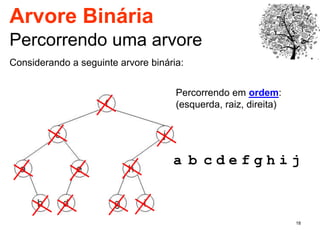
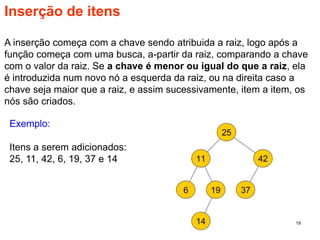
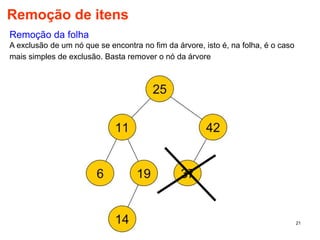
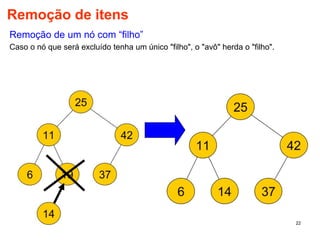
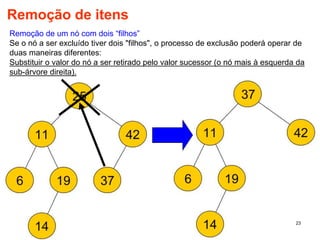
O documento discute árvores como estruturas de dados, definindo conceitos como raiz, nós, altura e folhas. Explica aplicações de árvores como indexação em bancos de dados e sistemas de arquivos. Também descreve árvores binárias e operações nelas como percorrer, inserir e remover nós.

1. Estrutura de
Dados
Arvores
profa. Divani Barbosa
Aula 13 parte 1

2. 2
Arvores
Pode ser considerada como uma
lista onde cada elemento possui
dois ou mais sucessores, porém,
possui apenas um antecessor.
Exemplo:
► O primeiro elemento que dá
origem aos demais é chamado de
Raiz;
► Qualquer elemento é chamado de
Nó;
► A quantidade de níveis a-partir do
nó raiz é chamado de Altura;
► Cada elemento final (sem
sucessores) são chamados de folha;

3. 3
Aplicações
Arvores são estruturas de dados muito versáteis
que são utilizadas na solução de uma enorme
gama de problemas computacionais:
Exemplos:
Na otimização de consultas e na indexação de
bancos de dados.
Na representação da estrutura de diretórios
em um sistema de arquivos.

4. 4
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Exemplos:
Arvore Binária Não é um arvore binária!!!

5. 5
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Não é uma arvore binária!!!Não é uma arvore binária!!!
Exemplos:

6. 6
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Exemplos:

7. 7
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Considerando a seguinte arvore binária:
Raiz
Nível um
Nível dois
Nível três
Altura = 3
Nós = ???

8. 8
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Altura = 3
Nós = ???
1
2 3
4 5 6 7
8 9 10 11
Considerando a seguinte arvore binária:

9. 9
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Altura = 3
Nós = 11
Folhas = ???
1 2
3
4 5
6
Considerando a seguinte arvore binária:

10. 10
Arvore Binária
É um tipo particular de árvore, em que cada nó pode
ter no máximo 2 sucessores, um à esquerda e outro à
direita do Nó.
Altura = 3
Nós = 11
Folhas = 6
1 2
3
4 5
6
Considerando a seguinte arvore binária:

11. 11
Arvore Binária
Uma arvore binária precisa de uma classe de
objetos Nós, assim como vimos na lista
duplamente encadeada:
class No {
public long item;
public No esq;
public No dir;
}
espaço para armazenamento da
informação (chave)
Um espaço para armazenar uma
referência da localização na
memória onde o Nó a esquerda
se encontra.
Um espaço para armazenar a
referência do Nó a direita.

12. 12
Nó
esq =
dir =
item = 14
Nó
esq =
dir =
item = 4
Nó
esq =
dir =
item = 16
Nó
esq = NULL
dir = NULL
item = 3
Nó
esq = NULL
dir = NULL
item = 9
Nó
esq = NULL
dir = NULL
item = 15
Nó
esq = NULL
dir = NULL
item = 18
As referencias
são para outras
sub-arvores
root
Arvore Binária

13. 13
Nó
esq =
dir =
item = 14
Nó
esq =
dir =
item = 4
Nó
esq =
dir =
item = 16
Nó
esq = NULL
dir = NULL
item = 3
Nó
esq = NULL
dir = NULL
item = 9
Nó
esq = NULL
dir = NULL
item = 15
Nó
esq = NULL
dir = NULL
item = 18
root = null
A árvore pode não ter nenhum elemento (árvore vazia)
Arvore Binária

14. 14
Percorrendo uma arvore
Uma operação comum é percorrer uma árvore binária,
o que consiste em visitar todos os nós desta árvore
segundo algum critério. Esse percurso, também
chamado de travessia da árvore, pode ser feito de tres
formas:
Pré-ordem:
Pós-ordem:
Primeiro visita a raiz, depois o Nó a esquerda
finalizando com o Nó a direita.
Primeiro visita o Nó a esquerda, depois o Nó a direita
finalizando com a raiz.
Ordem: Primeiro visita o Nó a esquerda, depois a raiz,
finalizando com o Nó a direita.
Arvore Binária

15. Percorrendo uma arvore
Considerando a seguinte arvore binária:
Percorrendo em pré-ordem:
(raiz,esquerda e direita)
f c a b e d j h g i
Arvore Binária

16. 16
Percorrendo uma arvore
Considerando a seguinte arvore binária:
Percorrendo em pré-ordem:
(raiz,esquerda e direita)
f c a b e d j h g i
Arvore Binária

17. 17
Percorrendo uma arvore
Considerando a seguinte arvore binária:
Percorrendo em pós-ordem:
(esquerda, direita e raiz)
fcab ed jhg i
Arvore Binária

18. 18
Percorrendo uma arvore
Considerando a seguinte arvore binária:
Percorrendo em ordem:
(esquerda, raiz, direita)
jeba dc ihf g
Arvore Binária

19. 19
Inserção de itens
A inserção começa com a chave sendo atribuida a raiz, logo após a
função começa com uma busca, a-partir da raiz, comparando a chave
com o valor da raiz. Se a chave é menor ou igual do que a raiz, ela
é introduzida num novo nó a esquerda da raiz, ou na direita caso a
chave seja maior que a raiz, e assim sucessivamente, item a item, os
nós são criados.
Exemplo:
Itens a serem adicionados:
25, 11, 42, 6, 19, 37 e 14

20. 20
Remoção de itens
O processo de exclusão de um nó é o mais complexo. Para excluir um
nó de uma árvore binária, deve-se considerar três casos distintos:
Remoção da folha
A exclusão de um nó que se encontra no fim da árvore, isto é, na folha, é o caso
mais simples de exclusão. Basta remover o nó da árvore
Remoção de um nó com “filho”
Caso o nó que será excluído tenha um único "filho", o "avô" herda o "filho".
Remoção de um nó com dois “filhos”
Se o nó a ser excluído tiver dois "filhos", o processo de exclusão poderá operar de
duas maneiras diferentes:
 Substituir o valor do nó a ser retirado pelo valor sucessor (o nó mais à
esquerda da sub-árvore direita).
 Substituir o valor do nó a ser retirado pelo valor antecessor (o nó mais à direita
da sub-árvore esquerda).

21. 21
Remoção de itens
Remoção da folha
A exclusão de um nó que se encontra no fim da árvore, isto é, na folha, é o caso
mais simples de exclusão. Basta remover o nó da árvore

22. 22
Remoção de um nó com “filho”
Caso o nó que será excluído tenha um único "filho", o "avô" herda o "filho".
Remoção de itens

23. 23
Remoção de um nó com dois “filhos”
Se o nó a ser excluído tiver dois "filhos", o processo de exclusão poderá operar de
duas maneiras diferentes:
Substituir o valor do nó a ser retirado pelo valor sucessor (o nó mais à esquerda da
sub-árvore direita).
Remoção de itens

24. 24
Atividades
1. Uma sub-árvore de uma árvore binária sempre tem
(a) Uma raiz que é um filho da raiz da árvore principal
(b) Uma raiz não conectada a raiz da árvore principal
(c) Menos Nós que a árvore principal
(d) Uma irmã com mesmo número de Nós
2. Verdadeiro ou falso:
(a) Eliminar um Nó com um filho de uma árvore binária de busca envolve
encontrar o sucessor desse Nó.
(b) Nem todas as árvores são binárias.
(c) Uma árvore não balanceada é uma árvore na qual a raiz ou algum
outro Nó tenha muito mais filhos à esquerda do que filhos à direita ou
vice-versa.

25. 25
Atividades
3. Desenhe uma arvore binária usando a seguinte sequencia
de dados de entrada:
(a) 25, 11, 42, 6, 19, 37 e 14
(b) 11, 22, 33, 44, -11, -33 e -22
(c) 14, 4, 15, 3, 9, 13, 18, 7, 11, 16, 20, 5, 17, 4 e 5
Responda: Quantas folhas, nós e qual a altura das arvores (a), (b) e (c).
Escreva a arvore (b) e (c) em pré-ordem e pós-ordem.
Desenhe as arvores (a), (b) e (c) depois da inserção do nó 21 e da
remoção do nó 11 para as arvores (a) e (b) e nó 18 para arvore (c).