Baixado 373 vezes
![Busca
• Semelhante ao da árvore de pesquisa binária;
– Em cada nó interno
• Se x = k[i], retorna
• Se k[i-1] < x < k[i], procurar no filho f[i]
– Folha
• Se encontrou, retorna
– Não encontrou? Retorna null
Árvore B de Ordem 2
Árvore B](https://image.slidesharecdn.com/apresentacao-b-tree-2-120609065110-phpapp02/85/Apresentacao-sobre-Arvores-B-14-320.jpg)
Carregado porThiago Colares
Apresentação sobre Árvores B
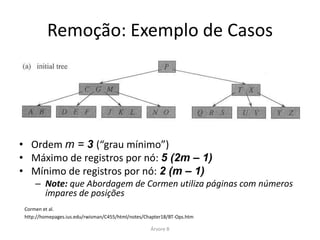
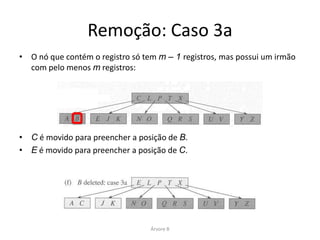
O documento apresenta a árvore B, uma estrutura de dados balanceada desenvolvida para acessar dados em armazenamento secundário, como discos. A árvore B minimiza acessos ao disco, permitindo um armazenamento eficiente e operações de busca, inserção e remoção de dados. Ele também descreve como a árvore B lida com a divisão de nós e garantias de balanceamento durante essas operações.
Mais conteúdo relacionado
![EDII14 [2012.1] Árvores B e B+](https://cdn.slidesharecdn.com/ss_thumbnails/edii142012-1-rvoresbeb-121020161700-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Semelhante a Apresentação sobre Árvores B
Apresentação sobre Árvores B
- 1. Árvores B Somos nós: Fernando Cerqueira, Jarbas Menezes Jr, Jailson Brito, Rafael Ávila, Thiago Colares e Vagner Amaral. Árvore B
- 2. Origem da ÁrvoreB • Criada por Bayer e McCreight, 1972; • Desenvolvida no Boeing Scientific Research Labs; • Origem do “B” é desconhecida. Hipóteses: – Boeing Scientific Research Labs; – Bayer-trees Árvore B
- 3. Caracterização da ÁrvoreB • Árvores de pesquisa balanceadas; • Projetadas para acessar dados em memória secundária; – Como discos ou outros dispositivos de armezenamento secundário de acesso direto. • Muito utilizadas em SGBDs – relacionais ou não Árvore B
- 4. Caracterização da ÁrvoreB • Objetivo: minimizar o número de acessos ao disco • Como? Maximizando o número de filhos de um nó, que pode chegar aos milhares. – Número de filhos é determinada pela ordem da árvore Árvore B
- 5. Exemplo de Aplicação: Acessar informações no disco rídigo. Árvore B
- 6. Discos • Tecnologia barata; •Alta capacidade armazenamento; • Informações armazenadas em trilhas; • Trilhas são divididas em em setores; • Aplicações sempre acessam o disco em unidades de blocos: (A) Trilha • Exemplo: 1kb a 8kb; (B) Setor geométrico • Acesso ao disco é (C) Setor de trilha muito custoso. (D) Blocos de alocação Árvore B
- 7. Problemas • Muito maislentos do que a memória principal; • Acesso fica custoso • Quantidade de dados manipulados não cabe na memória principal; (A) Trilha (B) Setor geométrico (C) Setor de trilha (D) Blocos de alocação Árvore B
- 8. Solução com ÁrvoreB • Uma árvore-B com grau 1001 e altura 2; • Pode armazenar mais de um bilhão de chaves; • O nó raiz permanentemente na memória principal; • No máximo dois acessos são necessários para ler qualquer chave! © 2001 Cormen et al. Árvore B
- 9. Solução com ÁrvoreB • Algoritmos só precisam um número constante de bloco na memória por vez; • O tamanho da memória principal não afeta o tamanho da Árvore-B que pode ser tratada; • O nó de uma Árvore-B é normalmente tão grande quando uma página de disco inteira; – Para evitar reads e writes do disco, que praticamente determinam o tempo de execução Árvore B
- 10. Definição • Em umaÁrvore B de ordem m temos que: – Cada página contém: • No mínimo m registros e m+1 descendentes • No máximo 2m registros e 2m+1 descendentes – Exceto a página raiz: • No mínimo 1 registro e 2 descendentes Árvore B
- 11. Exemplo • Árvore Bde ordem 2 • Cada página deve conter: • No mínimo 2 registros e 2+1 descendentes • No máximo 2 x 2 registros e 2 x 2 +1 descendentes – Exceto a página raiz: • No mínimo 1 registro e 2 descendentes Árvore B
- 12. Operações Árvore B
- 13. Inicialização • Um nóvazio é alocado no disco; • O nó é gravado no disco – não é executada nenhuma operação de leitura Árvore B
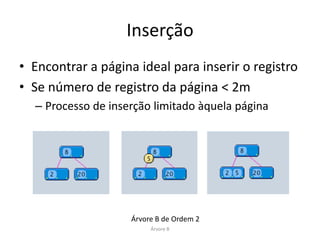
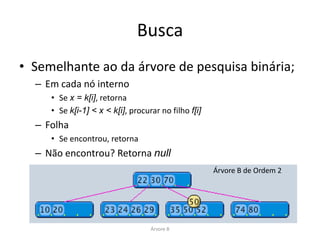
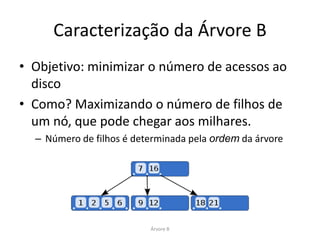
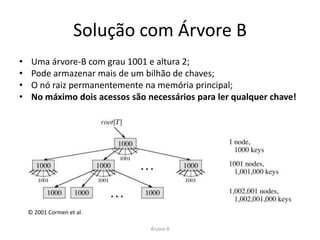
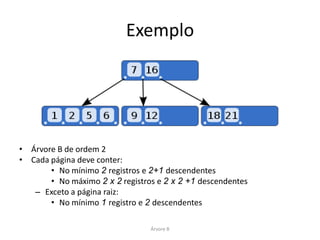
- 14. Busca • Semelhante aoda árvore de pesquisa binária; – Em cada nó interno • Se x = k[i], retorna • Se k[i-1] < x < k[i], procurar no filho f[i] – Folha • Se encontrou, retorna – Não encontrou? Retorna null Árvore B de Ordem 2 Árvore B
- 15. Inserção • Encontrar apágina ideal para inserir o registro • Se número de registro da página < 2m – Processo de inserção limitado àquela página Árvore B de Ordem 2 Árvore B
- 16. Inserção • Se númerode registro da página ≥ 2m – Após inserção, página é dividida – Registro do meio sobe para o nó pai – Demais registros são distribuídas igualmente entre os nós resultantes da divisão Árvore B de Ordem 2 Árvore B
- 17. Inserção • Se númerode registro da página escolhida e do pai foram ambos ≥ 2m Árvore B
- 18. Remoção • Registro podeser removido de qualquer nó; • A remoção deve assegurar que nenhum nó ficará com menos que m – 1 registros • O algoritimo desce a árvore B uma única vez (sem subir de volta) – Exceção: quando não envolver leitura e escrita em disco • A remoção de um registro interno (não-folha) é recursiva. Árvore B
- 19. Remoção: Exemplo deCasos • Ordem m = 3 (“grau mínimo”) • Máximo de registros por nó: 5 (2m – 1) • Mínimo de registros por nó: 2 (m – 1) Cormen at al. http://homepages.ius.edu/rwisman/C455/html/notes/Chapter18/BT-Ops.htm Árvore B
- 20. Remoção: Caso 1 • A chave está em um nó folha que contém pelo menos m registros. • Caso mais simples, eliminação de uma folha Árvore B
- 21. Remoção: Caso 2a/ 2b • Chave está em nó interno. Nó do predecessor tem pelo menos m registros. • O predecessor L de M é movido para cima, no lugar de M. Árvore B
- 22. Remoção: Caso 2c •Chave está em nó interno e filhos tem apenas m-1 registros. • G é empurrado para baixo, forma-se D E G J K • Então G é eliminado recursivamente da folha; Árvore B
- 23. Remoção: Caso 3b •Chave que contém D é folha; • Mas a recursão não pode descer até D, pois o nó C L só tem dois registros; – Mínimo • Logo, o nó C Lprecisa ser reorganizado. Árvore B
- 24. Remoção: Caso 3b • Então P é empurrado para baixo, e intercalado com C L e T X; • Forma-se C L P T X. D é eliminado (como no Caso 1); • Em seguida, a raiz é eliminada e a árvore encolhe uma unidade em altura. Árvore B
- 25. Remoção: Caso 3a •O nó que contém o registro só tem m – 1 registros, mas possui um irmão com pelo menos m registros: • C é movido para preencher a posição de B. • E é movido para preencher a posição de C. Árvore B
- 26. Exercício Árvore B
- 27. Exercícios • Escolher umcampo do registro Music e implementar um outro índice, mantendo o índice atual; • Deve ser possível fazer Pesquisa e Remoção usando qualquer um dos índices. • Extra: Escolher o novo índice em tempo de execução Árvore B
Notas do Editor
- #4 Antes de formalizarmos o conceito de árvores-B, vamos examinar porque estruturas de dadosarmazenadas em disco possuem característicasdiferentes das armazenadas na memóriaprincipal.
- #5 Exemplo de árvore tree. Note que
- #8 Muitasvezesdemoramais tempoparaacessarumapágina de informações e ler a leitura do disco que o tempo necessáriopara o computadorexaminar as informaçõesObservamostambémque o tempo de acessoao disco nãoéconstante – depende da distância entre a trilhaatual e a trilhadesejada
- #9 Explicação do pq: https://docs.google.com/viewer?a=v&q=cache:Y_pOhDF4fOUJ:www.dsc.ufcg.edu.br/~baptista/cursos/EDados/Unidade4Btree.doc+&hl=pt-BR&gl=br&pid=bl&srcid=ADGEESgx1CTemnjsTCeKPsdCJSnnDF4d9THiO7k8nyMSGVkQoPhpOVPhWZvrRWFJ_fXryolYlxDFxP9TCXIsb6lZWmM4-QMqGGsUqJ2-7qTjhmlYpZgZ9tPHFZYJYqCtuhmczF2Obsn0&sig=AHIEtbTbPsYggPwj4runBcv5Z58TyCTxVg•Já que os algoritmos de manipulação deárvores-B só precisam de um número constantede blocos na memória de cada vez, o tamanhoda memória principal não afeta o tamanho daárvore-B que pode ser tratada
- #10 Algoritmos de manipulação de Árvores-B só precisam de um número constante de blocos na memória de cada vez;
- #11 Algunsautores,comoZiviani, nãoregistrigem m ≥ 2, mas utilizamoslimitessubtraídos de 1
- #12 Nemsempreépossívelrespeitarestaregra?
- #15 Binária: toma-sedecisão de remificaçãobináriaÁrvore-b: toma-se decisão de ramificação número-de-registros-do-nó+1
- #18 Paiédivididoemdois, e registro do meiovaipara um nóacima.
- #19 Deleting from an internal node is recursive, meaning that child nodes must be adjusted down to a leaf node since there is one less key.
- #22 Encontre o predecessor (valor anterior) da registro (númeromais alto nasubárvoreàesquerda)Substitua o precedessorpelachaveque se quer remover (façaistorecursivamente) (Necessary since one less key in predecessor node. (mm?))Pare nafolha
- #23 Merge G com todososregistros dos filhos. Géempurradoparabaixo, forma-se D E G J K.NóperdeG e o ponteiropara um dos filhosO filho restante(D E G J K) contém 2m – 1 registros.Então G éeliminadorecursivamente da folha;
- #24 CASO 3 GERAL:http://homepages.ius.edu/rwisman/C455/html/notes/Chapter18/BT-Ops.htm (baseado no Cormen)If he key k is not present in internal node x, determine root x.ci of the appopriate child subtree that must contain k, if k is in the tree at all.Ifx.ci has only t-1 keys, execute steps 3a or 3b as necessary to guarantee descent to a node with at least t keys.Then finish by recursing on the appropriate x.c
- #26 O nóquecontém o registrosó tem m – 1 chaves, mas possui um irmão com pelomenosmregistros:Give x.ci an extra key by moving a key from x down into x.ciMoving a key from x.ci immediate left or right sibling up into x and moving the appropriate child pointer from the sibling into x.ci.