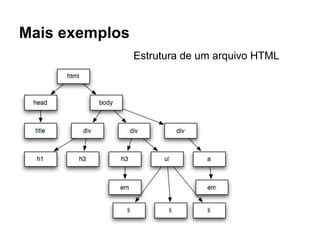
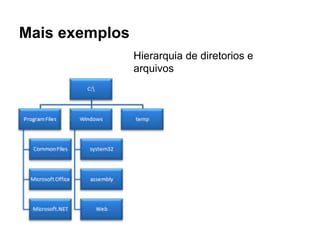
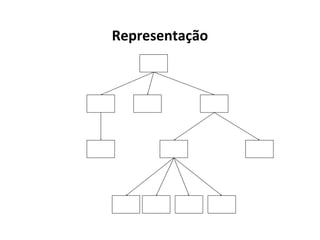
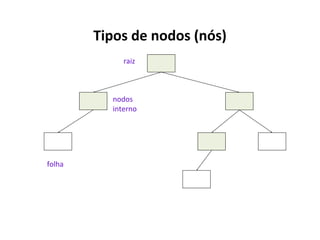
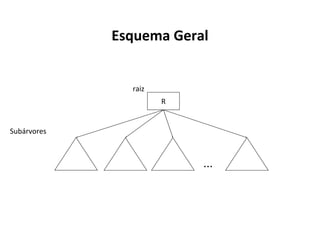
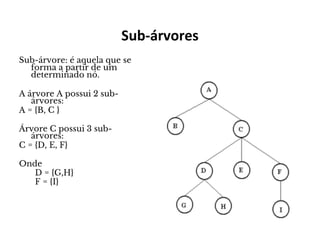
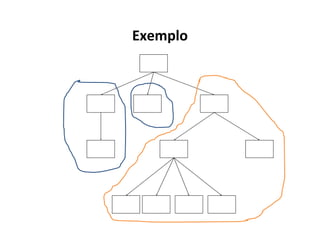
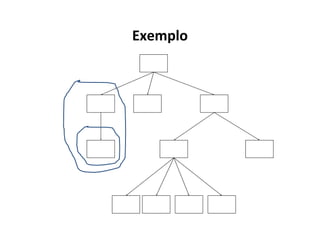
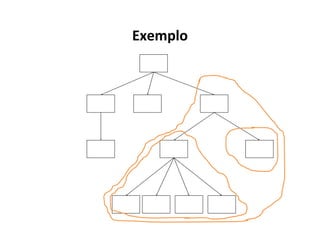
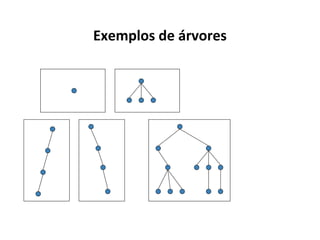
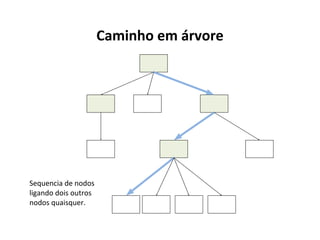
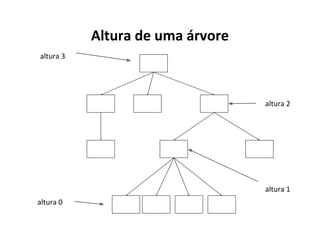
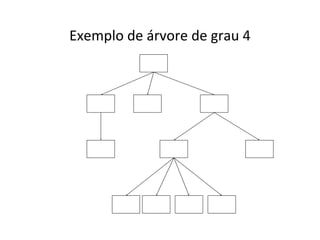
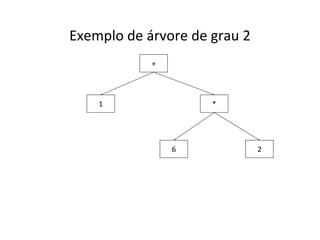
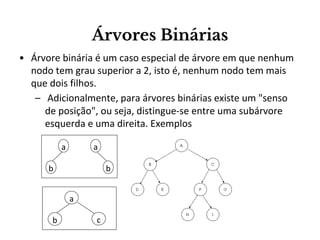
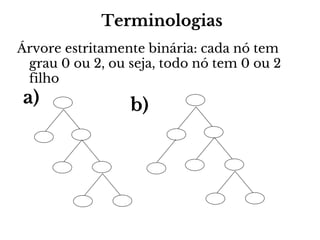
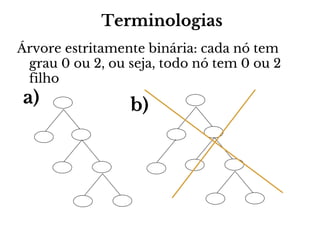
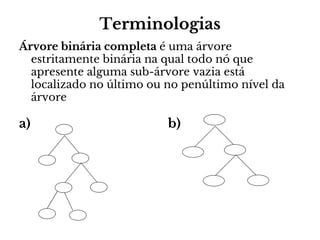
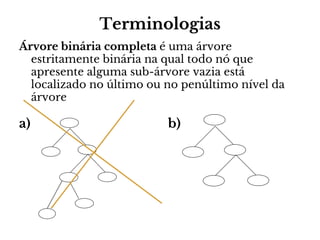
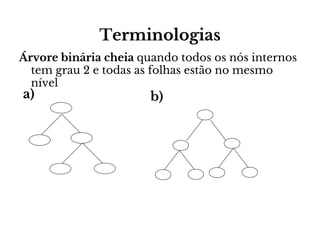
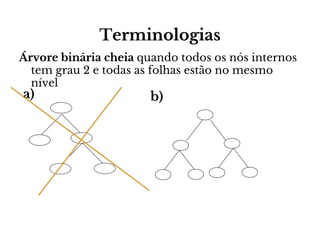
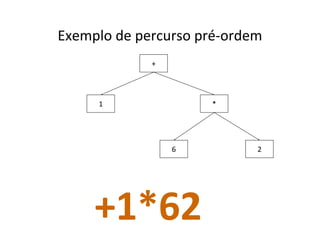
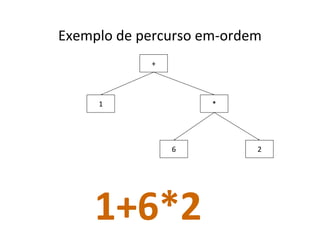
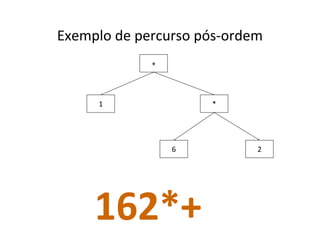
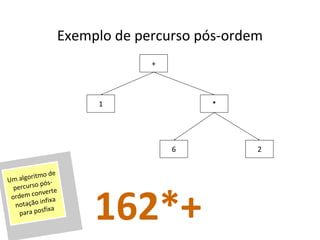
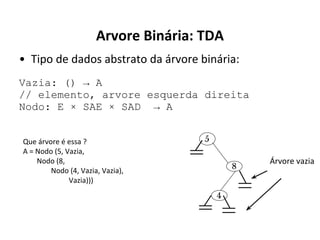
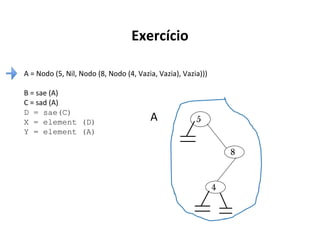
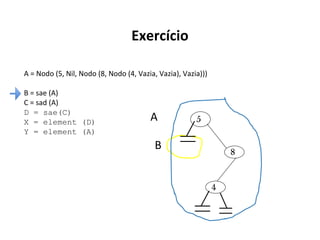
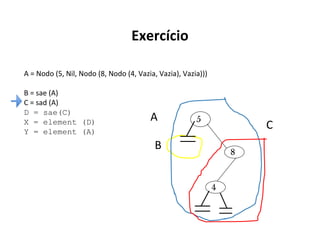
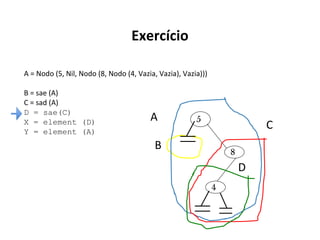
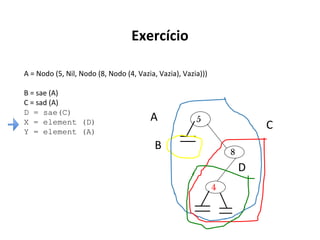
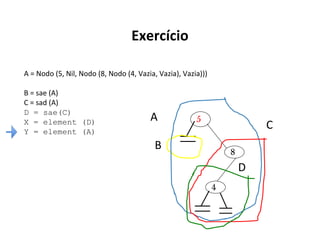
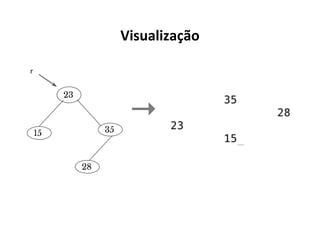
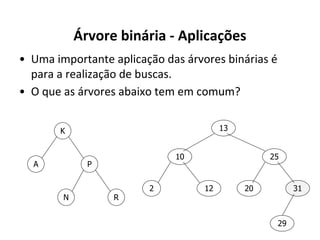
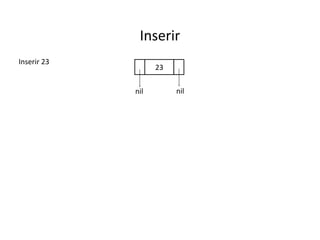
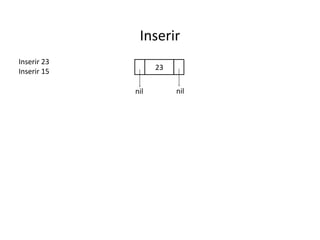
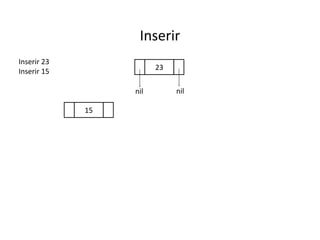
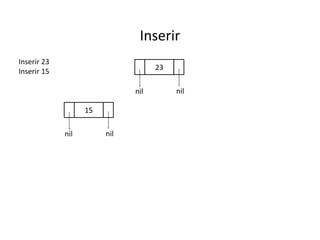
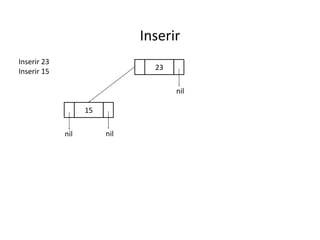
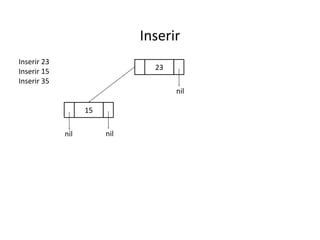
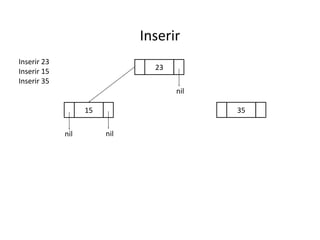
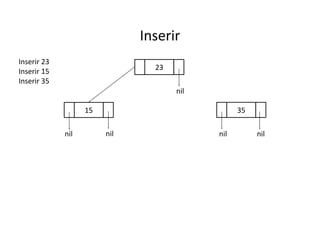
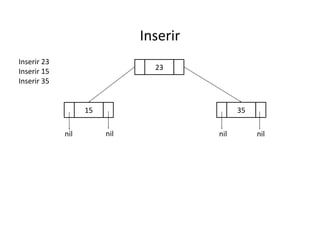
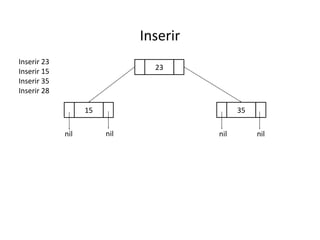
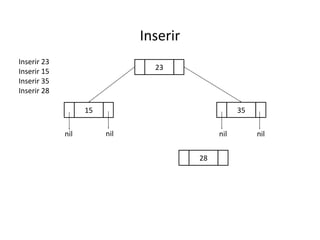
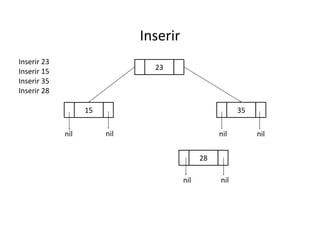
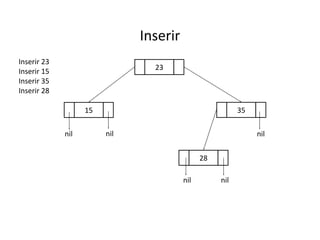
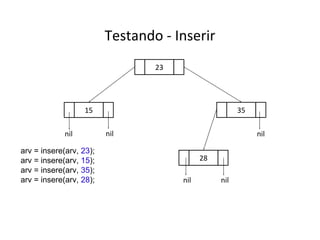
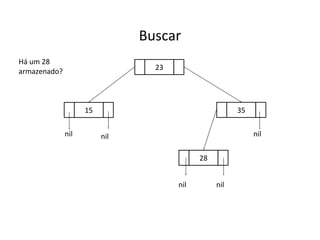
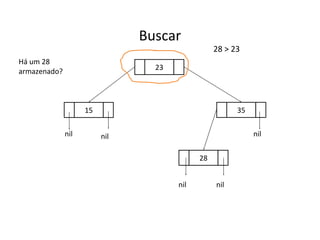
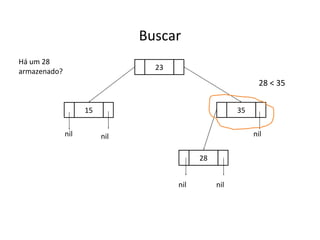
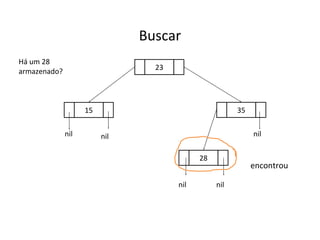
O documento apresenta conceitos sobre árvores binárias. Resume que árvores binárias são estruturas de dados não lineares e hierárquicas onde cada nó pode ter no máximo dois filhos, denominados subárvore esquerda e direita. Além disso, explica termos como raiz, folhas, altura da árvore e operações de percurso como pré-ordem, em-ordem e pós-ordem.

1. Árvores - Conceitos e
binária
Prof: Sergio Souza Costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
http://www.slideshare.net/skosta/presentations?order=popular
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta

3. Árvores
Conceitos

4. Árvores
• Estrutura não linear
• Hieráquica
• Recursiva

5. Árvores
• Nodos interligados de maneira hierárquica
• Nodo superior (raiz / pai), apontando para os seus
nodos filhos (folhas / filho).

6. Analogia no mundo real
• Estrutura organizacional de uma empresa
– Departamentos, setores, seções, etc.
• Organização de um livro
– Partes, capítulos, seções, parágrafos

7. Mais exemplos
Estrutura de um arquivo HTML

8. Mais exemplos
Hierarquia de diretorios e
arquivos

9. Representação

10. Tipos de nodos (nós)
raiz
nodos
interno
folha

11. Definições
• Raíz: um nodo sem pai
• Nodo: um elemento qualquer
• Folha: um nó que possui grau zero, ou seja, suas
subárvores são vázia.
• Sub-árvore: formada por todos os nodos filhos a
partir de um nodo qualquer

12. Definição geral
• Um nodo sem filhos e sem pai é uma árvore vazia.
• Um nodo com qualquer número de subárvores
descendentes é uma árvore

13. Esquema Geral
raiz
R
Subárvores
...

14. Sub-árvores
Sub-árvore: é aquela que se
forma a partir de um
determinado nó.
A árvore A possui 2 subárvores:
A = {B, C }
Árvore C possui 3 subárvores:
C = {D, E, F}
Onde
D = {G,H}
F = {I}

15. Exemplo

16. Exemplo

17. Exemplo

18. Exemplos de árvores

19. Caminho em árvore
Sequencia de nodos
ligando dois outros
nodos quaisquer.

20. Caminho em árvore
• Nota: Só existe um caminho desde a raiz até um
determinado nó.

21. Altura de uma árvore
• Altura é o tamanho do maior caminho desde a raiz
até uma folha

22. Altura de uma árvore
altura 3
altura 2
altura 1
altura 0

23. Altura de uma árvore
• A altura da raiz é 0.
• Por definição, a altura de uma árvore vazia é -1.

24. Grau de uma árvore
• O grau de uma árvore é dado pela quantidade de
descendentes permitido a cada nodo.

25. Exemplo de árvore de grau 4

26. Exemplo de árvore de grau 2
+
1
*
6
2

27. Árvores
Binárias

28. Árvores Binárias
• Árvore binária é um caso especial de árvore em que nenhum
nodo tem grau superior a 2, isto é, nenhum nodo tem mais
que dois filhos.
– Adicionalmente, para árvores binárias existe um "senso
de posição", ou seja, distingue-se entre uma subárvore
esquerda e uma direita. Exemplos
a
a
b
b
a
b
c

29. Árvores Binárias
• Uma árvore binária é uma árvore que
pode ser nula, ou então tem as seguintes
características:
– existe um nodo especial denominado raiz;
– os demais nodos são particionados em T1, T2
estruturas disjuntas de árvores binárias;
– T1 é denominada subárvore esquerda e T2,
subárvore direita da raiz.

30. Árvores Binárias
• Uma árvore binária é uma árvore que
pode ser nula, ou então tem as seguintes
características:
– existe um nodo especial denominado raiz;
– os demais nodos são particionados em T1, T2
estruturas disjuntas de árvores binárias;
– T1 é denominada subárvore esquerda e T2,
subárvore direitaem a raiz.
da
Observ
na
sividade
recur
ição
sua defin

31. Exemplo
Chaves de campeonatos

32. ÁRVORE BINÁRIA - EXEMPLO
Chaves de campeonatos

33. Terminologias
Árvore estritamente binária: cada nó tem
grau 0 ou 2, ou seja, todo nó tem 0 ou 2
filho
a)
b)

34. Terminologias
Árvore estritamente binária: cada nó tem
grau 0 ou 2, ou seja, todo nó tem 0 ou 2
filho
a)
b)

35. Terminologias
Árvore binária completa é uma árvore
estritamente binária na qual todo nó que
apresente alguma sub-árvore vazia está
localizado no último ou no penúltimo nível da
árvore
a)
b)

36. Terminologias
Árvore binária completa é uma árvore
estritamente binária na qual todo nó que
apresente alguma sub-árvore vazia está
localizado no último ou no penúltimo nível da
árvore
a)
b)

37. Terminologias
Árvore binária cheia quando todos os nós internos
tem grau 2 e todas as folhas estão no mesmo
nível
a)
b)

38. Terminologias
Árvore binária cheia quando todos os nós internos
tem grau 2 e todas as folhas estão no mesmo
nível
a)
b)

39. Percurso em Árvores

40. Percurso em árvore binária
• Pré-ordem: visita a raiz, depois a sub-árvore da
esquerda e depois direita.
• Em-ordem: visita a sub-árvore esquerda, depois a
raiz, e finalmente a sub-árvore direita.
• Pós-ordem: visita a sub-árvore da esquerda, depois
da direita e por ultimo imprime a raiz.

41. Exemplo de percurso pré-ordem
+
1
*
6
+1*62
2

42. Exemplo de percurso em-ordem
+
1
*
6
1+6*2
2

43. Exemplo de percurso pós-ordem
+
1
*
6
162*+
2

44. Exemplo de percurso pós-ordem
+
1
*
6
o de
algoritm
Um
pósercurso
p
nverte
rdem co
o
infixa
notação
fixa
para pos
162*+
2

45. Arvore Binária: TDA
• Tipo de dados abstrato da árvore binária:
Vazia: () → A
// elemento, arvore esquerda direita
Nodo: E × SAE × SAD → A

46. Arvore Binária: TDA
• Tipo de dados abstrato da árvore binária:
Vazia: () → A
// elemento, arvore esquerda direita
Nodo: E × SAE × SAD → A
Que árvore é essa ?
A = Nodo (5, Vazia,
Nodo (8,
Nodo (4, Vazia, Vazia),
Vazia)))

47. Arvore Binária: TDA
• Tipo de dados abstrato da árvore binária:
Vazia: () → A
// elemento, arvore esquerda direita
Nodo: E × SAE × SAD → A
Que árvore é essa ?
A = Nodo (5, Vazia,
Nodo (8,
Nodo (4, Vazia, Vazia),
Vazia)))
5
8
4
Árvore vazia

48. Arvore Binária: TDA
• Operações acessoras:
sae:: A → A // retorna a subarvore esquerda
sad:: A → A // retorna a subarvore direita
element :: A → E // retorno o elemento do nó

49. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)

50. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
8
4

51. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
B
8
4

52. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
C
B
8
4

53. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
C
B
8
D
4

54. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
C
B
8
D
4

55. Exercício
A = Nodo (5, Nil, Nodo (8, Nodo (4, Vazia, Vazia), Vazia)))
B = sae (A)
C = sad (A)
D = sae(C)
X = element (D)
Y = element (A)
A
5
C
B
8
D
4

56. Exercícios resolvidos
• Ainda sem codificar em C a nossa árvore, faremos os
seguintes exercícios.
• Podem fazer no papel ou bloco de notas, não
precisem compilar (apenas mentalmente).
• Usando recursividade e apenas as quatro operações
vistas anteriormente, vamos fazer os seguintes
exercícios.

57. Exercícios resolvidos
1. Some os valores dos elementos de uma arvore binária
int soma (ArvBin *a) {
if (a == Vazia())
return 0;
}

58. Exercícios resolvidos
1. Some os valores dos elementos de uma arvore binária
int soma (ArvBin *a) {
if (a == Vazia())
return 0;
return elem(a)
+ soma (sae(a))
+ soma (sad(a));
}

59. Exercícios resolvidos
1. Retorne a altura de uma árvore binaria. Onde a Altura é
o tamanho do maior caminho desde a raiz até uma folha.
Por definição, a altura de uma árvore vazia é -1.
int altura(ArvBin *a) {
}

60. Exercícios resolvidos
1. Retorne a altura de uma árvore binaria. Onde a Altura é
o tamanho do maior caminho desde a raiz até uma folha.
Por definição, a altura de uma árvore vazia é -1.
int altura(ArvBin *a) {
if (a == Vazia())
return -1;
}

61. Exercícios resolvidos
1. Retorne a altura de uma árvore binaria. Onde a Altura é
o tamanho do maior caminho desde a raiz até uma folha.
Por definição, a altura de uma árvore vazia é -1.
int altura(ArvBin *a) {
if (a == Vazia())
return -1;
return maior(
altura (sae (a)),
altura (sad (a))
) + 1;
}

62. Exercícios resolvidos
1. Retorne a altura de uma árvore binaria. Onde a Altura é
o tamanho do maior caminho desde a raiz até uma folha.
Por definição, a altura de uma árvore vazia é -1.
int altura(ArvBin *a) {
if (a == Vazia())
return -1;
return maior(
altura (sae (a)),
altura (sad (a))
) + 1;
}

63. Exercícios resolvidos
1. Retorne a altura de uma árvore binaria. Onde a Altura é
o tamanho do maior caminho desde a raiz até uma folha.
Por definição, a altura de uma árvore vazia é -1.
int maior (int v1, int v2) {
int altura(ArvBin *a) {
if
if (a == Vazia())(v1 > v2)
return -1; return v1 ;
return maior(else return v2;
}
altura (sae (a)),
altura (sad (a))
) + 1;
}

64. Codificação
• A árvore binária é representado pela estrutura
abaixo.
typedef struct ArvBin {
int elem;
struct ArvBin *sae;
struct ArvBin *sad;
} ArvBin;

65. Codificação
• Operações construtoras
ArvBin* Vazia () {
return NULL;
}
ArvBin* Nodo (int elem, ArvBin* sae, ArvBin* sad ) {
ArvBin* a = (ArvBin*)malloc (sizeof (ArvBin));
a->elem = elem;
a->sad = sad;
a->sae = sae;
return a;
}

66. Codificação
• Operações construtoras
ArvBin* Vazia () {
return NULL;
}
ArvBin* Nodo (int elem, ArvBin* sae, ArvBin* sad ) {
ArvBin* a = (ArvBin*)malloc (sizeof (ArvBin));
a->elem = elem;
a->sad = sad;
a->sae = sae;
return a;
}

67. Codificação
• Operações construtoras
ArvBin* Vazia () {
return NULL;
}
ArvBin* Nodo (int elem, ArvBin* sae, ArvBin* sad ) {
ArvBin* a = (ArvBin*)malloc (sizeof (ArvBin));
a->elem = elem;
a->sad = sad;
a->sae = sae;
return a;
}

68. Codificação
• Operações construtoras
ArvBin* Vazia () {
return NULL;
}
ArvBin* Nodo (int elem, ArvBin* sae, ArvBin* sad ) {
ArvBin* a = (ArvBin*)malloc (sizeof (ArvBin));
a->elem = elem;
a->sad = sad;
a->sae = sae;
return a;
}

69. Codificação
• Operações construtoras
ArvBin* Vazia () {
return NULL;
}
ArvBin* Nodo (int elem, ArvBin* sae, ArvBin* sad ) {
ArvBin* a = (ArvBin*)malloc (sizeof (ArvBin));
a->elem = elem;
a->sad = sad;
a->sae = sae;
return a;
}

70. Codificação
• Operações retornar os atributos da árvore.
int elem (ArvBin* b) { return b->elem;}
ArvBin* sae (ArvBin* b) { return b->sae;}
ArvBin* sad (ArvBin* b) { return b->sad;}

71. Codificação
• Código para visualizar uma árvore binária “deitada”
void mostra (ArvBin *a, int n) {
if (a) {
int i;
mostra (sad(a), n+1);
for (i = 0; i < n; i++) printf ("t");
printf ("%dn", elem(a));
mostra (sae(a), n+1);
}
}

72. Visualização
r
23
35
15
28

73. Árvore binária - Aplicações
• Uma importante aplicação das árvores binárias é
para a realização de buscas.
• O que as árvores abaixo tem em comum?
13
K
A
10
P
2
N
25
12
20
31
R
29

74. Árvore Binária De Busca
• Operações básicas
– Insere elemento
– Busca
– Remoção

75. INSERÇÃO
• Para adicionar um elemento x
– Se a árvore estiver vazia, adicione um novo
nó contendo o elemento x
– Se a raiz é maior que x então insira x na
subárvore esquerda, caso contrário
– insira x na subárvore direita

76. Inserir
Inserir 23

77. Inserir
Inserir 23
23

78. Inserir
Inserir 23
23
nil
nil

79. Inserir
Inserir 23
Inserir 15
23
nil
nil

80. Inserir
Inserir 23
Inserir 15
23
nil
15
nil

81. Inserir
Inserir 23
Inserir 15
23
nil
15
nil
nil
nil

82. Inserir
Inserir 23
Inserir 15
23
nil
15
nil
nil

83. Inserir
Inserir 23
Inserir 15
Inserir 35
23
nil
15
nil
nil

84. Inserir
Inserir 23
Inserir 15
Inserir 35
23
nil
35
15
nil
nil

85. Inserir
Inserir 23
Inserir 15
Inserir 35
23
nil
35
15
nil
nil
nil
nil

86. Inserir
Inserir 23
Inserir 15
Inserir 35
23
35
15
nil
nil
nil
nil

87. Inserir
Inserir 23
Inserir 15
Inserir 35
Inserir 28
23
35
15
nil
nil
nil
nil

88. Inserir
Inserir 23
Inserir 15
Inserir 35
Inserir 28
23
35
15
nil
nil
nil
28
nil

89. Inserir
Inserir 23
Inserir 15
Inserir 35
Inserir 28
23
35
15
nil
nil
nil
28
nil
nil
nil

90. Inserir
Inserir 23
Inserir 15
Inserir 35
Inserir 28
23
35
15
nil
nil
nil
28
nil
nil

91. Inserir - Código
ArvBin *insere (ArvBin *r, int x) {
if (r == NULL)
r = Nodo (x, NULL, NULL);
else if (x < elem(r) )
r->sae = insere(sae(r), x ) ;
else
r->sad = insere(sad(r), x ) ;
return r;
}

92. Testando - Inserir
23
35
15
nil
arv = insere(arv, 23);
arv = insere(arv, 15);
arv = insere(arv, 35);
arv = insere(arv, 28);
nil
nil
28
nil
nil

93. Busca
• Para encontrar um elemento x
– Se x é a raiz então x foi encontrado, caso
contrário
– Se x é menor que a raiz então procure x na
sub-árvore esquerda, caso contrário
– Procure x na sub-árvore direita de
– Se a árvore é vazia então a busca falha

94. Buscar
Há um 28
armazenado?
23
35
15
nil
nil
nil
28
nil
nil

95. Buscar
28 > 23
Há um 28
armazenado?
23
35
15
nil
nil
nil
28
nil
nil

96. Buscar
Há um 28
armazenado?
23
28 < 35
35
15
nil
nil
nil
28
nil
nil

97. Buscar
Há um 28
armazenado?
23
35
15
nil
nil
nil
28
nil
encontrou
nil

98. Código - Buscar
ArvBin* busca (ArvBin *r, int x) {
if ((!r) || (elem(r) == x))
return r;
else {
if (elem(r) < x)
return busca(sad(r),x);
else
return busca(sae(r),x);
}
}
Parada: Achou o
elemento ou o
elemento não se
encontra na
arvore.