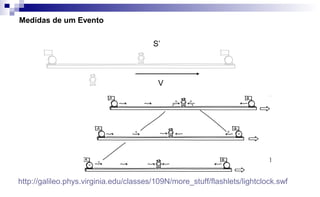
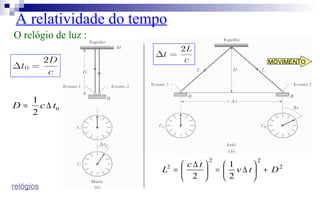
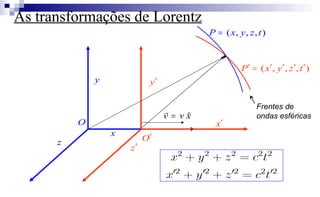
O documento apresenta um resumo sobre um minicurso de introdução à relatividade especial, teoria desenvolvida por Albert Einstein. O minicurso irá abordar conceitos como cinemática relativística, relatividade do tempo e comprimento, e as equações de transformação de Lorentz.