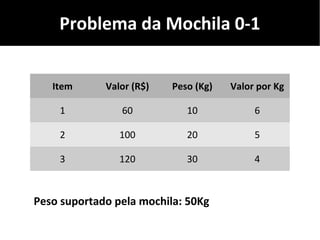
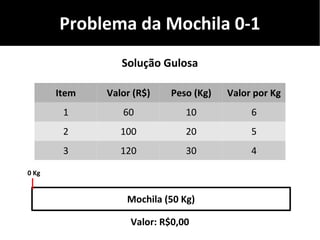
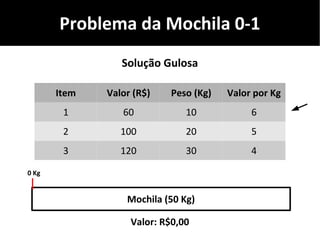
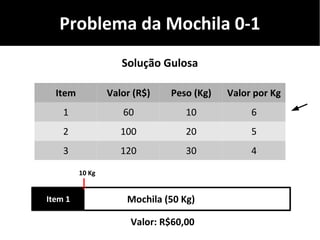
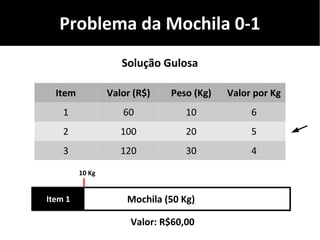
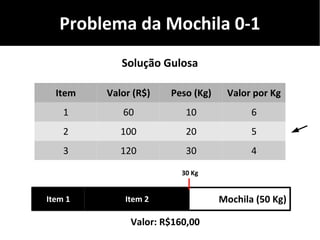
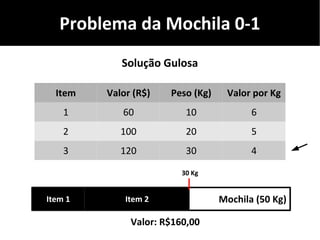
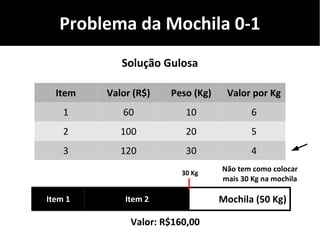
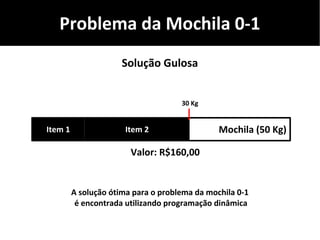
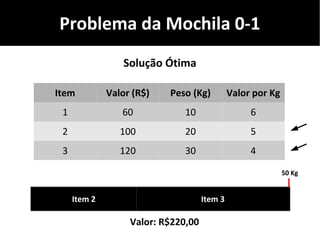
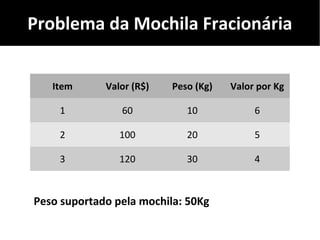
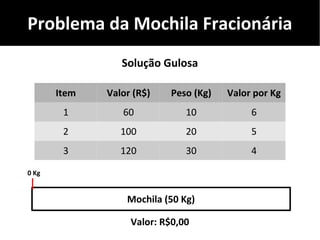
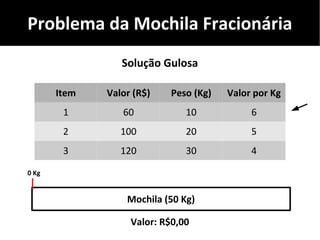
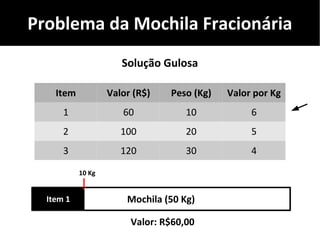
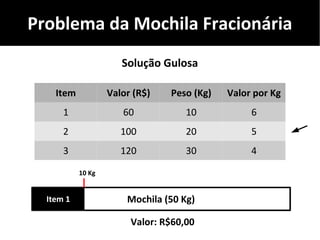
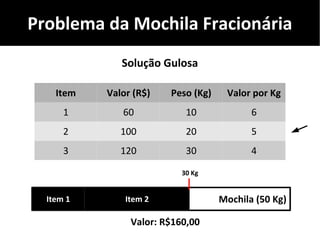
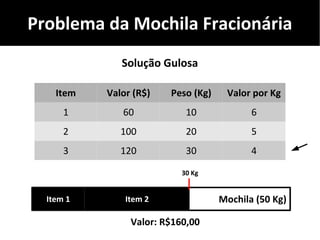
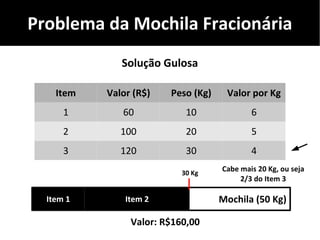
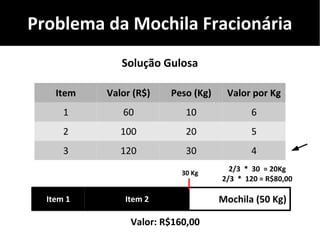
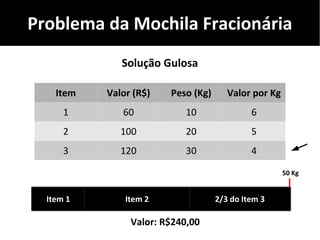
O documento discute algoritmos gulosos e seu uso para resolver problemas de otimização, como o problema da mochila. Apresenta o conceito de algoritmos gulosos, características-chave e exemplos como o problema da mochila 0-1 e fracionária. Fornece detalhes sobre como aplicar uma abordagem gulosa para encontrar uma solução para esses problemas.

1. Luís Ovídio Viana Podestá
Fabiana Zioti
Vinícius Henrique Marangoni
Algoritmo Guloso

2. Roteiro
→ Introdução
→ Matróide
→ Problema da Mochila
→ Algoritmo da mochila em C++
→ Exercícios

3. Algoritmo
Algoritmo é uma sequência finita de
instruções bem definidas que devem ser
seguidas para resolver um problema ou
executar uma tarefa.

4. Otimização
Otimização em matemática, corresponde ao
estudo de problemas onde se busca minimizar ou
maximizar uma função.
As técnicas matemáticas de otimização visam
encontrar uma "solução ótima" para certo
problemas, ou seja, que resulte no melhor
desempenho possível do sistema.
Normalmente esses problemas são modelos da
realidade física, então inicialmente é necessário
construir um modelo matemático.

5. Algoritmo Guloso
Uma das estratégias para resolver
problemas de otimização são os algoritmos
gulosos ou paradigma guloso na
concepção de algoritmos.
Ele escolhe a melhor opção naquele
momento (melhor opção local), e assim
pretende chegar a melhor solução no todo
(global).

6. Características
● Algoritmos simples e de fácil implementação.
● Nem sempre conduz à soluções ótimas globais.
● Podem efetuar cálculos repetitivos.
● Um algoritmo guloso é "míope“.
● Nunca reconsideram decisões tomadas.

7. Matróide
Um Matróide é um par ordenado M = (S, I), satisfazendo as
seguintes condições:
1. S é um conjunto finito não vazio
2. I é uma família não vazia de subconjuntos de S, chamada de
subconjuntos independentes de S, tal que se B I∈ e A B⊆ então
A I∈ . Observe que o conjunto vazio deve ser necessariamente
um membro de I. Neste caso dizemos que I é hereditário
3. Se A I∈ , B I∈ e |A| < |B|, então existe algum elemento x (B-A)∈
tal que A U {x} I∈ .
Dizemos que M satisfez a propriedade de troca.

8. Problema da Mochila
Um ladrão que rouba uma loja encontra n itens, onde cada
item vale v reais e pesa p quilos. O ladrão deseja levar a carga
mais valiosa possível, mas consegue levar apenas W quilos em
sua mochila.
No problema da mochila 0-1, o ladrão deve levar itens
inteiros. Já no problema da mochila fracionária, o ladrão pode
levar frações de um item.
OBS: A solução gulosa para o problema da mochila 0-1 não
garante uma solução ótima.

9. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Peso suportado pela mochila: 50Kg

10. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$0,00
0 Kg

11. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$0,00
0 Kg

12. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$60,00
Item 1
10 Kg

13. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$60,00
10 Kg
Item 1

14. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
Item 2
30 Kg
Item 1

15. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
Item 2Item 1

16. Problema da Mochila 0-1
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
Não tem como colocar
mais 30 Kg na mochila
Item 2Item 1

17. Problema da Mochila 0-1
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
Item 2Item 1
A solução ótima para o problema da mochila 0-1
é encontrada utilizando programação dinâmica

18. Problema da Mochila 0-1
Solução Ótima
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Mochila (50 Kg)
Valor: R$220,00
50 Kg
Item 2 Item 3

19. Problema da Mochila Fracionária
● No problema da mochila fracionária, podemos fracionar um
item
● Por exemplo:
Cabe apenas mais 10 Kg na mochila e eu tenho um item
que pesa 100 Kg. Então eu posso fracionar o item de
forma a colocar apenas 10% de seu peso na mochila e
consequentemente colocar apenas 10% de seu valor

20. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Peso suportado pela mochila: 50Kg

21. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$0,00
0 Kg

22. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$0,00
0 Kg

23. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$60,00
Item 1
10 Kg

24. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$60,00
10 Kg
Item 1

25. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
Item 2
30 Kg
Item 1

26. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
Item 2Item 1

27. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
Cabe mais 20 Kg, ou seja
2/3 do Item 3
Item 2Item 1

28. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$160,00
30 Kg
2/3 * 30 = 20Kg
2/3 * 120 = R$80,00
Item 2Item 1

29. Problema da Mochila Fracionária
Item Valor (R$) Peso (Kg) Valor por Kg
1 60 10 6
2 100 20 5
3 120 30 4
Solução Gulosa
Mochila (50 Kg)
Valor: R$240,00
50 Kg
Item 2Item 1 2/3 do Item 3

30. Problema da Mochila Fracionária
Solução Gulosa → Ótima
Mochila (50 Kg)
Valor: R$240,00
50 Kg
Item 2Item 1 2/3 do Item 3

31. Algoritmo
Mochila.cpp

32. Gula vs Programação Dinâmica
Às vezes é difícil distinguir um algoritmo guloso de um
algoritmo de programação dinâmica. Algumas características que
podem ajudar são:
Guloso Programação Dinâmica
Alternativa mais promissora Explora todas as alternativas
É muito rápido Um tanto lento
Nunca se arrepende Pode se arrepender
Não tem garantia de solução ótima Tem garantia de solução ótima

33. Outros Algoritmos Gulosos
● Código de Huffman
● Algoritmo de Kruskal
(Árvore Geradora de Peso Mínimo - Grafos)
● Dijkstra (Caminho Mínimo - Grafos)