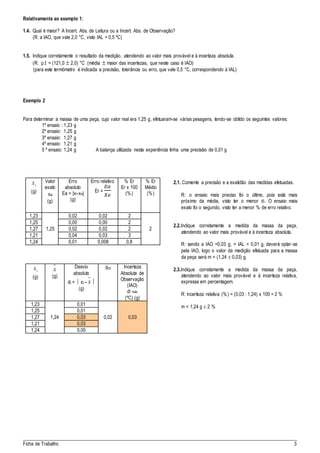
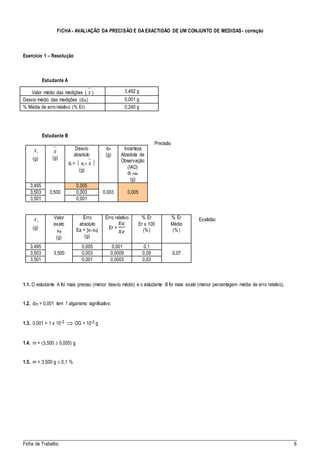
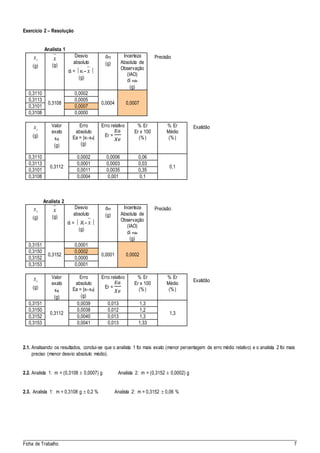
O documento descreve os conceitos de precisão e exatidão na avaliação de medidas experimentais, definindo cada um e explicando como calculá-los e avaliá-los. É fornecido um exemplo numérico para ilustrar o cálculo da exatidão e precisão de um conjunto de medidas do ponto de fusão de uma substância.

1. _____________________________________________________________________________________
Ficha de Trabalho 1
AVALIAÇÃO DA PRECISÃO E DA EXATIDÃO DE UM CONJUNTO DE MEDIDAS
Exatidão – é a proximidade entre os valores medidos para determinada grandeza e o valor verdadeiro dessa grandeza. Quanto mais
próximo do valor verdadeiro estiver o valor da medição, mais exata é a medida.
A exatidão é afetada pelos erros sistemáticos.
Quando se dispõe de dois ou mais conjuntos de medidas, efetuados por operadores diferentes, pode avaliar-se qual o operador que mais
se aproximou do valor verdadeiro (o mais exato). Para avaliar a exatidão, deve conhecer-se o valor real ou verdadeiro – xe. Seguidamente
constrói-se uma tabela e calcula-se
Ea – erro absoluto (Ea =| xi-xe|)
Er – erro relativo (Er = Ea / xe)
Er (%) – percentagem de erro relativo (% Er = Er x 100) → permite avaliar qual das medições (ou ensaios) foi mais exato. Será mais exato
o ensaio que possuir menor Ea ou menor Er. No caso de se ter dois ou mais conjuntos de medições efetuados por operadores
diferentes, o operador mais exato será aquele que apresentar menor % Er médio.
Precisão – traduz a concordância (proximidade) entre os valores de várias medições de uma mesma grandeza, isto é, traduz a
repetibilidade da medida. Quanto mais próximos uns dos outros estiverem os vários valores medidos, maior a precisão.
A precisão é afetada pelos erros aleatórios, ou acidentais ou fortuitos.
Para minimizar os erros na medição de uma grandeza, devem efetuar-se várias medições (ensaios)
Para avaliar a precisão de uma medição ou conjunto de medições efetuadas por operadores diferentes, é necessário calcular
x - média dos vários ensaios ou valor mais provável
n
xxxx
x n

...321
di – desvio absoluto (di = l xi- x l ) → permite avaliar qual das medições (ou ensaios) foi mais preciso. Será mais preciso o ensaio que
possuir menor di. No caso de se ter dois ou mais conjuntos de medições efetuados por operadores diferentes, o operador mais
preciso será aquele que apresentar menor desvio absoluto médio (dm).
Exemplo 1
Para determinar o ponto de fusão de uma substância, que mais tarde se concluiu ser ácido benzoico (p.f. = 121,7 °C), realizaram-se vários
ensaios, tendo-se obtido os seguintes valores:
1º ensaio : 122,0 °C
2º ensaio: 122,5 °C
3º ensaio: 119,0 °C
4º ensaio: 120,5 °C O termómetro tinha um alcance de 400 °C e uma precisão de 0,5 °C.
COMO AVALIAR A EXATIDÃO
ix
(°C)
Valor
exato
xe
(°C)
Erro
absoluto
Ea = |xi-xe|
(°C)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
*
122,0
121,7
0,3 0,002 0,2
1,0
122,5 0,8 0,007 0,7
119,0 2,7 0,022 2,2
120,5 1,2 0,0099 0,99
1.1. Indique qual das medidas é mais exata.
(R: 122,0 °C, pois é a mais próxima do valor verdadeiro visto ter a menor % Er)
* Nesta situação não era
necessário calcular % média de
erro relativo, uma vez que não
havia outro conjunto de dados
para comparar a exatidão e a
precisão.

2. _____________________________________________________________________________________
Ficha de Trabalho 2
COMO AVALIAR A PRECISÃO
ix
(°C)
x
(°C)
Desvio
absoluto
di =  xi - x 
(°C)
dm
(°C)
122,0
121,0
1,0
1,2
122,5 1,5
119,0 2,0
120,5 0,5
1.2. Qual o valor mais provável para a medição efetuada?
(R: 121,0 °C pois é o valor de x )
1.3. Indique qual das medidas é mais precisa.
(R: 120,5 °C, pois é a mais próxima da média, visto ter o menor desvio absoluto, di)
Incerteza Absoluta de Leitura (IAL)
- se o aparelho for analógico (com escala), a IAL será metade do valor da menor divisão da escala;
- se a aparelho for digital (exibe dígitos), a IAL será o menor valor que pode ser lido no aparelho;
- se o aparelho tiver a indicação explícita, a IAL terá este valor, passando a chamar-se precisão, tolerância ou erro;
Quando se tem uma medição e a IAL (incerteza absoluta de leitura) é com estes elementos que o resultado deve ser apresentado
(ex: V = (3,45  0,05) mL);
Incerteza Absoluta de Observação (IAO)
Quando se tem várias medições e os valores dos desvios absolutos, escolhe-se o maior destes últimos (que será a IAO – incerteza
absoluta de observação).
Incerteza Relativa e incerteza percentual relativa (ou desvio percentual)
Incerteza relativa =
IA
x̅ (média)
Incerteza relativa (%) =
IA
x̅ (média)
× 100
Que valor de incerteza absoluta (IA), selecionar na apresentação do resultado de uma medição?
Quando se tem várias medições, a IAL - incerteza absoluta de leitura e a IAO - incerteza absoluta de observação, compara-se a IAL com a
IAO e o resultado deve ser apresentado com a média das medições e a maior das incertezas, que será designada apenas de IA – Incerteza
Absoluta isto é, se
Se IAL > IAO →símbolo da grandeza = (média  IAL) unidade
Se IAL < IAO → símbolo da grandeza = (média  IAO) unidade
Como apresentar os resultados das medições?
a) Se for pedido para apresentar o resultado em função do valor mais provável e da incerteza absoluta:
Símbolo da grandeza = (média  IA) unidade
b) Se for pedido para apresentar o resultado da medição em função do valor mais provável e da incerteza relativa ou da incerteza
relativa em percentagem (ou desvio percentual):
Símbolo da grandeza = média unidade  IR ou
Símbolo da grandeza = média unidade  IR %

3. _____________________________________________________________________________________
Ficha de Trabalho 3
Relativamente ao exemplo 1:
1.4. Qual é maior? A Incert. Abs. de Leitura ou a Incert. Abs. de Observação?
(R: a IAO, que vale 2,0 °C, visto IAL = 0,5 ºC)
1.5. Indique corretamente o resultado da medição, atendendo ao valor mais provável e à incerteza absoluta.
(R: p.f. = (121,0  2,0) °C (média  maior das incertezas, que neste caso é IAO)
(para este termómetro é indicada a precisão, tolerância ou erro, que vale 0,5 °C, correspondendo à IAL)
Exemplo 2
Para determinar a massa de uma peça, cujo valor real era 1,25 g, efetuaram-se várias pesagens, tendo-se obtido os seguintes valores:
1º ensaio : 1,23 g
2º ensaio: 1,25 g
3º ensaio: 1,27 g
4º ensaio: 1,21 g
5 º ensaio: 1,24 g A balança utilizada nesta experiência tinha uma precisão de 0,01 g
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
1,23
1,25
0,02 0,02 2
2
1,25 0,00 0,00 2
1,27 0,02 0,02 2
1,21 0,04 0,03 3
1,24 0,01 0,008 0,8
ix
(g)
x
(g)
Desvio
absoluto
di =  xi - x 
(g)
dm Incerteza
Absoluta de
Observação
(IAO)
di máx
(ºC) (g)
1,23
1,24
0,01
0,02 0,03
1,25 0,01
1,27 0,03
1,21 0,03
1,24 0,00
2.1. Comente a precisão e a exatidão das medidas efetuadas.
R: o ensaio mais preciso foi o último, pois está mais
próximo da média, visto ter o menor di. O ensaio mais
exato foi o segundo, visto ter a menor % de erro relativo.
2.2.Indique corretamente a medida da massa da peça,
atendendo ao valor mais provável e à incerteza absoluta.
R: sendo a IAO =0,03 g, > IAL = 0,01 g, deverá optar-se
pela IAO, logo o valor da medição efetuada para a massa
da peça será m = (1,24  0,03) g.
2.3.Indique corretamente a medida da massa da peça,
atendendo ao valor mais provável e à incerteza relativa,
expressa em percentagem.
R: incerteza relativa (%) = (0,03 : 1,24) x 100 = 2 %
m = 1,24 g  2 %

4. _____________________________________________________________________________________
Ficha de Trabalho 4
Exercícios
1. Dois estudantes A e B, pretendiam determinar a massa de um corpo, cujo valor era 3,500 g, tendo obtido os seguintes resultados:
ESTUDANTE A
Valor médio das medições ( x ) 3,492 g
Desvio médio das medições (dm) 0,001 g
% média de erro relativo (% Er) 0,240 g
ESTUDANTE B
1ª medição 3,495 g
2ª medição 3,503 g
3ª medição 3,501 g
1.1. Com base nos dados, indique qual o estudante mais preciso e qual o estudante mais exato, justificando a resposta com os
cálculos necessários (é necessário calcular dm e % Er para os dois estudantes).
1.2. Indique o nº de algarismos significativos do desvio médio fornecido na tabela para o estudante A.
1.3. Indique a ordem de grandeza do mesmo desvio médio.
1.4. Indique a massa medida pelo estudante B, atendendo ao valor mais provável e à incerteza absoluta.
1.5. Indique a massa medida pelo estudante B, atendendo ao valor mais provável e à incerteza relativa, expressa em percentagem.
RESOLUÇÃO
Estudante B
ix
(g)
x
(g)
Desvio
absoluto
di =  xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
3,495
3,503
3,501
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
3,495
3,503
3,501
Precisão
Exatidão

5. _____________________________________________________________________________________
Ficha de Trabalho 5
2. Dois analistas, usando os mesmos equipamentos, efetuaram quatro análises independentes à mesma amostra de um medicamento
que continha ácido acetilsalicílico (AAS) e obtiveram os seguintes resultados para a massa de AAS.
ANALISTA 1 0,3110 0,3113 0,3101 0,3108
ANALISTA 2 0,3151 0,3150 0,3152 0,3153
Sabe-se que o valor verdadeiro da quantidade de AAS no comprimido era 0,3112 g.
2.1. Indique qual o analista mais preciso e qual o mais exato (é necessário calcular dm e % Er para os dois analistas).
2.2. Indique a massa medida pelos dois analistas, atendendo ao valor mais provável e à incerteza absoluta.
2.3. Indique a massa medida pelos dois analistas, atendendo ao valor mais provável e à incerteza relativa, expressa em percentagem.
RESOLUÇÃO
Analista 1
ix
(g)
x
(g)
Desvio
absoluto
di = xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
0,3110
0,3113
0,3101
0,3108
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
0,3110
0,3113
0,3101
0,3108
Analista 2
ix
(g)
x
(g)
Desvio
absoluto
di =  Xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
0,3151
0,3150
0,3152
0,3153
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
0,3151
0,3150
0,3152
0,3153
Precisão
Precisão
Exatidão
Exatidão

6. _____________________________________________________________________________________
Ficha de Trabalho 6
FICHA - AVALIAÇÃO DA PRECISÃO E DA EXACTIDÃO DE UM CONJUNTO DE MEDIDAS- correção
Exercício 1 – Resolução
Estudante A
Estudante B
ix
(g)
x
(g)
Desvio
absoluto
di =  xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
3,495
3,500
0,005
0,003 0,0053,503 0,003
3,501 0,001
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
3,495
3,500
0,005 0,001 0,1
0,073,503 0,003 0,0009 0,09
3,501 0,001 0,0003 0,03
1.1. O estudante A foi mais preciso (menor desvio médio) e o estudante B foi mais exato (menor percentagem média de erro relativo).
1.2. dm = 0,001 tem 1 algarismo significativo.
1.3. 0,001 = 1 x 10-3  OG = 10-3 g
1.4. m = (3,500  0,005) g
1.5. m = 3,500 g  0,1 %
Valor médio das medições ( x ) 3,492 g
Desvio médio das medições (dm) 0,001 g
% Média de erro relativo (% Er) 0,240 g
Precisão
Exatidão

7. _____________________________________________________________________________________
Ficha de Trabalho 7
Exercício 2 – Resolução
Analista 1
ix
(g)
x
(g)
Desvio
absoluto
di = xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
0,3110
0,3108
0,0002
0,0004 0,0007
0,3113 0,0005
0,3101 0,0007
0,3108 0,0000
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
0,3110
0,3112
0,0002 0,0006 0,06
0,1
0,3113 0,0001 0,0003 0,03
0,3101 0,0011 0,0035 0,35
0,3108 0,0004 0,001 0,1
Analista 2
ix
(g)
x
(g)
Desvio
absoluto
di =  Xi - x 
(g)
dm
(g)
Incerteza
Absoluta de
Observação
(IAO)
di máx
(g)
0,3151
0,3152
0,0001
0,0001 0,0002
0,3150 0,0002
0,3152 0,0000
0,3153 0,0001
ix
(g)
Valor
exato
xe
(g)
Erro
absoluto
Ea = |xi-xe|
(g)
Erro relativo
Er =
𝐸𝑎
𝑋𝑒
% Er
Er x 100
(%)
% Er
Médio
(%)
0,3151
0,3112
0,0039 0,013 1,3
1,3
0,3150 0,0038 0,012 1,2
0,3152 0,0040 0,013 1,3
0,3153 0,0041 0,013 1,33
2.1. Analisando os resultados, conclui-se que o analista 1 foi mais exato (menor percentagem de erro médio relativo) e o analista 2 foi mais
preciso (menor desvio absoluto médio).
2.2. Analista 1: m = (0,3108  0,0007) g Analista 2: m = (0,3152  0,0002) g
2.3. Analista 1: m = 0,3108 g  0,2 % Analista 2: m = 0,3152  0,06 %
Precisão
Precisão
Exatidão
Exatidão