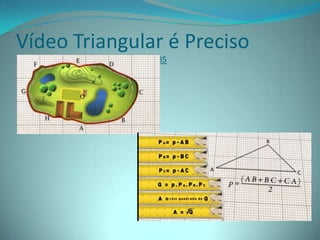
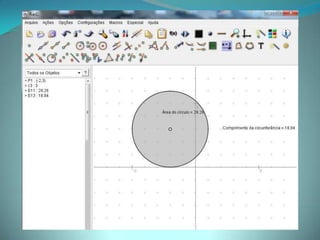
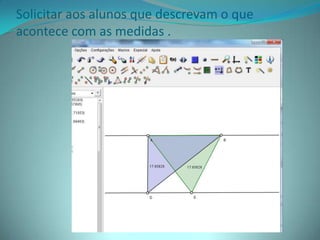
Este documento apresenta um projeto sobre áreas e perímetros de figuras planas utilizando vídeos, software educativo e atividades práticas com alunos do 9o ano do ensino fundamental. O projeto visa explorar o tema de forma contextualizada e estimular os alunos a perceber sua importância no cotidiano através de construções geométricas e cálculos envolvendo circunferências, triângulos, quadriláteros e trapézios.

1. Maria Beatriz de Mattos Richa Ribeiro
9º ano do Ensino Fundamental

2. JUSTIFICATIVA
 Este projeto visa explorar o tema de áreas e perímetros de figuras
planas , mostrando suas aplicações , visualizando em objetos do
nossos cotidiano .
 O trabalho será desenvolvido utilizando a apresentação do tema
através de vídeo projetado no Datashow , com apoio do software
educativo Régua e Compasso para as construções e
demonstrações de figuras e problemas envolvendo situações de
nosso dia-a-dia em que será usado o cálculo de áreas e perímetros
.
 A matemática será mostrada dentro de um contexto cotidiano .
 Os alunos participantes do projeto serão estimulados por
perceber que o tema abordado faz parte de seu cotidiano e
propõe situações em que estão inseridos , percebendo a
importância desta aprendizagem para seu desenvolvimento
social .

3. Vídeo Triangular é Preciso
http://m3.ime.unicamp.br/recursos/1185


4. Conhecendo o Software Régua
e Compasso

5. ATIVIDADES
 1-Círculos e Triângulos
 Construa um círculo de centro (-2, -3) e raio 3. Calcule
a área deste círculo e o comprimento da círculo.
 Construa duas retas paralelas r e s. Um segmento AB
qualquer sobre uma delas. Construa os pontos D e E
sobre a outra. Construa os triângulos ABD e ABE,
calcule suas áreas, movimente D e E e descreva o que
acontece com as medidas das áreas.

7. Solicitar aos alunos que descrevam o que
acontece com as medidas .

8. Quadriláteros Atividade 2 :
Construa um quadrado de lado 4 cm. Determine a círculo inscrita e a circunscrita a
este quadrado, altere a medida do lado do quadrado. Determine a medida de seus
ângulos internos.

9. Os alunos seguirão os
procedimentos para a execução
das atividades sendo o
professor o orientador .

10. Atividade 3 : Construção de quadriláteros
a partir de elementos dados.
• Construir um quadrado dados:
o lado. a=3 cm.
a diagonal. BD=4 cm.
o raio da círculo circunscrita. R=2,5 cm.
o raio da círculo inscrita. r=2 cm.
• Construir um retângulo dados:
os lados. a=4 cm, b=2,5 cm.
diagonal e o lado. a=2,5, d=3,5.
diagonal e o ângulo formado pelas
mesmas. d=4 cm, a=120°.

11. * Construir um losango dados:
as diagonais. AC=5 cm, BD=3 cm.
um lado e uma diagonal. AB=3 cm, AC=4,5.
um lado e um ângulo. AB=3 cm, Cˆ =45°.
*Construir um paralelogramo ABCD dados:
os lados e um ângulo. AB=4 cm, BC=7 cm, Bˆ =45°.
os lados e uma diagonal. AB=5 cm, BC=3 cm, AC=4 cm.
as diagonais e um lado. AC=5 cm, BD=4 cm, BC=2,5 cm.
as diagonais e o ângulo por elas formado. BD=4 cm,
AC=3 cm, a=120°.
os lados e a altura. BC=5 cm, AB=3 cm, hBC=2,5.

12. •
Construir um trapézio ABCD dados:
os lados. AB=5,5 cm, BC=3,5 cm, CD=4 cm, AD=3 cm.
as bases e as diagonais. AB=4,5 cm, CD=3,5 cm,
BD=5,5 cm, AC=5 cm
as bases, uma diagonal e o ângulo formado pelas
diagonais. AB=4,5 cm, AC=4 cm, DC=2,5, AÊB=120° (E
é o ponto de interseção das diagonais).
uma base, dois lados e o ângulo formado por um dos
lados com a base dada. AB=4,5 cm, AD=3 cm, BC=2,5,
Â=60°.

13. “A mente que se abre a uma
nova ideia jamais voltará ao seu
tamanho original”.
(Albert Einstein)