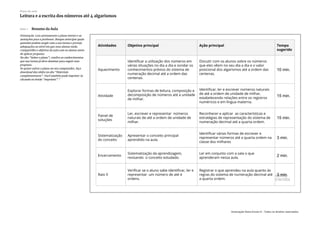
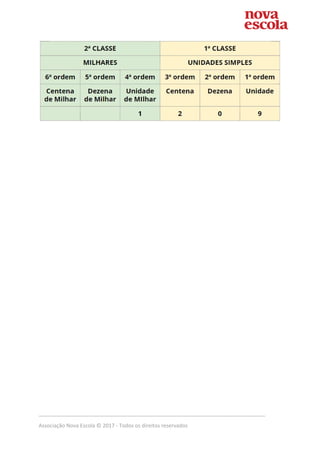
Este plano de aula tem como objetivo desenvolver a leitura e escrita de números até quatro algarismos. A atividade principal introduz a classe dos milhares no sistema de numeração decimal, enquanto os alunos formam números com quatro algarismos. Durante a discussão, o professor guia os alunos a reconhecer as características deste sistema, incluindo o valor posicional e a importância do quadro valor-lugar. Materiais concretos como ábaco e fichas ajudam na compreensão.