O documento apresenta as Leis de Newton da mecânica clássica. A primeira lei estabelece que um corpo permanece em repouso ou movimento uniforme a menos que uma força atue sobre ele. A segunda lei relaciona a força aplicada a um corpo com a variação do seu momento linear. A terceira lei estabelece que as forças exercidas entre dois corpos são iguais em magnitude e opostas em direção. O texto discute os significados dessas leis e como elas permitem definir conceitos fundamentais como massa e for

1. C A P ´I T U L O
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
2
ˆ
MECANICA NEWTONIANA –
PART´ ´
ICULA UNICA
2.1 ¸˜
INTRODUCAO
A ciˆncia da mecˆnica busca fornecer uma descri¸˜o precisa e consistente da dinˆmica de part´
e a ca a ıculas
e sistemas de part´ ıculas, isto ´, um grupo de leis f´
e ısicas descrevem matematicamente os movimentos
dos corpos e agregados de corpos. Para isto, necessitamos de alguns conceitos fundamentais como
distˆncia e tempo que permitem definir a velocidade e acelera¸˜o da part´
a ca ıcula. O terceiro
conceito fundamental, massa, exige alguma elabora¸˜o, que forneceremos quando discutirmos as
ca
Leis de Newton.
As Leis F´ ısicas devem ser baseadas num fato experimental. N˜o podemos esperar a priori
a
que a atra¸˜o gravitacional entre dois corpos deve variar exatamente com o inverso do quadrado
ca
da distˆncia entre eles. Mas experimentos indicam que isso ´ assim. Uma vez que os dados de um
a e
grupo de experimentos tenham sido correlacionados e um postulado tenha sido formulado relativo
ao fenˆmeno a que se referem os dados, ent˜o v´rias implica¸˜es podem ser obtidas. Se essas
o a a co
implica¸˜es forem todas verificadas experimentalmente, podemos acreditar que o postulado ´ ge-
co e
ralmente verdadeiro. O postulado ent˜o assume o status de uma lei f´
a ısica. Se alguns experimentos
discordam com as previs˜es da lei, a teoria deve ser modificada para ser consistente com os fatos.
o
Newton nos forneceu as leis fundamentais da mecˆnica. Declaramos aqui estas leis em termos
a
modernos, discutindo seus significados, ent˜o derivando as implica¸˜es das leis em v´rias situa¸˜es.∗
a co a co
Mas a estrutura l´gica da ciˆncia da mecˆnica n˜o ´ t˜o clara. Nossa linha de racioc´
o e a a e a ınio na
interpreta¸˜o das leis de Newton n˜o ´ a unica poss´ † N˜o discutiremos os detalhes filos´ficos da
ca a e ´ ıvel. a o
mecˆnica mas somente forneceremos a elabora¸˜o das leis de Newton que nos permitem continuar
a ca
com a discuss˜o da dinˆmica cl´ssica. Dedicaremos nossa aten¸˜o neste cap´
a a a ca ıtulo para o movimento
de uma unica part´
´ ıcula, deixando sistemas de part´ ıculas para serem discutidos nos Cap´ ıtulos 9 e
11–13.
∗ Truesdell (Tr68) mostra que Leonhard Euler (1707-1783) esclareceu e desenvolveu os conceitos Newtonianos.
Euler “colocou muito da mecˆnica na sua forma moderna” e “tornou a mecˆnica simples e f´cil” (p. 106).
a a a
† Ernest Mach (1838-1916) expressou seu ponto de vista em seu famoso livro publicado em 1883; E. Mach, Die
Mechanica in Ihrer Entwicklung historisch-Kritisch dargestellt[A ciˆncia da mecˆnica](Praga, 1883). Uma tradu¸˜o
e a ca
da ultima edi¸˜o ´ dispon´
´ ca e ıvel (Ma60). Discuss˜es interessantes tamb´m s˜o proporcionadas por R. B. Lindsay e H.
o e a
Margeneau (Li36) e N. Feather (Fe59).
47

2. 48 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
2.2 LEIS DE NEWTON
Come¸amos simplesmente enunciando na forma convencional as Leis de Newton da mecˆnica∗ :
c a
I. Um corpo permanece em repouso ou em movimento uniforme a menos que atue sobre ele
uma for¸a.
c
II. Um corpo move-se sobre a¸˜o de uma for¸a de tal maneira que a taxa de varia¸˜o temporal
ca c ca
do momento ´ igual a for¸a.
e c
III. Se dois corpos exercem for¸as um sobre o outro, essas for¸as s˜o iguais em magnitude e de
c c a
dire¸˜es opostas.
co
Essas leis s˜o deste modo familiares que algumas vezes tendemos a n˜o perceber os verdadeiros
a a
significados (ou falta deles) como lei f´ ısica. A Primeira Lei, por exemplo, ´ sem sentido sem
e
o conceito de “for¸a”, uma palavra usada por Newton em todas as trˆs leis. De fato, sozinha, a
c e
Primeira Lei conduz a um significado preciso somente se a for¸a for nula; isto ´, o corpo permanece
c e
em repouso ou em movimento uniforme (isto ´, n˜o acelerado e retil´
e a ınio) sem estar sujeito a qualquer
for¸a que seja. O corpo movendo-se dessa maneira ´ denominado como corpo livre (ou part´
c e ıcula
livre). A quest˜o sobre o sistema de referˆncia com respeito ao qual o “movimento uniforme” ´
a e e
medido ser´ discutido na se¸˜o seguinte.
a ca
Destacando a falta deste conte´do na Primeira Lei de Newton, Senhor Arthur Eddington†
u
observou, de certa forma alegremente, o que realmente a lei diz ´ que “todas part´
e ıculas continua em
seu estado de repouso ou em movimento uniforme retil´ ıneo exceto quando for¸ado externamente”.
c
Isto ´ fortemente poss´ para Newton, quem pensou alguma coisa muito clara para seu enunciado.
e ıvel
Mas isso enfatiza que a Primeira Lei a qual por si s´ provanos com a unica no¸˜o qualitativa sobre
o ´ ca
“for¸a”.
c
A segunda Lei fornece um enunciado expl´ ıcito: a For¸a est´ relacionada com a taxa de varia¸˜o
c a ca
temporal do momento. Newton apropriadamente definiu momento (entretanto ele usou o termo
quantidade de movimento) como o produto da massa pela velocidade, tal que
p ≡ mv (2.1)
Portanto, a Segunda Lei de Newton pode ser expressada como
dp d
F= = (mv) (2.2)
dt dt
A defini¸˜o de for¸a torna-se completa e precisa somente quando “massa” ´ definida. Assim a
ca c e
Primeira e a Segunda Leis n˜o s˜o realmente “leis” no senso usual; mais precisamente, elas podem
a a
ser consideradas defini¸˜es. Como o comprimento, tempo e a massa s˜o conceitos j´ entendidos,
co a a
n´s usamos a Primeira e a Segunda Leis de Newton como a defini¸˜o operacional de for¸a. A
o ca c
terceira Lei de Newton, entretanto, ´ realmente uma lei. Ela ´ um enunciado a respeito do mundo
e e
real f´ ısica nas leis de movimento de Newton.‡
ısico (natural) e cont´m toda a f´
e
Devemos adicionar, entretanto, que a Terceira Lei n˜o ´ uma lei geral da natureza. A lei
a e
´ aplicada quando exerce-se uma for¸a em um objeto (pontual) sobre outro objeto (pontual) ´
e c e
∗ Enunciada em 1687 por Sr. Isaac Newton (1642-1727) em Philosophiae naturalis principia mathama-
tica[Principios matem´tica de filosofia natural, normalmente chamada de Principia](Londres, 1687). Anteriormente,
a
Galileo (1564-1642) generalizou os resultados dos seus pr´prios experimentos matem´ticos com suposi¸˜es equiva-
o a co
lentes a Primeira e Segunda Leis de Newton. Mas Galileu n˜o forneceu uma descri¸˜o completa da dinˆmica porque
a ca a
ele n˜o conhecia o significado da terceira Lei de Newton - e portanto faltou determinar preciamente o significado de
a
for¸a
c
† Senhor Arthur Eddington (Ed30, p. 124).
‡ O presente racioc´
ınio aqui, a saber, a Primeira e Segunda Leis s˜o realmente defini¸˜es e a Terceira Lei cont´m
a co e
a F´ısica, esta n˜o ´ a unica interpreta¸˜o poss´
a e ´ ca ıvel. Lindsay and Margenau (Li36), por exemplo, apresentam que as
duas primeira Leis s˜o Leis F´
a ˜
ısicas e entAo derivam a Terceira Lei como uma conseq¨ˆncia.
ue
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

3. 2.2. LEIS DE NEWTON --- 49
direcionada ao longo de uma linha que une os objetos. Tais for¸as s˜o chamadas for¸as centrais;
c a c
a Terceira Lei ´ aplicada se a for¸a central ´ atrativa ou repulsiva. As for¸as gravitacional e ele-
e c e c
trost´tica s˜o for¸as centrais, assim as Leis de Newton podem ser usadas em problemas envolvendo
a a c
esses tipos de for¸as. As vezes for¸as el´sticas (as quais s˜o realmente manifesta¸˜es macrosc´picas
c c a a co o
de for¸as eletrost´ticas microsc´picas) s˜o centrais. Por exemplo, dois objetos pontuais conectados
c a o a
diretamente por uma mola ou corda el´tica s˜o sujeitos a for¸as que obedecem a Terceira Lei.
a a c
Alguma for¸a que depende da velocidade de intera¸˜o entre os corpos ´ n˜o central, e a Terceira
c ca e a
Lei n˜o pode ser aplicada. For¸as dependentes da velocidade s˜o cracter´
a c a ısticas de intera¸˜es que
co
se propagam com velocidades finitas. Assim a for¸a entre cargas em movimento n˜o obedece a
c a
Terceira Lei, porque a for¸a se propaga com a velocidade da luz. At´ mesmo a for¸a gravitacio-
c e c
nal entre corpos em movimento ´ dependente da velocidade, mas o efeito ´ pequeno e de dif´
e e ıcil
detec¸˜o. O unico efeito observado ´ a precess˜o do peri´lio dos planetas mais internos (visto na
ca ´ e a e
se¸˜o 8.9). Retornaremos a discuss˜o da Terceira Lei de Newton no Cap´
ca a ıtulo 9.
Para demonstrar o significado da Terceira Lei de Newton, vamos parafrase´-lo da seguinte
a
maneira, o qual incorpora a defini¸˜o apropriada de massa:
ca
III’. Se dois corpos constituiem um sistema ideal e isolado, ent˜o as acelera¸˜es destes corpos s˜o
a co a
sempre em dire¸˜es opostas, e a raz˜o da magnitude das acelera¸˜es ´ constante. Esta raz˜o
co a co e a
constante ´ o inverso da raz˜o das massas dos corpos.
e a
Com esse procedimento, podemos dar a defini¸˜o pr´tica de massa e dessa forma fornecer um signi-
ca a
ficado preciso para as equa¸˜es que resumem a dinˆmica Newtoniana. Para dois corpos isolados,
co a
1 e 2, a Terceira Lei diz que
F1 = −F2 (2.3)
Usando a defini¸˜o de for¸a como apresentado pela Segunda Lei, temos
ca c
dp1 dp2
=− (2.4a)
dt dt
ou, com massas constantes,
dv1 dv2
m1 = m2 − (2.4b)
dt dt
e, como a acelera¸˜o ´ derivada temporal da velocidade,
ca e
m1 (a1 ) = m2 (− a2 ) (2.4c)
Portanto,
m2 a1
=− (2.5)
m1 a2
onde o sinal negativo indica somente que os vetores acelera¸˜o est˜o em dire¸˜es opostas. A massa
ca a co
´ considerada uma grandeza positiva.
e
Sempre podemos selecionar, digamos, m1 como unidade de massa. Ent˜o, comparando a
a
rela¸˜o das acelera¸˜es onde m1 ´ permitido interagir com qualquer outro corpo, podemos deter-
ca co e
minar a massa do outro corpo. Para medir as acelera¸˜es, devemos ter rel´gios e r´guas apropria-
co o e
das; tamb´m, devemos escolher um sistema de coordenadas ou sistema de referˆncia adequado. A
e e
quest˜o de um “sistema de referˆncias adequado” ´ discutido na pr´xima se¸˜o.
a e e o ca
Um dos mais comuns m´todos de determina¸˜o de massa de um objeto ´ pela pesagem – por
e ca e
exemplo pela compara¸˜o de seu peso a de um padr˜o por meio de uma balan¸a de contra peso.
ca a c
Esse procedimento faz uso do fato que em um campo gravitacional o peso de um corpo ´ apenas
e
a for¸a gravitacional agindo no corpo; isto ´, a equa¸˜o de Newton F = ma se torna W = mg,
c e ca
onde g ´ acelera¸˜o devido a gravidade. A validade do uso desse procedimento apoia-se em uma
e ca
hip´tese fundamental: que a massa m que aparece na equa¸˜o de Newton ´ definida de acordo
o ca e
com enunciado III ´ igual a massa m que aparece na equa¸˜o da for¸a gravitacional. Essas duas
e ca c
massas s˜o chamadas de massa inercial e massa gravitacional, respectivamente. As defini¸˜es
a co
podem ser enunciadas como segue:
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

4. 50 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Massa Inercial: ´ a massa que determina a acelera¸˜o de um corpo sob a a¸˜o de uma dada
e ca ca
for¸a.
c
Massa Gravitacional: ´ a massa que determina as for¸as gravitacionais entre um corpo e
e c
outros corpos.
Galileu foi o primeiro a testar a equivalˆncia de massa inercial e massa gravitacional em
e
seu (possivelmente falso) experimento com quedas de objetos na Torre de Pisa. Newton tamb´m e
considereou o problema e mediu os per´ ıodos de pˆndulos de comprimento iguais mas com materiais
e
diferentes. Nem Newton nem Galileu encontraram qualquer diferen¸a mas os m´todos foram tanto
c e
rudimentares.∗ Em 1890 E¨tv¨s† inventou um m´todo engenhoso para testar a equivalˆncia das
o o e e
massas inerciais e gravitacionais. Usando dois ojetos feitos com materiais diferentes, ele comparou
o efeito da for¸a gravitacional da Terra (isto ´, o peso) com o efeito da for¸a inercial causada
c e c
pela rota¸˜o da terra. O experimento envolveu um m´todo de efeito nulo usando uma balan¸a de
ca e c
tor¸˜o sens´ e por essa raz˜o foi altamente preciso. Experiemntos mais recentes (notavelmente
ca ıvel a
os de Dicke ‡ ), usando essencialmente o mesmo m´todo teve melhor precis˜o, e sabemos agora que
e a
a massa inercial e a massa gravitacional s˜o idˆnticas dentro de algumas partes em 101 2. Esse
a e
resultado ´ consideravelmente importante na teoria geral da relatividade § . A afirma¸˜o da exata
e ca
igualadade da massa gravitacional ´ expressa com principio de equivalˆncia.
e e
A terceira lei de Newton ´ declarada em termos de dois corpos que consistem um sistema
e
´
isolado. E imposs´ ıvel alcan¸ar tal condi¸˜o ideal; cada corpo no universo interage com todos os
c ca
outros corpos, embora a for¸a de intera¸˜o possa ser muito fraca para ser de qualquer importˆncia
c ca a
pr´tica se grandes distˆncias s˜o envolvidas. Newton evitou a quest˜o de como distinguir o efeito
a a a a
desejado de todos os outros efeitos estranhos. Mas esta pr´tica dificilmente enfatizar´ sozinha a
a a
ca ´
enormidade da afirma¸˜o de Newton na Terceira Lei. E um tributo ` profundidade da percep¸˜o
a ca
dele e a perspic´cia f´
a ısica das conclus˜es baseando-se em observa¸˜es limitadas, prosperamente
o co
sustentou o teste de experimento por 300 anos. Apenas neste s´culo houve medidas com detal-
e
hes suficientemente relevantes contendo discrepˆncias com as predi¸˜es da teoria de Newton. A
a co
persegui¸˜o desses detalhes conduziu ao desenvolviemnto da teoria da relatividade e da mecˆnica
ca a
quˆntica¶ . Outra interpreta¸˜o da Terceira Lei de Newton ´ baseada no conceito de momento
a ca e
arranjando a Equa¸˜o 2.4a fornece
ca
d
(p1 + p2 ) = 0
dt
ou
p1 + p2 = constante (2.6)
A declara¸˜o que momento ´ conservado na intera¸˜o isolada de duas part´
ca e ca ıculas ´ um caso especial
e
de uma declara¸˜o mais geral conserva¸˜o de momento linear. F´
ca ca ısicos apreciam leis de con-
serva¸˜o gerais, e a conserva¸˜o de momento linear acredita-se ser sempre obedecida, mais tarde
ca ca
modificaremos nossas defini¸˜es de momento da Equa¸˜o ?? para altas velocidades aproximando-se
co ca
a velocidade da luz.
2.3 ˆ
SISTEMAS DE REFERENCIAS
Newton percebeu que, para as leis de movimento terem significado, o movimento dos corpos devem
ser medidos relativos ao mesmo sistema de refˆncia. O sistema de refˆncia ´ chamado de referˆncia
e e e e
inercial se as leis de Newton s˜o validas realmente neste sistema; que ´, se um corpo n˜o est´
a e a a
∗ Noexperimento de Newton, ele pode ter detectado uma diferen¸a de somente uma parte em 103 .
c
† Roland Van E¨tv¨s (1848- 1919) um conde H´ ngaro, sua pesquisa em problemas gravitacionais conduziram ao
o o u
desenvolvimento de um gravitˆmetro, o qual foi usado em estudos geol´gicos.
o o
‡ P. G. Roll, R. Krotkov e R. H. Dicke, Ann. Phys. (n.Y.) 26, 442 (1964) Ver tamb´m BraginsKy e Pavov, Sov.
e
Phys. - JETP 34, 463 (1972).
§ Ver, por exemplo, as discurss˜es feitas por P. G. Bergmann (Be96) eJ. Weber (We61). Olivro de Weber tamb´m
o e
fornece uma an´lise do experimento de E¨tv¨s.
a o o
¶ Ver tamb´m a Se¸˜o 2.8.
e ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

5. ˆ
2.3. SISTEMAS DE REFERENCIAS --- 51
sujeito a for¸as externas move-se em uma linha reta com velocidade constante (ou se mant´m
c e
em repouso), ent˜o o sistema de coordenadas que estabelece este fato ´ um sistema de referˆncia
a e e
inercial. Esta ´ uma defini¸˜o operacional clara e um que tamb´m segue da teoria da relatividade
e ca e
geral.
Se as leis de Newton s˜o v´lidas em um sistema de referˆncia, ent˜o elas tamb´m s˜o v´lidas
a a e a e a a
em qualquer sistema de referˆncia em movimento uniforme (isto ´, n˜o acelerado) com respeito
e e a
ao primeiro sistema.∗ Este ´ um resultado do fato que a equa¸˜o F =m¨ envolve uma derivada
e ca r
segunda de r: Uma mudan¸a de coordenadas envolvendo uma velocidade constante n˜o influˆncia
c a e
a equa¸˜o. Este resultado ´ chamado de invariˆncia de Galileu ou princ´
ca e a ıpio da relatividade
Newtoniana.
A teoria da relatividade tem mostrado que os conceitos de repouso absolutos e um sistema de
referˆncia descrito inercial absoluto n˜o tem sentido. Ent˜o mesmo que adotemos um sistema de
e a a
referˆncia descrito com respeito `s estrelas “fixas” – e realmente tais sistemas as equa¸˜es Newto-
e a co
nianas s˜o v´lidas com um alto grau de precis˜o – tal sistema n˜o ´ na realidade um referˆncial
a a a a e e
inercial absoluto. Todavia podemos considerar as estrelas “fixas” para definir um sistema de re-
ferˆncia que se aproxima de um referˆncia inercial “absoluta” para que at´ certos pontos satisfa¸am
e e e c
ao nosso prop´sito.
o
Embora o sistema de referˆncia das estrelas-fixas seja um sistema convencionalmente defin´
e ıvel
e conveniente para muitos prop´sitos, devemos enfatizar que as defini¸˜es fundamentais de um
o co
referˆncial inercial n˜o fazem men¸˜es as estrelas fixas ou vice-versa. Se um corpo n˜o est´ sujeito
e a co a a
a for¸as e movimenta-se com velocidade constante em um certo referˆncial, este sistema ´, por
c e e
defini¸˜o um sistema de referˆncia inercial. Como a descri¸˜o precisa de movimento de um objeto
ca e ca
f´
ısico real no mundo f´ ısico real ´ normalmente dificil, usaremos idealiza¸˜es e aproxima¸˜es de
a co co
graus variados; isto ´: desprezaremos as for¸as mais fracas sobre o corpo se estas for¸as n˜o afetam
e c c a
significativamente o corpo.
Se desejarmos descrever o movimento de, digamos, de uma part´ ıcula livre e se escolhermos
para esse prop´sito algum sistema de coordenadas num referˆncial inercial, ent˜o requeremos que
o e a
a equa¸˜o (vetorial) do movimento da part´
ca ıcula seja independente da posi¸˜o da origem do sis-
ca
tema coordenado e independente de sua orienta¸˜o no espa¸o. Al´m disso iremos requerer que
ca c e
o tempo seja homogˆneo; isto ´, uma part´
e e ıcula livre movendo-se com velocidade constante no
sistema coordenado durante um certo intervalo de tempo que n˜o deve ser durante um intervalo
a
de tempo posterior, seja encotrado movendo-se com velocidade diferente.
Podemos ilustrar a importˆncia dessas propriedades pelo seguinte exemplo. Considere como
a
na Figura 2-1, uma part´ ıcula livre movendo-se ao longo de uma trajet´ria AC. Para descrever o
o
movimento da part´ ıcula, vamos escolher um sistema de coordenadas retangulares no qual a origem
de move em um c´ ırculo, como mostrado. Para simplificar, vamos formar a orienta¸˜o dos eixos fixo
ca
no espa¸o. A part´
c ıcula move-se com uma velocidade relativa vp relativo a um referencial inercial.
Se o sistema de coordenadas move-se com uma velocidade linear vc quando passa no ponto B, e
se vc = vp , ent˜o para um observador no sistema de coordenadas m´vel a part´
a o ıcula (em A) parece
estar em repouso. Algum tempo depois, no entanto, quando a part´ ıcula est´ em C e o sistema
a
de coordenadas em D, a part´ ıcula parecer´ estar acelerada em rela¸˜o ao observador. Devemos,
a ca
portanto, concluir que o sitema de coordenadas em rota¸˜o n˜o pode ser considerado um referencial
ca a
inercial.
Estas observa¸˜es n˜o s˜o suficientes para decidir se o tempo ´ homogˆneo. Para alcan¸ar
co a a e e c
semelhantes conclus˜es, repetidas medidas devem ser feitas em situa¸˜es idˆnticas em diversos
o co e
instantes de tempo; idˆnticos resultados indicar˜o a homogeneidade do tempo.
e a
As equa¸˜es de Newton n˜o descrevem o movimento dos corpos em sistemas de referˆncia n˜o-
co a e a
inercial. Podemos desenvolver um m´todo para descrever o movimento de uma part´
e ıcula para um
sistema de coordenadas em rota¸˜o, mas, como ser´ visto no Cap´
ca a ıtulo 10, as equa¸˜es resultantes
co
∗ No Cap´ıtulo 10, discutiremos as modifica¸˜es que devem ser feitas nas equa¸˜es de Newton se desejamos
co co
descrever o movimento de um corpo em rela¸˜o a um sistema de referˆncia n˜o inercial, isto ´, um referˆncia que
ca e a e e
est´ acelerado em rela¸˜o a um referˆncia inercial.
a ca e
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

6. 52 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
FIGURA 2-1
contˆm v´rios termos que n˜o aparecem na simples equa¸˜o Newtoniana F = ma. Para o momento,
e a a ca
ent˜o, restringimos nossa aten¸˜o para os sistemas de referˆncia inercial para descrever a dinˆmica
a ca e a
de part´ıculas.
2.4 A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA
A equa¸˜o newtoniana F = dp/dt podem expressar alternativamente como
ca
d dv
F= (mv) = m = m¨
r (2.7)
dt dt
se adotarmos que a massa m n˜o varia com o tempo. Esta ´ uma equa¸˜o diferencial de segunda
a e ca
ordem que pode ser integrada para encontrar r = r(t) se a fun¸˜o F ´ conhecida.
ca e
Especificando os valores iniciais de r e r = v obtemos as duas constantes arbrit´rias da
˙ a
integra¸˜o. Ent˜o determinamos o movimento da part´
ca a ıcula pela fun¸˜o da for¸a F e os valores
ca c
iniciais para a posi¸˜o r e a velocidade v.
ca
A for¸a F pode ser uma fun¸˜o de alguma combina¸˜o da posi¸˜o, velocidade e tempo, e
c ca ca ca
´ geralmente denotada como F(r, v, t). Para um certo sistema dinˆmico, normalmente queremos
e a
saber r e v como uma fun¸˜o do tempo. Isto ´ obtido resolvendo a Equa¸˜o 2.7 em ¨. A aplica¸˜o
ca e ca r ca
da Equa¸˜o 2.7 para situa¸˜es f´
ca co ısicas ´ uma importante parte da mecˆmica.
e a
Neste cap´ ıtulo, estudaremos v´rios exemplos no qual a fun¸˜o for¸a ´ conhecida. Iniciaremos
a ca c e
usando fun¸˜es for¸a mais simples (constante ou dependente somente de r, ou v ou t) em uma
co c
dimens˜o espacial somente, como uma revis˜o das disciplinas b´sicas de f´
a a a ısica. Isso ´ importante
e
a ca ˜
para formar bons h´bitos na resolu¸˜o de problemas. Abaixo sAo apresentadas algumas t´cnicas e
uteis para resolver problemas.
´
1. Fazer um esbo¸o (esquema gr´fico – desenho) do problema, indicando as for¸as, velocidade
c a c
e assim por diante.
2. Escreva as grandezas e seus valores fornecidos.
3. Escreva as equa¸˜es que ser˜o utilizadas e o que ´ para ser determinanado.
co a e
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

7. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 53
4. As equa¸˜es que descrevem o problema normalmente devem ser manipuladas a fim de achar
co
a grandeza procurada. Manipula¸˜es alg´bricas bem como a diferencia¸˜o ou integra¸˜o s˜o
co e ca ca a
usualmente exigidas. Algumas vezes c´lculos num´ricos usando o computador s˜o mais f´ceis,
a e a a
se for o unico m´todo para a solu¸˜o.
´ e ca
5. Finalmente, coloque os valores reais fornecidos, para obter os valores das vari´veis das gran-
a
dezas procuradas.
Vamos considerar o problema do bloco deslizando no plano inclinado. O ˆngulo do plano inclinado
a
´ θ e a massa do bloco ser´ 100 g. O esquema do problema ´ mostrado na Figura 2-2a.
e a e
E X E M P L O 2.1 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −−
Se um bloco desliza sem atrito sob um plano inclinado fixo, θ = 30o , qual ´ a acelera¸˜o
e ca
deste?
FIGURA 2-2
Solu¸˜o: Duas for¸as atuam no bloco (ver Figura 2-2a): a for¸a gravitacional Fg e a for¸a normal
ca c c c
do plano N empurrando para cima no bloco (sem atrito neste exemplo). O bloco ´ pressionado
e
para ficar sobre o plano, e a unica dire¸˜o que ele pode se mover ´ na dire¸˜o x, subindo e descendo
´ ca e ca
o plano. N´s tomamos a dire¸˜o + x para descer o plano. A for¸a resultante F ´ constante; a
o ca c e
Equa¸˜o 2.7 se torna
ca
F = Fg + N
e porque F ´ a for¸a resultante do sistema que atua no bloco,
e c
F = m¨
r
ou
Fg + N = m¨
r (2.8)
Este vetor deve ser aplicado em duas dire¸˜es: x e y (perpendicular a x). A componente da
co
for¸a na dire¸˜o y ´ zero, porque n˜o ocorre acelera¸˜o nesta dire¸˜o. A for¸a Fg est´ dividida
c ca e a ca ca c a
vetorialmente dentro de suas componentes x e y (linhas na Figura ??a). A Equa¸˜o 2.8 se torna
ca
dire¸˜o y
ca
−Fg cos θ + N = 0 (2.9)
dire¸˜o x
ca
Fg sin θ = m¨
x (2.10)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

8. 54 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
com o resultado adquirido
Fg mg sin θ
x=
¨ sin θ = = g sin θ
m m
g
x = g sin (30◦ ) = = 4.9m/s2
¨ (2.11)
2
Portanto, a acelera¸˜o do bloco ´ constante.
ca e
Podemos encontrar a velocidade do bloco ap´s este se mover do repouso uma distˆncia x0
o a
descendo o plano pela multiplica¸˜o da Equa¸˜o 2.11 por 2x e integrando
ca ca ˙
2x¨ = 2xg sin θ
˙x ˙
d 2 dx
(x ) = 2g sin θ
˙
dt dt
2
v0 x0
d(x2 ) = 2g sin θ
˙ dx
0 0
Para t = 0, ambos x = x = 0, e, para t = tf inal , x = x0 , e a velocidade x = v0 .
˙ ˙
2
v0 = 2g sin θx0
v0 = 2g sin θx0
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.2 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Se o coeficiente de atrito est´tico entre o bloco e o plano previsto do exemplo anterior
a
´ µs = 0.4, em que ˆngulo θ o bloco come¸ar´ a deslizar se estiver inicialmente em
e a c a
repouso?
Solu¸˜o: Necessitamos de uma for¸a de atrito adicional f (veja Figura 2.2b). A for¸a de atrito
ca c c
est´tica tem o valor m´ximo aproximado
a a
fmax = µs N (2.12)
e a Equa¸˜o 2.7 torna-se, na forma de suas componentes,
ca
dire¸˜o y
ca
−Fg cos θ + N = 0 (2.13)
dire¸˜o x
ca
−fs + Fg sin θ = m¨
x (2.14)
A for¸a de atrito est´tica fs ter´ algum valor entre fs ≤ fmax para manter x = 0 – para manter o
c a a ¨
bloco em repouso. Entretanto, o ˆngulo θ do plano aumenta, logo a for¸a de atrito est´tica ser´
a c a a
incapaz de manter o bloco no repouso. Nesse ˆngulo θ , fs torna-se
a
fs (θ = θ ) = fmax = µs N = µs Fg cos θ
e
m¨ = Fg sin θ − fmax
x
m¨ = Fg sin θ − µs Fg cos θ
x
x = g(sin θ − µs cos θ)
¨ (2.15)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

9. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 55
Imediatamente antes do bloco come¸ar deslizar, a acelera¸˜o ´ x = 0, assim
c ca e ¨
sin θ − µs cos θ = 0
tan θ = µs = 0.4
θ = tan−1 (0.4) = 22◦
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.3 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Depois que o bloco do exemplo anterior come¸a a deslizar, o coeficiente da fric¸˜o
c ca
cin´tica (do movimento) torna-se µk = 0.3. Encontre a acelera¸˜o para o ˆngulo de
e ca a
θ = 30o .
Solu¸˜o: Similarmente ao Exemplo 2.2, a fric¸˜o cin´tica torna-se (aproximadamente)
ca ca e
fk = µk N = µk Fg cos θ (2.16)
e
m¨ = Fg sin θ − fk = mg(sin θ − µk cos θ)
x (2.17)
x = g(sin θ − µk cos θ) = 0.24g
¨ (2.18)
Geralmente, a for¸a de fric¸˜o est´tica (fmax = µs N ) ´ maior que aquela da fric¸˜o cin´tica
c ca a e ca e
(fk = µk N ). Isto pode ser observado em uma experiˆncia simples. Se diminuirmos o ˆngulo θ
e a
abaixo de 16.7o , encontramos que x < 0, e o bloco permanece parado. Se levantarmos o apoio do
¨
bloco acima de θ = 16.7o , encontramos que o bloco n˜o inicia o movimento novamente at´ que
a e
θ ≥ 22o . A fric¸˜o est´tica determina quando o movimento tem in´ novamente. N˜o h´ uma
ca a ıcio a a
acelera¸˜o descontinua enquanto o bloco come¸a se mover devido a diferen¸a entre µs e µk . Para
ca c c
velocidades pequenas, o coeficiente de fric¸˜o muda rapidamente de µs a µk .
ca
O assunto da fric¸˜o ´ ainda uma ´rea de pesquisa interessante e importante. H´ sempre
ca e a a
algumas surpresas. Por exemplo, mesmo que calcul´ssemos o valor absoluto da for¸a de fric¸˜o
a c ca
como f = µN , a pesquisa mostrou que a for¸a de fric¸˜o ´ diretamente proporcional, n˜o `
c ca e a a
carga, mas ` ´rea de contato microsc´pica entre os dois objetos (ao contr´rio da ´rea de contato
aa o a a
aparente). N´s usamos o µN como uma aproxima¸˜o porque, enquanto N aumenta, ”faz assim a
o ca
a
´rea de contato real em um n´ microsc´pico”. Por centenas de anos antes dos 1940s, aceitou-se
ıvel o
que a carga – e n˜o a ´rea – eram respons´veis diretamente. Acreditamos tamb´m que a for¸a de
a a a e c
fric¸˜o est´tica ´ maior que aquela de fric¸˜o cin´tica porque a liga¸˜o dos ´tomos entre os dois
ca a e ca e ca a
objetos n˜o tem como se desenvolver por muito tempo no movimento cin´tico.
a e
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
EFEITO DAS FORCAS DE RETARDAMENTO
¸
Devemos enfatizar que a for¸a F na Equa¸˜o 2.7 n˜o ´ necessariamente constante, e de fato, ela
c ca a e
pode consistir de v´rias partes distintas, como vimos nos exemplos anteriores. Por exemplo, se
a
uma part´ıcula cai num campo gravitacional constante, a for¸a gravitacional ´ Fg = mg, onde g ´
c e e
a acelera¸˜o da gravidade. Se conjuntamente, existe uma for¸a de retardamento Fr e que ´ uma
ca c e
fun¸˜o da velocidade instantˆnea, ent˜o a for¸a total ´
ca a a c e
F = Fg + Fr
= mg + Fr (v) (2.19)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

10. 56 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Geralmente ´ suficiente considerar que Fr (v) ´ simplesmente proporcional a alguma potˆncia da
e e e
velocidade. Em geral, as for¸as de retardamento reais s˜o mais complicadas, mas a aproxima¸˜o
c a ca
pela lei das potˆncias ´ util em muitas ocasi˜es na qual a velocidade n˜o tem grandes varia¸˜es.
e e ´ o a co
Neste caso, se Fr ∝ v n , ent˜o a equa¸˜o de movimento pode geralmente ser integrada diretamente
a ca
ao passo que, se a real dependˆncia da velocidade for usada, provavelmente ser´ necess´rio uma
e a a
integra¸˜o num´rica. Com a aproxima¸˜o da lei da potˆncia, podemos escrever
ca e ca e
v
F = mg − mkv n (2.20)
v
onde k ´ uma constante positiva que especifica o poder da for¸a de retardamento e v/v ´ um vetor
e c e
unit´rio na dire¸˜o de v. Experimentalmente, encontramos que, para um objeto relativamente
a ca
pequeno movendo-se no ar, n ∼ 1 para velocidades menores que aproximadamente 24 m/s (∼ 80
=
ft/s). Para altas velocidades mas com valores abaixo da velocidade do som (∼ 330 m/s ou 1.100
ft/s), a for¸a de retardamento ´ aproximadamente proporcional ao quadrado da velocidade.∗ Para
c e
simplificar, a dependˆncia de v 2 quase sempre ´ usada para velocidades acima da velocidade do
e e
som.
O efeito da resistˆncia do ar ´ importante, por exemplo, para um jogo de ping-pong, uma bola
e e
leve movendo-se velozmente desvia sua trajet´ria e, para um proj´til de morteiro lan¸ado contra um
o e c
inimigo. Extensa tabelas foram constru´ ıdas para proj´teis bal´
e ısticos militares de diferentes tipos
com a velocidade em fun¸˜o do tempo de vˆo. Existem v´rias for¸as atuando sobre um proj´til
ca o a c e
em vˆo. A resistˆncia do ar ´ chamada de for¸a de arraste W e ´ oposta a velocidade do proj´til,
o e e c e e
como mostra a Figura 2-3a. A velocidade v n˜o ´ normalmente paralela ao eixo de simetria do
a e
proj´til. O componente da for¸a atuando perpendicularmente a for¸a de arraste ´ conhecida, como
e c c e
for¸a de ascens˜o La . Deve haver tamb´m outras for¸as devido a rota¸˜o e oscila¸˜o do proj´til, e
c a e c ca ca e
um c´lculo da trajet´ria bal´
a o ıstica do projeto ´ extremamente complexo. A express˜o de Prandtl
e a
para resistˆncia do ar†´
e e
1
W = cW ρAv 2 (2.21)
2
onde cW ´ o coeficiente de arraste adimensional, ρ ´ a densidade do ar, v ´ a velocidade e A
e e e
´ a ´rea da sec¸˜o reta do objeto (proj´til) medida perpendicularmente com a velocidade. Nas
e a ca e
Figuras 2-3b, plotamos alguns valores t´ıpicos para cW , e nas Figuras 2-3c e d podemos calcular a
resistˆncia W usada na Equa¸˜o 2.21 para um proj´til de diˆmetro 10 cm e usando os valores de cW
e ca e a
apresentados. A resistˆncia do ar aumenta drasticamente pr´ximo ` velocidade do som (n´mero de
e o a u
Mach M = velocidade/velocidade do som). Abaixo das velocidades de aproximadamente 400 m/s
´ evidente que uma equa¸˜o de pelo menos segundo grau ´ necess´ria para descrever a for¸a de
e ca e a c
resistˆncia. Para altas velocidades, o retardamento da for¸a varia aproximadamente linearmente
e c
com a velocidade.
V´rios exemplos de movimento de uma part´
a ıcula sujeita a v´rias for¸as s˜o descritas a se-
a c a
guir. Esses exemplos s˜o particularmente bons para a inicia¸˜o a c´lculos computacionais usando
a ca a
alguns dos programas comerciais de matem´tica simb´lica, de planilhas ou para os estudantes es-
a o
creverem seus pr´prios programas. Os resultados computacionais, especialmente os gr´ficos podem
o a
muitas vezes ser comparados com os resultados anal´ ıticos apresentamos aqui. Algumas das Figu-
ras mostradas nesta se¸˜o foram produzidas usando c´lculos computacionais, e v´rios problemas
ca a a
propostos no final do cap´ ıtulo s˜o propostos para os estudantes iniciarem experiˆncias no uso do
a e
computador, se assim desejar o professor ou estudante.
∗ O movimento de uma part´ ıcula num meio na qual h´ uma for¸a resistente proporcional a velocidade ou com o
a c
quadrado da velocidade (ou uma combina¸˜o linear das duas) foi estudado por Newton em seu Principia (1687). A
ca
extens˜o para alguma potˆncia da velocidade foi feito por Joham Bernoulli em 1711. O termo lei da resistˆncia de
a e e
Stokes ´ algumas vezes aplicada para uma for¸a resistente proporcional a velocidade; a lei da resistˆncia de Newton
e c e
´ uma for¸a de retardamento proporcional ao quadrado da velocidade.
e c
† Veja o artigo de E. Melchior e H. Reuschel no “Handbook on Weaponry” (Rh82, p.137)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

11. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 57
FIGURA 2-3 (a) For¸as aerodinˆmicas agindo no proj´til. W ´ a for¸a de arraste (for¸a da resistˆncia do ar) e ´ oposta
c a e e c c e e
a velocidade do proj´til v. Observe que v dever´ estar num ˆngulo α com o eixo da simetria do proj´til. O componente
e a a e
da for¸a de a¸˜o perpendicular a for¸a de arraste ´ chamada de for¸a de ascens˜o Fa . O ponto D ´ o centro de press˜o.
c ca c e c a e a
Finalmente, a for¸a gravitacional Fg age para baixo. Se o centro de press˜o n˜o est´ no centro de massa do proj´til, h´
c a a a e a
tamb´m um torque em torno do centro de massa. (b) O coeficiente de arraste cW , da lei de resistˆncia de Rheinmetall
e e
(Rh82), ´ plotado como fun¸˜o do n´ mero M de Mach . Observe a grande varia¸˜o pr´xima da velocidade do som onde
e ca u ca o
M = 1. (c) A for¸a de resistˆncia do ar W (for¸a de arraste) ´ mostrada com uma fun¸˜o da velocidade para um proj´til de
c e c e ca e
diˆmetro igual a 10 cm. Observe a inflex˜o pr´xima da velocidade do som. (d) Mesma an´lise de (c) para altas velocidades.
a a o a
E X E M P L O 2.4 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −−
Como um exemplo simples de movimento resistivo de uma part´
ıcula, encontramos o
movimento e a velocidade do movimento horizontal em um meio em que a for¸a de
c
retardamento ´ proporcional a velocidade
e
Solu¸˜o: Um esbo¸o do problema ´ mostrado na Figura 2-4. A Equa¸˜o Newtoniana F = ma
ca c e ca
fornece-nos equa¸˜o de movimento: dire¸˜o x
ca ca
dv
ma = m = −kmv (2.22)
dt
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

12. 58 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
FIGURA 2-4
onde kmv ´ a magnitude da for¸a de resistˆncia (k = constante). Portanto
e c e
dv
= −k dt
v
ln v = −kt + C1 (2.23)
A integra¸˜o constante na Equa¸˜o 2.23 pode ser avaliada se prescrevermos a condi¸˜o inicial
ca ca ca
v(t = 0) ≡ v0 . Logo C1 = ln v0 , e
v = v0 e−kt (2.24)
Podemos integrar esta equa¸˜o para obter o deslocamento x como fun¸˜o do tempo:
ca ca
dx
v= = v0 e−kt
dt
v0 −kt
x = v0 e−kt dt = − e + C2 (2.25a)
k
A condi¸˜o inicial x(t = 0) ≡ 0 implica C2 = v0 /k. Ent˜o
ca a
v0
x= (1 − e−kt ) (2.25b)
k
Este resultado mostra que x aproxima-se do valor v0 /k conforme t → ∞.
Podemos tamb´m obter a velocidade como fun¸˜o do deslocamento escrevendo
e ca
dv dv dt dv 1
= = .
dx dt dx dt v
portanto
dv dv
v = = −kv
dx dt
ou
dv
= −k
dx
para a qual encontramos, usando as mesmas condi¸˜es iniciais,
co
v = v0 − kx (2.26)
Portanto, a velocidade decresce linearmente com o deslocamento.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

13. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 59
E X E M P L O 2.5 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Encontre o deslocamento e a velocidade de uma part´
ıcula que se encontra em mo-
vimento vertical em um meio que tem uma for¸a de retardamento proporcional `
c a
velocidade.
Solu¸˜o: Considere uma part´
ca ıcula caindo com velocidade inicial v0 de uma altura h e campo
gravitacional constante (Figura 2.5). A equa¸˜o de movimento ´
ca e
dire¸˜o z
ca
dv
F =m = −mg − kmv (2.27)
dt
onde −kmv representa a for¸a positiva para cima desde z onde v = z no sentido positivo para cima,
c ˙
assim como o movimento para baixo - isto ´, v < 0, assim −kmv > 0. A partir da Equa¸˜o 2.27,
e ca
temos
dv
= −dt (2.28)
kv + g
Integrando a Equa¸˜o 2.28 e considerando v(t = 0) ≡ v0 , temos (notando que v0 < 0)
ca
1
ln(kv0 + g) = −t + c
k
kv + g = e−kt+kc
dz g kv0 + g −kt
v= =− + e (2.29)
dt k k
Integrando mais uma vez e calculando a constante no sentido z(t = 0) ≡ h, temos
gt kv0 + g
z =h− + (1 − e−kt ) (2.30)
k k2
FIGURA 2-5
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

14. 60 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
FIGURA 2-6
A Equa¸˜o 2.29 mostra que enquanto o tempo se torna muito longo, a velocidade se aproxima do
ca
valor limite −g/k; esta ´ chamada velocidade terminal, vt . A Equa¸˜o 2.27 resulta no mesmo
e ca
resultado, porque a for¸a desaparecer´ – e daqui nenhum acceleration mais adicional ocorrer´ –
c a a
quando v = −g/k. Se a velocidade inicial exceder a velocidade terminal em magnitude, ent˜o a
o corpo come¸a imediatamente a retardar para baixo e v aproxima-se da velocidade terminal
c
na dire¸˜o oposta. A Figura 2-6 ilustra estes resultados para velocidades descendentes (valores
ca
positivos).
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.6 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Em seguida, tratamos o movimento do proj´til em duas dimens˜es, primeiramente
e o
sem considerar a resistˆncia do ar. Deixe a velocidade do a¸aime do proj´til ser v0
e c e
e o ˆngulo de eleva¸˜o ser θ (Figura 2-7). Calcule o deslocamento, a velocidade, e o
a ca
alcance do proj´til.
e
FIGURA 2-7
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

15. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 61
Solu¸˜o: Usando F = mg , as componentes da for¸a tornam-se
ca c
dire¸˜o x
ca
0 = m¨ x (2.31a)
dire¸˜o y
ca
−mg = m¨
y (2.31b)
Desconsiderando a altura da arma, e assumindo x = y = 0 e t = 0. Ent˜o
a
x=0
¨
x = v0 cos θ
˙
x = v0 t cos θ (2.32)
e
y = −g
¨
y = −gt + v0 sin θ
˙
−gt2
y= + v0 t sin θ (2.33)
2
A velocidade e o deslocamento total como fun¸˜es do tempo s˜o encontrados por:
co a
v= x2 + y 2 = (v0 + g 2 t2 − 2v0 gt sin θ)1/2
˙ ˙ 2
(2.34)
e
1/2
g 2 t4
r= x2 + y 2 = v0 t2 +
2
− v0 gt3 sin θ (2.35)
4
Podemos encontrar o alcance determinando o valor de x quando o proj´til atinge o solo, isto ´ ,
e e
quando y = 0
−gt
y=t + v0 sin θ =0 (2.36)
2
Um valor de y = 0 ocorre para t = 0 e o outro para t = T .
−gT
+ v0 sin θ = 0
2
2v0 sin θ
T = (2.37)
g
O alcance R ´ encontrado a partir de
e
2
2v0
x(t = T ) = alcance = sin θ cos θ (2.38)
g
2
v0
R = alcance = sin 2θ (2.39)
g
Observe que o alcance m´ximo ocorre para θ = 45◦ .
a
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

16. 62 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Vamos usar algum n´mero atual nestes c´lculos. Os alem˜es usaram uma arma de longo
u a a
alcance nomeada Grande Cabina na Primeira Guerra Mundial que bombardeou Paris. O m´ ıssel
chegou a uma velocidade de 1, 450m/s. Encontre o alcance previsto, a altura m´xima do proj´til,
a e
e o tempo de vˆo do proj´til se θ = 55◦ . Temos v0 = 1, 450m/s e θ = 55o , assim (da Equa¸˜o 2.39)
o e ca
o alcance torna-se
(1450m/s)2
R= [sin (110o )] = 202km
9.8m/s2
a Grande Cabina atual alcan¸a 120km . A diferen¸a ´ um resultado do efeito real da resistˆncia
c c e e
do ar.
Para encontrar a altura m´xima atingida, precisamos calcular y para o tempo T /2 onde T ´
a e
o tempo de vˆo do proj´til:
o e
(2)(1450m/s)(sin 55o )
T = = 242s
9.8m/s2
T −gT 2 v0 T
ymax t = = + sin θ
2 8 2
−(9.8m/s)(242s)2 (1450m/s)(242s) sin (55o )
= +
8 2
= 72km
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.7 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
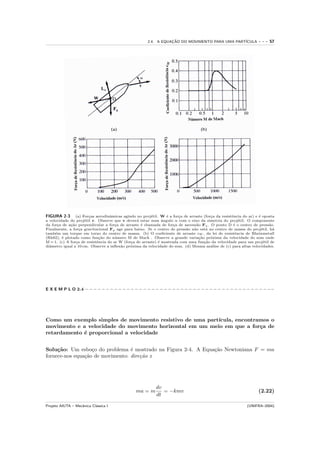
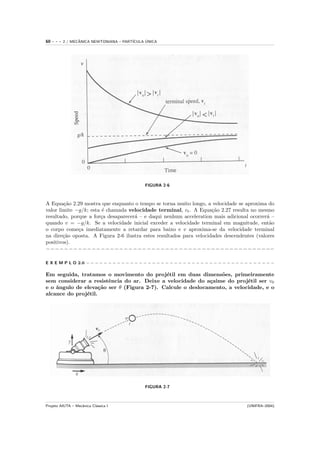
A seguir, adicionamos os efeitos da resistˆncia do ar no movimento do proj´til do
e e
exemplo anterior. Calcule o decrescimento do alcance deste supondo que a for¸a cau-
c
sada pela resistˆncia do ar seja diretamente proporcional ` velocidade do proj´til.
e a e
Solu¸˜o: As condi¸˜es iniciais s˜o as mesmas do exemplo anterior.
ca co a

x(t = 0) = 0 = y(t = 0)


x(t = 0) = v0 cos θ ≡ U
˙ (2.40)



y(t = 0) = v0 sin θ ≡ V
˙

Entretanto, as equa¸˜es do movimento, Equa¸˜o 2.31, torna-se
co ca
m¨ = −kmx
x ˙ (2.41)
m¨ = −kmy − mg
y ˙ (2.42)
A Equa¸˜o 2.41 ´ exatamente a mesma usada no Exemplo 2.4. A solu¸˜o ´, portanto
ca e ca e
U
x= (1 − e−kt ) (2.43)
k
Similarmente, a Equa¸˜o 2.42 ´ a mesma em rela¸˜o ` equa¸˜o do movimento no Exemplo 2.5.
ca e ca a ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

17. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 63
Podemos usar a solu¸˜o encontrada neste exemplo com a condi¸˜o de h = 0 (o fato que considera-
ca ca
mos a part´ıcula a ser projetada em declive no Exemplo 2.5 ´ de que n˜o h´ conseq¨ˆncia. O sinal
e a a ue
da velocidade inicial automaticamente leva isto ao c´lculo.) Portanto
a
gt kV + g
y=−
+ (1 − e−kt ) (2.44)
k k2
A trajet´ria ´ mostrada na Figura 2-8 por v´rios valores do retardamento da for¸a constante k que
o e a c
´ dado pelo vˆo do proj´til.
e o e
O alcance R , o qual ´ o alcance incluindo a resistˆncia do ar, pode ser encontrado previa-
e e
mente pelo calculo do tempo T requerido pela trajet´ria inteira e ent˜o, substituindo este valor na
o a
Equa¸˜o 2.43 por x. Este tempo T ´ encontrado previamente pela descoberta que t = T quando
ca e
y = 0. Da Equa¸˜o 2.44, encontramos
ca
kV + g
T = (1 − e−kt ) (2.45)
gk
Esta ´ uma equa¸˜o transcendental, e, portanto, n˜o podemos obter uma express˜o anal´
e ca a a ıtica para
T . Apesar de tudo n´s ainda temos m´todos poderosos para usar para solucionar tais problemas.
o e
FIGURA 2-8 As trajet´rias calculadas, da part´
o ıcula na resistˆncia do ar (Fres = −kmv) para v´rios valores de k ( nas
e a
unidades s−1 ). Os c´lculos foram apresentados para valores de θ = 60◦ e v0 = 600m/s. Os valores de y (Equa¸˜o 2.44)
a ca
s˜o marcados versus x (Equa¸˜o 2.43).
a ca
Apresentamos dois deles aqui: (1) o m´todo de perturba¸˜o para encontrar uma solu¸˜o apro-
e ca ca
ximada, e (2) o m´todo num´rico, o qual, pode normalmente ser constatado como o desejado.
e e
Compararemos os resultados.
M´todo de Perturba¸˜o. Para usar o m´todo de perturba¸˜o, encontramos um parˆmetro de
e ca e ca a
expans˜o ou uma fun¸˜o constante que ´ normalmente pequeno. No presente caso, este parˆmetro
a ca e a
´ o retardamento da constante k, porque j´ t´
e a ınhamos solucionado o presente problema com k = 0,
e agora poder´ıamos manter o retardamento da for¸a, mas deixar o k ser pequeno. Entretanto, se
c
expandirmos o termo exponencial da Equa¸˜o 2.45 (veja Equa¸˜o D.34 do Apˆndice D) na s´rie de
ca ca e e
for¸as com inten¸˜o de manter somente os termos mais baixos de k n , onde k ´ o nosso parˆmetro
c ca e a
de expans˜o.
a
kV + g 1 1
T = kT − k 2 T 2 + k 3 T 3 − ... (2.46)
gk 2 6
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

18. 64 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Se mantivermos somente termos na expans˜o atrav´s do k 3 , esta equa¸˜o pode ser reestruturada
a e ca
na forma
2V /g 1
T = + kT 2 (2.47)
1 + kV /g 3
Agora, temos o parˆmetro de expans˜o k no denominador do primeiro termo no lado direito da
a a
equa¸˜o. Precisamos expandir esse termo em uma s´rie de for¸as (S´ries de Taylor, ver Equa¸˜o
ca e c e ca
D.8 do Apˆndice D):
e
1
= 1 − (kV /g) + (kV /g)2 − ... (2.48)
1 + kV /g
Onde podemos manter somente temos atrav´s de k 2 , pois somente temos termos atrav´s de k na
e e
Equa¸˜o 2.47. Se inserirmos esta expans˜o da Equa¸˜o 2.48 no primeiro termo do lado direito da
ca a ca
Equa¸˜o 2.47 e mantermos somente os termos em k para primeira ordem, temos
ca
2V T2 2V 2
T = + − 2 k + O(k 2 ) (2.49)
g 3 g
No qual escolhemos excluir o O(k 2 ), os termos da orem k 2 e mais altos. No limite k → 0 (sem
resistˆncia do ar), a Equa¸˜o 2.49 nos mostra o mesmo resultado que no exemplo anterior:
e ca
2V 2v0 sin θ
T (k = 0) = T0 = =
g g
Entretanto, se k ´ pequeno (mas n˜o foi totalmente exclu´
e a ıdo) o tempo do vˆo ser´ aproximadamente
o a
igual a T0 . Ent˜o se usarmos este valor aproximado para T = T0 no lado direito da Equa¸˜o 2.49
a ca
teremos
2V kV
T ∼
= 1− (2.50)
g 3g
a qual ´ desejada uma express˜o aproximada para o tempo de vˆo.
e a o
A seguir escrevemos a equa¸˜o para x (Equa¸˜o 2.43) na forma expandida:
ca ca
U 1 1
x= kt − k 2 t2 + k 3 t3 − ... (2.51)
k 2 6
J´ que x(t = T ) ≡ R , temos aproximadamente para o alcance
a
1
R ∼ U T − kT 2
= (2.52)
2
onde, novamente, mantemos os termos somente atrav´s da primeira ordem do k. Agora podemos
e
avaliar esta express˜o pelo uso do valor de T da Equa¸˜o 2.50. Se mantermos somente os termos
a ca
lineares no k, encontramos
2U v 4kV
R ∼
= 1− (2.53)
g 3g
A quantidade 2U V /g agora pode ser escrita (usando as Equa¸˜es 2.40) como
co
2U v 2v 2 v2
= 0 sin θ cos θ = 0 sin 2θ = R (2.54)
g g g
As quais podem ser reconhecidas em rela¸˜o ao alcance R do proj´til quando a resistˆncia do ar ´
ca e e e
desprezada. Ent˜o
a
4kV
R ∼R 1−
= (2.55)
3g
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

19. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 65
Al´m dessa s´rie de valores de k podemos esperar que nosso m´todo de perturba¸˜o esteja correto?
e e e ca
Se olharmos a expans˜o na Equa¸˜o 2.48, vemos que a expans˜o n˜o ir´ convergir a n˜o ser que
a ca a a a a
kV /g < 1 ou k < g/V , e na verdade gostar´
ıamos que k << g/V = g/(v0 sin θ).
M´todo Num´rico. A Equa¸˜o 2.45 pode ser resolvida numericamente usando um computador
e e ca
por uma variedade de m´todos, estabelecemos a volta para solucionar a equa¸˜o para T por
e ca
muitos valores de k at´ 0, 08s−1 : Ti (ki ). Estes valores de T e k est˜o inseridos na Equa¸˜o 2.43
e a ca
para encontrar o alcance R , o qual ´ mostrado na Figura 2-9. O alcance decai rapidamente com
e
o aumento da resistˆncia do ar, exatamente como esperamos, mas n˜o ´ mostrada a dependˆncia
e a e e
linear sugerida pela solu¸˜o do m´todo de perturba¸˜o da Equa¸˜o 2.55.
ca e ca ca
Para o movimento do proj´til descrito nas Figuras 2-8 e 2-9, a aproxima¸˜o linear n˜o est´
e ca a a
constatada para os valores de k t˜o baixos quanto 0.01s−1 e incorretamente mostra que o alcance
a
´ zero para todos valores de k maiores do que 0.014s−1 . Esta desconcordˆncia com o m´todo
e a e
de perturba¸˜o n˜o ´ uma surpresa, pois o resultado linear para o alcance R era dependente
ca a e
em k << g/(v0 sin θ) = 0.02s−1 , o qual ´ dificilmente verdade at´ para o k = 0.01s−1 . Essa
e e
concordˆncia pode ser adequada para k = 0.005s−1 . Os resultados mostrados na Figura 2-8
a
indicam que para valores de k > 0.005s−1 , dificilmente a resistˆncia pode ser considerada numa
e
perturba¸˜o. De fato, para k > 0.01s−1 a resistˆncia torna-se valor dominante no movimento do
ca e
proj´til.
e
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
FIGURA 2-9 O valor de alcance calculado aproximadamente e numericamente para um dado proj´til ´ mostrado na
e e
Figura 2-8 e plotado como uma fun¸˜o da for¸a constante de retardamento k.
ca c
O exemplo anterior indica como o mundo real pode ser complicado. Neste exemplo, ainda
podemos fazer algumas suposi¸˜es n˜o f´
co a ısicas – assumindo por exemplo que a for¸a de retardamento
c
´ sempre linearmente proporcional a velocidade. Ent˜o nossos c´lculos num´ricos n˜o s˜o precisos,
e a a e a a
pois como mostra a Figura 2-3 a melhor suposi¸˜o pode ser incluir um termo retardat´rio v 2
ca o
conforme necess´rio. Da mesma forma adicionando termos podemos resolver dificuldades com o
a
c´lculo num´rico, e fazer um c´lculo similar no pr´ximo exemplo. Temos que incluir o arquivo
a e a o
do autor Matchcad para produzir as Figuras 2-8 e 2-9 no Apˆndice H para aqueles estudantes
e
poderem reproduzir os c´lculos. Enfatizamos que h´ muitas formas para a performance do c´lculo
a a a
num´rico com computadores, e o estudante ir´ provavelmente querer transformar n´meros com
e a u
praticidade.
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

20. 66 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
E X E M P L O 2.8 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Use os dados mostrados na Figura 2-3 para calcular a trajet´ria de um proj´til real.
o e
Suponha uma velocidade do a¸aime de 600m/s, a eleva¸˜o do injetor de 450 , e uma
c ca
massa do proj´til de 30kg. Trace em um plano a altura y versus a distˆncia horizontal
e a
x e trace y, x, e y versus o tempo com e sem resistˆncia do ar. Inclua somente a
˙ ˙ e
resistˆncia do ar e a gravidade, ignore outras for¸as poss´
e c ıveis tais como o elevador.
Solu¸˜o: Primeiramente, fa¸amos uma tabela da for¸a de retardamento versus a velocidade inter-
ca c c
pretando a Figura 2-3. Interprete a for¸a a cada 50m/s para a Figura 2-3c e a cada 100m/s para
c
a Figura 2-3d. Podemos ent˜o usar uma linha reta entre os valores tabular. Usemos o sistema de
a
coordenadas mostrado na Figura 2-7. A equa¸˜o do movimento torna-se
ca
Fx
x=−
¨ (2.56)
m
Fy
y=−
¨ −g (2.57)
m
onde Fx e Fy s˜o as for¸as de retardamento. Suponha que g ´ constante. Fx ser´ sempre um
a c e a
n´mero positivo, mas Fy > 0 para o proj´til que sobe, e Fy < 0 para o proj´til que desce. Deixe θ
u e e
ser o ˆngulo de eleva¸˜o dos proj´teis na horizontal em qualquer instante.
a ca e
v = x2 + y 2
˙ ˙ (2.58)
y˙
tan θ = (2.59)
x
˙
Fx = F cos θ (2.60)
Fy = F sin θ (2.61)
FIGURA 2-10 Os resultados do Exemplo 2.8. As linhas s´lidas s˜o os resultados se a resistˆncia do ar n˜o estiver
o a e a
inclu´
ıda, enquanto que as linhas tracejadas abrangem os resultados que incluem a for¸a de resistˆncia do ar. Em (a)
c e
tamb´m incluimos o efeito da densidade do ar causando uma pequena dependˆncia quando o proj´til sobe.
e e e
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

21. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 67
Podemos calcular Fx e Fy para qualquer instante sabendo x e y. Acima de um intervalo pequeno
˙ ˙
do tempo, x e y podem ser calculados.
˙ ˙
t
x =
˙ xdt + v0 cos θ
¨ (2.62)
0
t
y
˙ = y dt + v0 sin θ
¨ (2.63)
0
t
x = xdt
˙ (2.64)
0
t
y = ydt
˙ (2.65)
0
Escrevemos um programa de computador curto para conter nossa tabela para as for¸as de
c
retardamento e para executar os c´lculos para x, y, x, e y em fun¸˜o do tempo. Devemos calcular
a ˙ ˙ ca
as integrais para intervalos pequenos de tempo pois as for¸as s˜o dependentes do tempo. Figura
c a
2-10 mostra os resultados.
Observe a grande diferen¸a que a resistˆncia do ar faz. Na Figura 2-10a, a distˆncia horizontal
c e a
(escala) que o proj´til viaja ´ aproximadamente 16km comparados a quase 37km sem nenhuma
e e
resistˆncia do ar. Nosso c´lculo ignorou o fato que a densidade do ar depende da altura. Se
e a
fizermos exame da diminui¸˜o na densidade do ar com altura, obtemos a terceira curva com uma
ca
escala de 18km mostrados na Figura 2-10a. Se incluirmos tamb´m o elevador, a escala seria ainda
e
maior. Observe que a mudan¸a nas velocidades na Figura 2-10c e 2-10d espelham a for¸a resistiva
c c
do ar da Figura 2-3. O decr´scimo r´pido da velocidade ocorre at´ alcan¸ar a velocidade do som,
e a e c
e avalia ent˜o os n´
a ıveis de mudan¸a das velocidades um pouco fora.
c
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Isto conclui nossa subse¸˜o dos efeitos das for¸as de retardamento. Muito mais coisas pode-
ca c
riam ser feitas para incluir efeitos reais, mas o m´todo est´ desobstru´
e a ıdo. Normalmente, um efeito ´
e
adicionado para um tempo, e os resultados s˜o analisados antes que um outro efeito seja adicionado.
a
ˆ
OUTROS EXEMPLOS DA DINAMICA
Conclu´ımos esta se¸˜o com dois exemplos padr˜o adicionais do comportamento dinˆmico da
ca a a
part´
ıcula.
E X E M P L O 2.9 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
A M´quina de Atwood consiste em uma roldana lisa com dois corpos suspensos por
a
uma corda de massa desprez´ ıvel em cada ponta. Ache a acelera¸˜o dos corpos e a
ca
tens˜o na corda (a)quando a roldana est´ em repouso e (b) quando a roldana est´
a a a
dentro de um elevador descendo com acelera¸˜o constante α.
ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

22. 68 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
FIGURA 2-11
Solu¸˜o: Desprezamos a massa da corda e assumimos que a roldana est´ lisa – isto ´, n˜o tem
ca a e a
atrito com a corda. A tens˜o T deve ser a mesma por toda a corda. As equa¸˜es de movimento se
a co
transformam, para cada massa, para o caso (a),
m1 x1 = m1 g − T
¨ (2.66)
m2 x2 = m2 g − T
¨ (2.67)
Observe novamente a finalidade do conceito de for¸a: Precisamos apenas identificar as for¸as
c c
atuando em cada massa. A tens˜o T ´ a mesma em ambas equa¸˜es. Se a corda ´ inextens´
a e co e ıvel,
ent˜o x2 = −x1 , e as Equa¸˜es 2.66 e 2.67 podem ser combinadas
a ¨ ¨ co
m1 x1 = m1 g − (m2 g − m2 x2 )
¨ ¨
= m1 g − (m2 g + m2 x1 )
¨
Rearranjando,
g(m1 − m2 )
x1 =
¨ = −x2¨ (2.68)
m1 + m2
Se m1 > m2 , ent˜o x1 > 0, e x2 < 0. A tens˜o pode ser obtida das Equa¸˜es 2.68 e 2.66:
a ¨ ¨ a co
T = m1 g − m1 x1
¨
(m1 − m2 )
T = m1 g − m1 g
m1 + m2
2m1 m2 g
T = (2.69)
m1 + m2
Para o caso (b), no qual a roldana est´ em um elevador, o sistema de coordenadas com origens
a
no centro da roldana n˜o est´ longe de ser um sistema inercial. Precisamos de um sistema inercial
a a
com origem no topo do cabo do elevador (Figura 2-11b). As equa¸˜es de movimento no sistema
co
inercial (x1 = x1 + x1 , x2 = x2 + x2 ) s˜o
a
m1 x1 = m1 (¨1 + x1 ) = m1 g − T
¨ x ¨
m2 x2 = m2 (¨2 + x2 ) = m2 g − T
¨ x ¨
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

23. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 69

m1 x1 = m1 g − T − m1 x1 = m1 (g − α) − T 
¨ ¨
(2.70)
m2 x2 = m2 g − T − m2 x2 = m2 (g − α) − T
¨ ¨

onde x1 = x2 = α. Temos x2 = −¨1 , assim resolvemos para x1 eliminando-o antes
¨ ¨ ¨ x ¨
(m1 − m2 )
x1 = −¨2 = (g − α)
¨ x (2.71)
m1 + m2
e
2m1 m2 (g − α)
T = (2.72)
m1 + m2
Repare que os resultados para a tens˜o e a acelera¸˜o est˜o corretos se a acelera¸˜o da gravidade
a ca a ca
estiver reduzida da quantia de acelera¸˜o α do elevador. A altera¸˜o para um elevador ascendente
ca ca
deveria ser ´bvia.
o
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.10 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −−
No nosso ultimo exemplo revimos muitas equa¸˜es de movimento para uma part´
´ co ıcula,
examinamos o movimento da uma part´ ıcula como um campo eletromagn´tico. Con-
e
sidere uma part´ıcula carregada entrando na regi˜o do campo magn´tico uniforme
a e
B – por exemplo, o campo da terra – como mostra a Figura 2-12. Determine seu
subseq¨ ente movimento.
u
FIGURA 2-12
Solu¸˜o: Escolhendo o sistema de coordenadas cartesianas com seu eixo y paralelo ao campo
ca
magn´tico. Se q ´ a carga da part´
e e ıcula, v ´ sua velocidade, a sua acelera¸˜o e B o campo magn´tico
e ca e
da Terra, ent˜o:
a
v = xi + yj + zk
˙ ˙ ˙
a = xi + y j + z k
¨ ¨ ¨
B = B0 j
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

24. 70 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
A for¸a magn´tica F = qv × B = ma, assim
c e
m(¨i + y j + z k) = q(xi + yj + zk) × B0 j = qB0 (xk − zi)
x ¨ ¨ ˙ ˙ ˙ ˙ ˙
Igualando, as componentes vetoriais fornecem

m¨ = −qB0 z 
x ˙


m¨ = 0
y (2.73)



m¨ = qB0 x
z ˙

Integrando a segunda destas equa¸˜es, m¨ = 0 temos:
co y
y = y0
˙ ˙
Onde y0 ´ uma constante e ´ o valor inicial de y. Integrando a segunda em fun¸˜o do tempo,
˙ e e ˙ ca
fornece:
y = y0 t + y0
˙
onde y0 tamb´m ´ uma constante.
e e
Para integrar a 1o e a ultima equa¸˜o da Equa¸˜o 2.73, admitimos α = qB0 /m, assim ent˜o
´ ca ca a
x = −αz
¨ ˙
(2.74)
z = αx
¨ ˙
Estas duas simultˆneas equa¸˜es diferenciais podem facilmente ser desembreadas por uma diferen-
a co
cia¸˜o e substituindo na outra, fornecendo
ca
...
z = α¨ = −α2 z
x ˙
...
x = −α¨ = −α2 x
z ˙
assim ent˜o
a
... 
z = −α2 z 
˙
... (2.75)
x = −α2 x
˙
Ambas destas equa¸˜es diferenciais tˆm-se a mesma forma de solu¸˜o. Usando a t´cnica do exemplo
co e ca e
C.2 do apˆndice C, temos
e
x = A cos αt + B sin αt + x0
z = A cos αt + B sin αt + z0
Onde A,A ,B,B , x0 e z0 s˜o constantes de integra¸˜o que s˜o determinadas pela posi¸˜o inicial e
a ca a ca
velocidade da part´
ıcula e pelas equa¸˜es de movimento, Equa¸˜o 2.74. Estas solu¸˜es podem ser
co ca co
reescritas

(x − x0 ) = A cos αt + B sin αt 



(y − y0 ) = y0 t
˙ (2.76)



(z − z0 ) = A cos αt + B sin αt

As coordenadas x e z s˜o relacionadas pela Equa¸˜o 2.74, assim substituindo as Equa¸˜es ?? na
a ca co
primeira equa¸˜o da Equa¸˜o 2.74 determinando
ca ca
−α2 A cos αt − α2 B sin αt = −α(−αA sin αt + B cos αt) (2.77)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

25. 2.4. A EQUACAO DO MOVIMENTO PARA UMA PART´
¸˜ ICULA --- 71
Porque a Equa¸˜o 2.77 ´ v´lida para todo t, em particular t = 0 e t = π/2α, Equa¸˜o 2.77 produz
ca e a ca
−α2 A = −α2 B
que ´
e
A=B
e
−α2 B = α2 A
fornece
B = −A
n´s agora temos
o

(x − x0 ) = A cos αt + B sin αt 


(y − y0 ) = y0 t
˙ (2.78)



(z − z0 ) = −B cos αt + A sin αt

se t = 0, z = z0 e x = 0, ent˜o da Equa¸˜o 2.78, diferenciando e armando t = 0, fornece
˙ ˙ ˙ a ca
αB = 0
e
αA = z0
˙
ent˜o
a
z0
˙
(x − x0 ) = cos αt
α
(y − y0 ) = y0 t
˙
z0
˙
(z − z0 ) = sin αt
α
Finalmente, 
z0 m
˙ qB0 t
x − x0 = cos 

qB0 m






(y − y0 ) = y0 t
˙ (2.79)



z0 m
˙ qB0 t 

z − z0 = sin



qB0 m
Estas s˜o equa¸˜es parametrizadas da h´lice circular de raio z0 m/qB0 . Assim, o mais r´pido que a
a co e ˙ a
part´ıcula entra no campo ou a maior massa, o lado do raio da h´lice. E a maior carga da part´
e ıcula
ou o mais forte campo magn´tico, e pequena h´lice. Note tamb´m como a part´
e e e ıcula carregada
´ capturada pelo campo magn´tico - justamente flutuando ao longo da dire¸˜o do campo. Neste
e e ca
exemplo, a part´ ıcula n˜o tem nenhuma componente inicial da velocidade ao longo do eixo x, mas
a
mesmo se tivesse ela n˜o flutuaria ao longo do eixo (veja problema 2-31). Finalmente, note que a
a
for¸a magn´tica da part´
c e ıcula sempre atua perpendicular a uma velocidade e desde j´ n˜o pode ser
a a
acelerada. A Equa¸˜o 2.79 verifica este fato.
ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

26. 72 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
O campo magn´tico da Terra n˜o ´ t˜o simples quanto o campo uniforme deste exemplo. No
e a e a
entanto este exemplo fornece uma percep¸˜o de um dos mecanismos pelo qual o campo magn´tico
ca e
da terra prende raios c´smicos de baixa energia e o vento solar para criar zonas de Van Allen.
o
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2.5 ¸˜
TEOREMAS DE CONSERVACAO
Agora retornamos a uma discuss˜o detalhada da mecˆnica Newtoniana de uma unica part´
a a ´ ıcula
para derivar-mos teoremas importantes quanto a grandezas conservativas. Devemos enfatizar que
n˜o estamos provando a conserva¸˜o de v´rias grandezas. Estamos simplesmente deduzindo as
a ca a
consequˆncias das leis de Newton na dinˆmica. Estas implica¸˜es podem ser testadas em experi-
e a co
mentos e suas verifica¸˜es ent˜o podem confirmar as leis da dinˆmica. O fato ´ que esses teoremas
co a a e
de conserva¸˜o tˆm realmente sido v´lidos em muitos exemplos e fornecem uma importante prova
ca e a
da exatid˜o das leis de Newton, pelo menos na f´
a ısica cl´ssica.
a
O primeiro teorema de conserva¸˜o de interesse ´ o momento linear de uma part´
ca e ıcula. Se
a part´
ıcula ´ livre, isto ´, se a part´
e e ıcula n˜o est´ sujeita a nenhuma for¸a, ent˜o a Equa¸˜o 2.2
a a c a ca
fica simplesmente p = 0. Portanto, p ´ um vetor constante no tempo, e o primeiro teorema de
˙ e
conserva¸˜o ´
ca e
I. O momento linear total p da part´
ıcula ´ conservado quando a for¸a total ´ zero.
e c e
Observe que este resultado ´ derivado de uma equa¸˜o vetorial, p = 0, e portanto ´ aplicada
e ca ˙ e
para cada componente do momento linear. Para expressar o resultado de outra forma, seja s algum
vetor constante tal que F · s = 0, independente do tempo.
Ent˜o
a
p·s=F·s=0
˙
ou, integrando com rela¸˜o ao tempo,
ca
p · s = constante (2.80)
o qual afirma que o componente do momento linear na dire¸˜o em que a for¸a torna-se nulo, ´
ca c e
constante no tempo.
O momento angular L de uma part´ ıcula com rela¸˜o a origem, da qual um vetor posi¸˜o
ca ca
r ´ medido, ´ definido por
e e
L≡r×p (2.81)
O torque ou o momento de uma for¸a N com rela¸˜o a mesma origem, ´ definido como
c ca e
N≡r×F (2.82)
onde r ´ o vetor posi¸˜o da origem at´ o ponto onde a for¸a F ´ aplicada. Como F = mv para a
e ca e c e ˙
part´
ıcula, o torque torna-se
N = r × mv = r × p
˙ ˙
Agora
˙ d
L = (r × p) = (˙ × p) + (r × p)
r ˙
dt
mas
r × p = r × mv = m(˙ × r) ≡ 0
˙ ˙ r ˙
ent˜o
a
˙
L=r×p=N
˙ (2.83)
Se n˜o h´ torque agindo na part´
a a a ˙
ıcula (isto ´, se N = 0), ent˜o L = 0 e L ´ um vetor constante no
e e
tempo. O segundo teorema importante da conserva¸˜o ´
ca e
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

27. ¸˜
2.5. TEOREMAS DE CONSERVACAO --- 73
II. O momento angular de uma part´
ıcula n˜o sujeita a torque ´ conservada.
a e
Lembramos que o estudante que uma escolha criteriosa da origem de um sistema de coorde-
nadas frequentemente possibilitar´ que um problema seja resolvido muito mais facilmente do que
a
uma escolha da origem de forma casual. Por exemplo, o torque ser´ zero no sistema de coordenadas
a
cujo centro est´ localizado na dire¸˜o da resultante da for¸a. O momento angular ser´ conservado
a ca c a
nesse caso.
Se o trabalho realizado sobre uma part´ ıcula por uma for¸a F transformando a part´
c ıcula de
uma Condi¸˜o 1 para a Condi¸˜o 2, ent˜o este trabalho ´ definido como sendo
ca ca a e
2
W12 ≡ F · dr (2.84)
1
Se F ´ a for¸a resultante l´
e c ıquida agindo na part´
ıcula,
dv dr dv
F · dr = m · dt = m · vdt
dt dt dt
m d m d 2
= (v · v)dt = (v )dt = d( 1 mv 2 )
2 (2.85)
2 dt 2 dt
A integra¸˜o da Equa¸˜o 2.84 ´, assim, uma diferencial exata, e o trabalho feito pela for¸a total F
ca ca e c
agindo na part´
ıcula ´ igual a varia¸˜o da sua energia cin´tica:
e ca e
2
W12 = ( 2 mv 2 )
1 2 2
= 1 m(v2 − v1 ) = T2 − T1
2 (2.86)
1
1
onde T ≡ 2 mv 2 ´ a energia cin´tica da part´
e e ıcula. Se T1 > T2 ent˜o W12 < 0, a part´
a ıcula realiza
e e ´
trabalho resultando no decr´scimo de sua energia cin´tica. E importante ressaltar que a for¸a F c
da Equa¸˜o 2.85 ´ a for¸a total (isto ´, resultante l´
ca e c e ıquida das for¸as) sobre a part´
c ıcula.
Vamos agora examinar a integral que aparece na Equa¸˜o 2.84 de um ponto de vista diferente.
ca
Em muitos problemas f´ ısicos, a for¸a F tem a propriedade que o trabalho requerido para mover a
c
part´
ıcula de uma posi¸˜o para outra sem nenhuma mudan¸a na energia cin´tica depende somente
ca c e
da posi¸˜o inicial e final e n˜o da trajet´ria tomada pela part´
ca a o ıcula. Por exemplo, assumindo o
trabalho feito para mudar a part´ ıcula do ponto 1, na Figura 2-13, para o ponto 2 ´ independente das
e
trajet´rias reais a, b ou c. Esta propriedade ´ demonstrada, por exemplo, pelo campo gravitacional
o e
constante. Assim, se a part´ ıcula de massa m ´ levantada por uma altura h (por qualquer trajet´ria),
e o
ent˜o um trabalho mgh foi realizado sobre a part´
a ıcula, e a part´
ıcula pode fazer um trabalho igual
retornando para a sua posi¸˜o original.
ca
FIGURA 2-13
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

28. 74 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Esta capacidade de realizar trabalho ´ chamada energia potencial da part´
e ıcula.
Podemos definir a energia potencial da part´ıcula em termos do trabalho (feito pela for¸a F)
c
requerido para transportar a part´ıcula de um ponto 1 para um ponto 2 (sem troca l´ ıquida na
energia cin´tica):
e
2
F · dr = U1 − U2 (2.87)
1
O trabalho feito para mover a part´ ıcula ´ simplesmente a diferen¸a na energia potencial U nos
e c
dois pontos. Por exemplo, se levantamos uma maleta de uma posi¸˜o 1 no ch˜o at´ uma posi¸˜o
ca a e ca
2 sob uma mesa, n´s como agente externo realizamos trabalho contra a for¸a da gravidade. Seja
o c
a for¸a F da Equa¸˜o 2.87 a for¸a da gravidade, quando levantamos a maleta, F · dr se torna
c ca c
negativo. O resultado da integra¸˜o na Equa¸˜o 2.87 ´ U2 − U1 negativo, ent˜o a energia potencial
ca ca e a
na posi¸˜o 2 sob a mesa ´ maior que a da posi¸˜o 1 no ch˜o. A mudan¸a na energia potencial
ca e ca a c
U2 −U1 ´ o negativo do trabalho feito pela for¸a gravitacional, como pode ser visto multiplicando-se
e c
ambos os lados da Equa¸˜o 2.87 por −1. Como agente externo, fazemos trabalho positivo (contra
ca
a gravidade) para elevar a energia potencial da maleta.
A Equa¸˜o 2.87 pode ser reproduzida∗ se escrevemos F como gradiente da fun¸˜o escalar U :
ca ca
F = −grad U = − U (2.88)
Ent˜o
a
2 2 2
F · dr = − ( U ) · dr = − dU = U1 − U2 (2.89)
1 1 1
Na maioria dos sistemas de interesse, a energia potencial ´ fun¸˜o da posi¸˜o e, possivelmente,
e ca ca
do tempo: U = U (r) ou U = U (r, t). N˜o consideramos casos em que a energia potencial ´ fun¸˜o
a e ca
da velocidade† .
´
E importante perceber que a energia potencial ´ definida apenas dentro de uma constante
e
aditiva; isto ´, a for¸a definida por − U n˜o ´ diferente daquela definida por − (U + constante).
e c a e
Portanto a energia potencial n˜o tem um significado absoluto; apenas diferen¸as de energia poten-
a c
cial s˜o fisicamente significativas (como na Equa¸˜o 2.87).
a ca
Se escolhemos um certo sistema de referˆncia inercial para descrever um processo mecˆnico,
e a
as leis do movimento s˜o as mesmas como em qualquer outro sistema de referˆncia em movimento
a e
uniforme relativo ao sistema de referˆncia original. A velocidade de uma part´
e ıcula ´ em geral
e
diferente dependendo de qual sistema de referˆncia inercial escolhemos como base para descrever
e
o movimento. Ent˜o achamos que ´ imposs´ atribuir uma energia cin´tica absoluta para uma
a e ıvel e
part´ıcula do mesmo jeito que ´ imposs´ atribuir um significado absoluto para a energia potencial.
e ıvel
Ambas limita¸˜es s˜o resultado do fato que a escolha de uma origem do sistema de coordenadas
co a
usada para descrever processos f´ ısicos ´ sempre arbitr´ria. James Clerk Maxwell (1831 - 1879)
e a
resumiu a situa¸˜o como sendo‡ :
ca
Devemos, portanto, considerar a energia de um sistema material como a grandeza
a que devemos determinar o acr´scimo ou diminui¸˜o enquanto o sistema passa de
e ca
uma condi¸˜o definida a outra. O valor absoluto de energia na condi¸˜o padr˜o ´
ca ca a e
desconhecida por n´s, e isso n˜o teria importˆncia se fosse conhecida, como todos
o a a
fenˆmenos dependem da varia¸˜o de energia e n˜o de seu valor absoluto.
o ca a
Agora, definimos a energia total de uma part´
ıcula como a soma das energias cin´tica e
e
potencial:
E ≡T +U (2.90)
∗ A condi¸˜o necess´ria e suficiente que permite uma fun¸˜o vetorial ser representada pelo gradiente de uma
ca a ca
fun¸˜o escalar ´ que o rotacional da fun¸˜o vetorial se anule identicamente.
ca e ca
† Potenciais dependentes da velocidade s˜o necess´rios em certas situa¸˜es, e.g., no eletromagnetismo (os cha-
a a co
mados potenciais de Li´nard-Wiechert)
e
‡ J. C. Maxwell, Matter and Motion (Cambridge, 1877), p.91.
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

29. ¸˜
2.5. TEOREMAS DE CONSERVACAO --- 75
A derivada total na vari´vel tempo de E ´
a e
dE dT dU
= + (2.91)
dt dt dt
Para obter as derivadas temporais que aparecem ` direita da equa¸˜o, primeiro notemos que a
a ca
Equa¸˜o 2.85 pode ser escrita como:
ca
1
F · dr = d( mv 2 ) = dT (2.92)
2
Dividindo por dt,
dT dr
=F· =F·r
˙ (2.93)
dt dt
Temos tamb´m
e
dU ∂U dxi ∂U
= +
dt i
∂xi dt ∂t
∂U ∂U
= xi +
˙
i
∂xi ∂t
∂U
= ( U) · r +
˙ (2.94)
∂t
Substituindo as Equa¸˜es 2.93 e 2.94 na 2.91, encontramos
co
dE ∂U
= F · r + ( U) · r +
˙ ˙
dt ∂t
∂U
= (F + U ) · r +
˙
∂t
∂U
= (2.95)
∂t
como o termo F + U desaparece em visto da defini¸˜o de energia potencial (Equa¸˜o 2.88) se a
ca ca
for¸a total for uma for¸a conservativa F = − U .
c c
Se U n˜o for uma fun¸˜o expl´
a ca ıcita do tempo (i.e., se ∂U/∂t = 0; lembre que n˜o consideramos
a
potenciais dependentes da velocidade), o campo de for¸a representado por F ´ conservativo. Sob
c e
estas condi¸˜es temos o terceiro teorema importante da conserva¸˜o:
co ca
III. A energia total E de uma part´
ıcula em um campo de for¸as conservativo ´ constante no
c e
tempo.
Deve ser repetido que n˜o provamos as leis de conserva¸˜o do momento linear, momento
a ca
angular, e energia. Apenas derivamos v´rias consequˆncias das leis de Newton; isto ´, se estas leis
a e e
s˜o v´lidas em uma certa situa¸˜o, ent˜o momento e energia ser˜o conservados. Mas nos tornamos
a a ca a a
t˜o apaixonados por estes teoremas de conserva¸˜o que os elevamos ao n´ de leis e insistimos
a ca ıvel
que eles s˜o v´lidos em qualquer teoria f´
a a ısica, at´ mesmo aquelas aplicadas a situa¸˜es em que a
e co
mecˆnica Newtoniana n˜o ´ v´lida, como por exemplo, na intera¸˜o de cargas em movimento ou em
a a e a ca
sistemas de mecˆnica quˆntica. Ainda n˜o temos leis de conserva¸˜o para estas situa¸˜es, mas sim
a a a ca co
postulados da conserva¸˜o que for¸amos sobre a teoria. Por, exemplo, se temos duas cargas el´tricas
ca c e
isoladas em movimento, as for¸as eletromagn´ticas entre elas n˜o s˜o conservativas. Portanto,
c e a a
dotamos o campo eletromagn´tico de uma certa quantidade de energia para que a conserva¸˜o de
e ca
energia seja v´lida. Este procedimento ´ satisfat´rio apenas se as consequˆncias n˜o contradizem
a e o e a
nenhum fato experimental, e este ´ o caso das cargas em movimento. Ent˜o estendemos o conceito
e a
usual de energia para incluir “energia eletromagn´tica” e satisfazer nossa pr´-concebida no¸˜o de
e e ca
que a energia deve ser conservada. Pode parecer um arbitr´rio e dr´stico passo a se dar, mas nada,
a a
que foi dito, sucedeu com tanto sucesso, e estas “leis” da conserva¸˜o foram o mais bem sucedido
ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

30. 76 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
conjunto de princ´ıpios da f´
ısica. A recusa em abandonar a conserva¸˜o de energia e momento
ca
levaram Wolfgang Pauli (1900-1958) a postular em 1930 a existˆncia do neutrino para ajustar as
e
˜
contas que nAo “fechavam” para energia e momento no decaimento radiativo β. Este postulado
permitiu a Enrico Fermi (1901 - 1954) construir uma grande teoria do decaimento β em 1934,
mas a observa¸˜o direta do neutrino n˜o foi feita at´ 1953, quando Reines e Cowan realizaram seu
ca a e
famoso experimento∗ . Aderindo a convic¸˜o que energia e momento devem ser conservados, uma
ca
nova part´
ıcula elementar foi descoberta, que ´ de grande importˆncia nas teorias modernas....
e a
E X E M P L O 2.11−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Um ratinho de massa “m” joga-se sobre a borda externa de uma p´ de um ventilador
a
de teto girando livremente com momento de in´rcia “I” e raio “R”. De qual raz˜o ´
e a e
alterada a velocidade angular?
Solu¸˜o: O momento angular deve ser conservado durante o processo. Usaremos o conceito
ca
de momento de in´rcia aprendido na f´
e ısica elementar para relacionar momento angular L com a
velocidade angular ω : L = Iω. O momento angular inicial L0 = Iω0 deve ser igual ao momento
angular L (ventilador mais ratinho) ap´s o ratinho ter se jogado sobre o ventilador. A velocidade
o
da borda externa da p´ ´ v = ωR.
ae
v
L = Iω + mvR = (I + mR2 )
R
L = L0 = Iω0
v v0
(I + mR2 ) = I
R R
v I
=
v0 I + mR2
e
ω I
=
ω0 I + mR2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2.6 ENERGIA
O conceito de energia era mais popular na ´poca de Newton que atualmente. Mais tarde estu-
e
daremos duas novas formula¸˜es da dinˆmica, diferentes da de Newton e baseada na energia – o
co a
m´todo Lagrangiano e o Hamiltoniano.
e
Por volta do s´culo XIX, tornou-se claro que o calor era outra forma de energia e n˜o uma
e a
forma de fluido(chamado “cal´rico”) que fluia entre corpos quente e frio. Conde Rumford† , a quem
o
´ dado o cr´dito, que a grande quantidae de alor gerada na perfura¸˜o dos canh˜es era causada
e e ca o
pelo atrito e n˜o pelo chamado cal´rico. A energia produzida pelo atrito ´ apenas ´ a energia
a o e e
calor´
ıfica, troc´vel com a energia mecˆnica, e assim a conserva¸˜o total de energia ´ satisfeita.
a a ca e
∗ C.
L. Cowan, F. Reines, F. B. Harrison, H. W. Kruse, e A. D. McGuire, Science, 124, 103 (1956).
† Benjamim Thompson (1753 - 1814) nascido em Massachusetts e emigrado para Europa em 1776 como um
ref´gio legalista. Em meio as atividades deste militar destacado e, depois, na carreira cient´
u ıfica, ele superviosonou
a perfura¸˜o dos canh˜es como chefe do departamento de guerra da Bavaria
ca o
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

31. 2.6. ENERGIA --- 77
Por todo o s´culo XIX, cientistas realizaram experimentos sobre conserva¸˜o de energia,
e ca
resultando na importˆncia que ela tem atualmente. Hermann von Helmholtz (1821 - 1894) formulou
a
a lei geral da conserva¸˜o de energia em 1847. Baseado na conclus˜o do experimento calorim´trico
ca a e
de James Perscott Joule (1818 - 1889) que iniciou em 1840.
Considere uma part´ ıcula pontual sob influˆncia de uma for¸a conservativa com potencial U .
e c
A conserva¸˜o de energia (na realidade, energia mecˆnica, para ser exato neste caso) est´ refletida
ca a a
na Equa¸˜o 2.90.
ca
1
E = T + U = mv 2 + U (x) (2.96)
2
onde consideramos somente o caso unidimensional. Podemos reescrever a Equa¸˜o 2.96 como
ca
dx 2
v(t) = =± [E − U (x)] (2.97)
dt m
e integrando
x
±dx
t − t0 = (2.98)
2
x0
m [E − U (x)]
onde x = x0 e t = t0 . Temos formalmente a solu¸˜o para o caso unidimensional na Equa¸˜o 2.98;
ca ca
isto ´, encontramos x(t). Todo o restante ´ inserido no potencial U (x) da Equa¸˜o 2.98 e integrado,
e e ca
usando c´lculos num´ricos se necess´rio. Estudaremos mais adiante com alguns detalhes o potencial
a e a
1
U = 2 kx2 para oscila¸˜es harmˆnicas e U = −k/x para a for¸a gravitacional.
co o c
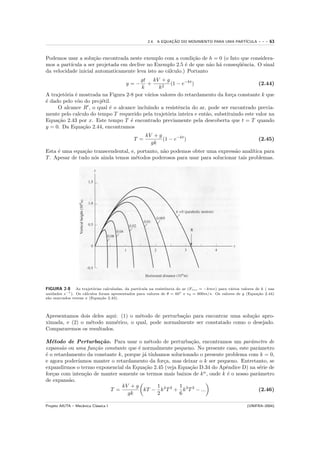
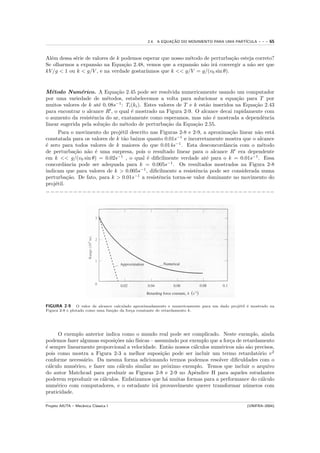
Podemos ter uma boa id´ia a respeito do movimento de uma unica part´
e ´ ıcula examinando o
gr´fico de um exemplo de U (x) conforme mostra a Figura 2-14. Primeiro, nota-se que, devido
a
a 1 mv 2 = T ≥ 0, E ≥ U (x), para algum movimento f´
2 ısico real. Vˆ-se na Figura 2-14 que o
e
movimento ´ ligado∗ para as energias E1 e E2 . Para E1 , o movimento ´ peri´dico, entre os pontos
e e o
de retorno xa e xb . Similarmente, para E2 o movimento tamb´m ´ peri´dico, por´m h´ duas
e e o e a
poss´ıveis regi˜es: xc ≤ x ≤ xd e xe ≤ x ≤ xf . A part´
o ıcula n˜o pode “saltar” de uma “cavidade”
a
para outra; uma vez numa cavidade, a part´ ıcula permanecer´ nela para sempre se a a sua energia
a
for sempre E2 . O movimento para uma part´ ıcula com energia E0 tem um unico valor, x = x0 . A
´
part´ıcula est´ em repouso com T = T0 [E0 = U (x0 )].
a
O movimento para a part´ ıcula de energia E3 ´ simples: a part´
e ıcula vem do infinito, p´ra a
em x = xg e retorna para o infinito–muito semelhante a uma bola de tˆnis arremessada contra
e
uma parede. Para a energia E4 , o movimento ´ n˜o-ligado e a part´
e a ıcula pode estar em qualquer
posi¸˜o. Sua velocidade mudar´ conforme se movimenta porque depende da diferen¸a entre E4
ca a c
e U (x). Se a part´ ıcula se move para a direita, sua velocidade aumentatar´ e dimunuir´ mas
a a
continuar´ movendo-se para o infinito.
a
O movimento da part´ ıcula E1 ´ semelhante ao de uma massa presa a uma mola. O potencial
e
na regi˜o xa < x < xb pode ser aproximadamente U (x) = 1 k(x − x0 )2 . Uma part´
a 2 ıcula com energia
em torno de E0 oscilar´ quase no ponto x = x0 . Estes pontos s˜o como um ponto de equil´
a a ıbrio,
porque a part´ ıcula est´ no ponto x = x0 ela permanecer´ ali. O equil´
a a ıbrio pode ser est´vel, inst´vel
a a
ou neutro. O unico equil´
´ ıbrio examinado ´ o est´vel porque se a part´
e a ıcula est´ localizada na regi˜o
a a
onde x = x0 dever´ finalmente retornar ao ponto. Podemos usar uma tigela esf´ricae e uma uma
a e
bolinha de a¸o como um exemplo. Com a tigela na su posi¸˜o natural, a bola pode rolar de um
c ca
ponto a outro no interior da tigela; mas finalemente ficar´ em repouso na sua base–em outros
a
termos, h´ um equil´
a ıbrio est´vel. Se virarmos a tigela com borda superior para baixo e colocar
a
a bola precisamente em de x = x0 (no topo da tigela), a bola estar´ em equil´ a ıbrio. Se a bola
estiver localizada liegiramente fora do ponto x = x0 , ela rola para fora (descer´!!); chamamos este
a
equil´ıbrio de inst´vel. O equil´
a ıbrio neutro ´ observado quando a bola estiver rolando sobre um
e
plano polido, numa superf´ horizontal.
ıcie
Em geral, podemos expressar o potencial U (x) em s´ries de Taylor em torno do ponto de
e
equil´ıbrio. Por simplicidade, assumimos o ponto de equil´ ıbrio para x = 0 em x = x0 (se n˜o, a
∗ N.T.: ligado aqui significa confinado a uma certa regi˜o do espa¸o.
a c
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

32. 78 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
FIGURA 2-14
podemos redefinir o sistema de coordenadas para obtˆ-lo). Ent˜o temos
e a
dU x2 d2 U x3 d3 U
U (x) = U0 + x + + + ... (2.99)
dx 2! dx2 3! dx3
0 0 0
O subscrito zero indica que esta grandeza est´ sendo calculada em x = 0. A energia potencial
a
U0 para x = 0 ´ simplesmente uma constante que podemos definir como sendo zero sem que haja
e
qualquer tipo de perda ou generaliza¸˜o. Se x = 0 ´ um ponto de equil´
ca e ıbrio, ent˜o
a
dU
=0 Ponto de Equil´
ıbrio (2.100)
dx
0
e a Equa¸˜o 2.99 fica
ca
x2 d2 U x3 d3 U
U (x) = + + ... (2.101)
2! dx2 3! dx3
0 0
Pr´ximo ao ponto de equil´
o ıbrio x = 0, o valor do x ´ pequeno, e cada termo na Equa¸˜o 2.101 ´
e ca e
muito menor do que o anterior. Por essa raz˜o, pegamos somente o primeiro termo na Equa¸˜o 2.101:
a ca
x2 d2 U
U (x) = (2.102)
2 dx2 0
ıbrio em x = 0 ´ est´vel ou inst´vel examinando o termo (d2 U/dx2 )0 .
Podemos determinar se o equil´ e a a
Se o x = 0 o equil´
ıbrio ´ est´vel, U (x) deve ser maior (mais positivo) no outro lado de x = 0.
e a
Como x2 ´ sempre positivo, as condi¸˜es para o equil´
e co ıbrio s˜o
a
d2 U
>0 Equil´
ıbrio Est´vel
a
dx2 0
(2.103)
d2 U
<0 Equil´
ıbrio Inst´vel
a
dx2 0
Caso (d2 U/dx2 )0 for zero, os termos de ordem superior devem ser examinados(ver Problema 2-45
e 2-46).
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

33. 2.6. ENERGIA --- 79
E X E M P L O 2.12 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
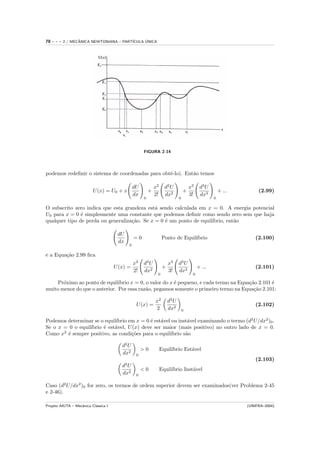
Considerando um sistema de roldanas, massas e fios finos apresentado na Figura 2-15.
Um fio de comprimento b ´ fixado no ponto A, passando sobre uma roldana no ponto
e
B localizada a uma distˆncia 2d , e finalmente liga-se na massa m1 . Outra roldana com
a
massa m2 ´ fixada passando sobre o fio, puxando-o para baixo entre A e B. Calcule a
e
distˆncia x1 quando o sistema est´ em equil´
a a ıbrio e determine se o equil´
ıbrio ´ est´vel
e a
ou n˜o. Essas roldanas n˜o possuem massa.
a a
Solu¸˜o: Podemos resolver este exemplo usando for¸as (i. e., quando x1 = 0 = x1 ) ou energia.
ca c ¨ ˙
Escolhemos o m´todo da energia, porque em equil´
e ıbrio a energia cin´tica ´ zero e necessitamos
e e
quantificar somente com a energia potencial quando a Equa¸˜o 2.100 ´ aplicada.
ca e
Admitindo U = 0 ao longo da linha AB.
U = −m1 gx1 − m2 g(x2 + c) (2.104)
Assumindo que a polia que suporta a massa m2 ´ pequena, ent˜o podemos ignorar o raio. A
e a
distˆncia c na Figura 2-15 ´ constante.
a e
x2 = [(b − x1 )2 /4] − d2
U = −m1 gx1 − m2 g [(b − x1 )2 /4] − d2 − m2 gc
FIGURA 2-15
ca ca ıbrio (x1 )0 ≡ x0 :
Por determina¸˜o dU/dx1 = 0, podemos determinar a posi¸˜o de equil´
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

34. 80 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
dU m2 g(b − x0 )
= −m1 g + =0
dx1 0 4 [(b − x1 )2 /4] − d2
4m1 [(b − x1 )2 /4] − d2 = m2 (b − x0 )
(b − x0 )2 (4m2 − m2 ) = 16m2 d2
1 2 1
4m1 d
x0 = b − (2.105)
4m2 − m2
1 2
Note que a real solu¸˜o existe somente quando 4m2 > m2 .
ca 1 2
Sob quais circunstˆncias a massa m2 ir´ puxar m1 at´ a polia B (i. e., x1 = 0)? Podemos
a a e
usar a Equa¸˜o 2.103 para determinar se o equil´
ca ıbrio ´ est´vel ou n˜o:
e a a
d2 U −m2 g m2 g(b − x1 )2
2 = +
dx1 4{[(b − x1 )2 /4] − d2 }1/2 16{[(b − x1 )2 /4] − d2 }3/2
Agora insira x1 = x0 .
d2 U g(4m2 − m2 )3/2
1 2
=
dx21 0 4m2 d
2
A condi¸˜o para o equil´
ca ıbrio (movimento real) previamente foi para 4m2 > m2 , ent˜o o equil´
1 2 a ıbrio,
quando ele existe, ser´ est´vel, porque (d2 U/dx2 )0 > 0.
a a
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
E X E M P L O 2.13 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
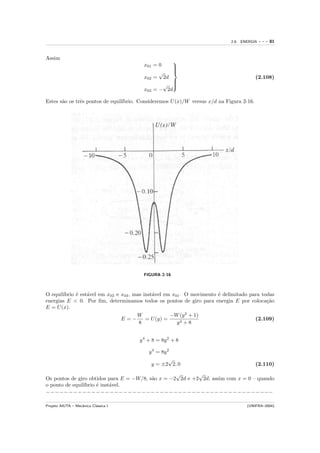
Considere um potencial unidimensional
−Wd2 (x2 + d2 )
U(x) = (2.106)
x4 + 8d4
´
Trace o potencial e discuta o movimento dos diversos valores de x. E um movimento
ligado ou n˜o ligado? Em um gr´fico, mostre onde est˜o os valores de equil´
a a a ıbrio. S˜o
a
eles est´veis ou inst´veis? Encontre o ponto de giro para E = −W/8, sabendo-se que
a a
W ´ uma constante positiva.
e
Solu¸˜o: Reescreva o potencial como
ca
U (x) −(y 2 + 1) x
Z(y) = = onde y = (2.107)
W y4 + 8 d
Primeiro, encontre os pontos de equil´
ıbrio, considerando o potencial.
dZ −2y 4y 3 (y 2 + 1)
= 4 + =0
dy y +8 (y 4 + 8)2
Isto ´ reduzido para
e
y(y 4 + 2y 2 − 8) = 0
y(y 2 + 4)(y 2 − 2) = 0
2
y0 = 2, 0
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

35. 2.6. ENERGIA --- 81
Assim
x01 = 0



√


x02 = 2d (2.108)

√ 

x03 = − 2d
Estes s˜o os trˆs pontos de equil´
a e ıbrio. Consideremos U (x)/W versus x/d na Figura 2-16.
FIGURA 2-16
O equil´
ıbrio ´ est´vel em x02 e x03 , mas inst´vel em x01 . O movimento ´ delimitado para todas
e a a e
energias E < 0. Por fim, determinamos todos os pontos de giro para energia E por coloca¸˜o ca
E = U (x).
W −W (y 2 + 1)
E=− = U (y) = (2.109)
8 y4 + 8
y 4 + 8 = 8y 2 + 8
y 4 = 8y 2
√
y = ±2 2, 0 (2.110)
√ √
Os pontos de giro obtidos para E = −W/8, s˜o x = −2 2d e +2 2d, assim com x = 0 – quando
a
o ponto de equil´
ıbrio ´ inst´vel.
e a
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

36. 82 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
2.7 MOVIMENTO DE FOGUETES
A dinˆmica Newtoniana elementar possui uma aplica¸˜o interessante no Movimento de Foguetes.
a ca
Examinaremos dois casos, (1) movimento de foguetes no espa¸o livre e (2) ascens˜o vertical de
c a
foguetes sob efeito da gravidade. O primeiro caso exige uma aplica¸˜o da conserva¸˜o do momento
ca ca
linear. O segundo, requer aplica¸˜es mais complexas da Segunda Lei de Newton.
co
Movimento de Foguetes no Espa¸o Livre
c
Aqui assumiremos que o foguete (espa¸onave) move-se sem influˆncia de for¸as externas. Escol-
c e c
hemos um sistema fechado no qual a Segunda Lei de Newton possa ser aplicada. No espa¸o livre
c
(espa¸o sideral) o movimento da espa¸onave depender´ totalmente de sua pr´pria energia. Ela se
c c a o
movimentar´ pela rea¸˜o ` massa ejetada com velocidade elevada, isto ´, para conservar o momento
a ca a e
linear, a espa¸onave dever´ se mover na dire¸˜o oposta. O diagrama do movimento da espa¸onave
c a ca c
´ mostrado na figura 2-17. Num tempo qualquer t, a massa total instantˆnea da espa¸onave ´ m
e a c e
e a velocidade instantˆnea ´ v em rela¸˜o ao sistema de referˆncia inercial.
a e ca e
FIGURA 2-17
Assumiremos que haver´ movimento apenas na dire¸˜o x, desta forma eliminaremos a nota¸˜o
a ca ca
vetorial. Durante o intervalo de tempo dt uma massa dm ser´ ejetada pelo sistema de propuls˜o
a a
do foguete com velocidade −u em rela¸˜o a espa¸onave. Imediatamente ap´s a massa dm ser
ca c o
ejetada, a massa da espa¸onave e sua velocidade ser˜o m − dm e v + dv, respectivamente.
c a
Momento inicial = mv (no tempo t) (2.111)
Momento final = (v − dm )(v + dv) + dm (v − u) (no tempo t + dt)
Espa¸onave sem dm
c Descarga do foguete dm (2.112)
Observe que a velocidade de eje¸˜o da massa dm em rela¸˜o ao sistema de referˆncia ´ v − u. A
ca ca e e
conserva¸˜o do momento linear exige que as Equa¸˜es 2.111 e 2.112 sejam iguais. N˜o h´ for¸as
ca co a a c
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

37. 2.7. MOVIMENTO DE FOGUETES --- 83
externas (Fext = 0).
pinicial = pfinal
p(t) = p(t + dt)
mv = (m − dm )(v + dv) + dm (v − u) (2.113)
mv = mv + mdv − vdm − dm dv + vdm − udm
mdv = udm
dm
dv = u (2.114)
m
Onde desprezamos o produto das duas diferenciais dm dv. Temos que considerar que dm seja uma
massa positiva ejetada da espa¸onave. A mudan¸a na massa da pr´pria espa¸onave ´ dm, onde
c c o c e
dm = −dm (2.115)
e
dm
dv = −u (2.116)
m
porque dm deve ser negativo. Assumindo m0 e v0 como sendo a massa e velocidade inicial da
espa¸onave, respectivamente, e integrando a Equa¸˜o 2.116 para os valores finais de m e v.
c ca
v m
dm
dv = −u
v0 m0 m
m0
v − v0 = u ln (2.117)
m
m0
v = v0 + u ln (2.118)
m
A velocidade de exaust˜o u ´ considerada constante. Assim, para maximizar a velocidade da
a e
espa¸onave, precisamos maximizar a velocidade de exaust˜o u e a raz˜o m0 /m.
c a a
Sendo que a velocidade final da espa¸onave ´ limitada pela raz˜o m0 , os engenheiros tiveram
c e a m
que construir foguetes com multi-est´gios. A massa m´
a ınima (sem combust´ ıvel) da espa¸onave ´
c e
limitada pela estrutura do material. Contudo, se o tanque de combust´ ıvel puder ser dispensado
ap´s a queima, a massa restante da espa¸onave ser´ menor. A espa¸onave poder´ conter dois ou
o c a c a
mais tanques de combust´ ıvel, podendo cada um deles ser descartados separadamente.
Por exemplo, seja
m0 = Massa total inicial da espa¸onave
c
m1 = ma + mb
ma = Massa do primeiro est´gio carregado
a
mb = Massa do primeiro est´gio (tanque de combust´
a ıvel, etc.)
v1 = Velocidade final do primeiro est´gio na combust˜o
a a
completa, ap´s todo combust´ ser queimado
o ıvel
m0
v1 = v0 + u ln (2.119)
m1
Ap´s a combust˜o completa a velocidade v1 do primeiro est´gio ´ alcan¸ada, e a massa mb ´
o a a e c e
descartada no espa¸o. A seguir, o foguete do segundo est´gio ´ acionado com a mesma velocidade
c a e
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

38. 84 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
de exaust˜o, e temos ent˜o
a a
ma = Massa total inicial da espa¸onave no segundo est´gio
c a
m2 = mc + md
mc = Massa do segundo est´gio carregado
a
md = Massa do segundo est´gio (tanque de combust´
a ıvel, etc.)
v1 = Velocidade inicial do segundo est´gio
a
v2 = Velocidade final do segundo est´gio ap´s combust˜o completa
a o a
ma
v2 = v1 + u ln (2.120)
m2
m0 ma
v2 = v0 + u ln (2.121)
m1 m2
O produto (m0 ma /m1 m2 ) pode ser muito maior que somente (m0 /m1 ). Foguetes com multi-
est´gios s˜o mais comumente usados na decolagem sob a a¸˜o da gravidade do que no espa¸o
a a ca c
livre.
Vimos que as espa¸onaves s˜o impulsionadas como resultado da conserva¸˜o do momento
c a ca
linear. Mas os engenheiros e cientistas preferem se referir ao termo for¸a atrav´s da express˜o
c e a
“propuls˜o” do foguete. Se multiplicarmos a Equa¸˜o 2.116 por m e dividirmos os dois lados por
a ca
dt ,temos
dv dm
m = −u (2.122)
dt dt
Como no lado esquerdo da equa¸˜o “aparece” ma(for¸a), o lado direito ´ chamado de propuls˜o:
ca c e a
dm
Propuls˜o ≡ −u
a (2.123)
dt
Como dm/dt ´ negativo, a propuls˜o ser´ positiva.
e a a
˜ ¸˜
ASCENSAO VERTICAL SOB A ACAO DA GRAVIDADE
O movimento real de um foguete tentando deixar o campo gravitacional da terra ´ muito compli-
e
cado. Para prop´sitos anal´
o ıticos, come¸amos fazendo v´rias simplifica¸˜es. O foguete ter´ somente
c a co a
movimento vertical, sem um componente horizontal. Desprezaremos a resistˆncia do ar e assumi-
e
remos que a acelera¸˜o da gravidade ´ constante com a altura. Tamb´m assumiremos que a taxa
ca e e
de queima de combust´ ıvel seja constante. Todos estes fatores que foram desprezados podem ser
inclu´ıdos em uma an´lise num´rica computacional.
a e
Podemos usar os resultados do caso anterior de movimento de foguete em um espa¸o livre,
c
por´m n˜o temos mais Fext = 0. A geometria est´ apresentada na Figura 2-18. Novamente temos
e a a
dm positiva, com dm = −dm . A for¸a externa Fext ´
c e
d
Fext = (mv)
dt
ou
Fext dt = d(mv) = dp = p(t + dt) − p(t) (2.124)
com respeito a um pequeno instante de tempo diferencial.
Para o sistema da nave espacial, encontramos as equa¸˜es do momento linear final e inicial
co
nas Equa¸˜es 2.111–2.116. Agora usamos estes resultados na equa¸˜o 2.116 para obter
co ca
P (t + dt) − p(t) = mdv + udm (2.125)
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

39. 2.7. MOVIMENTO DE FOGUETES --- 85
FIGURA 2-18
No espa¸o livre, Fext = 0, mas na ascens˜o, Fext = −mg. Combinando as Equa¸˜es 2.124 e 2.125
c a co
obtemos
Fext dt = − mg dt = m dv + u dm ⇒ −mg = mv + um
˙ ˙ (2.126)
Como a taxa de queima de combust´ ´ constante,
ıvel e
dm
m=
˙ = −α , α>0 (2.127)
dt
a Equa¸˜o 2.126 se torna
ca
α
dv = −g +
u dt (2.128)
m
Esta equa¸˜o, entretanto, tem trˆs vari´veis desconhecidas (v, m, t), portanto, usamos a Equa¸˜o 2.127
ca e a ca
para eliminar o tempo, obtendo
g u
dv = − dm (2.129)
α m
Assumindo que os valores inicial e final da velocidade sejam 0 e v, respectivamente e da massa m0
e m respectivamente, assim temos que
v m
g u
dv = − dm
0 m0 α m
g m0
v=− (m0 − m) + u ln (2.130)
α m
Podemos integrar a Equa¸˜o 2.127 para obter o tempo:
ca
m t
dm = −α dt
m0 0
m0 − m = αt (2.131)
A Equa¸˜o 2.130 se torna
ca
m0
v = −gt + u ln (2.132)
m
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

40. 86 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Podemos continuar com a Equa¸˜o 2.130 e integrar mais uma vez para determinar a altura
ca
do foguete (problema 2-52). Tal integra¸˜o ´ tediosa e o problema ´ facilmente manejado por
ca e e
m´todos computacionais. Mesmo com o fim da exaust˜o, o foguete continuar´ subindo porque
e a a
ainda possui velocidade vertical de subida. Eventualmente, com as simplifica¸˜es precedentes, a
co
for¸a gravitacional ir´ parar o foguete (porque assumimos a gravidade constante, sem diminuir
c a
com a altura).
Uma situa¸˜o interessante ocorre quando a velocidade de exaust˜o u n˜o ´ suficientemente
ca a a e
grande para fazer v na Equa¸˜o 2.132 ser positiva. Neste caso, o foguete permanecer´ no ch˜o.
ca a a
Esta situa¸˜o ocorre por causa dos limites de integra¸˜o que assumimos na Equa¸˜o 2.130. Dever´
ca ca ca ıa
ser necess´rio queimar combust´ suficiente antes que a propuls˜o do foguete o levantasse do ch˜o
a ıvel a a
´
(ver problema 2-54). E claro que foguetes n˜o s˜o projetados desta maneira; eles s˜o feitos para
a a a
alcan¸ar alturas desejadas a medida que os foguetes atingem taxa de queima m´xima.
c a
E X E M P L O 2.14 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
Considere o primeiro est´gio de um foguete Saturno V usado pelo programa lunar
a
Apollo. A massa inicial ´ de 2.8 × 106 kg, e a massa de combust´
e ıvel do primeiro
est´gio ´ de 2.1 × 106 kg. Assuma uma baixa propuls˜o de 37 × 106 N. A velocidade de
a e a
exaust˜o ´ de 2, 600m/s. Calcule a velocidade final do primeiro est´gio ap´s a com-
a e a o
bust˜o. Usando o resultado do Problema 2-52 (Equa¸˜o 2.133). Logo ap´s, calcule a
a ca o
altura de combust˜o.
a
Solu¸˜o: Para a propuls˜o (Equa¸˜o 2.123), determinamos o valor da combust˜o:
ca a ca a
dm P ropulsao 37 × 106 N
= = = −1.42 × 104 Kg/s
dt −u −2600m/s
A massa final do foguete ´ (2.8 × 106 kg − 2.1 × 106 kg) que ´ igual a 0.7 × 106 kg. Podemos usar a
e e
Equa¸˜o 2.130 para determinarmos a velocidade do foguete durante a combust˜o (vb ):
ca a
9.8m/s2 (2.1 × 106 kg) 2.8 × 106 kg
vb = − + 2600m/s ln
1.42 × 104 kg/s 0.7 × 106 kg
vb = 2.16 × 103 m/s
O momento da combust˜o tb , dado pela Equa¸˜o 2.131, ´
a ca e
m0 − m 2.1 × 106 kg
tb = = = 148s
α 1.42 × 104 kg/s
ou aproximadamente 2 1 min.
2
Usamos o resultado do Problema 2-52 para obtermos a altura da combust˜o yb :
a
1 mu m0
yb = utb − gt2 − ln (2.133)
2 b α m
1
yb = (2600m/s)(148s) − (9.8m/s2 ) · (148s)2
2
(0.7 × 106 kg) · (2600m/s) 2.8 × 106 kg
− 4 kg/s
ln
1.42 × 10 0.7 × 106 kg
yb = 9.98 × 104 m ≈ 100km
A altura real ser´ cerca de somente dois ter¸os deste valor.
a c
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

41. 2.7. MOVIMENTO DE FOGUETES --- 87
E X E M P L O 2.15 − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
O ˆnibus espacial tem sido descrito como uma incr´
o ıvel m´quina voando. Embora o
a
o
ˆnibus ´ tamb´m complexo para descrevermos completamente, podemos examinar
e e
a ascen¸˜o do lan¸amento fazendo algumas considera¸˜es. Dois sistemas prim´rios
ca c co a
levantam a nave do ch˜o para a ´rbita. O principal mecanismo do ˆnibus espa-
a o o
cial (SSME) constitui-se de trˆs outros mecanismos interiores a nave, queimando
e
hidrogˆnio l´
e ıquido (LH2 ) e oxigˆnio l´
e ıquido (LO2 ) armazenados em um grande tanque
preso a parte externa para a nave decolar. O principal impulso prov´m de dois fogue-
e
tes auxiliados por combust´ıveis s´lidos (SRB) presentes nos lados externos do tanque.
o
Ambos sistemas realizam a queima durante os dois primeiros minutos de lan¸amento,
c
depois que o combust´ ıvel no SRB ´ consumido as arma¸˜es SRB s˜o lan¸adas ao
e co a c
1
mar (Figura 2-19) para serem resgatadas depois no oceano. Durante os pr´ximos 6 2
o
minutos
FIGURA 2-19 Lan¸amento e ascen¸˜o do ˆnibus espacial, colocando a nave em ´rbita. O tempo est´ descrito entre
c ca o o a
parˆnteses ao lado do evento (minutos:segundos).
e
os SSMEs mantˆm o ˆnibus espacial em ascen¸˜o e fornecem a maior parte da velo-
e o ca
cidade horizontal necess´ria para entrar em ´rbita.
a o
Embora n˜o seja totalmente correto, assumimos que o foguete est´ se movendo
a a
verticalmente durante a queima do SRB (2 minutos) e calculamos a velocidade e altura
do ˆnibus. Tamb´m assumimos que durante os pr´ximos 6 1 minutos de vˆo o ˆnibus
o e o 2 o o
est´ se movendo 45◦ para a horizontal, e calculamos sua velocidade orbital.
a
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

42. 88 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
Os dados espec´
ıficos para as trˆs principais partes do ˆnibus espacial para uma
e o
ıpica altura s˜o∗
t´ a
Nave Espacial (atual spa¸onave/aeronave):
c
Massa com carga paga: 105, 000 Kg
Tanque Externo (combust´ para SSME):
ıvel
Tanque cheio: 36, 000 Kg
Combust´ıveis LH2 e LO2 : 7.2 × 105 Kg
Massa total carregada: 7.56 × 105 Kg
SRBs (dois):
Massa total quando vazio: 1.68 × 105 Kg
Combust´ S´lido: 1.01 × 106 Kg
ıvel o
Massa total carregada: 1.18 × 106 Kg
Massa total do ˆnibus espacial abastecido no lan¸amento: 2.04 × 106 Kg
o c
Propuls˜o de todos os SSMEs: 5.0 × 106 N
a
Propuls˜o de todos os SRBs: 23.6 × 106 N
a
Propuls˜o total no lan¸amento: 28.6 × 106 N
a c
Embora os SSMEs queimem em diferentes n´ ıveis de energia para manter a acelera¸˜o
ca
inferior a 3g (porque existem limita¸˜es na estrutura da nave, n˜o por causa dos
co a
astronautas), assumimos que os SSMEs queimam de maneira constande durante 8 1 2
minutos completos.
Solu¸˜o: Durante os 2 primeiros minutos, quando ambos sistemas mecˆnicos est˜o em aqueci-
ca a a
mento, n˜o ´ errado se adicionarmos o impulso para ambos sistemas, para encontrar a dm/dt total,
a e
e usar a Equa¸˜o 2.123 para encontrar uma velocidade m´dia de escapamento u.
ca e
Primeiros 120 segundos:
∆m(SRB) = 1.01 × 106 Kg
2
∆m(SSM E) = 7.2 × 105 Kg = 1.7 × 105 Kg
8.5
dm 1.18 × 106 Kg
=− = −9800Kg/s
dt 120s
Da Equa¸˜o 2.127, α = 9800Kg/s.
ca
a co ˆ
∗ Os dados s˜o de K. M. Joels, G. P. Kennedy, e D. Larkin, O Manual de Opera¸˜es do Onibus Espacial (New
York: Ballantine, 1982).
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

43. 2.7. MOVIMENTO DE FOGUETES --- 89
Impulso 28.6 × 106 N
u= = = 2900m/s
−dm/dt 9800Kg/s
m0 = 2.04 × 106 Kg
Combust´ carbonizado = 1.18 × 106 Kg
ıvel
m = 0.86 × 106 Kg
Calculamos a velocidade de carboniza¸˜o usando a Equa¸˜o 2.130:
ca ca
9.8m/s2 (1.18 × 106 Kg) 2.04
v= + (2900m/s) ln
9800Kg/s 0.86
v = 1325m/s ≈ 2900M P H
A altura pode ser determinada pela Equa¸˜o 2.133:
ca
1
v = 2900m/s(120s) − 9.8m/s2 (120s)2
2
(0.86 × 106 Kg) · (2900m/s) 2.04
− ln = 58Km ≈ 36miles
9800Kg/s 0.86
Os valores atuais na combust˜o comtleta do SRB est˜o em torno de v = 1300m/s e y = 45Km.
a a
Com o tempo as arma¸˜es SRB s˜o lan¸adas ao mar, o ˆnibus inicia o giro em torno de si
co a c o
preparando-se para entrar em ´rbita. Na dire¸˜o horizontal, o vˆo ocorre como se estivesse em
o ca o
um espa¸o livre (desprezando a resistencia do ar, a qual ´ pequena a uma altitude de 50Km). A
c e
propuls˜o dos SSMEs n˜o ´ suficiente para acelerar o ˆnibus verticalmente, mas mant´m o ˆnibus
a a e o e o
para este pousar suavemente. Vamos assumir que agora o ˆngulo de ascen¸˜o ´ em m´dia 45◦ e
a ca e e
usar a Equa¸˜o 2.118 para calcular a velocidade horizontal.
ca
m0 (ap´s lan¸ar as arma¸˜es SRB): 6.9 × 105 Kg
o c co
Combust´ localizado no tanque externo: 5.5 × 105 Kg
ıvel
m (ap´s interromper SSME): 1.4 × 105 Kg
o
Calculamos a velocidade de escapamento do SSME usando a Equa¸˜o 2.123:
ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

44. 90 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
impulso
u=−
dm/dt
dm 5.5 × 105 Kg
(SSM E) = − 60s = −1400Kg/s
dt 6.5min min
−5 × 106 N
u= = 3550m/s
−1400Kg/s
uhorz = 3550m/s(cos 45◦ ) = 2500m/s
6.9
uhorz = (2500m/s) ln
1.4
= 4000m/s ≈ 8900MPH
Ap´s esgotar todo o combust´ do tanque externo, os SSMEs desligam e o tanque externo
o ıvel
´ lan¸ado ao mar. O sistema que manobra a nave consiste de dois mecanismos propulsores de
e c
(27,000-N) , eventualmente colocando a nave na posi¸˜o correta da orbita com uma velocidade de
ca
aproximadamente 8,000 m/s e altitude de 400 Km.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
2.8 ¸˜ ˆ
LIMITACOES DA MECANICA NEWTONIANA
Neste cap´ ıtulo, introduzimos conceitos como posi¸˜o, tempo, momento e energia. Conclu´
ca ımos
que todas s˜o grandezas mensur´veis e que podem ser especificadas com alguma precis˜o desejada,
a a a
dependendo somente do grau de sofistica¸˜o dos instrumentos de medida. De certo, esta implica¸˜o
ca ca
aparenta ser verificada em nossas experiˆncias com todos os objetos macrosc´picos. Em qualquer
e o
instante do tempo, por exemplo, podemos medir com grande precis˜o a posi¸˜o de, por exemplo,
a ca
um planeta em ´rbita em torno do sol. Uma s´rie de tais medi¸˜es nos permite determinar (tamb´m
o e co e
com grande precis˜o) a velocidade do planeta em qualquer posi¸˜o.
a ca
Quando tentamos fazer medi¸˜es de objetos microsc´picos, entretanto, encontramos uma
co o
limita¸˜o fundamental na precis˜o dos resultados. Por exemplo, podemos (satisfatoriamente) medir
ca a
a posi¸˜o de um el´tron pelo espalhamento de um f´ton de luz pelo el´tron. O car´ter ondulat´rio
ca e o e a o
do f´ton impede uma medi¸˜o exata, e s´ podemos determinar a posi¸˜o do el´tron dentro de uma
o ca o ca e
incerteza ∆x relacionada com o tamanho (isto ´, comprimento de onda) do f´ton. Pelo pr´prio
e o o
ato de medi¸˜o, entretanto, induzimos uma mudan¸a de estado do el´tron, pois o espalhamento do
ca c e
f´ton transmite momento ao el´tron. Este momento possui uma incerteza ∆p. O produto ∆x ∆p
o e
´ uma medida da precis˜o com a qual podemos medir simultaneamente a posi¸˜o e o momento
e a ca
e relacionado a este, a velocidade; ∆x → 0, ∆p → 0 implica uma medi¸˜o com uma precis˜o
ca a
inimagin´vel. Foi mostrado pelo f´
a ısico alem˜o Werner Heisenlug (1901-1976) em 1927, que este
a
produto deve ser sempre maior que um certo valor m´ ınimo.∗ N˜o podemos ent˜o, especificar
a a
simultaneamente ambos posi¸˜o e momento do el´tron com uma precis˜o infinita, pois para ∆x →
ca e a
0, ent˜o ∆p → ∞ pelo Princ´
a ıpio da Incerteza de Heisenberg† poder ser satisfat´rio.
o
∗ Este resultado pode ser aplicado para medidas de energia num tempo particular, em cada caso o produto ´
e
certamente ∆E ∆t (Possuindo as mesmas dimens˜es ∆x ∆p).
o
† N.T.: muitos f´
ısicos preferem se referir a este princ´
ıpio como o Princ´
ıpio da Imprecis˜o.
a
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

45. ¸˜ ˆ
2.8. LIMITACOES DA MECANICA NEWTONIANA --- 91
O valor m´ ınimo de ∆x ∆p ´ da ordem de 10−34 J s. Isto ´ extremamente pequeno para
e ˙ e
padr˜es macrosc´picos, para objetos na escala-laborat´rio n˜o existe dificuldade pr´tica em fazer-
o o o a a
se medi¸˜es simultˆneas de posi¸˜o e momento. As leis de Newton podem portanto ser aplicadas
co a ca
se a posi¸˜o e o momento podem ser precisamente definidos. Mas pelo Princ´
ca ıpio da Incerteza,
a mecˆnica Newtoniana n˜o pode ser aplicada ` sistemas microsc´picos. Para solucionar estas
a a a o
dificuldades fundamentais no sistema newtoniano, um novo m´todo para tratar fenˆmenos mi-
e o
crosc´picos foi desenvolvido no in´
o ıcio de 1926. O trabalho de Ervin Schr¨dinger (1887-1961),
o
Heisenlug, Max Born(1872-1970), Paul Dirac (1902-1984) e outros subseq¨entemente colocaram u
esta nova disciplina sobre uma firme fundamenta¸˜o. A mecˆnica Newtoniana, ent˜o, ´ perfeit-
ca a a e
amente adequada para descrever fenˆmenos em larga escala. Por´m, precisamos da nova mecˆnica
o e a
(mecˆnica quˆntica) para analisar processos no dom´
a a ınio atˆmico. Quanto mais o tamanho do
o
sistema aumenta de escala, a mecˆnica quˆntica tende ` mecˆnica newtoniana.
a a a a
Em adi¸˜o as limita¸˜es fundamentais da mecˆnica Newtoniana, como na aplica¸˜o a objetos
ca co a ca
microsc´picos, existe uma dificuldade inerente no esquema Newtoniano – o que reside no conceito
o
de tempo. Na vis˜o Newtoniana, o tempo ´ absoluto, isto ´, sup˜e-se que seja sempre poss´
a e e o ıvel
determinar sem ambig¨idade quando dois eventos ocorreram simultaneamente ou quando um pre-
u
cedeu o outro. Para decidir a seq¨ˆncia temporal de eventos, os dois observadores devem estar
ue
em comunica¸˜o instantˆnea, atrav´s de algum tipo de sinal ou estabelecendo-se dois rel´gios em
ca a e o
sincronismo exato em seus pontos de observa¸˜o. Por´m, a sincroniza¸˜o dos rel´gios para ser
ca e ca o
exata requer o conhecimento do tempo de trˆnsito de um sinal na dire¸˜o de um observador para
a ca
o outro (podemos conseguir isto dispondo de dois rel´gios sincronizados, mas isto ´ um argumento
o e
circular). Quando realmente medimos a velocidade dos sinais, entretanto, sempre obtemos uma
velocidade m´dia de propaga¸˜o em dire¸˜es opostas. E para criar um experimento que me¸a a
e ca co c
velocidade somente em uma dire¸˜o de propaga¸˜o inevitavelmente nos leva a introdu¸˜o de novas
ca ca ca
generaliza¸˜es que n˜o podemos determinar antes do experimento.
co a
Sabemos que comunica¸˜o instantˆnea por sinaliza¸˜o ´ imposs´
ca a ca e ıvel: intera¸˜es entre corpos
co
materiais propagam-se com uma velocidade finita, e uma intera¸˜o de algum tipo deve ocorrer
ca
para que um sinal seja transmitido. A velocidade m´xima de propaga¸˜o de qualquer sinal ´ a
a ca e
velocidade da luz no espa¸o livre(v´cuo): c ∼ 3 × 108 m/s.∗
c a =
As dificuldades em estabelecer-se uma escala de tempo entre corpos separados nos leva acre-
ditar que o tempo, afinal de contas, n˜o ´ absoluto, e que o tempo e o espa¸o est˜o de alguma
a e c a
maneira intimamente relacionados. A solu¸˜o para este dilema foi encontrada no per´
ca ıodo de 1904-
1905 por Hendrik Lorenz (1853-1928), Henri Poincar´ (1854-1912) e Albert Einstein (1879-1955)
e
e foi resumido na teoria especial da relatividade (ver Cap´ ıtulo 14).
A mecˆnica Newtoniana est´, portanto, sujeita a limita¸˜es fundamentais quando pequenas
a a co
distˆncias ou grandes velocidades s˜o encontradas. Dificuldades com a mecˆnica Newtoniana
a a a
tamb´m podem ocorrer quando objetos extremamente massivos ou enormes distˆncias est˜o en-
e a a
volvidas. Uma limita¸˜o pr´tica tamb´m ocorre quando o sistema ´ constitu´ por um grande
ca a e e ıdo
n´mero de corpos. No Cap´
u ıtulo 8, veremos que podemos obter uma solu¸˜o geral de maneira ca
concisa para o movimento de um sistema constitu´ de mais de dois corpos em intera¸˜o mesmo
ıdo ca
que esta seja simplesmente gravitacional. Para calcular o movimento num sistema, de trˆs cor- e
pos, devemos recorrer a procedimentos de aproxima¸˜o num´rica. Embora tal m´todo seja, em
ca e e
princ´ıpio, capaz de qualquer exatid˜o desejada, o trabalho envolvido ´ consider´vel. O movimento
a e a
de sistemas ainda mais complexos (por exemplo, o sistema composto de todos grandes objetos no
sistema solar) pode, da mesma maneira, ser computado, mas o procedimento se torna rapidamente
muito pesado para ser utilizado para qualquer sistema grande. Para calcular o movimento de
mol´culas individuais em, digamos, um cent´
e ımetro c´bico de g´s contendo ≈ 101 9 mol´culas ´ cla-
u a e e
ramente imposs´ ıvel. Um m´todo bem sucedido de calcular as propriedades m´dias de tais sistemas
e e
foi desenvolvido na segunda metade do s´culo dezenove por Boltzman, Maxwell, Gibbs, Liouville
e
∗ A velocidade da luz ´ bem definida como 299, 792, 458.0 m/s fazendo compara¸˜es com outras medidas mais
e co
padronizadas. Metro ´ a defini¸˜o de diatˆncia viajada pela luz no v´cuo durante um intervalo de tempo de
e ca a a
1/299, 792, 458 de um segundo.
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

46. 92 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
e outros. Estes procedimento permitiram a dinˆmica dos sistemas serem calculados atrav´s da
a e
teoria de probabilidades, e uma mecˆnica estat´
a ıstica foi desenvolvida. Alguns coment´rios sobre a
a
formula¸˜o de conceitos estat´
ca ıstico em mecˆnica podem ser encontrados na Se¸˜o 7.13.
a ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

47. ¸˜ ˆ
2.8. LIMITACOES DA MECANICA NEWTONIANA --- 93
PROBLEMAS
2-2. Uma part´ıcula de massa m ´ for¸ada a mover-se na superf´ de uma esfera de raio R por
e c ıcie
uma for¸a aplicada F(θ, φ). Escreva a equa¸˜o do movimento.
c ca
2-5. Um piloto de um jato de guerra percebe que ´ capaz de suportar uma acelera¸˜o de 9g antes
e ca
de ser jogado para fora. O piloto aponta para baixo no plano vertical dele at´ mover-se a
e
uma velocidade de Mach 3 e pretende virar-se para cima em uma manobra circular antes de
colidir contra o solo. (a) Onde ocorre a acelera¸˜o m´xima na manobra? (b) Qual o c´
ca a ırculo
m´ınimo que o piloto pode empregar?
2-6. Na nevasca de 88, uma vaqueira foi for¸ada a soltar fardos de feno de um aeroplano para
c
alimentar sua cria¸˜o de gado. O aeroplano voou horizontalmente a 160 Km/h e abandonou
ca
os fardos a uma altura de 80 m sobre o plano alcan¸ado. (a) Ela procura os fardos aterrizados
c
sobre a forragem 30 m atr´s do gado de modo que n˜o chega a encontr´-los. Onde ela deveria
a a a
soltar os fardos do aeroplano? (b) Para n˜o encontrar o gado, qual ´ o grande erro de tempo
a e
que ela cometeu ao empurrar os fardos para fora do aeroplano? Despreze a resistˆncia do ar.
e
2-7. Inclua a resistˆncia do ar para os fardos de feno no problema anterior. Um fardo de feno
e
tem aproximadamente 30 Kg e uma ´rea m´dia de aproximadamente 0.2m2 . Considere a
a e
resistˆncia como sendo proporcional ao quadrado da velocidade e considere cW = 0.8. Esbo¸e
e c
as trajet´rias com um computador se os fardos de feno aterrizam 30m atr´s do gado para
o a
ambas situa¸˜es, ou seja, com e sem resistˆncia do ar. Se os fardos de feno foram liberados ao
co e
mesmo tempo nos dois casos, qual ´ a distˆncia entre as posi¸˜es de aterrizagem dos fardos?
e a co
2-10. Repita o Exemplo 2.4 executado por uma calculadora usando um computador para resolver
a Equa¸˜o 2.22. Use os seguintes valores: m = 1Kg, v0 = 10m/s, x0 = 0, e k = 0.1s−1 .
ca
Esbo¸e os planos de v versus t, x versus t, e v versus x. Compare com os resultados do
c
Exemplo 2.4 para ver se seus resultados s˜o razo´veis.
a a
2-11. Considere uma part´ ıcula de massa m que se mant´m do in´ at´ o fim do movimento em
e ıcio e
um campo gravitacional constante. Se uma for¸a de resistˆncia proporcional ao quadrado da
c e
velocidade (isto ´, kmv 2 ) ´ encontrada, mostre que a distˆncia s da queda da part´
e e a ıcula em
acelera¸˜o de v0 para v1 ´ dada por
ca e
2
1 g − kv0
s(v0 → v1 ) = ln 2
2k g − kv1
2-12. Uma part´ ıcula est´ projetada verticalmente para cima em um campo gravitacional constante
a
com uma velocidade inicial v0 . Mostre que se h´ uma for¸a de retardamento proporcional
a c
ao quadrado da velocidade instantˆnea, a velocidade da part´
a ıcula quando ela retorna a sua
posi¸˜o inicial ´
ca e
v0 vt
2 2
v0 + vt
onde vt ´ a velocidade final(terminal).
e
2-13. Uma part´ ıcula move-se sob a influˆncia de uma for¸a de retardamento equivalente a mk(v 3 +
e c
a2 v), onde k e a s˜o constantes. Mostre que para alguns valores de velocidade inicial a
a
part´ıcula nunca ir´ se mover a uma distˆncia maior do que π/2ka e que a part´
a a ıcula cessa o
movimento somente para t → ∞.
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

48. 94 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
2-15. Uma part´ıcula de massa m escorrega para baixo em um plano inclinado sob influˆncia da
e
gravidade. Se o movimento ´ contido por uma for¸a f = kmv 2 , mostre que o tempo requerido
e c
para a part´
ıcula mover-se a uma distˆncia desde o in´ at´ cessar o movimento ´
a ıcio e e
cosh−1 (ekd )
t= √
kg sin θ
onde θ ´ o ˆngulo de inclina¸˜o do plano.
e a ca
2-17. Um forte jogador bate na bola elevando-a a uma altura de 0.7 m acima de uma casa. Todas
as batidas dos jogadores possuem um ˆngulo de eleva¸˜o de 350 e movem-se em dire¸˜o a
a ca ca
um muro de 2 m de altura e 60 m distante do centro do campo. Qual a velocidade inicial
necess´ria para a bola deixar o centro do campo ao muro? Ignore a resistˆncia do ar.
a e
2-18. Inclua a resistˆncia do ar proporcional ao quadrado da velocidade da bola no problema
e
precedente. Considere o coeficiente de resistˆncia cw = 0.5, o raio da bola como 5 cm e uma
e
massa de 200 g. (a) Encontre a velocidade inicial da bola necess´ria para alcan¸ar o muro.
a c
(b) Para esta velocidade, encontre o ˆngulo de eleva¸˜o inicial que permite ` bola facilmente
a ca a
alcan¸ar o muro. Agora a bola pode verticalmente alcan¸ar o muro?
c c
2-19. Se um proj´til move-se tal que a distˆncia do ponto de proje¸˜o ´ sempre crescente, encontre
e a ca e
o ˆngulo horizontal m´ximo com que a part´
a a ıcula pode ter sido projetada. (Assuma que n˜oa
existe resistˆncia do ar)
e
2-20. Um estintor de incˆndio projeta seu jato em um corpo de massa 10kg, do tipo a que as
e
curvas de Figura 2-3 se aplicam. A velocidade do jato ´ 140m/s. Com que ˆngulo deve estar
e a
o tambor elevado para bater em um alvo no mesmo plano horizontal que o extintor e 100m
distante? Compare os resultados com aqueles para o exemplo sem retardamento.
2-22. O movimento de uma part´ ıcula carregada em um campo eletromagn´tico pode ser obtido
e
pela Equa¸˜o de Lorentz ∗ para a for¸a em uma part´
ca c ıcula em tal campo. Se o vetor do
campo el´trico for E e o vetor do campo magn´tico for B, a for¸a em uma part´
e e c ıcula de massa
m carrega com uma carga q que tem uma velocidade v ´ dada por
e
F = qE + qv×B
onde assumimos que v << c(velocidade da luz).
(a) Se n˜o houver nenhum campo el´trico e se a part´
a e ıcula entra num campo magn´tico em
e
sentido perpendicular `s linhas do fluxomagn´tico, mostre que a trajet´ria ´ um c´
a e o e ırculo
com raio
mv v
r= =
qB ωc
onde ωc ≡ qB/m ´ a frequˆncia do ciclotron.
e e
(b) Escolha a posi¸˜o do eixo z no sentido de B e deixe o plano E e B contido no plano xy.
ca
Assim
B = Bk, E = Ey j + Ez k
mostre que as componentes do movimento para z s˜o
a
qEz 2
z(t) = z0 + z0 t +
˙ t
2m
onde
z(0) ≡ z0 e z(0) ≡ z0
˙ ˙
∗ Veja, por exemplo, Heald e Marion, Radia¸˜o Eletromagn´tica Cl´ssica (95, Se¸˜o 1.7).
ca e a ca
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

49. ¸˜ ˆ
2.8. LIMITACOES DA MECANICA NEWTONIANA --- 95
(c) Continue o c´lculo e obtenha as expre¸˜es para x(t) e y(t). Mostre que as m´dias do
a co ˙ ˙ e
tempo destes componentes da velocidade s˜o
a
Ey
x =
˙ , y =0
˙
B
(Mostre que o movimento ´ peri´dico e ent˜o a m´dia sobre um per´
e o a e ıodo completo)
(d) Integre as equa¸˜es da velociade encontradas em (c) e mostre (com as condi¸˜es iniciais
co co
x(0) = −A/ωc , x(0) = Ey /B, y(0) = 0, y(0) = A) que
˙ ˙
−A Ey A
x(t) = cos ωc t + t, y(t) = sin ωc t
ωc B ωc
Estas s˜o as equa¸˜es param´tricas de um cicl´ide. Esboce a proje¸˜o da trajet´ria
a co e o ca o
no plano xy para os casos (i) A > |Ey /B|, (ii) A < |Ey /B|, e (iii) A = |Ey /B|. (O
ultimo caso da um cicl´ide.)
´ o
2-27. Uma corda que possui uma massa total de 0.4kg e comprimento total de 4m tem 0.6m de
corda suspensa verticalmente para baixo. Quanto trabalho deve ser feito para situar a corda
na bancada?
2-28. Uma superbola de massa M e uma bola de gude de massa m s˜o lan¸adas de uma altura h
a c
com a bola de gude exatamente no topo da superbola. Uma superbola tem um coeficiente
de restitui¸˜o perto de 1(i.e., sua colis˜o ´ essencialmente el´stica). Ignore o tamanho da
ca a e a
superbola e da bola de gude. A superbola colide com o solo, rebate e bate na bola de gude,
a qual move-se novamente para cima. Considerando que o movimento oferece resistˆncia, e
explique a eleva¸˜o do movimento e qual a eleva¸˜o da grande bola.
ca ca
2-29. Um autom´vel trafegando em uma estrada com grau de inclina¸˜o de 8%, colide fortemente
o ca
e derrapa 30m antes de parar totalmente. Um perito mediu o coeficiente de fric¸˜o cin´tico
ca e
entre os pneus e a estrada como sendo igual a µk = 0.45. O perito est´ correto em afirmar
a
que o motorista excedeu o limite de velocidade em 25 MPH? Explique.
2-30. Um estudante solta um bal˜o cheio d’´gua do telhado de uma alto edif´ urbano tentando
a a ıcio
atingir seu companheiro de quarto no solo (que est´ apressado). O primeiro estudante baixa
a
a cabe¸a para tr´s ouvindo distante o barulho da ´gua 4.021 s ap´s a queda do bal˜o. Se a
c a a o a
velocidade do som ´ 331 m/s, encontre a altura do edif´
e ıcio, desprezando a resistˆncia do ar.
e
2-31. No Exemplo 2.10, a velocidade inicial de aproxima¸˜o da particula carregada n˜o possui
ca a
componente ao longo do eixo x. Mostre que, mesmo que ela possuisse um componente x,
o movimento subsequente da part´ıcula seria o mesmo – que somente o raio da h´lice seria
e
alterado.
2-33. Execute um c´lculo de computador para um objeto que move-se verticalmente no ar sob
a
a gravidade e que experimenta uma for¸a de retardamento proporcional ao quadrado da
c
velocidade do objeto (veja a Equa¸˜o 2.21). Use as vari´veis m para a massa e r para
ca a
o raio do objeto. Todos os objetos s˜o deixados cair do repouso do alto de um edif´
a ıcio
100 − m − tall. Use um valor de cw = 0.5 e trace um plano no computador da altura y,
velocidade v, e acelera¸˜o a contra t para as seguintes condi¸˜es e responda `s perguntas:
ca co a
(a) Uma bola beisebol de m = 0.145 Kg e r = 0.0366 m.
(b) Uma bola de ping-pong de m = 0.0024 Kg e r = 0.0019 m.
(c) Um pingo de chuva de r = 0.003 m.
(d) Todos os objetos alcan¸am suas velocidades terminais? Discuta os valores das velocida-
c
des terminais e explique suas diferen¸as.
c
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

50. 96 --- 2 / MECANICA NEWTONIANA – PART´
ˆ ´
ICULA UNICA
(e) Como pode uma bola de beisebol ser jogada mais distante do que uma esfera do ping-
pong mesmo que a bola de beisebol seja muito mais maci¸a?
c
(f ) Discuta as velocidades terminais de pingos de chuva grandes e pequenos. Qual as
velocidades terminais dos pingos de chuva com raios 0.002 m e 0.004 m?
2-35. Execute os c´lculos num´ricos do Exemplo 2.7 para os valores dados na Figura 2-8. Trace
a e
ambas as Figuras 2-8 e 2-9. N˜o duplique a solu¸˜o no apˆndice H; componha sua pr´pria
a ca e o
solu¸˜o.
ca
2-36. A arma est´ localizada em uma ribanceira de altura h com vista para o vale do rio. Se a
a
velocidade do m´ ´ v0 , encontre a express˜o para o alcance como uma fun¸˜o da eleva¸˜o do
ıssil e a ca ca
a
ˆngulo da arma. Achar numericamente o m´ximo alcance fora do vale para uma determinada
a
h e v0 .
2-40. Uma part´
ıcula movimenta-se numa ´rbita bi-dimensional definida por:
o
x(t) = A(2αt − sin αt)
y(t) = A(1 − cos αt)
(a)Encontre a acelera¸˜o tangencial at e a acelera¸˜o normal an como uma fun¸˜o de tempo
ca ca ca
onde as componentes tangenciais e normal s˜o dadas em rela¸˜o a velocidade.
a ca
(b)Determine em quais momentos an tem um m´ximo na orbita.
a ´
2-41. Um trem move-se ao longo de uma trilha com uma velocidade constante u. Uma mulher no
trem joga uma bola de massa m para frente com uma velocidade v com respeito a si mesma.
(a) Qual ´ a energia cin´tica ganha pela bola em rela¸˜o a medida por uma pessoa no trem?
e e ca
(b) para uma pessoa de p´ sobre a via f´rrea? (c) Qual o trabalho feito pela mulher para
e e
jogar a bola e (d) do trem?
2-42. Um cubo s´lido de densidade uniforme e lado b est´ em equil´
o a ıbrio no topo do cilindro de
raio R (Figura 2-C). Os planos dos quatro lados do cubo s˜o paralelos ao eixo do cilindro.
a
O contato entre o cubo e a esfera ´ perfeitamente ´spero. Sob quais condi¸˜es o equil´
e a co ıbrio ´
e
est´vel ou n˜o?
a a
2-44. Resolva o Exemplo 2.12 usando de preferˆncia for¸as no lugar de energias. Como vocˆ pode
e c e
determinar se o sistema encontra-se em equil´
ıbrio inst´vel ou est´vel?
a a
ıbrio ´ est´vel ou inst´vel quando (d2 U/dx2 )0 = 0.
2-45. Descreva como se determina se um equil´ e a a
2-49. Um foguete extremamente bem-constru´ tem uma massa (m0 /m) de 10, um novo com-
ıdo
bust´ ´ desenvolvido tendo como velocidade da exaust˜o 4, 500m/s. A uma taxa constante
ıvel e a
para 300s. Calcule a velocidade m´xima deste foguete de est´gio unico, com acelera¸˜o con-
a a ´ ca
stante presumido da gravidade. Se a velocidade do escape de uma part´ ıcula da terra for
11.3km/s, pode um foguete de est´gio unico similar com a mesma raz˜o de massa e veloci-
a ´ a
dade de exaust˜o ser constru´ para alcan¸ar a lua?
a ıdo c
2-50. Uma gota da ´gua que cai na atmosfera ´ esf´rica. Suponha que como a gota passa atrav´s de
a e e e
uma nuvem, adquire massa a uma taxa proporcional a kA onde k ´ uma constante (> 0) e A
e
sua ´rea de se¸˜o transversal. Considere uma gota de raio inicial r0 que entra em uma nuvem
a ca
com velocidade v0 . Assuma que n˜o h´ for¸as resistivas e mostre (a) que o raio aumenta
a a c
linear com o tempo, e (b) que se o r0 for pequeno podendo ser desprez´ ent˜o a velocidade
ıvel a
aumenta linearmente com o tempo dentro da nuvem.
2-51. Um foguete num espa¸o distante de campo gravitacional desprez´
c ıvel come¸a do repouso a
c
acelerar uniformemente at´ uma velocidade v. A massa inicial do foguete ´ m0 . Quanto
e e
trabalho faz o motor do foguete?
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)

51. ¸˜ ˆ
2.8. LIMITACOES DA MECANICA NEWTONIANA --- 97
2-52. Considere um foguete de est´gio unico que faz exame fora da ´rbita da terra em que a altura
a ´ o
do foguete na queima total de combust´ ıvel est´ dada pela Equa¸˜o 2.133. Quanto mais
a ca
distante na altura ir´ o foguete ap´s a queima total do combust´
a o ıvel?
2-53. Um foguete tem uma massa inicial m e uma taxa de combust˜o do combust´ α(Equa¸˜o
a ıvel ca
2.127). Qual ´ a velocidade m´
e ınima da exaust˜o que permita que o foguete levante imedia-
a
tamente depois do acendimento?
2-54. Um foguete possui uma massa inicial de 7 × 104 Kg e no disparo queima-se combust´ na
ıvel
taxa de 250Kg/s. A velocidade de escape ´ 2.500m/s. Se o foguete tem uma subida vertical
e
partindo da Terra, quanto tempo depois do disparo do motor do foguete ser´ a decolagem
a
do foguete? O que est´ errado com o projeto deste foguete?
a
2-55. Considere um foguete de n est´gios, com cada velocidade de descarga u. Cada est´gio do
a a
foguete tem a mesma propor¸˜o de consumo (k = mi /mf ). Mostre que a velocidade final do
ca
est´gio nth ´ nu ln k.
a e
2-56. Para realizar um salvamento, uma embarca¸˜o lunar precisa pairar exatamente acima da
ca
superf´ da lua, a qual tem uma acelera¸˜o gravitacional de g/6. A velocidade de exaust˜o
ıcie ca a
´ 2, 000m/s, mas a quantidade de combust´ a ser usado ´ provavelmente apenas 20% da
e ıvel e
massa total. Por quanto tempo pode a embarca¸˜o pairar?
ca
2-57. Um novo lan¸a proj´til ´ desenvolvido no ano de 2013 que pode lan¸ar uma sonda esf´rica de
c e e c e
104 kg com velocidade inicial de 6, 000m/s. Para prop´sitos de testes, objetos s˜o lan¸ados
o a c
verticalmente.
(a) Desconsiderando a resistˆncia do ar e assumindo a acelera¸˜o da gravidade constante.
e ca
Determine a altura que o objeto lan¸ado pode alcan¸ar acima da superf´ da terra.
c c ıcie
(b) Se o objeto tem raio de 20cm e a resistˆncia do ar ´ proporcional ao quadrado da
e e
velocidade do objeto com Cw = 0.2. Determine a altura m´xima alcan¸ada, assumindo
a c
que a densidade do ar ´ constante.
e
(c) Agora tamb´m inclua o fato que a acelera¸˜o da gravidade decresce quando o objeto
e ca
sobe acima da terra. Encontre a altura alcan¸ada.
c
(d) Agora considere os efeitos do decr´scimo da densidade do ar com a altitude no c´lculo.
e a
Podemos muito grosseiramente representar a densidade do ar por log10 (ρ) = −0.05h +
0.11 onde ρ ´ a densidade em kg/m3 e h ´ a altitude acima da terra em km. Determine
e e
que altura o objeto vai alcan¸ar.
c
2-58. Um novo foguete com simples-est´gio ser´ desenvolvido em 2013, e ter´ uma velocidade de
a a a
exaust˜o de g´s de 4, 000m/s. A massa total do foguete ´ de 105 kg, com 90% dessa massa
a a e
sendo combust´ıvel. O combust´ queima rapidamente em 100s a uma taxa constante. Para
ıvel
propor um teste, o foguete ´ lan¸ado verticalmente a partir da superf´ da Terra. Dentro
e c ıcie
disso responda as partes (a) e (d) do problema anterior.
Projeto AIUTA – Mecˆnica Cl´ssica I
a a (UNIFRA–2004)