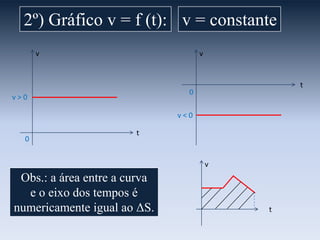
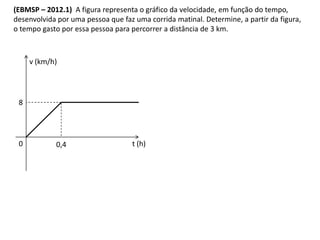
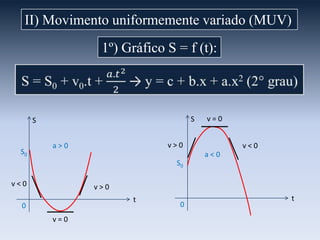
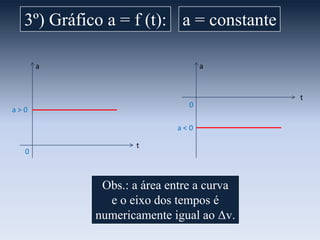
O documento apresenta os gráficos de cinemática para movimento uniforme e uniformemente variado. Para movimento uniforme, o gráfico da posição é uma reta e o da velocidade é uma linha horizontal. Para movimento uniformemente variado, os gráficos da posição e velocidade são parábolas e o da aceleração é uma linha reta, sendo a concavidade determinada pelo sinal da aceleração.

1. Gráficos de Cinemática
I) Movimento uniforme (MU)
1º) Gráfico S = f (t):
S = S0 + v.t → y = b + a.x (1 grau)
S
S0 = b (coef. linear)
v = a (coef. angular)
v>0
S0
0
t

2. 2º) Gráfico v = f (t): v = constante
v
v
t
0
v>0
v<0
0
t
v
Obs.: a área entre a curva
e o eixo dos tempos é
numericamente igual ao ΔS.
t

3. (EBMSP – 2012.1) A figura representa o gráfico da velocidade, em função do tempo,
desenvolvida por uma pessoa que faz uma corrida matinal. Determine, a partir da figura,
o tempo gasto por essa pessoa para percorrer a distância de 3 km.
v (km/h)
8
0
0,4
t (h)

4. II) Movimento uniformemente variado (MUV)
1º) Gráfico S = f (t):
S
S
S0
v=0
v>0
a>0
v<0
a<0
S0
v<0
v>0
t
0
v=0
0
t

5. Observações:
I) A concavidade é dada pelo sinal da aceleração.
II) As tangentes em cada ponto da curva representam
as velocidades instantâneas.
III) No instante correspondente ao vértice, o móvel
parou e vai inverter o sentido de movimento.
IV) Quando a curva cruza o eixo dos tempos (raízes
da equação), o móvel passa pela origem (S = 0).

6. 2º) Gráfico v = f (t):
v = v0 + a.t → y = B + A.x (1 grau)
v0 = B (coef. linear)
a = A (coef. angular)
v
a>0
Obs.: a área entre a curva
e o eixo dos tempos é
numericamente igual ao ΔS.
v0
0
t

7. 3º) Gráfico a = f (t): a = constante
a
a
0
a>0
a<0
0
t
Obs.: a área entre a curva
e o eixo dos tempos é
numericamente igual ao Δv.
t