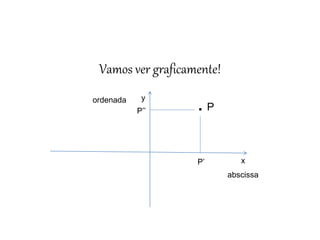
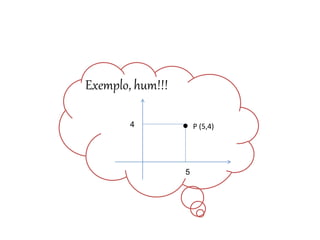
O documento discute equações de retas no sistema cartesiano, incluindo a equação geral da reta Ax + By + C = 0 e a equação reduzida da reta na forma Y = mX + b. Explica como calcular a distância entre dois pontos e derivar as equações de uma reta a partir de dois pontos nela.