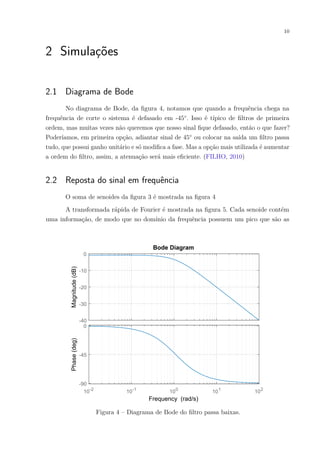
Este relatório descreve o projeto e simulação de um filtro passa baixas de primeira ordem usando um resistor e capacitor. Ele encontra a função de transferência do filtro, traça o diagrama de Bode, e simula a resposta do filtro a um sinal de entrada variando em frequência.

1. Halisson Tedesco
Filtro passa baixas de primeira ordem passivo
com resistor de carga.
Brasil
2016, Novembro

2. Halisson Tedesco
Filtro passa baixas de primeira ordem passivo com
resistor de carga.
Trabalho sobre filtro passa baixas referente
a disciplina de circuitos elétricos da universi-
dade federal de santa maria .
Universidade Federal de Santa Maria
Brasil
2016, Novembro

3. Lista de ilustrações
Figura 1 – Esquema elétrico do filtro feito no Psim. . . . . . . . . . . . . . . . . . 6
Figura 2 – Script par obter o digrama de Bode. . . . . . . . . . . . . . . . . . . . 7
Figura 3 – Soma de senoides para obter uma onda quadrada. . . . . . . . . . . . . 8
Figura 4 – Diagrama de Bode do filtro passa baixas. . . . . . . . . . . . . . . . . . 10
Figura 5 – Soma de senoides graficamente no Psim. . . . . . . . . . . . . . . . . . 11
Figura 6 – Resposta do sinal em frequência. . . . . . . . . . . . . . . . . . . . . . 11
Figura 7 – Comparação do sinal normal com o filtrado para 3k Hz. . . . . . . . . . 12
Figura 8 – Comparação sinal normal com o filtrado para 5k Hz. . . . . . . . . . . 12

4. Sumário
Objetivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
I DESCRIÇÃO DO RELATÓRIO 5
1 FILTROS PASSA BAIXAS COM RESISTOR DE CARGA . . . . . . 6
1.1 Função de Transferência . . . . . . . . . . . . . . . . . . . . . . . . . . 6
II RESULTADOS 9
2 SIMULAÇÕES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1 Diagrama de Bode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.2 Reposta do sinal em frequência . . . . . . . . . . . . . . . . . . . . . 10
2.2.1 Sinal Filtrado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3 CONCLUSÃO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
REFERÊNCIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

5. 4
Objetivo
O objetivo deste relatório é encontrar a função transferência de um filtro passa
baixas de primeira ordem, traçar o diagrama de Bode e ver a resposta a um sinal aplicado
em frequência.

6. Parte I
Descrição do relatório

7. 6
1 Filtros passa baixas com resistor de carga
1.1 Função de Transferência
A Figura 1 ilustra o esquema elétrico do filtro passa baixas. Podemos facilmente
encontrar o função de transferência por uma análise nodal no nó 1.
V0
RL
+
V0
1
sC
+
VO − Vi
R
= 0
VO
RL
+ V0sC +
V0 − Vi
R
= 0
V0R + V0sCRRL + RLV0 − RLVi = 0
V0(R + sCRRL + RL) = RLVi
logo,
H(s) =
V0
Vi
=
RL
sCRRL + R + RL
H(s) =
1
CR
s + R+RL
RRLC
Figura 1 – Esquema elétrico do filtro feito no Psim.

8. Capítulo 1. Filtros passa baixas com resistor de carga 7
Figura 2 – Script par obter o digrama de Bode.
que é a função de transferência do sistema da figura 1.
Através do MATLAB, podemos traçar o diagrama de Bode neste sistema com o
script da figura 2. Neste caso utilizamos um resistor em série (R) de 100 Ω, um resistor
em paralelo de carga (RL) de 1000 Ω e um capacitor de 10 mF. substituindo os valores
na função de transferência obtemos:
H(s) =
1
s + 1.1
que tem como polo s = −1.1 indicando que o sistema é estável, como era de se
esperar. O módulo do polo multiplicado por 2π nos dá a frequência de corte do filtro (6,911
rad/s), cujo ganho cai 3dB e o sistema fica atrasado em 45◦
. (OGATA, 2010)
Poderíamos querer obter o espectro de frequência de um sinal, por exemplo, senoidal.

9. Capítulo 1. Filtros passa baixas com resistor de carga 8
Figura 3 – Soma de senoides para obter uma onda quadrada.
Sabemos que uma onda quadrada1
pode ser representada por uma soma infinita de senos
e cossenos ponderados, dados pela Série de Fourier. Pode-se pegar uma função de uma
onda quadrada montar a serie de Fourier, encontrando:
g(t) =
4
π
∞
n=1
1
n
sen(nt)
para todo n ímpar.
Não podemos fazer uma soma infinita, mas podemos somar algumas senoides como
mostrado no figura 3. Em que H(s) é a função de transferência do nosso filtro.
1
NA verdade, qualquer sinal periódico contínuo pode ser representado por uma soma infinita de senos e
cossenos.

10. Parte II
Resultados

11. 10
2 Simulações
2.1 Diagrama de Bode
No diagrama de Bode, da figura 4, notamos que quando a frequência chega na
frequência de corte o sistema é defasado em -45◦
. Isso é típico de filtros de primeira
ordem, mas muitas vezes não queremos que nosso sinal fique defasado, então o que fazer?
Poderíamos, em primeira opção, adiantar sinal de 45◦
ou colocar na saída um filtro passa
tudo, que possui ganho unitário e só modifica a fase. Mas a opção mais utilizada é aumentar
a ordem do filtro, assim, a atenuação será mais eficiente. (FILHO, 2010)
2.2 Reposta do sinal em frequência
O soma de senoides da figura 3 é mostrada na figura 4
A transformada rápida de Fourier é mostrada na figura 5. Cada senoide contém
uma informação, de modo que no domínio da frequência possuem um pico que são as
Magnitude(dB)
-40
-30
-20
-10
0
10-2
10-1
100
101
102
Phase(deg)
-90
-45
0
Bode Diagram
Frequency (rad/s)
Figura 4 – Diagrama de Bode do filtro passa baixas.

12. Capítulo 2. Simulações 11
Figura 5 – Soma de senoides graficamente no Psim.
Figura 6 – Resposta do sinal em frequência.
harmônicas.
Poderíamos ter feito essa análise utilizando o MATLAB através da função "fftn"que
calcula a transformada rápida de Fourier normalizada.
2.2.1 Sinal Filtrado
Poderíamos querer atenuar as frequências maiores que uma dada frequência de
corte, 3k Hz, por exemplo. Se R = 100 Ω, RL = 18790,89 Ω e C = 22 µF podemos
atenuar frequências maiores que 3k Hz. A função de transferência fica:
H(s) =
454, 5
s + 457

13. Capítulo 2. Simulações 12
Figura 7 – Comparação do sinal normal com o filtrado para 3k Hz.
Figura 8 – Comparação sinal normal com o filtrado para 5k Hz.
e o resultado é mostrado na figuras 7, que mostra que, na frequência de corte de
3k Hz o filtro não atenua. Para 5k Hz, o filtro começa a atenuar.

14. 13
3 Conclusão
Tendo em vista o exposto, podemos constatar que filtros de primeira ordem não são
tão eficientes, pois, além de defasarem muito o sinal não tem uma atenuação muita rápida.
Com isso, se projetássemos um filtro de segunda ordem, teríamos um novo parâmetro,
chamado fator de qualidade. Quando maior este parâmetro, mais seletivo na filtragem
nosso filtro seria.

15. 14
Referências
FILHO, S. N. Filtros seletores de sinais. Santa Catarina: UFSC, 2010. Citado na página
10.
OGATA, K. Engenharia de controle moderno. 5. ed. [S.l.]: Pearson Education, 2010.
Citado na página 7.