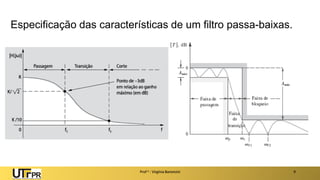
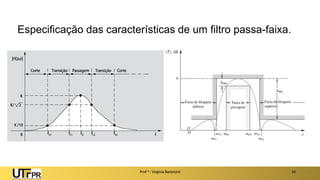
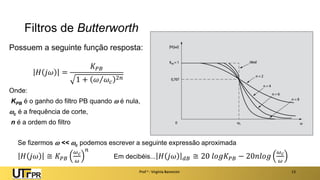
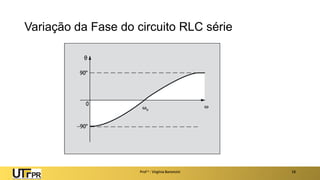
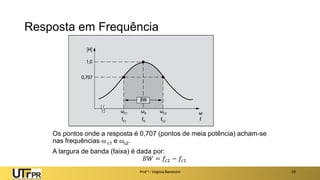
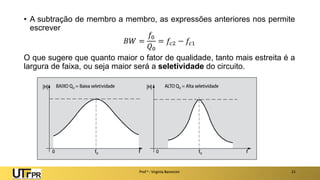
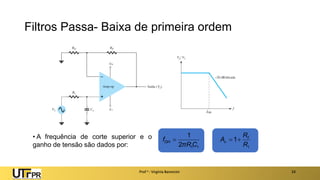
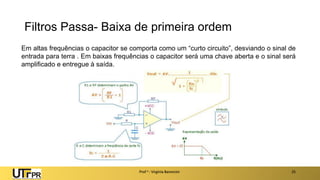
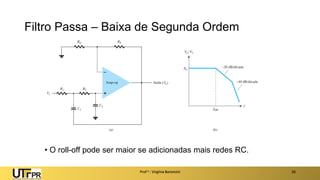
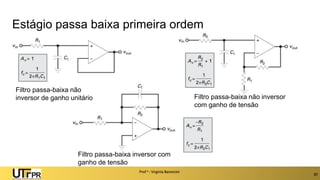
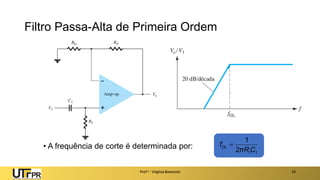
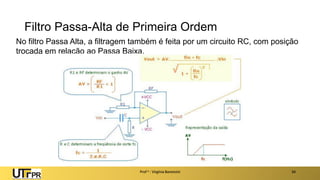
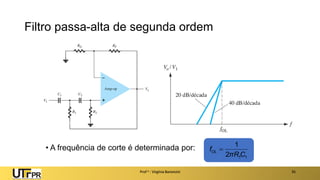
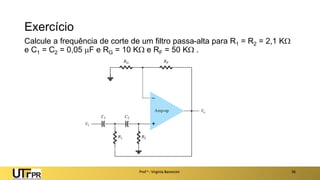
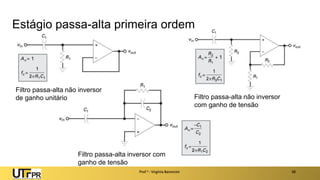
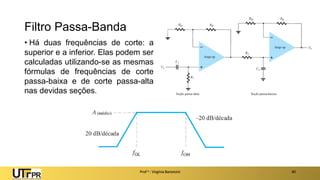
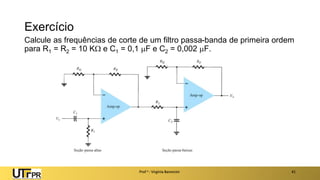
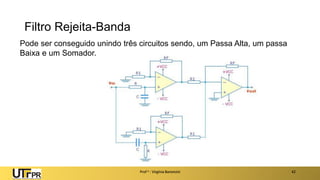
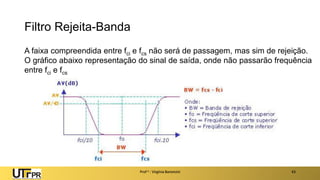
O documento apresenta uma introdução aos filtros ativos, destacando a diferença entre filtros passivos e ativos, suas vantagens e desvantagens. Os filtros são classificados em várias categorias, incluindo passa-baixa, passa-alta e rejeita-faixa, com especificações relacionadas à frequência de corte e ganho. Além disso, aborda a implementação de filtros digitais e a aplicação de amplificadores operacionais na construção de filtros ativos.

1. Filtros Ativos

2. Introdução
• Quase todos os sistemas de comunicação usam filtros.
• Um filtro permite a passagem de uma faixa de frequências enquanto
rejeita outra.
• Os filtros podem separar os sinais desejados dos indesejados, bloquear
sinais de interferência, melhorar sinais de voz e vídeo e modificar sinais
• Um filtro pode ser passivo ou ativo.
Prof a : Virgínia Baroncini 2

3. Filtros Ativos x Passivos
Passivos
• São aqueles construídos apenas
com elementos passivos, como
resistores, capacitores e indutores.
• São inviáveis em baixas
frequências, pois exigem indutores
muito grandes.
• São em geral usados acima de 1
MHz, não têm ganho de potência e
são relativamente difíceis de serem
sintonizados.
Ativos
• São aqueles construídos com
elementos passivos associados a
elementos ativos (válvulas,
transistores ou amplificadores
operacionais).
• São úteis abaixo de 1 MHz, têm
ganho de potência e são fáceis de
serem sintonizados.
Prof a : Virgínia Baroncini 3

4. Vantagens dos Filtros Ativos
• Eliminação de indutores, os quais em baixas frequências são volumosos,
caros e pesados;
• Facilidade de projeto de filtros complexos através da associação em
cascata de estágios simples;
• possibilidade de se obter grande amplificação do sinal de entrada
(ganho), principalmente quando este for um sinal de nível muito baixo;
• Grande flexibilidade de projetos;
Prof a : Virgínia Baroncini 4

5. Desvantagens dos Filtros Ativos
• Exigem fonte de alimentação.
• A resposta em frequência dos mesmos está limitada á capacidade de
resposta dos AOPs utilizados;
• Não podem ser aplicados em sistemas de média e alta potência;
Prof a : Virgínia Baroncini 5

6. Classificação dos Filtros
Prof a : Virgínia Baroncini 6
Passa Baixa ⇒ Ao contrário do Passa Alta só permite a passagem de baixas
frequências, atenuando frequências acima da corte.
Passa Alta ⇒ Permite a passagem de frequências acima da frequência de corte

7. Classificação dos Filtros
Prof a : Virgínia Baroncini 7
Passa faixa⇒ Permite passagem de frequências entre dois valores de frequência
pré-estabelecidos pelo projetista.
Rejeita faixa ⇒ Bloqueia frequências intermediárias, enquanto permite a passagem de
frequências inferiores de superiores à banda não permitida.

8. Especificação do Filtro
A transmissão de um filtro é definida por 4 parâmetros:
1- borda na faixa de passagem: fp
2- borda na faixa de bloqueio: fs
3- máxima variação do ganho permitida na faixa de passagem: Amax
4- atenuação mínima necessária para a faixa de bloqueio: Amin
• A partir desses parâmetros é montado o gabarito do filtro, dentro do qual
deve estar contida sua resposta em frequência
Prof a : Virgínia Baroncini 8

9. Prof a : Virgínia Baroncini 9
Especificação das características de um filtro passa-baixas.

10. Prof a : Virgínia Baroncini 10
Especificação das características de um filtro passa-faixa.

11. Filtros Digitais
• Um sinal analógico é convertido em sinais digitais através de um sistema
de conversão analógico-digital. O sinal binário representativo de entrada,
obtido pelo processo citado, é filtrado pelo filtro digital e o resultado é
reconvertido em sinal analógico por um sistema de conversão digital-
analógico.
Prof a : Virgínia Baroncini 11

12. Classificação através da Aproximação utilizada
Um outro aspecto de classificação dos filtros diz à respeito à aproximação
utilizada para projetá-los, exigindo um tratamento matemático complexo e
puramente teórico. Os tipos mais comuns são:
• Butterworth;
• Chebyshev;
• Cauer;
Cada uma dessas aproximações possui uma função matemática específica
através da qual se consegue obter uma curva de resposta aproximada para
um determinado tipo de filtro.
Prof a : Virgínia Baroncini 12

13. Filtros de Butterworth
Possuem a seguinte função resposta:
𝐻 𝑗𝜔 =
𝐾𝑃𝐵
1 + 𝜔 𝜔𝑐
2𝑛
Onde:
KPB é o ganho do filtro PB quando  é nula,
c é a frequência de corte,
n é a ordem do filtro
Prof a : Virgínia Baroncini 13
Se fizermos  << c podemos escrever a seguinte expressão aproximada
𝐻 𝑗𝜔 ≅ 𝐾𝑃𝐵
𝜔𝑐
𝜔
𝑛
Em decibéis... 𝐻 𝑗𝜔 𝑑𝐵 ≅ 20 𝑙𝑜𝑔𝐾𝑃𝐵 − 20𝑛𝑙𝑜𝑔
𝜔𝑐
𝜔

14. Filtros de Chebyshev
Possuem a seguinte função resposta:
𝐻 𝑗𝜔 =
𝐾𝑃𝐵
1 + 𝐸2𝐶𝑛
2
𝜔 𝜔𝑐
Onde:
KPB é o ganho do filtro PB quando  é nula,
c é a frequência de corte,
E é uma constante que define a amplitude
dos ripples presentes na faixa de passagem
Cn é chamado de polinôminio de Chebyshev
Prof a : Virgínia Baroncini 14

15. Filtros de Cauer ou elípticos
• Esses filtros apresentam ripples
tanto na faixa de passagem como
na faixa de corte.
• São os que tem a melhor definição
em termos de frequência de corte,
isto é, a faixa de transição é
estreita
Prof a : Virgínia Baroncini 15

16. Ressonância, Fator Q0 e seletividade
Prof a : Virgínia Baroncini 16
• Baseando num circuito RLC...
A impedância de entrada é dada por :
𝑍𝑖 = 𝑅 + 𝑗 𝜔𝐿 −
1
𝜔𝐶

17. Prof a : Virgínia Baroncini 17
Diz-se que o circuito está em ressonância–série 𝑍𝑖 𝜔
quando é real, ou seja:
𝜔𝐿 −
1
𝜔𝐶
= 0.
ou
𝜔0 =
1
𝐿𝐶
→ 𝑍𝑖 = 𝑅
e portanto teremos a máxima corrente.

18. Variação da Fase do circuito RLC série
Prof a : Virgínia Baroncini 18

19. Resposta em Frequência
Prof a : Virgínia Baroncini 19
Os pontos onde a resposta é 0,707 (pontos de meia potência) acham-se
nas frequências  c1 e c2.
A largura de banda (faixa) é dada por:
𝐵𝑊 = 𝑓𝑐2 − 𝑓𝑐1

20. Fator de Qualidade
• Um fator de qualidade,𝑄0 = 𝜔0
𝐿
𝐶 , pode ser definido para o circuito RLC
série, quando em ressonância. As frequências de meia potência podem
ser expressas em termos dos elementos do circuito:
𝜔𝑐2 = 𝜔0 1 +
1
4𝑄0
2 +
1
2𝑄0
𝜔𝑐1 = 𝜔0 1 +
1
4𝑄0
2 −
1
2𝑄0
Prof a : Virgínia Baroncini 20

21. • A subtração de membro a membro, as expressões anteriores nos permite
escrever
𝐵𝑊 =
𝑓0
𝑄0
= 𝑓𝑐2 − 𝑓𝑐1
O que sugere que quanto maior o fator de qualidade, tanto mais estreita é a
largura de faixa, ou seja maior será a seletividade do circuito.
Prof a : Virgínia Baroncini 21

22. Exercício
Num circuito RLC série, a frequência de ressonância é igual a 3KHz, e o
fator de qualidade é igual a 15. Pede-se:
• as frequências de corte inferior e superior.
• a largura de faixa do circuito
Prof a : Virgínia Baroncini 22

23. Filtros Ativos
• Os amp-ops também são empregados na montagem de filtros ativos.
• Um filtro pode ser construído utilizando-se componentes passivos:
resistores e capacitores.
• Um filtro ativo também possui um amplificador para produzir amplificação
de tensão e buferização ou isolamento do sinal.
• Adicionar capacitores aos circuitos amp-op fornece controle externo das
frequências de corte. O filtro ativo do amp-op tem ganho de frequências
de corte controlável.
Prof a : Virgínia Baroncini 23

24. Filtros Passa- Baixa de primeira ordem
Prof a : Virgínia Baroncini 24
1
1
2
1
C
πR
fOH 
1
1
R
R
A f
v 

• A frequência de corte superior e o
ganho de tensão são dados por:

25. Filtros Passa- Baixa de primeira ordem
Prof a : Virgínia Baroncini 25
Em altas frequências o capacitor se comporta como um “curto circuito”, desviando o sinal de
entrada para terra . Em baixas frequências o capacitor será uma chave aberta e o sinal será
amplificado e entregue à saída.

26. Filtro Passa – Baixa de Segunda Ordem
Prof a : Virgínia Baroncini 26
• O roll-off pode ser maior se adicionadas mais redes RC.

27. Prof a : Virgínia Baroncini 27
• O filtro passa baixas simples tem, além da banda passante, uma inclinação de
apenas 20 dB/década; ou seja, a atenuação provida pelo filtro aumenta em dez
vezes quando a frequência aumenta por um fator de dez.
• A conexão de dois estágios como este em cascata pode aumentar a inclinação para
40 dB/década: a atenuação provida pelo filtro aumentaria em cem vezes se a
frequência aumentar por um fator de dez.

28. Exercício
Calcule a frequência de corte de um filtro passa-baixa de primeira ordem
para R1 = 1,2 K e C=0,02 F.
Prof a : Virgínia Baroncini 28

29. Projeto de filtro PB de primeira ordem
Prof a : Virgínia Baroncini 29
Esse circuito apresenta um ganho K dado por :
𝐾 = 1 +
𝑅3
𝑅2
Por outro lado, é interessante minimizar o
efeito de tensão de offset de entrada, impondo
a relação:
𝑅1 =
𝑅2𝑅3
𝑅2 + 𝑅3
Pode ser demostrado que R1 está relacionado com a frequência de corte através da seguinte
fórmula:
𝑅1 =
1
𝑏𝜔𝐶𝐶
Onde b é um parâmetro que irá determinar o tipo de função resposta para os filtros de ordem
ímpar ≥ 3.

30. Estágio passa baixa primeira ordem
Prof a : Virgínia Baroncini
30
Filtro passa-baixa não inversor
com ganho de tensão
Filtro passa-baixa não
inversor de ganho unitário
Filtro passa-baixa inversor com
ganho de tensão

31. Exercício
Calcule o ganho e a frequência de corte do filtro abaixo
Prof a : Virgínia Baroncini 31

32. Exercício
Calcule o ganho e a frequência de corte do filtro abaixo
Prof a : Virgínia Baroncini 32

33. Filtro Passa-Alta de Primeira Ordem
Prof a : Virgínia Baroncini 33
1
1
2
1
C
πR
fOL 
• A frequência de corte é determinada por:

34. Filtro Passa-Alta de Primeira Ordem
Prof a : Virgínia Baroncini 34
No filtro Passa Alta, a filtragem também é feita por um circuito RC, com posição
trocada em relação ao Passa Baixa.

35. Filtro passa-alta de segunda ordem
Prof a : Virgínia Baroncini 35
1
1
2
1
C
πR
fOL 
• A frequência de corte é determinada por:

36. Exercício
Calcule a frequência de corte de um filtro passa-alta para R1 = R2 = 2,1 K
e C1 = C2 = 0,05 F e RG = 10 K e RF = 50 K .
Prof a : Virgínia Baroncini 36

37. Projeto do filtro PA de primeira ordem
Prof a : Virgínia Baroncini 37
As equações de projeto desse filtro são as seguintes:
𝐾 = 1 +
𝑅3
𝑅2
e 𝑅1 =
1
𝑏𝜔𝐶𝐶
Onde b deve ser obtido nas tabelas apropriadas de
filtros de ordem ímpar ≥ 3, pois, para filtros PA de
primeira ordem, tem-se sempre b=1.
𝑅2 =
𝐾𝑅1
𝐾 − 1
Se K=1, R2 deverá ser “aberto” e R3 será em curto

38. Estágio passa-alta primeira ordem
Prof a : Virgínia Baroncini 38
Filtro passa-alta não inversor
com ganho de tensão
Filtro passa-alta inversor com
ganho de tensão
Filtro passa-alta não inversor
de ganho unitário

39. Filtro Passa Banda
Prof a : Virgínia Baroncini 39
O filtro passa banda pode ser construído unindo um filtro Passa Alta e um Passa Baixa.

40. Filtro Passa-Banda
Prof a : Virgínia Baroncini 40
• Há duas frequências de corte: a
superior e a inferior. Elas podem ser
calculadas utilizando-se as mesmas
fórmulas de frequências de corte
passa-baixa e de corte passa-alta
nas devidas seções.

41. Exercício
Calcule as frequências de corte de um filtro passa-banda de primeira ordem
para R1 = R2 = 10 K e C1 = 0,1 F e C2 = 0,002 F.
Prof a : Virgínia Baroncini 41

42. Filtro Rejeita-Banda
Prof a : Virgínia Baroncini 42
Pode ser conseguido unindo três circuitos sendo, um Passa Alta, um passa
Baixa e um Somador.

43. Filtro Rejeita-Banda
Prof a : Virgínia Baroncini 43
A faixa compreendida entre fci e fcs não será de passagem, mas sim de rejeição.
O gráfico abaixo representação do sinal de saída, onde não passarão frequência
entre fci e fcs