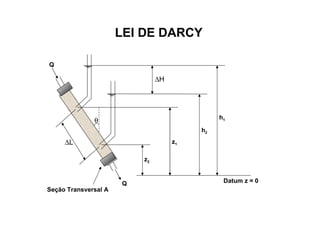
1) A lei de Darcy demonstra que a descarga de água subterrânea (Q) é igual ao produto da condutividade hidráulica (K), gradiente hidráulico (I) e área da seção (A). 2) Se a porosidade é n, então a velocidade aparente da água é igual a KI dividido por n. 3) Para o aquífero em questão, a descarga é de 0,12 m3/segundo e o tempo para a água se deslocar entre os poços 1km distantes é de cerca

1. LEI DE DARCY Demonstrou que a descarga Q de água subterrânea pode ser definida como o produto de seção perpendicular ao fluxo (A), o gradiente hidráulico (I) e a condutividade hidráulica  Q = K.I.A A unidade de cada lado da equação é uma taxa de fluxo volumétrico como m 3 /dia e esta relação é conhecida como lei de Darcy. A quantidade Q/A = KI é o fluxo de Darcy (v), onde: v = Q/A ou Q = v.A V é uma velocidade aparente pois o fluido tem que se deslocar através dos espaços porosos. Se a porosidade é n então a seção perpendicular ao fluxo é An e vx = Q/An ou vx = KI/n

2. LEI DE DARCY Datum z = 0 z 2 z 1 h 2 h 1  Q Q  H  L Seção Transversal A