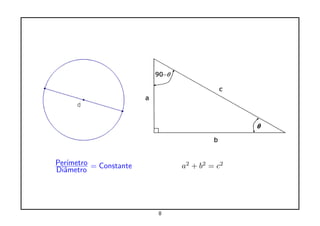
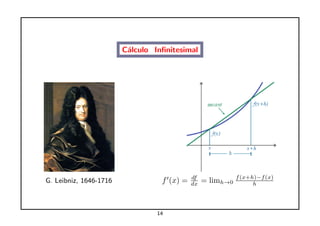
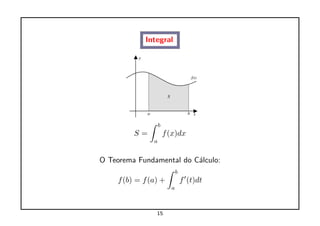
O documento explora a interseção entre matemática e física, destacando a importância da matemática como linguagem para descrever leis físicas. Cita contribuições de figuras históricas como Galileo, Newton e Einstein, enfatizando o papel da matemática na formulação de teorias científicas. Além disso, discute conceitos como cálculo, equações diferenciais e a aplicabilidade matemática à realidade.

1. A Matem´tica da F´
a ısica
Rotas Matem´ticas da UTL 2012
a
Jorge Drumond Silva
Departamento de Matem´tica
a
Instituto Superior T´cnico
e
jsilva@math.ist.utl.pt
1

2. ”Como ´ poss´ que a matem´tica, sendo afinal de contas um produto da
e ıvel a
mente humana independente da experiˆncia, seja t˜o admiravelmente
e a
apropriada ` descri¸˜o dos objectos da realidade.” - Albert Einstein
a ca
”O milagre da matem´tica ser a linguagem apropriada para a formula¸˜o das
a ca
leis da f´
ısica, ´ uma d´diva maravilhosa que n˜o entendemos nem merecemos.
e a a
Devemos estar gratos por ele e esperar que se mantenha v´lido na investiga¸˜o
a ca
futura, e que se extenda para nosso prazer, apesar talvez da nossa admira¸˜o, a
ca
outros ramos do conhecimento.” - Eugene Wigner
2

3. Matem´tica Avan¸ada Pr´-hist´rica
a c e o
3

4. E Mais Matem´tica Avan¸ada ...
a c
4

5. Caracter´
ısticas da Matem´tica/F´
a ısica Pr´-Hist´rica
e o
Quantitativa
Deterministica
Abstracta
⇓ (Racioc´ L´gico Dedutivo)
ınio o
Previsibilidade
5

6. Geometria
Etimologia: geo-metri = medi¸˜o da terra
ca
6

7. Gr´cia Antiga
e
Rafael, A Escola de Atenas (Causarum Cognitio), 1510
7

8. Per´
ımetro = Constante a2 + b2 = c2
Diˆmetro
a
8

9. Euclides e os Elementos
Euclides de Alexandria, aprox. 300 A.C. Papiro dos Elementos, aprox. 100 D.C.
9

10. 10

11. Galileo Galilei
Galileo Galilei, 1564-1642
11

12. M´todo Cient´
e ıfico
”A Filosofia est´ escrita neste grandioso livro - isto ´, o universo - o qual est´
a e a
permanentemente aberto ` nossa observa¸˜o, mas que n˜o pode ser
a ca a
compreendido sem que primeiro se aprenda a linguagem e se interpretem os
s´
ımbolos em que est´ escrito. Ele est´ escrito na linguagem da matem´tica, e
a a a
os seus s´
ımbolos s˜o triˆngulos, circunferˆncias e outras figuras geom´tricas,
a a e e
sem as quais ´ humanamente imposs´ perceber uma unica palavra que seja
e ıvel ´
dele.”
Galileo Galilei
• Observa¸˜es e medi¸˜es
co co
• Formula¸˜o de hip´tese e constru¸˜o de teoria ou modelo matem´tico
ca o ca a
• Dedu¸˜o l´gica e previs˜o de consequˆncias da teoria
ca o a e
• Teste experimental das previs˜es
o
12

13. Isaac Newton
Isaac Newton, 1643-1727 C´pia da primeira edi¸˜o de Principia Mathematica do
o ca
pr´prio Newton
o
13

14. C´lculo Infinitesimal
a
df f (x+h)−f (x)
G. Leibniz, 1646-1716 f (x) = dx = limh→0 h
14

15. Integral
b
S= f (x)dx
a
O Teorema Fundamental do C´lculo:
a
b
f (b) = f (a) + f (t)dt
a
15

16. Equa¸˜es Diferenciais
co
Problema
Descobrir a traject´ria no tempo x(t), da part´
o ıcula de massa m, tal que:

m d22 = F (t, x(t), x (t))
 dtx




x(0) = posi¸˜o inicial
 ca



x (0) = velocidade inicial
16

17. Matem´tica e F´
a ısica
”As far as the laws of mathematics refer to reality, they are not certain; and as
far as they are certain, they do not refer to reality.” - Albert Einstein
17