Curso de estatística básica

GIOVANI GLAUCIO DE OLIVEIRA COSTA
Curso de Estatística Básica:
Teoria e Prática
2ª Edição
EDITORA ATLAS
SÂO PAULO, 2013
1

Agradecimentos:
À minha mãezinha querida, Oneida Barreto de Campos
Costa; Aos meus irmãos amigos e companheiros André
Luiz de Oliveira Costa e Andréa Viviane de Oliveira Costa;
à minha afilhadinha e sobrinha amada Juliana Paula Costa
Lima e a Editora Atlas pela confiança que depositou em
meu trabalho.
2

Prefácio
Este livro é o resultado de experiências vividas a partir de 1991, quando
iniciei a minha vida acadêmica como docente de graduação das Faculdades
Cândido Mendes em Campus do Goitacazes no Estado do Rio de Janeiro. A
partir daí o material didático que utilizava para lecionar Estatística foi se
aperfeiçoando com a prática adquirida em outras instituições de ensino
superior, tais como a Universidade Salgado de Oliveira, a Universidade Federal
do Rio de Janeiro, a Universidade da Cidade, a Universidade Federal
Fluminense, dentre muitas outras, até terminar nos últimos quatro anos com a
Universidade Federal Rural do Rio de Janeiro. Foi também testado em cursos
de especialização e mestrado em economia e administração, sendo
apresentado como texto para contemplar diversos programas.
Essa soma de cursos e experiências mostrou que a melhor maneira de
apresentar a matéria é a de expor os assuntos de maneira objetiva, prática e
instrumental, onde os conceitos são contextualizados dentro da área de
formação de cada curso ou estudante. Este recurso didático é importante
porque motiva e impulsiona o gosto pela disciplina pelos estudantes.
Procuro, na maioria dos casos, apresentarem os conceitos sucintamente
de maneira a ser usado imediatamente na empresa ou em situações de
pesquisas, sem grandes demonstrações matemáticas ou formalismos. Logo em
seguida, os exemplifico através de “cases” práticos, reais em diversas áreas
negócios, saúde e engenharias. São disponibilizados exercícios propostos no
final de cada unidade.
O presente livro se destina a cursos de estatística em nível básico ou
introdutório em áreas predominantemente de ciências humanas e sociais. O
seu conteúdo objetiva dar uma visão geral e instrumental de estatística
descritiva e suas aplicações nestas áreas. Para tanto, versa sobre conceitos
básicos de estatística, variáveis, noções de amostragem, fases do método
estatístico, séries estatísticas, números relativos, gráficos estatísticos, estudo
3

das distribuições de frequências, números-índices e análise exploratória de
dados(EAD).
No final do livro, em anexos, são apresentados textos auxiliares que
completam o entendimento e aplicação dos conceitos e exercícios:
arredondamento de dados, normas de representação tabular e como construir
uma distribuição de frequência por classes.
As áreas e os cursos de aplicação deste livro são amplos e muito
diversificados em cursos de estatística de nível básico, mas podemos destacar
a adoção deste compêndio em disciplinas de estatística básica ou introdutória
de cursos de Administração, Economia, Turismo, Educação, Saúde, e também
em programas de pós-graduação especialização e mestrado, como
nivelamento.
Gostaria muito de contar com a ajuda de todos os leitores, alunos e
colegas para avaliação crítica positiva deste texto, de modo que possamos
evoluir em qualidade, superando os erros e aperfeiçoando os acertos. Será
muito gratificante para mim se meu livro tiver sido de alguma forma útil para o
leitor, nem que tenha sido em somente um parágrafo e/ou em somente uma
página, mas espero de verdade que ele seja relevante em todo o seu conteúdo.
Obrigado a todos e boa leitura.
O autor.
4

Sumário
Capítulo 1 : Conceitos Básicos de Estatística...............................................
Fenômeno..........................................................................................................
Ciência...............................................................................................................
Ciência Estatística.............................................................................................
Fenômeno Coletivo ou de Massa......................................................................
População..........................................................................................................
Amostra..............................................................................................................
Levantamentos Estatísticos...............................................................................
Censo.................................................................................................................
Amostragem.......................................................................................................
Razões para o Uso da Amostragem...................................................................
Importância da Amostra......................................................................................
Divisão da Estatística.........................................................................................
Estatística Descritiva..........................................................................................
Estatística Inferencial.........................................................................................
Esquema Lógico de um Estudo Estatístico.......................................................
Exercícios Propostos.........................................................................................
Capítulo 2: Variáveis.......................................................................................
Conceito de Variáveis........................................................................................
Tipos de Variáveis.............................................................................................
Variáveis Qualitativas........................................................................................
Variável Qualitativa Nominal..............................................................................
Variável Qualitativa Ordinal...............................................................................
Variáveis Quantitativas......................................................................................
Variável Quantitativa Discreta............................................................................
Variável Quantitativa Contínua..........................................................................
Resumo do Conceito de Variáveis.....................................................................
5

Capítulo 3: Noções de Amostragem.............................................................
Conceitos de Amostragem.................................................................................
Amostragens Probabilísticas.............................................................................
Tipos de Amostragem Probabilística.................................................................
Amostragem Aleatória Simples.........................................................................
Amostragem Sistemática..................................................................................
Amostragem Estratificada..................................................................................
Amostragem por Conglomerados......................................................................
Amostragens Não-Probabilísticas......................................................................
Tipos de Amostragens Não-Probabilísticas.......................................................
Inacessibilidade a Toda População...................................................................
Amostragem a Esmo ou Sem Norma................................................................
População Formada de Material Contínuo........................................................
Amostragem Intencional....................................................................................
Amostragem por Voluntários.............................................................................
Amostragem por Quotas....................................................................................
Tamanho de Amostras para Estimação de Proporções Populacionais em
Pesquisas..........................................................................................................
População Finita e Infinita..................................................................................
Tamanho de Amostras em Amostragem Aleatória Simples..............................
Cálculo de Tamanho da Amostra Alternativo....................................................
Tamanho de Amostras em Amostragem Estratificada ou por Quotas...............
Amostragem por Quotas Versus Amostragem Aleatória Estratificada..............
Capítulo 4: Fases do Método Estatístico......................................................
Método...............................................................................................................
Método Estatístico.............................................................................................
Fases do Método Estatístico..............................................................................
6

Planejamento.........................................................................................................
Necessidade(Relevância) da Pesquisa.................................................................
Definição das Variáveis da Pesquisa.....................................................................
Definição da Necessidade da Pesquisa com Trabalho de Campo........................
Pesquisa com Trabalho de Campo........................................................................
Projetos de Pesquisa.............................................................................................
Coletas de Dados(Trabalho de Campo)................................................................
Fonte de Dados em Pesquisas..........................................................................
Tipos de Dados em Pesquisas..........................................................................
Sequência no Processo de Dados em Pesquisas.............................................
Crítica de Dados................................................................................................
Apuração de Dados...........................................................................................
Análise de Dados...............................................................................................
Emissão do Relatório Final................................................................................
Comunicação dos Resultados...........................................................................
Capítulo 5: Séries Estatísticas.......................................................................
Conceitos de Séries Estatísticas.......................................................................
Séries Temporais...............................................................................................
Séries Geográficas............................................................................................
Séries Especificativas........................................................................................
Séries Mistas.....................................................................................................
Distribuições de Freqüência..............................................................................
Capítulo 6– Números Relativos
Dados Absolutos.................................................................................................
Dados Relativos...................................................................................................
Coeficientes..........................................................................................................
Taxas...................................................................................................................
7

Percentagens......................................................................................................
Índices..................................................................................................................
Exercícios Propostos.............................................................................................
Capítulo 7: Gráficos Estatísticos..................................................................
Conceito de Gráficos Estatísticos......................................................................
Requisitos Fundamentais de um Gráfico...........................................................
Finalidades dos Gráficos...................................................................................
Tipos de Gráficos...............................................................................................
Gráficos de Reclame.........................................................................................
Tipos de Gráficos de Reclame...........................................................................
Construção dos Gráficos...................................................................................
Gráfico Linear ou de Linha.................................................................................
Gráfico de Colunas............................................................................................
Gráfico de Barras...............................................................................................
Gráfico de Setores ou “Pizza”............................................................................
Interpretação de Gráficos de Reclame..............................................................
Gráficos de Análise............................................................................................
Tipos de Gráficos de Análise.............................................................................
Interpretação de Gráficos de Análise.................................................................
Histograma.........................................................................................................
Polígono de Frequência....................................................................................
Capítulo 8: Estudo das Distribuições de Freqüências...............................
Conceitos de Medidas de Distribuições de Frequências...................................
Medidas de Tendência Central..........................................................................
Medidas de Posição(Separatrizes)....................................................................
Medidas de Dispersão.....................................................................................
Medidas da Forma de uma Distribuição..........................................................
Exercícios Propostos.......................................................................................
8

Unidade 9: Números-Índices.........................................................................
Conceitos de Números-Índices.........................................................................
Números-Índices Simples ou Relativos............................................................
Relativos de Base Móvel(Elos Relativos).........................................................
Relativos de Base Fixa(Relativos em Cadeia)..................................................
Número-Índice Agregado ou Número-Índice Composto...................................
Número-Índice Agregativo Simples..................................................................
Número-Índice Agregativo Ponderado..............................................................
Construção de Índices de Preços....................................................................
Taxas de Inflação............................................................................................
Indicadores de Inflação...................................................................................
Deflacionamento de Dados..............................................................................
Taxa Média de Crescimento Anual.................................................................
Exercícios Propostos.......................................................................................
Unidade 10: Análise Exploratória de Dados....................................................
Introdução........................................................................................................
Conceito............................................................................................................
Importância da AED.........................................................................................
Gráfico de Caule-e-Folhas.................................................................................
Gráfico de Extremos-e-Quartis ou Caixa-com-Bigodes....................................
Gráfico de Probabilidade(P-P)............................................................................
Gráfico de Ajustamento dos Resíduos..................................................................
Anexo : Textos Auxiliares.................................................................................
Texto 1: Arredondamento de Dados.....................................................................
Texto 2: Normas de Representação Tabular........................................................
Texto 3: Construção de Distribuições de Frequência com Intervalos de Classes
Bibliografia...........................................................................................................
9

Unidade I
Conceitos Básicos de Estatística
Fenômeno:
É tudo que pode ser percebido pelos sentidos ou pela consciência.
Exemplos:
Uma fruta que cai de uma árvore, uma pessoa que nasce, uma mistura
de leite com café, a incidência de uma doença, o comportamento das pessoas
numa loja, o consumo de certo produto, a oferta de certo produto, a demanda
por certo produto, o lucro de uma empresa, o peso de uma criança ao nascer,
etc.
Ciência:
É o conjunto orgânico de conhecimentos sobre os fenômenos e suas
relações recíprocas.
Ciência Estatística:
A Estatística é a ciência que estuda um determinado tipo de fenômeno:
os fenômenos coletivos ou de massa. È, então, o conjunto de métodos e
processos quantitativos que serve para estudar e medir os fenômenos coletivos
ou de massa.
10

Fenômenos Coletivos ou de massa:
São os que não possuem regularidade na observação de casos
isolados, mas na massa de observações.
Exemplo:
Em geral, quando estudamos uma ou mais características de um
conjunto de elementos, chamado população, estamos diante de um fenômeno
coletivo ou de massa: as notas em matemática dos alunos de uma turma, o
nível sócio econômico dos consumidores de um produto, renda dos
brasileiros, lucro de empresas cariocas, gênero dos torcedores de um
clube de futebol, oferta de certo produto por parte de empresas
fornecedoras e nível de demanda de empréstimos consignados por
servidores públicos.
População:
É o conjunto de elementos portadores de pelo menos uma característica
comum de interesse para ser estudado estatisticamente.
Exemplos:
 Num estudo sobre satisfação por certo serviço, a população
estatística é constituída por todos os consumidores deste serviço;
 Num estudo sobre hábitos de fumar de certa cidade, a população
será formada por todos os habitantes desta cidade;
 Num estudo sobre conteúdo dos e-mails´s de sua caixa-postal, o
conjunto de e-mails de sua caixa postal é uma população
estatística.
 Num estudo sobre a oferta de certo produto, a população alvo
11

pode ser constituída por estabelecimentos comerciais.
Amostra:
É um subconjunto finito da população, selecionada adequadamente para
representá-la.
Para que as conclusões sobre a população sejam fornecidas
adequadamente pelas amostras é necessário que elas sejam representativas
da população.
Amostras representativas são aquelas que são verdadeiras miniaturas
da população, isto é, têm todas as características da população, mas em
menor escala.
Para obtermos amostras representativas existem vários métodos de
extração, mas os mais eficazes são aqueles em que os elementos que vão
compor a amostra são selecionados por sorteio, aleatoriamente.
Exemplos:
 Num estudo sobre satisfação por certo serviço oferecido por uma
empresa, a amostra é constituída por parte dos clientes (aqueles que
utilizaram) deste serviço;
 Num estudo sobre hábitos de fumar de clientes de um hotel, a amostra
será formada por parte dos clientes desta empresa.
 Num estudo sobre conteúdo dos e-mails´s de sua caixa-postal, a
amostra será uma parte representativa do conjunto de e-mails de sua
caixa postal.
12

Levantamentos Estatísticos:
A Estatística possui dois tipos de levantamentos:
Censo
Amostragem
Censo:
Estudo de uma população com base em todos os seus elementos.
Exemplo:
No Brasil, o Instituto Brasileiro de Geografia e Estatística (IBGE) realizam,
de dez em dez anos, o traço do perfil demográfico e sócio-econômico da
população brasileira. O objetivo principal do levantamento é atualizar os
dados estatísticos populacionais no intuito de orientar políticas e ações
públicas com informações atualizadas sobre a população.
13

Outros Exemplos:
 Quando estudamos características de banco de dados relacionais
através do exame exaustivo de seus registros, estamos diante de um
censo;
 Quando estudamos o desempenho dos programas criados por
diferentes analistas de sistemas de uma grande empresa, periciando
todos os computadores alvo da pesquisa;
 Quando estudamos os motivos de exclusões de perfis do facebook
através da observação de todos os facebooks excluídos.
Amostragem:
É o estudo de uma população com base em uma parte representativa da
mesma, isto é, com base numa amostra.
Exemplos:
 Quando estudamos características de banco de dados relacionais
através do exame de uma parte representativa de seus registros,
estamos diante de uma amostragem;
 Quando estudamos o desempenho dos programas criados por
diferentes analistas de sistemas de uma grande empresa, periciando
uma amostra dos computadores alvo da pesquisa;
 Quando estudamos os motivos de exclusões de perfis do facebook
através da observação de amostra dos facebooks excluídos.
14

Razões para o Uso da Amostragem:
o A população é infinita, ou considerada como tal, não podendo, portanto
ser analisada na íntegra;
o Custo excessivo do processo de recolha e tratamento dos dados, como
resultado da grande dimensão da população ou da complexidade do
processo de caracterização de todos os elementos da população;
o Tempo excessivo do processo de recolha e tratamento dos dados,
conduzindo à obtenção de informação desatualizada;
o As populações são dinâmicas, de onde resulta que os elementos ou
objetos da população estão em constante renovação, de onde resulta a
impossibilidade de analisar todos os elementos desta população;
o Recolha de informação através de processos destrutivos (que, se
aplicada exaustivamente, conduziria à completa destruição da
população);
o Inacessibilidade a alguns elementos da população, por diversas causas.
Exemplos1
Como exemplo, temos o caso de uma fábrica de automóveis que, pelas
questões apontadas acima, não efetua inspeção e ensaios em 100% dos itens
que serão agregados ao automóvel, faz as verificações de qualidade e
conformidade em momentos específicos durante a produção, seja no início,
meio ou fim. Logo no início do processo produtivo, é efetuada uma
inspeção(usando técnicas de amostragem) dos lotes de produtos recebidos.
15

Exemplo 2:
Outro exemplo interessante do uso de técnicas de amostragem é o
manejo sustentável de áreas florestais com fins extrativistas. Neste caso, numa
floresta definem-se áreas de controle( a amostra), mede-se a densidade
florestal destas áreas e extrapola-se o resultado para toda a mata. Pode-se
assim conhecer com boa precisão o número de espécies vegetais encontradas
e sua idade média, dentro outros aspectos.
Importância da Amostra:
Portanto, se a constituição da amostra obedecer a determinadas
condições, a análise das características da amostra pode servir para se
conhecer como se comporta a característica na população.
Divisão da Estatística:
A Estatística se divide em dois ramos:
16

Estatística Descritiva:
É a parte da Estatística que tem o objetivo de descrever os dados
observados, isto é:
•Obtenção dos dados;
•Redução dos dado;.
•Representação dos dados.
É atributo da Estatística Descritiva a obtenção de algumas informações
como médias, proporções, dispersões, tendências, índices, taxas que resumem
e representam os fenômenos observados. Isto encerra as atribuições da
Estatística Descritiva.
No caso de ter se optado pelo estudo estatístico com amostras, a
Estatística estabelece técnicas para se afirmar se a estimativa obtida junto à
amostra é de qualidade. Este é o objetivo da Estatística Inferencial.
Estatística Inferencial:
É a parte da Estatística que tem o objetivo de estabelecer técnicas de
avaliar se a estimativa obtida junto à amostra é de qualidade, isto é, se está
próxima do valor do parâmetro populacional. Portanto, é a técnica de tomar o
parâmetro populacional pela estimativa, desde que ela seja de boa qualidade,
isto é, significante.
A estatística Inferencial tem o objetivo de estabelecer níveis de
confiança para a tomada de decisão de associar uma estimativa amostral a um
parâmetro populacional de interesse.
17

Exemplo 1:
Suponha que tivéssemos interesse na renda média dos habitantes de
uma cidade. Para investigar o seu valor, optou-se por um estudo por
amostragem. Na amostra colhida, verificou-se uma estimativa de R$ 800,00
para a renda dos habitantes da cidade. Com base nesta estimativa, o que se
pode dizer do parâmetro populacional correspondente?
Exemplo 2:
Suponha que tivéssemos interesse no salário médio dos funcionários de
uma empresa. Para investigar o seu valor optou-se por um estudo por
amostragem. Na amostra colhida, verificou-se uma estimativa para o salário
dos funcionários da empresa R$ 2000,00. Este valor é significante? Está
próximo do valor do salário de toda a população? É válido como parâmetro
populacional? Ou é fruto de erro amostral?
Exemplo 3:
Suponha que tivéssemos colhido uma amostra de 50 contracheques de
um total de 2000 funcionários de uma empresa, e obtivéssemos a
porcentagem de pessoas que tiveram descontos por falta ou atrasos num mês
considerado. É função da Estatística Inferencial verificar se este resultado
encontrado em 50 trabalhadores para os 2000 é de boa qualidade, isto é, é
significante.
18

Esquema Síntese de um Estudo Estatístico:
População
Amostra
Estatística
Descritiva
Inferência
Estatística
Nesta figura, temos uma população da qual é retirada uma amostra. Vê-
se a Estatística Descritiva sendo aplicada para descrever e resumir o que
ocorre na população ou na amostra. Quando a Estatística resume populações,
ela faz Amostragem. Quando resume características, faz Estatística
Descritiva e quando a(s) descritiva(s) está(ão) num contexto de amostragem,
é(são) gerada(s) estimativa(s). Esta(s) estimativa(s) deve(em) ser avaliada(s)
quanto à sua qualidade de estimação, aonde são feitos os Testes de
Significância.
Portanto, a amostragem resume populações e a Estatística Descritiva
resume características, gerando quase sempre estimativas.
Para você ter uma visão global das etapas envolvidas em um estudo
estatístico observe atentamente o esquema a seguir:
19

Esquema Lógico de um Estudo Estatístico:
ALVO
POPULAÇÃO
ESTATÍSTICAS DESCRITIVAS:
PARÂMETROS
AMOSTRA ALEATÓRIA
CÁLCULO DE ESTIMATIVAS
DE PARÂMETROS
CÁLCULO DAS
PROBABILIDADES
ESTATÍSTICA INFERENCIAL:
TESTES DE SIGNIFICÂNCIA
TOMADA DE DECISÃO
20

Conclusão:
Este esquema mostra que o estudo estatístico se inicia na população,
passa pelas etapas amostragem, geração de estimativas, testes de
significância, e, é finalizado na tomada de decisão em uma contexto de
incerteza, mas que foi devidamente embasada pela metodologia estatística,
envolvida na análise, fato que irá lhe assegurar maior credibilidade.
Testes de significância são aqueles nos informam, com certa
segurança, se a estimativa gerada por uma amostra particular é ou não é fruto
de um erro de amostragem muito grande, orientando o pesquisador na decisão
de tomar o valor do parâmetro populacional por esta estatística disponível.
21

Exercícios Propostos
Responda às questões abaixo:
1. O que é Ciência?
2. O que é Estatística?
3. Explique o que você entende pôr população e amostra?
4. Qual o objetivo da Estatística Descritiva?
5. Qual o objetivo da Estatística Inferencial? Dê exemplos práticos.
6. O que você entende por censo?
7. O que você entende por amostragem?
8. Para que as conclusões sejam válidas, como devem ser as amostras?
9. Para que as amostras sejam representativas da população em estudo,
como devem se extraídos os seus elementos?
10. Explique o esquema lógico de um estudo estatístico.
22

Unidade II
Variáveis
Conceito de Variável:
É uma característica de interesse que associamos à população para ser
estudada estatisticamente.
Exemplos:
Altura, idade, estado-civil e salário de entrevistados em uma pesquisa.
Tipos de Variáveis:
As variáveis podem ser de dois tipos:
Qualitativas e Quantitativas
Variáveis Qualitativas
Apresentam como possíveis resultados uma qualidade (ou atributo) do
elemento pesquisado.
Exemplos:
Sexo, cor, aparência, status social, etc.
As variáveis qualitativas se classificam em nominais e ordinais.
23

Variável Qualitativa Nominal:
Não existe nenhuma ordenação possível nas realizações das categorias.
Exemplos:
Sexo, cor, estado-civil, nacionalidade, etc.
Variável Qualitativa Ordinal:
Existe certa ordem ou hierarquia entre as realizações de cada variável.
Exemplos:
o Nível de instrução: superior > médio > fundamental
o Nível Sócio-Econômico: classe alta > classe média > classe baixa
Outras:
Cargo ocupado por funcionários em uma empresa, posto no serviço
militar, classificação de candidatos no serviço público.
Variáveis Quantitativas
São aquelas em que as possíveis realizações são valores numéricos.
Exemplos:
Idade, estatura e peso corporal.
As variáveis quantitativas se classificam em discreta e contínua.
24

Variável Quantitativa Discreta:
São aquelas que resultam de contagens. Só podem assumir valores
inteiros.
Exemplos:
Número de filhos de um paciente, salário, número de acidentes numa via
expressa, número de atendimentos em um posto de saúde, etc.
Variável Quantitativa Contínua:
São aquelas que resultam de medição. Não são necessariamente
inteiras, dependem da precisão adotada e do instrumento de medida.
25

Exemplos:
Idade (tempo de vida), quilômetros rodados de um automóvel, estatura e
peso corporal dos entrevistados em uma pesquisa de satisfação com produtos
da linha light.
Resumo do Conceito de Variáveis:
Nominal
Qualitativas
Ordinal
Variáveis
Discreta
Quantitativas
Contínua
26

Classifique as variáveis abaixo:
1. Cor dos olhos dos candidatos a modelos de uma agência.
2. Número de filhos de casais residentes em uma cidade.
3. Causas de acidentes de trabalho de funcionários de uma fábrica.
4. Salários de funcionários de uma empresa.
5. Renda de clientes de um banco.
6. Classificação num concurso público.
7. Nota atribuída por parte de donas de casa à satisfação com certo
eletrodoméstico de 0 a 5.
8. Peso de candidatos num concurso na área militar.
9. Estabelecimentos de saúde, públicos e particulares.
10. Estado-civil de entrevistados em uma pesquisa de opinião.
27

Unidade III
Noções de Amostragem
Conceitos de Amostragem:
oAmostragem é o processo de retirada de amostras;
oÉ o estudo de uma população com base em uma amostra
representativa;
o Amostra é uma parte da população, retirada segundo uma regra
conveniente;
o Existem vários tipos de amostragem, ou melhor, várias regras
para seleção de amostras;
o O pressuposto básico para que se utilize uma determinada
regra de amostragem é que ela gere amostras representativas, isto é,
com todas as características básicas e importantes do universo: que
seja uma verdadeira miniatura da população;
o Apresentaremos as principais regras para a retirada de uma
amostra;
o As regras de amostragem podem ser classificadas em duas
categorias gerais: probabilísticas e não- probabilísticas.
Amostragens Probabilísticas:
São amostragens em que a seleção é aleatória de tal forma que
cada elemento da população tenha uma chance real de fazer parte da
amostra.
Assim: se N define o tamanho da população e se todos os
elementos da população possuem igual probabilidade, teremos que 1/N
é a probabilidade de cada elemento participar da amostra.
28

Tipos de Amostragens Probabilísticas:
oAmostragem aleatória simples
oAmostragem sistemática
oAmostragem estratificada
oAmostragem por conglomerados
Amostragem Aleatória Simples:
Também conhecida por amostragem ocasional, causal, randômica etc. A
amostragem aleatória simples destaca-se por ser um processo de seleção
bastante fácil e muito usado. Neste processo, todos os elementos da
população têm igual probabilidade de serem escolhidos, não soantes de ser
iniciado, como até completar-se o processo de coleta.
Eis o procedimento para seu uso:
1o
. Devemos numerar todos os elementos da população. Se, por
exemplo, nossa população tem 5000 elementos, devemos numerá-los de 1 a
5000 ou, como acontece geralmente, usamos um número que identifica o
elemento.
2o
. Devemos efetuar sucessivos sorteios com ou sem reposição até
completar o tamanho da amostra (n).
Para realizar o sorteio de forma aleatória sugere-se o uso da planilha
eletrônica Excel, utilizando a função “ aleatório” ou em análise de dados a
opção “amostragem”. O processo termina quando for sorteado o último
elemento “n”.
29

Amostragem Sistemática
Trata-se de uma variação da amostragem simples, muito conveniente
quando a população está naturalmente ordenada, como fichas em um fichário,
listas telefônicas, clientes de uma empresa registrados em um banco de dados
etc.
Procedimento:
Se N o tamanho da população e n o tamanho da amostra. Então,
calcula-se o intervalo de amostragem N/n ou o inteiro mais próximo de “I”.
Sorteia-se, utilizando-se algum dispositivo aleatório qualquer (geração de
números aleatórios no Excel ou a tabela de números aleatórios) um número x
entre 1 e “I” formando-se amostra dos elementos correspondentes aos
números: x; x+I; x+2I; ... ; x+ (n-1)I.
Exemplo:
Seja N = 500 e n = 50. Então, 500/50 = 10 ou I = 10
Sorteia-se um número de 1 a 10. Seja 3, (x = 3) o número sorteado.
Logo, os elementos numerados por 3; 13; 23; 33; ...
Amostragem Estratificada
No caso de população heterogênea, na qual podemos distinguir
subpopulações mais ou menos homogêneas, denominadas estratos, podemos
usar a amostragem estratificada.
Estratificar uma população é dividi-la em L subpopulações denominadas
estratos, tais que N1 + N2 + ... +NL = N, onde os estratos são mutuamente
exclusivos.
Após a determinação dos estratos, seleciona-se uma amostra aleatória
de cada subpopulação.
30

Se as diversas subamostras tiverem tamanhos proporcionais ao
respectivos número de elementos no estrato, teremos a estratificação
proporcional.
Amostragem por Conglomerados:
Quando a população apresenta uma subdivisão em pequenos grupos
não necessariamente homogêneos, mas fisicamente próximos, podemos
chamar cada grupo de elementos fisicamente próximos de conglomerados e
realizar a amostragem por conglomerados.
Pode-se fazer a amostragem por conglomerados, a qual consiste em
sortear um número suficiente de conglomerados, cujos elementos constituirão
a amostra.
As unidades de amostragem sobre as quais é feito o sorteio passam a
ser o s conglomerados e não mais os elementos individuais da população.
Esse tipo de amostragem é às vezes adotado por motivos de ordem
prática e econômica, ou mesmo por razões de viabilidade: não é possível se
obter uma listagem da população numerada para realizar um sorteio, mas
é relativamente fácil se conseguir a listagem de conglomerados.
Exemplo:
Numa pesquisa consumo de certo produto, é mais fácil se ter a listagem
de bairros onde o produto é consumido do que de todos os consumidores
propriamente ditos. Então, sorteiam-se os bairros(conglomerados) e os
consumidores localizados nestes bairros formariam a amostra em um primeiro
estágio.
31

Exemplos de Conglomerados:
Quando se pretende pesquisar a avaliação de alunos de uma faculdade
quanto ao desempenho dos professores, pode-se considerar cada turma da
faculdade como um conglomerado e realizar o sorteio de certo número de
turmas, cujos alunos componentes constituirão amostra.
Em algumas situações, podemos identificar um grupo de elementos que
tenha aproximadamente a mesma composição da população. Neste caso pode
ser interessante realizar a amostragem somente com os elementos desse
grupo.
Outro Exemplo:
Algumas empresas, quando pretendem avaliar a aceitação de um
produto no eixo Rio- São Paulo, lançam o produto em Curitiba, cuja população
se comporta como uma miniatura do mercado eixo Rio- São Paulo.
32

Amostragens Não-probabilísticas:
São amostragens em que há uma escolha deliberada dos elementos da
amostra.
As amostras não-probabilísticas não asseguram naturalmente e
necessariamente que amostra gerada seja representativa da população, uma
vez que podem ter elementos da população que não tenham chance real de
fazerem parte da amostra . Isto coloca em discussão a sua confiabilidade.
As amostras não-probabilísticas são, muitas vezes, empregadas em
trabalhos estatísticos, por simplicidade ou por impossibilidade de se obterem
amostras probabilísticas como seria desejável. Como em muitos casos, os
efeitos da utilização de uma amostragem não-probabilísticas podem ser
considerados equivalentes aos de uma amostragem probabilística : os
processos não-probabilísticos de amostragem têm também sua importância.
Sua utilização, entretanto, deve ser feita com reservas e com a convicção de
que não introduzam tendências.
Tipos de Amostragens Não-Probabilísticas:
o Inacessibilidade a toda a população
o Amostragem a esmo ou sem norma
o População formada por material contínuo
o Amostragens intencionais
o Amostragens por voluntários
o Amostragem por quotas
Inacessibilidade a Toda a População
Esta situação ocorre com muita freqüência na prática.
Ocorre quando somos obrigados a colher a amostra na parte da
33

população que nos é acessível.
Surge, portanto, uma distinção entre população-objeto e população
amostrada. População-objeto é aquela que temos em mente ao realizar o
trabalho estatístico. População amostrada é aquela que está acessível para
que a amostra seja selecionada.
Se as características da variável de interesse forem às mesmas na
população-objeto e na população amostrada, então esse tipo de amostragem
equivalerá a uma probabilística. Uma situação muito comum em que ficamos
diante da inacessibilidade a toda a população é o caso em que parte da
população não tem existência real, isto é, é hipotética.
Exemplo:
Seja uma pesquisa em que a população alvo é constituída por todas as
peças produzidas por certa máquina. Mesmo estando à máquina em perfeito
funcionamento, existe uma parte da população que é formada por peças que
ainda vão ser produzidas.
Se nos interessa a população de todos os portadores de febre tifóide,
estaremos diante de um caso semelhante.
Em geral, estudos realizados com base nos elementos da população
amostrada terão, na verdade, seu interesse de aplicação voltado para os
elementos restantes da população-objeto. Esse fato realça a importância de se
estar convencido de que as duas populações podem ser consideradas como
tendo as mesmas características.
O presente caso de amostragem não-probabilística pode ocorrer
também quando, embora se tenha a possibilidade de atingir toda a população,
retiramos a amostra de uma parte que seja prontamente acessível.
34

Exemplo:
Se fôssemos recolher uma amostra de um monte de minério,
poderíamos por simplificação retirar a amostra de uma camada próxima da
superfície, pois o acesso as porções interiores seria problemático.
Amostragem a Esmo ou Sem Norma:
É a amostragem em que o amostrador, para simplificar o processo,
procura ser aleatório sem, no entanto, realizar propriamente o sorteio , usando
algum dispositivo aleatório confiável.
Exemplo:
Se desejarmos retirar uma amostra de 100 parafusos de uma caixa
contendo 10.000, evidentemente não faremos uma amostragem aleatória
simples, pois seria extremamente trabalhosa, mas procederemos à retirada
simplesmente a esmo.
Os resultados da amostragem a esmo são, em geral, equivalentes aos
de uma amostragem probabilística, se a população é homogênea e se não
existe a possibilidade de o amostrador ser inconscientemente influenciado por
alguma característica dos elementos da população.
População Formada por Material Contínuo:
Nesse caso, é impossível realizar amostragem probabilística devido à
impraticabilidade de um sorteio rigoroso: se a população for líquida ou gasosa.
O que se costuma a fazer é homogeneizar e retirar a amostra a esmo.
Tal procedimento pode, às vezes, ser usada no caso de material sólido.
Outro procedimento que pode ser empregada nesses casos,
especialmente quando a homogeneização não seja praticável, é a
35

enquartação, que consiste em subdividir a população em diversas partes (a
origem do nome pressupõe a divisão em quatro partes), sorteando-se uma ou
mais delas para constituir a amostra ou para delas retirar a amostra a esmo.
Amostragem Intencional:
Enquadram-se aqui os diversos casos em que o amostrador
deliberadamente escolhe certos elementos para pertencer à amostra, por julgar
tais elementos bem representativos da população.
Na amostragem intencional, o pesquisador simplesmente inclui os
sujeitos convenientes na amostra, dela excluindo os inconvenientes.
O perigo desse tipo de amostragem é obviamente grande, pois o
amostrador pode facilmente se equivocar em seu pré-julgamento. Apesar
disso, o uso de amostragens intencionais, ou parcialmente intencionais, é
bastante freqüente, ocorrendo em vários tipos de situações reais.
Exemplo:
O editor de uma “revista gay” pede aos seus leitores que respondam
perguntas sobre seu comportamento geral e opiniões para avaliar seu perfil e
estilo de vida.
Amostragem por Voluntários:
Ocorre quando o componente da população se oferece voluntariamente
para participar da amostra independente do julgamento do pesquisador.
Exemplo:
Ocorre, por exemplo, no caso da pesquisa experimental de uma nova
droga em que pacientes são solicitados, havendo concordância, a servirem de
36

“sujeitos” para a verificação da eficácia do novo medicamento. Os que se
interessarem se apresentarão voluntariamente ao pesquisador.
Amostragem por Quotas:
É a mais usada e conhecida amostragem não-probabilística. Muito
praticada no Brasil, sobretudo em pesquisas de mercado e de intenção de voto.
Na amostragem, por quota, diversas características de uma população,
tais como sexo, classe social ou etnia são amostradas nas mesmas proporções
em que figuram na população. Suponham, por exemplo, que tivéssemos de
extrair uma amostra, por quota, da população de alunos de uma dada
universidade, onde 42% fossem mulheres e 58% homens. Usando este
método, os entrevistadores recebem a incumbência de localizar uma quota de
estudantes de tal forma que somente 42% da amostra consista de mulheres e
58% de homens. As mesmas porcentagens que figuram na população são
reproduzidas na amostra. Se o tamanho global da amostra fosse 200, então 84
moças e 116 rapazes deveriam ser selecionados.
As amostras por quotas são usadas em certos tipos de pesquisa de
mercado e opinião pública, porém as inferências feitas nessas condições não
permitem a probabilidade do erro de amostragem.
Tamanho de Amostras para Estimação de Proporções Populacionais
em Pesquisas:
É o número mínimo de casos a ser amostrados, escolhidos
preferencialmente aleatoriamente, para garantir certa segurança estatística em
relação à representatividade dos dados na estimação de proporções em
pesquisas. O tamanho de uma amostra deve alcançar determinadas
dimensões mínimas, estabelecidas estatisticamente.
As necessidades práticas de tempo, custos, etc. Recomenda-se não
ultrapassar o tamanho mínimo determinado pela estatística.
37

Portanto, é necessário conhecer a forma de calcular o tamanho da
amostra, não só para garantir a possibilidade de generalizar os resultados, mas
também pelos aspectos práticos mencionados.
O tamanho da amostra depende dos seguintes fatores:
o Tamanho da população do universo
o Nível de confiança estabelecido
o Erro de amostragem permitido
o Proporção de uma quota característica importante do universo
População Finita e População Infinita
Segundo o tamanho da população, o universo divide-se em finito e
infinito. Consideram-se universos finitos(limitados) aqueles que não
ultrapassam às 100.000 unidades(pessoas, alunos, estabelecimentos
educacionais, empresas, países etc.). Universos infinitos são aqueles que
ultrapassam essa quantidade. Tal distinção é importante para determinar o
tamanho da amostra, pois as fórmulas são diferentes. No caso do universo
infinito, supõe-se que o seu tamanho da população não influi na fórmula a
aplicar. O universo finito depende do número de unidades da população. Neste
curso, apresentam-se as fórmulas mais simples, para amostras aleatórias
simples e amostras estratificadas.
38

Tamanho de Amostras em Amostragem Aleatória Simples:
Exemplo 1:
Numa pesquisa sobre as atitudes dos estudantes das universidades
paulistas em relação às suas expectativas sexuais pré-matrimoniais, qual é o
tamanho de uma amostra representativa, com um nível de confiança de 99% e
um erro permitido de 4%?
Convém utilizar a fórmula para universos infinitos, pois as universidades
de São Paulo têm mais de 100.000 alunos. Portanto, o tamanho da população
não influi no cálculo desta amostra.
n = (Z2
. P . Q)/E2
Onde:
n = tamanho da amostra
Z = escore da curva normal que é função do nível de confiança
escolhido.
Na tabela abaixo, apresentamos valores de Z, retirados da curva normal,
em função do nível de confiança arbitrado:
Confiança (%) Z
68 1,00
90 1,65
95 2,00
99 3,00
O objetivo do pesquisador é estimar a proporção populacional π. Como
se não conhece π, deve-se obter uma amostra piloto( n´ ) e nela estimar π pela
freqüência relativa amostral P.
39

Se n < n´ → a amostra piloto já foi suficiente.
Portanto:
P é a estimativa de uma proporção populacional de interesse( que se
quer estimar) obtida numa amostra piloto de n´ elementos. Se concluir-se que n
< n´, a amostra piloto já terá sido suficiente para a estimação da proporção de
interesse P.
Quando não se dispuser da estimativa de P, pode-se supor que ela seja
50% na população, o caso mais desfavorável na estimação, pois é aquela em
que se trabalha com o tamanho máximo de amostra. É lógico, se a estimativa
da proporção da característica pesquisada fosse outro, seria necessário um
menor número de casos.
Q = 100 – P.
Exemplo: A proporção P de alfabetizados na amostra piloto é igual a
40%, tem-se Q = 100- 40 = 60%
.
E = erro de amostragem, em termos percentuais, definido da seguinte
forma:
E = | π - P | ,
Onde:
π = proporção de uma característica populacional que se deseja estimar
P = estimativa da proporção π obtida junto a uma amostra piloto
No exemplo:
40

Para uma confiança de 99%, Z = 3
n = (32
. 50 . 50) / 42
= 1406,25 = 1406 estudantes.
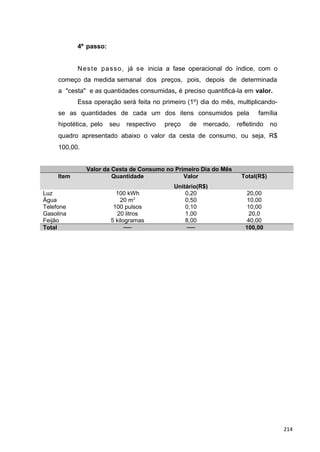
Assim, o resultado obtido significa que o tamanho da amostra deve ser
pelo menos 1406 estudantes, para oferecer segurança de probabilidade de
99% de resultados válidos para o universo e de 4% de erro admitido.
Exemplo 2:
Suponha-se que a pesquisa sobre as atitudes dos estudantes
universitários seja realizada na Paraíba, onde os resultados não passam de
50.000. Além disso, o pesquisador quer trabalhar apenas com um nível de
confiança de 95% e um erro de amostragem de 4%. Qual é o tamanho da
amostra, com essas exigências? Considerando que o universo é menor que
100.000 estudantes, utiliza-se a fórmula para universos finitos:
n = [Z2
. P . Q . N] / [E2
. (N – 1) + Z2
. P .Q]
Onde N é o tamanho da população.
Cálculo:
Para uma confiança de 95%, Z = 2
n = [22
. 50 . 50 . 50.000] / [16 . (50.000 – 1) + 22
. 50 .50] = 617,3 = 617
estudantes.
41

Exemplo 3:
Numa pesquisa de mercado bem conduzida, 57 das 150 pessoas
entrevistadas afirmaram que seriam compradoras de certo produto a ser
lançado. Essa amostra é suficiente para estimar a proporção real de futuros
compradores, com uma precisão de 0,08 e confiança de 95%?
Tem-se P= 57/150 = 0,38
22
. 0,38.0,62
n = ──────────── = 0,9424 / 0,0064 = 147 pessoas
( 0,08)2
Como n´= 150 > n=147, conclui-se que a amostra piloto é suficiente.
Exemplo 4:
Qual o tamanho da amostra suficiente para se estimar a proporção de
defeituosas fornecida por uma máquina, com precisão de 0,02 e 95% de
confiança, sabendo que essa proporção seguramente não é superior a 20%?
22
. 0,20.0,80
n = ──────────── = 0,64 / 0,0004 = 1600 elementos
( 0,02)2
42

Cálculo do Tamanho da Amostra Alternativo:
1
n0 = ──────
E2
N. n0
n = ──────
N+n0
Onde:
N = tamanho da população
E = erro amostral tolerável
n0 = primeira aproximação do tamanho da amostra
n = tamanho da amostra
Exemplo 1:
Num estudo sobre pesquisa de orçamento familiar, temos N =
200 famílias e E = erro amostral tolerável = 4% (E = 0,04)
n0 = 1/(0,04)2
= 625 famílias
n (tamanho da amostra corrigido) =
n = 200x625/200+625 = 125000/825 = 152 famílias
E se a população fosse de 200.000 famílias?
n = (200.000)x625/(200.000 +625) = 623 famílias
43

Observação:
Observe=se que se N é muito grande, não é necessário
considerar o tamanho exato N da população. Nesse caso, o
cálculo da primeira aproximação já é suficiente para o cálculo:
1
n = n0 = ──────
E2
O tamanho da amostra deve ser tomado como um percentual
do tamanho da população?
Observe que: N = 200 famílias, E0 = 4%
n = 152 famílias →76% da população
Observe que: N = 200.000 famílias, E0 = 4%
n = 623 famílias → 0,3% da população
Logo, é errôneo pensar que o tamanho da amostra deve ser
tomado como um percentual do tamanho da população para ser
representativa.
O cálculo do tamanho de amostra que acabamos de estudar
independe do nível de confiança e do valor da proporção P. Quando
usamos este recurso estamos adotando sempre um nível de
confiança de 95% e a proporção P= 50%.
44

Tamanho de Amostras em Amostragem Estratificada ou por
Quotas:
As amostras estratificadas apresentam um problema especial
na determinação de seu tamanho. O número de casos de amostra
global pode ser calculado utilizando-se fórmulas já analisadas, mas
deve-se, também, calcular o tamanho de cada estrato dos grupos. É
a condição básica desse tipo de amostra que deve representar, o
mais exatamente possível, os estratos, segundo sua proporção na
população. A forma mais simples de calcular o tamanho da amostra,
as respectivas percentagens que cada estrato representa na
população. Isso permite determinar o número de casos a ser
distribuído em cada um deles.
Exemplo 1:
Um pesquisador realiza um estudo sobre a imagem que
empresários americanos têm das condições políticas e
econômicas de uma cidade que pretendem expandir seus
negócios. De acordo com as informações em poder do
pesquisador, esse tipo de comportamento varia muito de
acordo com a área dos empresários. Portanto, o pesquisador
está interessado em levantar tal imagem estratificando os
empresários por área de atuação. Na época da pesquisa a
cidade alvo da expansão tinha 10.000 empresários, o nível de
confiança corresponde a 95% e o erro de amostragem
permitido é de 4%. De acordo com a informação disponível, os
empresários distribuem-se nas seguintes áreas:
45

Base da Amostra:
Áreas Estratos Populacionais
Construção Civil 1000
Financeira 2000
Alimentação 3000
Comércio 4000
Total 10.000
1o
) Determinação do tamanho proporcional dos estratos:
Áreas Cálculos Estratos Amostrais
Construção Civil 1000/10000 10%
Financeira 2000/10000 20%
Alimentação 3000/10000 30%
Comércio 4000/10000 40%
Total ─── 100%
2o
) Tamanho Global da amostra:
n = [22
. 50 . 50 . 10.000] / [16 . (9.999) + 22
. 50 .50] = 588
46

3o
) Número de casos em cada estrato amostral:
Áreas Cálculos Estratos Amostrais
Construção Civil 10% de 588 59
Financeira 20% de 588 118
Alimentação 30% de 588 176
Comércio 40% de 588 235
Total ─── 588
Exemplo 2:
Analistas de um site de relacionamento estão planejando
realizar uma pesquisa junto aos seus clientes para descobrir suas
expectativas futuras para o amor. A pesquisa envolverá uma
amostra por quota de clientes que estejam on line durante um
período de 3 meses. Os analistas acreditam que aspectos como
gênero, estado-civil, aparência e faixa-etária sejam essências para
manter a representatividade da amostra e assegurar a precisão das
estimativas. A pesquisa terá 5% de erro de amostragem para mais
ou para menos. Informações prévias do perfil da população quanto
às variáveis importantes para a representatividade se encontra
abaixo:
Sexo: masculino e feminino
Estado-civil: solteiro, casado, viúvo e divorciado
Aparência: boa aparência e má aparência
Faixa-etária: jovem, adulto e idoso
47

Dados Populacionais com os Números Absolutos Referentes às
Variáveis Escolhidas
Categorias População
Masculino solteiro boa aparência jovem 340
Masculino solteiro boa aparência adulto 445
Masculino solteiro boa aparência idoso 175
Masculino solteiro má aparência jovem 310
Masculino solteiro má aparência adulto 470
Masculino solteiro má aparência idoso 150
Masculino casado boa aparência jovem 100
Masculino casado boa aparência adulto 115
Masculino casado boa aparência idoso 65
Masculino casado má aparência jovem 160
Masculino casado má aparência adulto 200
Masculino casado má aparência idoso 250
Masculino viúvo boa aparência jovem 260
Masculino viúvo boa aparência adulto 295
Masculino viúvo boa aparência idoso 90
Masculino viúvo má aparência jovem 150
Masculino viúvo má aparência adulto 175
Masculino viúvo má aparência idoso 135
Masculino divorciado boa aparência jovem 335
Masculino divorciado boa aparência adulto 340
Masculino divorciado boa aparência idoso 115
Masculino divorciado má aparência jovem 500
Masculino divorciado má aparência adulto 525
Masculino divorciado má aparência idoso 300
48

Continuação....
Categorias População
Feminino solteiro boa aparência jovem 350
Feminino solteiro boa aparência adulto 395
Feminino solteiro boa aparência idoso 75
Feminino solteiro má aparência jovem 410
Feminino solteiro má aparência adulto 52
Feminino solteiro má aparência idoso 200
Feminino casado boa aparência jovem 100
Feminino casado boa aparência adulto 52
Feminino casado boa aparência idoso 65
Feminino casado má aparência jovem 160
Feminino casado má aparência adulto 46
Feminino casado má aparência idoso 250
Feminino viúvo boa aparência jovem 300
Feminino viúvo boa aparência adulto 400
Feminino viúvo boa aparência idoso 295
Feminino viúvo má aparência jovem 140
Feminino viúvo má aparência adulto 175
Feminino viúvo má aparência idoso 140
Feminino divorciado boa aparência jovem 335
Feminino divorciado boa aparência adulto 350
Feminino divorciado boa aparência idoso 310
Feminino divorciado má aparência jovem 650
Feminino divorciado má aparência adulto 450
Feminino divorciado má aparência idoso 300
Total 12000
Realize o “desenho de uma amostra por quotas”
Cálculo das Proporções das Variáveis para a População
49

Categorias %
Masculino solteiro boa aparência jovem 2,8
Masculino solteiro boa aparência adulto 3,7
Masculino solteiro boa aparência idoso 1,5
Masculino solteiro má aparência jovem 2,6
Masculino solteiro má aparência adulto 3,9
Masculino solteiro má aparência idoso 1,3
Masculino casado boa aparência jovem 0,8
Masculino casado boa aparência adulto 1,0
Masculino casado boa aparência idoso 0,5
Masculino casado má aparência jovem 1,3
Masculino casado má aparência adulto 1,7
Masculino casado má aparência idoso 2,1
Masculino viúvo boa aparência jovem 2,2
Masculino viúvo boa aparência adulto 2,5
Masculino viúvo boa aparência idoso 0,8
Masculino viúvo má aparência jovem 1,3
Masculino viúvo má aparência adulto 1,5
Masculino viúvo má aparência idoso 1,1
Masculino divorciado boa aparência jovem 2,8
Masculino divorciado boa aparência adulto 2,8
Masculino divorciado boa aparência idoso 1,0
Masculino divorciado má aparência jovem 4,2
Masculino divorciado má aparência adulto 4,4
Masculino divorciado má aparência idoso 2,5
50

Continuação....
Categorias %
Feminino solteiro boa aparência jovem 2,9
Feminino solteiro boa aparência adulto 3,3
Feminino solteiro boa aparência idoso 0,6
Feminino solteiro má aparência jovem 3,4
Feminino solteiro má aparência adulto 0,4
Feminino solteiro má aparência idoso 1,7
Feminino casado boa aparência jovem 0,8
Feminino casado boa aparência adulto 0,4
Feminino casado boa aparência idoso 0,5
Feminino casado má aparência jovem 1,3
Feminino casado má aparência adulto 0,4
Feminino casado má aparência idoso 2,1
Feminino viúvo boa aparência jovem 2,5
Feminino viúvo boa aparência adulto 3,3
Feminino viúvo boa aparência idoso 2,5
Feminino viúvo má aparência jovem 1,2
Feminino viúvo má aparência adulto 1,5
Feminino viúvo má aparência idoso 1,2
Feminino divorciado boa aparência jovem 2,8
Feminino divorciado boa aparência adulto 2,9
Feminino divorciado boa aparência idoso 2,6
Feminino divorciado má aparência jovem 5,4
Feminino divorciado má aparência adulto 3,8
Feminino divorciado má aparência idoso 2,5
Total 100
51

Cálculo do Tamanho da Amostra
Exemplo:
N = 12000 clientes
e = erro amostral tolerável = 5% (e = 0,05)
n0 = 1/(0,05)2
= 400
n = 12000x400/12000+400 = 4.800.000/12.400 = 387
clientes
A primeira aproximação do tamanho da amostra já é
suficiente.
52

Número de Entrevistas por Quotas
Categorias Amostra
Masculino solteiro boa aparência jovem 11
Masculino solteiro boa aparência adulto 15
Masculino solteiro boa aparência idoso 6
Masculino solteiro má aparência jovem 10
Masculino solteiro má aparência adulto 16
Masculino solteiro má aparência idoso 5
Masculino casado boa aparência jovem 3
Masculino casado boa aparência adulto 4
Masculino casado boa aparência idoso 2
Masculino casado má aparência jovem 5
Masculino casado má aparência adulto 7
Masculino casado má aparência idoso 8
Masculino viúvo boa aparência jovem 9
Masculino viúvo boa aparência adulto 10
Masculino viúvo boa aparência idoso 3
Masculino viúvo má aparência jovem 5
Masculino viúvo má aparência adulto 6
Masculino viúvo má aparência idoso 5
Masculino divorciado boa aparência jovem 11
Masculino divorciado boa aparência adulto 11
Masculino divorciado boa aparência idoso 4
Masculino divorciado má aparência jovem 17
Masculino divorciado má aparência adulto 18
Masculino divorciado má aparência idoso 10
53

Continuação....
Categorias Amostra
Feminino solteiro boa aparência jovem 12
Feminino solteiro boa aparência adulto 13
Feminino solteiro boa aparência idoso 3
Feminino solteiro má aparência jovem 14
Feminino solteiro má aparência adulto 2
Feminino solteiro má aparência idoso 7
Feminino casado boa aparência jovem 3
Feminino casado boa aparência adulto 2
Feminino casado boa aparência idoso 2
Feminino casado má aparência jovem 5
Feminino casado má aparência adulto 2
Feminino casado má aparência idoso 8
Feminino viúvo boa aparência jovem 10
Feminino viúvo boa aparência adulto 13
Feminino viúvo boa aparência idoso 10
Feminino viúvo má aparência jovem 5
Feminino viúvo má aparência adulto 6
Feminino viúvo má aparência idoso 5
Feminino divorciado boa aparência jovem 11
Feminino divorciado boa aparência adulto 12
Feminino divorciado boa aparência idoso 10
Feminino divorciado má aparência jovem 22
Feminino divorciado má aparência adulto 15
Feminino divorciado má aparência idoso 10
Total 400
54

Amostragem por Quotas versus Amostragem Aleatória Estratificada
1a
) Amostragem por Quotas:
Passos:
• Definir as variáveis relevantes para o estudo planejado;
• Obter os dados censitários com os números absolutos referentes
às variáveis escolhidas;
• Calcular as proporções das variáveis para a população;
• Definir o tamanho da amostra;
• Multiplicar as proporções de cada variável obtida ou o cruzamento
destas pelo tamanho da amostra;
• Localizar os respondentes de cada quota em ruas, em locais
ou pontos de grande movimento.
2a
) Amostragem Aleatória Estratificada:
Passos:
• Definir as variáveis relevantes para o estudo planejado;
• Obter os dados censitários com os números absolutos referentes
às variáveis escolhidas;
• Calcular as proporções das variáveis para a população;
• Definir o tamanho da amostra;
• Multiplicar as proporções de cada variável obtida ou o cruzamento
destas pelo tamanho da amostra;
55

• Localizar os respondentes de cada estrato amostral através
da realização de uma amostragem aleatória simples em cada
estrato populacional.
Comparações:
• As amostras por quotas são mais simples que as estratificadas,
de tecnologia mais fácil e são bem mais baratas;
• As amostras estratificadas têm sustentação teórica e empírica;
• A amostra por quota somente tem sustentação empírica.
56

1) Responda às questões abaixo:
a) Explique o que você entende por população e amostra
b) O que você entende por amostragem?
c) Qual a função da tecnologia da amostragem?
d) Qual o melhor tipo de amostragem para uma pesquisa em particular?
e) Qual a justificativa para se utilizar amostragem?
f) Quais os tipos de amostragem existentes?
g) Qual a diferença entre conglomerados e estratos?
h) O que é amostragem probabilística?
i) O que é erro de amostragem?
j)O que é intervalo de confiança?
k) O que é precisão?
l)O que é tamanho da amostra?
m)Quais os tipos de amostragem probabilística?
n) Defina e explique amostragem aleatória simples.
o)Qual o dispositivo prático para se selecionar aleatoriamente uma
amostra?
p) Qual a diferença básica entre amostragem probabilística e não
probabilística?
q) Explique a amostragem por quotas?
r) Em que tipo de amostragem o tamanho da amostra é dimensionado
matematicamente?
s) Que tipo de amostragem é considerado a única científica? Por quê?
t) Qual tipo de amostragem probabilística em que não é preciso um
cadastro ou listagem de toda a população para se realizar a seleção da
amostra? Por quê?
u) Quais os dois elementos que devem ser estabelecidos a priori ao se
determinar o tamanho da amostra?
57

v) O que é nível de significância na determinação do tamanho da
amostra?
w) O que é precisão na determinação do tamanho da amostra?
2) Um instituto de pesquisa vai realizar uma pesquisa de opinião de
intenção de voto por amostragem por cotas.
A base da amostra foi obtida junto ao IBGE e está apresentada na tabela
abaixo:
Sexo Faixas de Idades (em anos)
0 a 20 21 a 40 41 anos ou mais Total
Masculino 120 205 125 450
Feminino 180 255 185 620
Total 300 460 310 1070
Realize o ‘desenho’ da amostra para o instituto, desenvolvendo os
passos abaixo:
 Elabore a tabela com as cotas populacionais que devem ser
guardadas na amostra;
 Determine o tamanho da amostra ou o número de entrevistas a
serem realizadas para uma margem de erro de 10%, para mais
ou para menos, com uma confiança de 95%. Considere P=50%.
 Determine a tabela com o número de entrevistas por cotas.
Fórmula:
n = Z2
. P .Q
e2
58

3)Para levantar dados sobre o número de filhos por casal, em uma
comunidade, um pesquisador organizou um questionário que enviou, pelo
correio, a certo número de residências amostradas aleatoriamente. A
resposta ao questionário era facultativa, pois o pesquisador não tinha
condições de exigir resposta. Neste questionário pergunta-se o número
de filhos por casal morador na residência. Você acha que os dados assim
obtidos têm algum tipo de tendenciosidade?
4)Um pesquisador pretende levantar dados sobre o número de moradores
por domicílio, usando a técnica da amostragem sistemática. Para isso, o
pesquisador sorteará uma primeira residência dentro do intervalo de
amostragem, a partir daí visitará as casas em cinco em cinco numa
progressão aritmética. Se nenhuma pessoa estiver presente na ocasião
da visita, o pesquisador excluirá o domicílio da amostra e visitará a quinta
residência próxima até formar o tamanho da amostra. Esta última
determinação introduz tendenciosidade? Por quê?
5)Muitas pessoas acreditam que as famílias se tornaram menores.
Suponha que, para estudar essa questão, foi selecionada uma amostra
aleatória de 2000 casais com filhos e perguntou-se quantos filhos eles
tinham, quantos filhos tinham seus pais e quantos filhos tinham seus
avós. O procedimento introduz tendenciosidade nos dados? Por quê?
6)Qual o tamanho da amostra para estimar a proporção de pessoas do
sexo masculino no Rio de Janeiro com erro de amostragem de 1% e
confiança de 95%?
59

7) Os dados abaixo referem à população hipotética de certa cidade com
presença ou não de telefone:
N S N S S N N S N N
N N N N S N S S S N
N S N S S N N S N N
N N N N S N S S S N
N S N S N N N S N N
N N N N S N S S S N
N S N S S N N S N N
N N N N S N S S S N
S S S S S N N S N N
N N N N S N S S S N
S S N S S N N S N N
N N N N S N S S S N
N S N S S S N S N N
N N S N S N S S S N
S S N S S N N S N N
N N N N S N S N S N
N S N S N N N S N N
S N N N S N S S N N
N S N S S N N S N
S N N S N S S S N
S S S S S S N N S N N
N N N N S N S S S S N
S S N S S N N S N N
S N N N N N S N S N
N S S S S N N S N N
N N N N S N S N N N
S N N S S N N S N N
N N N N S N S S S S N
S N N N S N N S S N
60

Onde S, significa presença de telefone e N, a pessoa não tem telefone.
Faça o que se pede:
a) Selecione através da planilha eletrônica Excel uma amostra aleatória
simples de tamanho 100.
b) Calcule a porcentagem de pessoas com telefone. O que significam
estas medidas?
8)Um administrador financeiro está interessado em descobrir o percentual
de famílias com problemas de dívida. Para isso irá realizar uma
investigação nas residências das pessoas do bairro sob investigação. O
bairro em estudo tem 10 ruas descritas abaixo, segundo residência e
existência de dívidas ( S = sim e N = não):
Rua A : S S S S S S S N
Rua B : S S N S N S N S S S S N
Rua C : N S N S N S S N S N S
Rua D : S S S N N S S N N S
Rua E : S S N N S S
Rua F: S N N S S
Rua G : S N S S N S N N N S S N N S S N N
Rua H : S N N S S N S N S N S
Rua I : S N N S
Rua J : S S S NN S S S N S N S S N N S S
Selecione uma amostra por conglomerados por bairro de tamanho 5,
utilizando a planilha eletrônica Excel.
61

9) Os dados abaixo se referem ao consumo, em mil reais, de um produto
comercializado por uma loja:
130,0 105,0 120,0 111,5 99,0 116,0 82,5
107,5 125,0 100,0 107,5 120,0 143,0 115,0
135,0 130,0 135,0 127,5 90,5 104,5 136,5
100,0 145,0 125,0 104,5 101,5 90,5 101,5
134,5 158,5 110,0 102,5 90,5 115,5 124,5
121,5 135,0 102,0 119,5 115,5 125,5 117,5
107,5 140,0 121,5 107,5 113,3 93,0 103,5
Selecione uma amostra aleatória de tamanho 10, com base em funções
do Excel e:
a) Calcule a média populacional;
b) Calcule a média amostral;
c) Calcule o erro de amostragem em módulo.
10)Numa empresa com 1000 funcionários, deseja-se estimar a
percentagem dos favoráveis a certo treinamento. Qual deve ser o
tamanho da amostra aleatória simples que garanta um erro amostral não
superior a 5%?
11)Com o objetivo de avaliar a confiabilidade de um novo sistema de
transmissão de dados, torna-se necessário verificar a proporção de bits
transmitidos com erro em cada lote de 100Mb. Considere que seja
necessário um erro amostral máximo de 2%. Qual deve ser o tamanho da
amostra?
62

12)Sabe-se que no Brasil 2.883 municípios têm cobertura banda larga 3G,
dados de fevereiro de 2012. Qual o tamanho da amostra necessário para
estimar o percentual de municípios com cobertura banda larga 3G da
operadora Claro, com um erro de amostragem de ±4%?
13))Numa pesquisa para uma eleição presidencial, qual deve ser o tamanho de
uma amostra aleatória simples, se deseja garantir um erro amostral não superior
a 2%?
14)Em 2011, 2176 instituições de ensino superior no Brasil participaram do
ENADE. Qual o tamanho da amostra necessário para se estimar a proporção de
centros universitários e universidades com IGC 1 e 2, com 95% de confiança de
que o erro efetivo de amostragem não ultrapasse o tolerado que é de ±5%?
15)Qual o tamanho da amostra para se estimar a nota média de alunos no
vestibular de uma faculdade, onde a variação das notas não passa de 400 e
admitindo uma confiança de 95% e um erro de amostragem de ±2 pontos?
63

Unidade IV
Fases do Método Estatístico
Método:
É um conjunto de etapas, ordenadamente dispostas, a serem seguidas
na investigação da verdade, no estudo de uma ciência ou para alcançar
determinado fim.
Método Estatístico:
É um conjunto de fases, que devem ser seguidas na ordem
determinada, para se obter resultados estatísticos.
Fases do Método Estatístico:
Com essa ou outra nomenclatura, com menos ou mais detalhes, a
literatura sobre o assunto admite tais fases do trabalho estatístico:
o Planejamento:
o Coleta de Dados;
o Crítica de Dados;
o Apuração de Dados;
o Análise de Dados;
o Emissão do Relatório Final;
o Comunicação dos Resultados.
64

Planejamento
Na fase de planejamento, podemos resumir em uma lista,
como a que segue, as principais etapas a serem desenvolvidas no
planejamento:
1. Definir o objetivo ou problema da pesquisa;
2. Definir a necessidade(relevância) da pesquisa;
3. Definir as variáveis da pesquisa;
4. Definir a necessidade da pesquisa com trabalho
de campo e as fontes dos dados da pesquisa;
5. Identificar o esquema de amostragem (como
escolher a amostra e que tamanho essa amostra
deve ter);
6. Decidir que método de coleta de dados será
utilizado (questionário via e-mail, impresso auto-
aplicável, entrevista, telefone, etc.)
7. Definir materiais e métodos da pesquisa;
8. Selecionar e treinar qualquer pessoa envolvida no
processo de coleta de dados
9. Definir o orçamento da pesquisa;
10.Definir o cronograma da pesquisa.
Deste modo, o trabalho estatístico nasce quando um
estudioso (pesquisador) sente a curiosidade de conhecer com mais
precisão o comportamento de um fenômeno coletivo ou de massa.
Esta curiosidade estatística é o objetivo ou problema de pesquisa.
65

Exemplo:
Um economista deseja conhecer quais as características
demográficas, socioeconômicas e de estilo de vida dos
consumidores de certo bem ou serviço.
Necessidade(relevância) da Pesquisa
Considerando os volumes relativos de investimentos que o
mercado exige para realização adequada de produtos e serviços,
supérfluo seria discutir a sua importância. A pesquisa já há tempo
vem sendo uma rotina nas empresas e institutos mais avançados e
já se desenvolve em pequenas e médias corporações e instituições.
Ninguém quer se arriscar a investir amadoristicamente, com base
apenas em suposições. Ninguém quer “queimar” o seu serviço
colocando-o inadequadamente no mercado. Ao saber que os bancos
públicos reduzirão fortemente as taxas de juros para empréstimos e
financiamentos, empresários devem buscar informações balizadas
do impacto dessa decisão no consumo de seus bens e serviços
colocados no varejo.
O que importa, de fato, não é discutir a necessidade da
pesquisa, porque isso é uma fato hoje incontestável. O relevante é
discutir o momento certo para viabilizá-la e que tipo de dados é mais
viável economicamente.
66

Exemplo:
Num estudo do “Perfil dos turistas envolvidos em um
pacote viagem em uma cidade”, a motivação para a pesquisa
poderá ser o de obter informações para que no futuro se aperfeiçoe
o oferecimento do referido pacote turístico cada vez mais moldado
ao perfil e à necessidade de quem o demanda.
Definição das Variáveis da Pesquisa
O pesquisador precisa definir quais as características ou
variáveis precisam ser observadas para responderem ao seu
objetivo de pesquisa.
Exemplo:
Para conhecer as características demográficas,
socioeconômicas e de estilo de vida de consumidores de um serviço
bancário, é necessário observarmos dentre outras, o sexo, idade,
estado-civil, renda, análise de crédito, etc.
67

Definição da Necessidade da Pesquisa com Trabalho de Campo
Para verificar a necessidade e momento certo de um trabalho de
pesquisa efetivo, com coleta de dados, devemos responder as
seguintes perguntas:
a) Que informações são necessárias para responder ao
meu problema de pesquisa?
b) Estas informações estão disponíveis e são suficientes
para resolver o meu problema de pesquisa no
momento?
c) Podem ser consultadas em tempo hábil na empresa ou
em outras partes?
d) Se as soluções às ultimas perguntas forem negativas
está estabelecida à necessidade de pesquisa com
trabalho de campo.
Então, podemos concluir que a pesquisa com trabalho de
campo aparece nitidamente como necessidade, quando trabalhadas
e analisadas as informações já disponíveis ao pesquisador, este
observa que ainda resta um vazio, que algumas questões ainda não
ficam respondidas, algumas dúvidas não se resolvem. A
insuficiência de dados disponíveis é o fundamento que se precisa
para a pesquisa com trabalho de campo.
68

Projeto de Pesquisa:
Quando tudo for estabelecido, resume-se o que se planejou
em um pequeno relatório escrito que se chama “Projeto de
Pesquisa”, com o problema de pesquisa, metodologias, prazos,
orçamentos, etc. e submeta às autoridades da empresa ou outra
fonte de aprovação da realização da mesma.
Coleta de Dados ( Trabalho de Campo )
É a observação, o registro ou a medição sistemática da
manifestação das variáveis de pesquisa.
Para a coleta de dados são mais utilizados os métodos de
questionários, realização de entrevista ou a consecução de
observação. É a parte visível da pesquisa, é o entrevistador
abordando os entrevistados em uma rua de grande movimento, ou
em suas residências, locais de trabalho, locais de estudo, para
colher dados sobre as variáveis da pesquisa.
Em pesquisas de mercado, pesquisas eleitorais, pesquisas de
opinião, pesquisas de intenção de votos, são comuns se localizarem
os respondentes (ou entrevistados) em locais ou pontos de grande
movimento ou ruas.
69

Fontes de Dados
Há quatro diferentes fontes de dados em pesquisa:
a) Pesquisado;
b) Pessoas que tenham informações sobre o pesquisado;
c) Situações similares;
d) Dados disponíveis.
Pesquisado
Os próprios pesquisados são a maior fonte de dados em
pesquisa. O dado pode ser obtido do pesquisado através de sua
própria declaração, oralmente ou por escrito, ou através de sua
observação.
Exemplo:
Numa pesquisa de “Clima Organizacional”, as entrevistas
realizadas junto aos funcionários da empresa é um exemplo de
pesquisa cuja fonte dos dados é o próprio pesquisado.
70

Pessoas que tenham informações sobre o pesquisado
Quando ocorre de o pesquisado ser inacessível, possuir
pouco conhecimento da informação desejada ou tiver dificuldade de
expressar-se, às vezes, é mais fácil conseguir a informação com
outras pessoas que tenha informações confiáveis sobre ele.
Exemplos:
⇒ Obter informações sobre as crianças de uma casa com a
mãe;
⇒ Obter informação sobre o marido com a esposa;
⇒ Obter informação sobre o chefe com a secretaria;
⇒ Obter informação sobre o subordinado com o chefe;
⇒ Obter informação sobre o cliente com o vendedor.
Situações Similares
É a busca de conhecimento em situações análogas ou
similares.
Exemplos:
⇒ Aprende-se bastante em saber como lançar no mercado, para
posterior venda, um bem ou serviço, através do mesmo
procedimento já vivido por outras empresas;
⇒ Como outras empresas do mesmo ramo trabalham com a
variável promoção de vendas;
⇒ Como foram as reações dos consumidores quando
determinada marca de carros foi lançada em outro país de
71

mesma cultura e desenvolvimento econômico.
Dados Disponíveis
Existe uma infinidade de dados úteis para o analista que já
foram coletados, tabulados e, às vezes, até analisados que estão
catalogados à disposição dos interessados.
Para obter estes dados exige-se apenas o esforço de dedicar
algum tempo à consulta de órgãos de geração de informações para
o turismo e no mundo atual, a pesquisa na internet.
Existe uma infinidade de informações sobre turismo já
disponíveis.
Tipos de Dados
Dados Primários
Dados primários são aqueles que ainda não passaram pelas
fases da apuração e análise de dados. São aqueles que ainda não
foram trabalhados estatisticamente.
Exemplo:
Numa pesquisa de “Satisfação de clientes” ou de “Clima
Organizacional”, após a aplicação dos questionários ou da
realização das entrevistas, temos ainda dados primários.
As fontes básicas de dados primários seriam:
⇒ Pesquisado;
⇒ Pessoas que tenham informações sobre o pesquisado;
⇒ Situações Similares.
72

Dados Secundários
São aqueles que já passaram pelas fases da apuração e da
análise de dados, e já estão à disposição para interpretação e
tomadas de decisão, ou até mesmo para serem “retrabalhados“
estatisticamente.
Exemplos:
o As estatísticas fornecidas nos relatórios técnicos do
Instituto de Economia Aplicada(IPEA) são dados
secundários;
o As pesquisas de intenção de votos divulgadas à mídia
e a candidatos são dados secundários;
o Os índices de audiências fornecidos às emissoras de
TV são dados secundários.
o O Anuário Estatístico do IBGE contém para consulta
dados secundários.
As fontes básicas de dados secundários são:
⇒ A própria empresa.
⇒ Publicações.
⇒ Governos.
⇒ Instituições não governamentais.
⇒ Serviço padronizado de informações em marketing.
⇒ Internet.
74

Seqüência na Procura de Dados em Pesquisas no Turismo:
É comum as pessoas imaginarem que a única forma de obter
dados em pesquisa de negócios seja através de um levantamento
de campo. Na verdade, os levantamentos de campo e outras formas
de coleta de dados primários somente deverão ser usados se outras
formas mais rápidas, baratas e eficientes não conseguirem atender
às necessidades de dados da pesquisa.
Um grande esforço nos estágios iniciais da pesquisa deverá
ser canalizado para procurar tentar descobrir se, ao menos em
parte, os dados necessários estejam de alguma forma disponíveis.
Este esforço inicial poderá significar grande economia de
tempo, dinheiro e energia na realização da pesquisa.
É apresentada na tabela abaixo, a seqüência dos passos no
processo, que normalmente deve ser seguida na definição dos
dados e das fontes de dados no processo de pesquisa estatística.
75

Tabela
Etapas para Definição dos Dados e das Fontes de Dados no Processo de
Pesquisa Estatística
1. Definir os objetivos da pesquisa.
2. Especificar as necessidades de dados.
3. Planejar as etapas da pesquisa.
4. Determinar as fontes de dados.
5. Procurar dados secundários internos.
6. Procurar dados secundários externos:
Publicações:
- gerais
- governamentais
- institucionais
Governos:
- federal
- estadual
- municipal
Instituições não governamentais:
- universidades, faculdades e centros de pesquisas
- associações patronais e de empregados
- sindicatos patronais e de empregados
Serviços padronizados de informações de marketing:
7. Determinação das necessidades de dados primários.
76

Determinação das fontes de dados primários:
- pesquisado
- pessoas que tenham informações sobre o pesquisado
- situações similares:
• estudo de casos
• experimentos
Crítica de Dados:
É a preparação dos dados coletados para a apuração. Constitui a
verificação de respostas erradas, verificação de lacunas deixadas pelos
informantes e quantificação de perdas naturais de informações.
Apuração de Dados:
É a contagem ou soma dos resultados observados de cada variável
especificada e medida no questionário.
Exemplo de Apuração:
Suponha que na pesquisa do “Perfil dos Clientes da Clínica”, uma
variável observada seja ‘sexo dos clientes’ e que do resultado da coleta a 10
clientes tivéssemos encontrado:
Indivíduo 1: Masculino,
Indivíduo 2: Feminino,
77

Indivíduo 9: Feminino
Indivíduo 10: Masculino.
Este tipo de apuração é a Manual. A apuração de dados é a contagem
dos dados registrados, no caso do exemplo, de quantas pessoas do sexo
masculino e do sexo feminino foram observadas.
Geralmente o número de observados é bem maior do que 10, então a
apuração se torna mais trabalhosa ou mesmo operacionalmente inviável. Neste
caso deve ser realizada eletronicamente, através de um pacote específico para
apuração.
Existem vários, entre eles, o ‘SPSS’, ‘Statistica’, ‘R’ e o “SAS”.
Análise de Dados:
A análise de dados consiste no tratamento estatístico dos dados
registrados, no caso do exemplo, seria estabelecer que os resultados da
apuração fossem informados numa tabela estatística como a descrita abaixo:
É a fase em que se estabelece a forma de representação dos dados e
de acordo com as normas de representação oficial de informações estatísticas
e todas as técnicas para se tirar informações importantes dos registros
apurados (são estabelecidas as tabelas para representar os dados, os gráficos
necessários, porcentagens, totais, médias, técnicas multivariadas, inferências,
etc..).
Na fase da análise de dados, os resultados da pesquisa são trabalhos
para gerar informações úteis, isto é, são os “achados da pesquisa”.
Geralmente, com esta fase concluída pode-se redigir o “Relatório Final
da Pesquisa”.
78

Sexo Contagem
Masculino 6
Feminino 4
Total 10
Emissão de Relatório Final:
Depois da análise de dados, onde os achados da investigação foram
obtidos, redige-se um relatório final de pesquisa, acrescentando aos resultados
da análise de dados: o problema estabelecido no planejamento, a metodologia
da pesquisa, realização de conclusões e tomadas de decisão, referências
bibliográficas e bibliografias.
Comunicação dos Resultados:
Esta etapa do método torna o trabalho do cientista um processo social.
As teorias e conclusões do seu trabalho de pesquisa devem ser relatadas
publicamente e sobreviver a um período de debate, avaliação crítica e a
repetição dos ensaios e testes por outros profissionais competentes. Só assim
os novos conhecimentos são incorporados à ciência universal. Em
conseqüência, tem-se que o conhecimento é um bem público e acervo da
humanidade.
Além do objetivo de socialização dos resultados, os dados precisam ser
comunicados por razões práticas: o homem de negócios precisa dos resultados
da pesquisa para tomar decisões administrativas estratégicas com menos
riscos.
79

Responda às perguntas abaixo:
1. Defina Método.
2. Explique o que é o Método Estatístico?
3. Quais são as fases do Método Estatístico?
4. Quando nasce a necessidade de se realizar um trabalho
estatístico?
5. Qual a primeira fase de um trabalho estatístico?
6. Antes mesmo de ser aplicar o Método Estatístico, o que devem
ser definidos primeiro pelo pesquisador?
7. O que é objetivo de pesquisa?
8. O que é Motivação ou relevância de uma pesquisa?
9. Quais as fases de um planejamento de pesquisa estatística?
10.O que é ‘Projeto de pesquisa’?
11.O que é coletar dados?
12.Quais os tipos de dados?
13.O que são dados primários?
14.O que são dados secundários?
15.O que é crítica de dados?
16.O que é apuração de dados?
17.O que é apuração de manual de dados?
18.Cite dois programas estatísticos que realizam apuração de dados
estatísticos via computador.
19.O que é análise de dados?
20.O que são estabelecidos na análise de dados?
21.Quando são realizadas inferências estatísticas aos resultados
inicialmente encontrados?
22.Qual a importância de se realizar a Comunicação dos Resultados
da Pesquisa?
23.Explique o que seja a tomada de decisão num trabalho
estatístico?
80

24.Escolha um objetivo de pesquisa na sua área de formação,
estabeleça uma finalidade para sua realização e apresente um
“Projeto de Pesquisa”.
81

Unidade V
Séries Estatísticas
Conceito de Séries Estatísticas:
É a representação das informações em forma de tabelas.
Seu objetivo é obter um resumo organizado das informações sobre a
variável: fornecer o máximo de informações em um mínimo de espaço.
Tabela:
É um quadro que resume um conjunto de observações.
A construção de tabelas deve seguir as “Normas de Representação
Tabular do IBGE” (ver anexo II).
As Séries Estatísticas podem ser:
• Séries Temporais;
• Séries Geográficas;
• Séries Especificativas;
• Séries Mistas;
• Distribuições de Frequência.
Séries Temporais:
Uma determinada informação é estudada em função do tempo.
82

Exemplo:
Quantidade de Itens Vendidos de um Produto por uma Loja nos Últimos
10 meses em Mil unidades.
Meses Quantidade de Itens Vendidos
Janeiro
Fevereiro
Março
Abril
Maio
Junho
Julho
Agosto
Setembr
o
Outubro
1
2
2
3
4
4
6
8
8
12
Total 50
Séries Geográficas:
Uma determinada informação é estudada em função de uma região ou
localidade. É feita para apresentar dados de diferentes regiões geográficas.
Exemplo:
Percentual de Pessoas com 10 anos ou Mais que Declaram Rendimento
de Até um Salário Mínimo, Segundo as Grandes Regiões do País.
83

Regiões Percentual
Norte
Nordeste
Sudeste
Sul
Centro-Oeste
32,8
48,0
16,0
18,8
22,3
Brasil 25,3
Fonte: Folha de São Paulo (2002)
Séries Especificativas:
Neste caso a informação em estudo é dividida em categorias que a
especifica.
Exemplo:
Número de Consultas Médicas Segundo Especialidades de Saúde
Realizadas por Funcionários Associados a um Plano de Saúde Conveniado
pela Empresa Empregadora. Junho de 2001.
Especialidades Consultas
Geral
Urologia
Cardiologia
Dermatologia
Ginecologia
Neurologia
Oftalmologia
Ortopedia
Otorrinolaringologia
200
35
151
59
90
83
101
45
29
Total 793
84

Séries Mistas:
São aquelas séries estatísticas resultantes da combinação das séries
estatísticas temporais, geográficas, especificativas ou entre distribuições de
freqüências.
Exemplo:
Taxas de Analfabetismo de Pessoas com 15 anos e Mais, Segundo a
cor, nos Censos Demográficos de 1991 e 2000.
Cor Censos
1991 2000
Branca
Preta
Amarela
Parda
Indígena
Sem
declaração
11,9
31,5
5,4
27,8
5,8
18,7
8,3
21,5
4,9
18,2
26,1
16,1
Brasil 19,4 12,9
Fonte: Retrato do Brasil
85

Distribuições de Frequência:
À cada resultado ou subconjunto de resultados de uma variável
quantitativa são registradas nas células da tabela a freqüência com que foram
observados na coleta de dados.
Tipos de Distribuição de Frequência:
• Distribuição de Frequência Simples;
• Distribuição de Frequência por Classe.
Distribuição de Frequência Simples:
À cada resultado de uma variável quantitativa são registradas nas
células da tabela a freqüência com que foram observadas na coleta de
dados.
Exemplo:
Funcionários de uma Empresa Segundo Idades. Rio de Janeiro,
Julho/2001
Idades
Número de
Funcionários
27 15
32 23
35 32
38 35
42 43
47 28
86

Distribuição de Frequência por Classe:
À cada subconjunto de resultados de uma variável quantitativa são
registradas nas cédulas da tabela a freqüência com que foram observados na
coleta de dados.
É a distribuição de freqüência em que a variável observada está dividida
em classes, que são subintervalos do intervalo total.
Formas de se representar uma Classe:
|—— → inclui à esquerda e exclui à direita
——| → exclui à esquerda e inclui à direita
|——| → inclui ambos
—— → exclui ambos
Exemplo:
Tempo em Segundos dos Gastos por
Funcionários para Preencher Determinado
Formulário
Tempo (em segundos) Número de funcionários
40 |― 45 3
45 |— 50 8
50 |— 55 16
55 |— 60 12
60 |— 65 7
65 |— 70 3
70 |— 75 1
Total 50
Elementos de Uma Distribuição de Frequência:
88

a) Classe: são os subintervalos do intervalo total.
Exemplos:
40 |— 45, primeira classe.
50 |— 55, terceira classe.
70 |— 75, última classe.
b) Limites de Classe: são os valores de classe, sendo:
da esquerda (menor valor) chamado limite inferior.
da direita (maior valor) chamado limite superior.
Exemplo:
55 |— 60
55, limite inferior
60, limite superior
c) Intervalo de Classe (h):
É o comprimento de cada classe.
É obtido pela diferença entre o limite inferior de uma classe e o limite
inferior da classe anterior da classe anterior ou a diferença existente entre o
limite superior de uma classe e limite superior da classe anterior.
O intervalo de classe (h) deve ser uma constante na distribuição de
frequência por classe.
89

Exemplos:
45 → limite inferior da segunda classe.
40 → limite inferior da primeira classe.
Logo, h = 45 – 40 = 5
OU
50 → limite superior da segunda classe.
45 → limite superior da primeira classe.
h = 50 – 45 = 5
d) Ponto Médio (xi):
É a média aritmética simples entre o limite superior e inferior de uma
mesma classe.
Todas as classes têm um ponto médio distinto.
O ponto médio é o representante dos valores contidos em uma classe.
O ponto médio varia de classe para classe.
Exemplo:
Tempo (em segundos) Número de funcionários Pontos Médios (xi)
40 |― 45
45 |— 50
50 |— 55
55 |— 60
60 |— 65
65 |— 70
70 |— 75
3
8
16
12
7
3
1
42,5
47,5
52,5
57,5
62,5
67,5
72,5
Total 50 ────
e) Frequência Simples (fi):
90

Também chamada de frequência absoluta.
É o número de vezes que os valores de uma classe ocorreram na
observação, isto é, a freqüência com que foram observados.
Exemplo:
Tempo (em segundos)
Frequência Simples
(fi)
40 |― 45 3
45 |— 50 8
50 |— 55 16
55 |— 60 12
60 |— 65 7
65 |— 70 3
70 |— 75 1
Total 50
f) Frequência Relativa (fri):
É o quociente entre a frequênica simples da respectiva classe pela
freqüência total.
A soma das freqüência relativas é sempre igual a 1.
91

Exemplo:
Tempo (em segundos) Número de funcionários Frequência Relativas (fri)
40 |― 45
45 |— 50
50 |— 55
55 |— 60
60 |— 65
65 |— 70
70 |— 75
3
8
16
12
7
3
1
0,06
0,16
0,32
0,24
0,14
0,06
0,02
Total 50 1
Observação:
Se quisermos obter a freqüência percentual (fri%), basta multiplicarmos
as frequências relativas por 100.
Exemplo:
Tempo (em segundos) Número de funcionários Frequência Percentual (fri%)
40 |― 45
45 |— 50
50 |— 55
55 |— 60
60 |— 65
65 |— 70
70 |— 75
3
8
16
12
7
3
1
6
16
32
24
14
6
2
Total 50 100
92

g) Frequências Acumuladas (FACi)
É obtida através da adição sucessiva à frequência simples da primeira
classe das frequências simples das classes seguintes. A primeira frequência
simples é a primeira frequência acumulada e a última freqüência acumulada é
o somatório total das freqüências absolutas, isto é, a freqüência total n.
Exemplo:
Tempo (em segundos)
Número de
Funcionários
Frequências Acumuladas
(FAC'S)
40 |― 45
45 |— 50
50 |— 55
55 |— 60
60 |— 65
65 |— 70
70 |— 75
3
8
16
12
7
3
1
3
11
27
39
46
49
50
Total 50 ______
93

1) Classifique as séries estatísticas abaixo:
a)Crianças Não Vacinadas Contra Pólio.1989
Regiões Quantidades
Nordeste
Sudeste
Norte
Centro-Oeste
Sul
512900
299585
148818
124791
105371
Fonte: IBGE
c) Avicultura Brasileira, 1988
Espécie
Número
(cabeças)
Galinhas
Pato, Marrecos
Perus
511834
58888
3823
Fonte: IBGE
94

d) Tempo de Licença Sem Vencimento de Funcionários de uma
Empresa
Tempo (em
dias) Quantidade
1
3
4
5
6
7
8
9
10
10
15
25
31
17
28
5
29
34
e) Comprimentos, em centímetros, de Cobaias de 90 dias
Comprimentos
(cm) Quantidade
19
20,5
23,50
25
25,5
26,0
4
7
1
2
3
5
95

e) Número de Suicídios Ocorridos no Brasil em 1986, Segundo a Causa
Atribuída
Causa Atribuída Nº Suicídios
Alcoolismo
Dificuldade Financeira
Doença Mental
Outro Tipo de Doença
Desilusão Amorosa
Outras
263
198
700
189
416
217
Fonte: IBGE
3) Elabore tabelas estatísticas com os relatórios descritos abaixo:
a) Na Bete Marketing, empresa situada no Rio de Janeiro em 1999, um
estatístico realizou um levantamento do número de consultas de funcionário do
plano de saúde conveniada com a empresa por especialidade médica. Na
ortopedia, foram 200funcionários, na clínica geral foram 432, na urologia foram
154, na psiquiatria foram 133, na ginecologia foram 220 e na dermatologia
foram 90 pacientes.
b) Em 2000, o mesmo profissional do item anterior, resolveu acrescentar
a variável sexo ao seu levantamento e constatou: Na ortopedia foram 130 do
sexo masculino e 100 do feminino; na clínica geral foram 153 do sexo
masculino e 165 do feminino; na urologia foram 145 funcionários; na psiquiatria
foram 112 do sexo masculino e 80 do feminino; na ginecologia foram 129 do
sexo feminino e na dermatologia foram 29 do sexo masculino e 100 do
feminino.
96

c) O levantamento feito pelos nutricionistas de uma fábrica de sabão
revelou a quantidade de refeições fornecidas aos operários nos vários turnos
de trabalho:
Desjejuns: 74052;
Almoço: 72249;
Merenda: 72178;
Jantar: 72523;
Ceias: 72999.
Nas informações, não foram incluídas no total refeições extras,
mamadeiras e dietas especiais. Nas refeições ceias e jantar não são oferecidas
sobremesas.
d) Movimento ambulatorial do hospital das clínicas da UERJ no período
de 1973 a 1975. Em 1973, houve 36.0001 pacientes dos quais 17.885 do sexo
masculino; 5.470 internações e 4.698 altas. Em 1974, 20.001 pacientes foram
do sexo masculino e 18.920 do sexo feminino; as internações foram em
número de 6.667 e as altas 4.667. Em 1975, num total de 39.370 pacientes,
20.263 eram do sexo masculino; as altas foram 5.483 e as internações 7.063.
Quanto aos óbitos foram: 2.264, 1.733 e 1958 nos três anos consecutivos.
e) Os dados abaixo resultaram da coleta de sangue de 100 servidores a
serem admitidos em uma grande empresa em 2000 em Petrópolis.
Tipo O, 15
Tipo A, 45
Tipo B, 35
Tipo AB, 5
f) Os mesmos funcionários foram consultados quanto ao seu fator
sanguíneo e resultou-se:
Rh+
, 55
Rh-
, 40
Observação: cinco, não souberam responder.
4) Os dados abaixo se referem ao peso dos pacientes ao entrar num
97

Spa para dieta de emagrecimento. Estes dados foram levantados por um
auxiliar de administração:
Pesos em Classes (Kg) Pacientes
90 |— 100
100 |— 110
110 |— 120
120 |— 130
130 |— 140
140 |— 150
150 |— 160
160 |— 170
170 |— 180
180 |— 190
190 |— 200
Total
1
5
7
10
13
15
25
32
15
11
4
138
a) Limite inferior da 2a
classe;
b) Limite superior da 4a
classe;
c) Os pontos médios das classes;
d) As frequências relativas;
e) As frequências percentuais;
f) As frequências acumuladas;
g) O número de pacientes cujo peso não atinge a 140 Kg;
h) O número de pacientes cujo peso atinge e ultrapassa a 150 Kg;
i) A percentagem de pacientes com pesos entre 150 e 180 Kg;
j) A percentagem de pacientes com peso maior ou igual a 180 Kg.
98

5) Agrupe os dados abaixo em classes:
Idades de Respondentes a uma Pesquisa de Mercado
6
4 61
6
5 43
4
5
5
4 51
7
4
3
0 100
9
1 75
7
8
6
8 80
6
9
7
2 27
4
0 93
9
9
9
4 78
7
2
5
9 78
9
5 62
4
2
9
6 100
9
5
8
1 84
7
8 103
9
8
6
0 84
9
1
99

Unidade VI
Números Relativos
Dados Absolutos
Os dados estatísticos resultantes da coleta direta da fonte,
sem outra manipulação senão a contagem ou medida são chamados
dados absolutos.
A leitura dos dados absolutos pode ser enfadonha e
inexpressiva; embora esses dados traduzam um resultado exato e
fiel, não têm a virtude de ressaltar de imediato as suas comparações
numéricas. Daí o uso imprescindível que faz a estatística dos dados
relativos.
Dados Relativos
Dados relativos é o resultado de comparação por quociente
(razões) que se estabelecem entre os dados absolutos e têm por
finalidade realçar ou facilitar as comparações entre quantidades.
Traduzem-se os dados relativos, em geral, por meio de,
coeficientes, taxas, percentagens e índices.
100

1-Coeficientes
Os coeficientes são razões entre o número de ocorrências e o
número total (número de ocorrências e número de não-ocorrências).
A
Coeficiente= ——————
A + B
Parte
Coeficiente= ——————
Todo
Exemplos:
Número de nascimentos
Coeficiente de natalidade = ────────────────────────
População total
101

Número de óbitos
Coeficiente de mortalidade = ────────────────────────
População total
No
reservas canceladas
Coeficiente de cancelamento de reservas = ——————————
Reservas totais
2-Taxas
As taxas são os coeficientes multiplicados por uma potência
de 10( 10, 100, 1.000 etc.) para tornar o resultado mais inteligível.
Exemplos:
Taxa de mortalidade = coeficiente de mortalidade X 1000
Taxa de natalidade = coeficiente de natalidade X 1000
Taxa de cancelamento de reservas = Coeficiente de cancelamento
de reservas X 100
102

3-Percentagens
É o número relativo mais empregado: expressa uma relação
da parte com o todo em base 100. Deriva de conceito análogo ao de
coeficiente e taxas, mas se difere porque é sempre calculado
multiplicando-se por 100.
Consideremos a série:
Reservas em Hotéis da Cidade Y
Hotéis Número de Reservas
A 19.286
B 1.681
C 234
Total 21.201
Calculemos as percentagens dos alunos de cada grau:
19.286 X 100
Hotel A → ────────────── = 90,96 = 91,0%
21.201
1.681 X 100
103

Hotel B → ────────────── = 7,92 = 7,9%
21.201
234 X 100
Hotel C → ────────────── = 1,10 = 1,1%
21.201
Com esses dados, podemos formar uma nova coluna na série
em estudo:
Reservas em Hotéis da Cidade Y com Percentagens
Hotéis Número
de Reservas
%
A 19.286 91,0
B 1.681 7,9
C 234 1,1
Total 21.201 100,0
Os valores dessa nova coluna nos dizem que, de cada 100
reservas dos hotéis considerados da cidade, 91 são para o hotel A, 8
aproximadamente para o hotel B e 1 no hotel C.
O emprego da percentagem é de grande valia quando é
nosso intuito destacar a participação da parte no todo.
104

Consideremos, agora, a série:
Reservas em Hotéis da Cidade Y e W
Hotéis Número de
Reservas
Cidade Y
Número de
Reservas
Cidade W
A 19.286 38.660
B 1.681 3.399
C 234 424
Total 21.201 42.483
Qual das cidades tem, comparativamente, maior número de
reservas nos hotéis considerados?
Como o número total de reservas é diferente nas duas
cidades, não é fácil concluir a respeito usando os dados absolutos.
Porém, usando as percentagens, tal tarefa fica bastante facilitada.
Assim, acrescentando na tabela acima as colunas
correspondentes às percentagens, obtemos:
105

Reservas em Hotéis da Cidade Y e W com Percentagens
Hotéis
Cidade Y Cidade W
Reservas % Reservas %
A 19.286 91,0 38.660 91,0
B 1.681 7,9 3.399 8,0
C 234 1,1 424 1,0
Total 21.201 100,0 42.483 100,0
A leitura da acima permite dizer que os hotéis considerados,
comparativamente, contam, praticamente, com o mesmo número de
reservas nas duas cidades em que estão instalados.
Do mesmo modo que tomamos 100 para base de
comparação, também podemos tomar outro número qualquer, entre
os quais destacamos o número 1. É claro que, supondo o total igual
a 1, os dados relativos das parcelas serão todos menores que 1.
Em geral, quando usamos 100 para a base, os dados são
arredondados até a primeira casa decimal; e quando tomamos 1 por
base, são arredondados até a terceira casa decimal.
106

4-Índices
Os índices são razões entre duas grandezas tais que uma não inclui a
outra.
Exemplos:
população
Densidade demográfica = ──────────
Superfície
Índices Econômicos:
Valor total da produção
Produção per capita = ────────────────────
população
consumo do bem ou serviço
Consumo per capita = ────────────────────
população
demanda pelo bem ou serviço
Demanda per capita = ────────────────────
População
renda
Renda per capita = ────────────────────
população
107

receita
Receita per capita = ────────────────────
população
Os dados relativos constituem em técnicas estatísticas que possibilitam
o destaque do que há de mais essencial na informação, o que muitas vezes é
não acontece de imediato com os dados absolutos. A principal vantagem dos
dados na forma relativa é possibilitar comparações de categorias de variáveis
quando o número total em cada categoria é diferente.
108

1)Complete a tabela abaixo:
Empresas No
de
funcionários
Dados Relativos
Por 1 Por 100
A 175 0,098 9,8
B 222
C 202
D 362
E 280
F 540
Total 1.781 1,000 100,0
2)O hotel A registrou 733.986 reservas no início de um “feriadão” e
683.816 no fim do “feriadão”. O hotel B apresentou 436.127 reservas no início
do “feriadão” e 412.457 no fim do “feriadão”. Qual o hotel que apresentou
maior saída de hóspedes?
3)Considerando que Minas Gerais, em 1992, apresentou(dados
fornecidos pelo IBGE):
 População: 15.957.600 habitantes;
 Superfície: 586.624 km2
 Nascimentos: 292.036
 Óbitos: 99.282.
109

Calcule:
a) O índice da densidade demográfica;
b) A taxa de natalidade;
c) A taxa de mortalidade.
4)Em uma escola da zona sul carioca as matrículas totais de alunos no
ano de 2010 foi de 5.000 alunos, dos quais destes contabilizou-se 250
repetentes. Qual o coeficiente de desperdício ou o coeficiente de repetência da
escola para este ano?
5)Foi pesquisado no anuário estatístico do país de 2008 a matrícula
efetiva na 1ª série, em um estado, referente ao ano de 2006, que revelou
50.000 alunos. Como estamos estudando o período curricular de 2006 a 2009,
as quatro primeiras séries do ensino fundamental, foi pesquisado também o
anuário estatístico do país de 2010, onde encontramos a diplomação na 4ª
série referente a 2009 no estado de 10.000 alunos. Qual o coeficiente de
produtividade curricular ou de diplomação ou a taxa de sobrevivência escolar
do estado neste ano?
6)Numa faculdade, o número de salas de aula somavam-se 40.000 e a
escola tem 24.000 alunos. A faculdade funciona em dois turnos. Qual a
densidade aluno/salas de aula por turno desta faculdade?
110

Unidade VII
Gráficos Estatísticos
Conceito de Gráficos Estatísticos :
A Estatística faz uso de recursos numéricos e visuais para representar
os fenômenos. O gráfico é usado para ilustrar ou ressaltar um fenômeno
através de uma imagem, o que o torna de mais fácil compreensão. Sabe-se
que a leitura de um gráfico é mais fácil do que de uma tabela.
É um método de representação de dados estatísticos por meio de
figuras geométricas.
Requisitos Fundamentais de um Gráfico:
o Simples
o Claro
o Exato
Finalidades dos Gráficos:
o Apresentar os dados de modo agradável e claro
o Poupar tempo e esforço na análise
o Dispor os dados de modo a focalizar as comparações num
relance
o Tornar claros os fatos que possam ser objetos de confusão
o Olhando um gráfico você pode ter uma visão mais geral do que
ocorre com sua variável na sua empresa, sem precisar ficar
observando sequências de números intermináveis.
111

Tipos de Gráficos:
o Gráficos de Reclame
o Gráficos de Análise
Gráficos de Reclame:
São os destinados ao grande público. São de fácil interpretação.
Representam todas as séries estatísticas.
Tipos de Gráficos de Reclame:
o Linear;
o Colunas;
o Barras;
o Setograma ou “Pizza”.
Construção dos Gráficos:
Todos os gráficos podem ser facilmente construídos no Excel (inserir →
gráfico → tipo de gráfico) e no programa estatísticos SPSS (menu graphs).
112

1)Gráfico Linear ou de Linha:
É a representação das informações por meio de uma linha. É usado para
representar séries temporais.
Exemplo:
Quantidades de Peças Vendidas de uma
Mercadoria por uma Loja de 2000-07
113

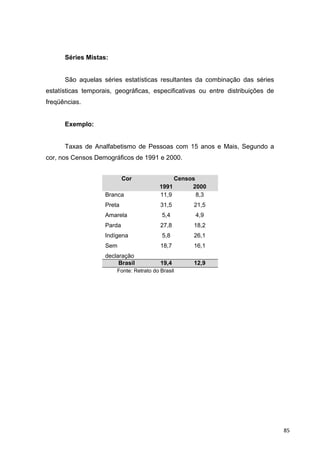
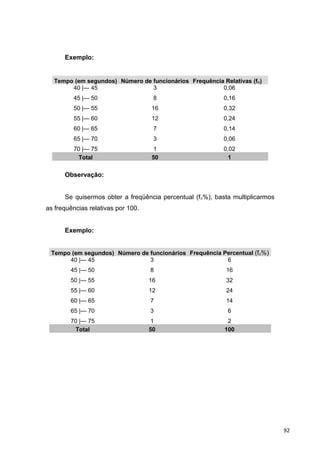
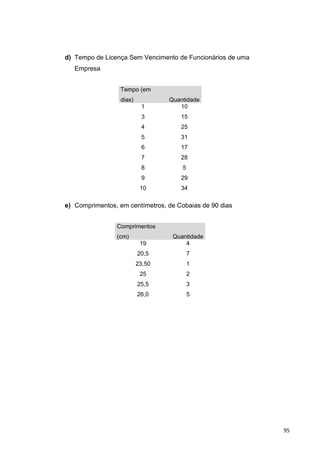
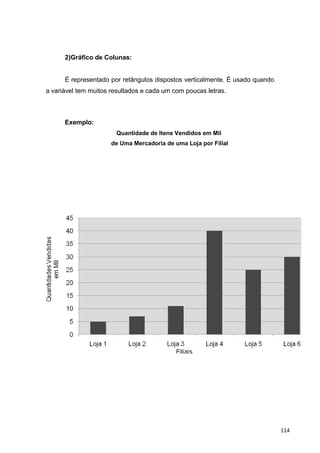
2)Gráfico de Colunas:
É representado por retângulos dispostos verticalmente. É usado quando
a variável tem muitos resultados e cada um com poucas letras.
Exemplo:
Quantidade de Itens Vendidos em Mil
de Uma Mercadoria de uma Loja por Filial
114

3)Gráfico de Barras:
É representado por retângulos dispostos horizontalmente. É usado
quando a variável tem muitos resultados e cada um com muitas letras.
Exemplo:
Acomodação Atual dos Alunos do Bacharelado em Cerâmica
116

4)Gráfico de Setores ou “Pizza”:
A variável é apresentada em um círculo, onde cada resultado da mesma
é uma fatia da ‘pizza’; cada fatia da ‘pizza’ tem tamanho proporcional ao valor
relativo que o seu resultado representa em relação ao total.
A variável deve ter poucos resultados, no máximo cinco categorias.
Exemplo:
Gráficos em Setores Tipo Sanguínea de Funcionários de Uma Empresa
117

Interpretações de Gráficos de Reclame:
A interpretação de gráfico de reclame se dá verificando os máximos e
mínimos, bem como as mudanças bruscas ou as identidades.
Tratando-se de série temporal e respectivo gráfico de linha, observa-se
principalmente a tendência secular do fenômeno, se crescente ou decrescente,
ou ainda, se há oscilação.
Gráfico de Análise:
São gráficos destinados a um público especializado. São gráficos
exclusivos de distribuição de freqüência.
Tipos de Gráficos de Análise:
• Histograma;
• Polígono de Frequência.
Interpretação de Gráfico de Análise:
A forma da distribuição apresentada pelo gráfico é comparada à forma
de distribuições teóricas que fundamentam comportamentos característicos de
variáveis representadas e utilização de inferências estatísticas.
118

1)Histograma:
É a representação gráfica da distribuição de freqüência através de
colunas justapostas de maneira contínua, representando cada coluna uma
classe. Não há, portanto, espaço entre as colunas, ou seja, onde termina uma
classe, imediatamente inicia-se outra.
2) Polígono de Frequência:
É uma linha poligonal que é resultado de interligação de pontos que
representam os valores de cada classe, isto é, os pontos médios de cada
subintervalo do intervalo total. Também como o histograma, representa uma
distribuição de freqüência com intervalo de classe.
Exemplo:
119

Responda às perguntas abaixo:
1. O que é um gráfico?
2. Cite 2 finalidades de se construir um gráfico?
3. Quais são gráficos de reclame?
4. Cite os tipos mais usuais de gráficos de reclame.
5. Qual o gráfico mais indicado para se representar uma série
temporal?
6. Como se interpreta um gráfico de reclame?
7. Quando usamos o gráfico de colunas?
8. Quando usamos o gráfico de barras?
9. Que gráfico relaciona a proporção que cada categoria de uma
variável representa em relação ao total?
10.Quando usamos o gráfico de ‘pizza’?
11.O que é um gráfico de análise?
12.Quais os tipos mais usuais de gráfico de análise?
13.Como se interpreta um gráfico de análise?
14.Faça no Excel um gráfico adequado para cada série estatística da
questão 1 dos exercícios propostos da Unidade Séries
Estatísticas.
120

Unidade VIII
Estudo das Distribuições de Frequência
Conceitos de Medidas de Distribuições de Frequências:
A partir de agora iremos nos deter nos aspectos quantitativos de uma
distribuição de frequência. Estudaremos os parâmetros característicos de uma
distribuição de frequência. Assim como as Séries Estatísticas e os Gráficos
Estatísticos estas medidas têm como objetivo resumir e sintetizar determinadas
informações sobre as distribuições de frequência.
As medidas de uma distribuição de frequências são parâmetros
característicos que informam sobre a tendência geral, a dispersão e a forma de
uma distribuição de frequência.
Medidas de Tendência Central:
Objetivo:
Elas descrevem o nível geral dos dados coletados, isto é, elas informam
a tendência dos dados, dos valores da série.
Por descrever o padrão geral dos dados, elas podem ser usadas para
resumir e representar os dados das quais foram calculadas.
1ª) Média Aritmética(X)
É a razão entre o somatório dos valores observados e o número deles.
Portanto, se tivermos:
X1; X2; X3; .... Xn, a Média será:
121

_
X = ΣX
n
Onde n é o número total de dados observados.
Média – Somar todos os Xi e dividir pela quantidade deles.
Exemplos:
1) 6,5,5,6,8
_
X = (6+5+5+6+8)/5 =6, O nível geral desses números é 6.
2)Os valores relativos a atitudes de 31 estudantes frente a um grupo
minoritário, foram dispostos na seguinte distribuição de freqüência:
Quanto maior o valor, mais favorável à atitude minoritária
Valores Xi Fi Xifi
7 3 21
6 4 24
5 6 30
4 7 28
3 5 15
2 4 8
1 2 2
Σ 31 128
_ Σ Xi. Fi
X = ──────
n
_
Então : X = 128/31 =4,1
122

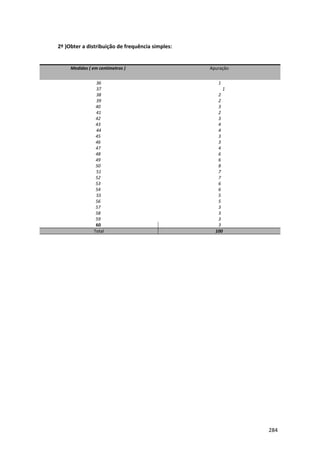
3)Distribuição por Intervalo de Classe
‘Desempenho de Funcionários no Treinamento de uma Tarefa ’
Notas fi xi xifi di difi
20 |—| 29 2 24,5 49.0 -4 -8
30 |—| 39 9 34,5 310.5 -3 -27
40 |—| 49 11 44,5 489.5 -2 -22
50 |—| 59 15 54,5 817.5 -1 -15
60 |—| 69 17 64,5 1096.5 0 0
70 |—| 79 16 74,5 1192.0 1 16
80 |—| 89 7 84,5 591.5 2 14
90 |—| 99 3 94,5 283.5 3 9
Total 80 ─── 4830 ─── -33
Pelo Processo Longo:
X = Σxifi X = 4830/80 = 60,4
n
Pelo Processo Breve:
X = x0 +h [Σdifi] X = 64,5 + 10[-33] = 60,4
n 80
Onde:
─
xo = ponto médio da classe em que o di é igual à zero.
2ª) Mediana (Me):
123

É o valor do rol que ocupa o centro da distribuição, ou seja, é o valor que
divide a distribuição ao meio.
Rol: são os dados em ordem crescente ou decrescente. O mais usado é
em ordem crescente.
Exemplos
1)3,7,4,12,14,10,15
Rol: 3,4,7, , 12, 14, 15
É a mediana Me. É o nível geral destes números.
2) 3,4,7,12,15,10,18,14
Rol: 3,4,7, ,14,15,18
O 10 e o12 são valores que ocupam o centro distribuição. A mediana
será a média entre estes dois valores.
Me= (10+12)/2 = 22/2 =11
10
Me=10
10,12
Me = 11
124

3)Trinta e uma crianças matriculadas numa 3ª série do 1° grau de um
bairro da zona oeste indicaram numa pesquisa o número de irmãos e/ou irmãs
que viviam com cada um deles em casa. Os dados resultantes foram dispostos
na tabela abaixo. Calcule a mediana:
N° de irmãos e/ ou
irmãs
Fi Faci
5
4
3
2
1
6
7
9
5
4
6
13
22 16<22
27
31
Σ 31 -
Processo de cálculo:
1º) Calculam-se as Fac’s:
2º) Calcula-se o elemento mediano (EMe), da seguinte forma:
EMe= n/2, se n for par.
EMe= (n+1)/2, se n for ímpar.
3º)Identifica-se Me, de tal forma:
EMe<FACi
EMe= (n+1)/2 = 31+1 =32/2 = 16
2
Me = 3
125

4)
Calcular a Mediana da Distribuição:
Xi Fi Faci
12
14
15
16
17
20
Σ
1
2
1
2
1
1
8
1
3
4 4=4
6
7
8
-
EMe = 8/2 = 4
Me = (15+16)/2 = 15,5
126

5)
‘Estatura de 40 Candidatos a Cargos de Garis da COMLURB’
Estatura(cm
)
Fi Faci
150 |— 154
154 |— 158
158 |— 162
162 |— 166
166 |— 170
170 |— 174
4
9
11
8
5
3
4
13
5) 20 < 24, Classe da Me
32
37
40
Σ 40 -
Processo de Cálculo:
1º) Calculam-se as Fac’s
2º) Calcula-se o EMe
3º) Identifica-se a classe da mediana tal que:
4º) Aplica-se a fórmula:
Me = li + h [ EMe – ‘FAC ]
fmed
EMe ≤ Faci
127

Onde :
Me = mediana.
Li = limite inferior da classe da mediana.
H = intervalo de classe.
EMe =elemento mediano.
‘Fac = 128reqüente128 acumulada anterior à classe da mediana.
Fmed = freqüência absoluta da classe da mediana.
EMe = 40/2 = 20
Me = li + h [ EMe – ‘FAC ]
fmed
Me =158 + 4[ 20 – 13 ] = 160,5
11
3ª) Moda ( Mo)
É o valor que possui a maior freqüência em um conjunto de dados ou
distribuição.
Exemplos:
1) 7,8,9,10,10,10,11,12,13 e 15
Mo = 10
2) 3,5,8,10,12,13
Não há – distribuição amodal
128

3) 2,3,4,4,4,5,6,7,7,7,8,9
Mo = 4 e Mo = 7 – distribuição bimodal
4) 6,6,6,6,6,6
Não tem valor mais freqüente. Distribuição Amodal.
5)3,3,3,8,6,6,6,10,15,15,15
Mo = 3 Mo = 6 Mo = 15
Distribuição Trimodal
6)Dada a distribuição de frequência abaixo, calcule a moda
Xi Fi
3
5
9
12
Σ
2
7
13
8
30
Mo = 9
7)
129

Xi fi
3
8
6
10
15
Σ
3
1
3
1
3
11
Mo = 3 Mo = 6 Mo = 15, distribuição trimodal
8) Calcule a Moda da Distribuição de Salários de Funcionários de uma
Empresa
Salários (R$) fi
500 |— 700
700 |— 900
900 |— 1100
1100 |— 1300
1300 | — 1500
1500 |— 1700
1700 |— 1900
Σ
18
31 Classe Mo
15
3
1
1
1
70
130

1ª) Moda bruta: É o ponto médio da classe modal.
Então: Mo = (700+900)/ 2 = R$ 800,00
2ª) Moda de king:
Mo = li + h [ fpost ]
────────────
fant + fpost
M0 =700 + 200 [ 15 ] = R$ 790,9
──────
18+15
3ª) Moda de Czuber:
Mo = li + h [ f.máx. – f.ant. ]
──────────────────
2.fmáx – (f.ant + f.post.)
Mo = 700+ 200 [ 31– 18 ]
──────────────────
(2 x 31) – (18 + 15)
Mo = R$ 789,7
131

Onde:
Mo= moda
li = limite inferior da classe modal.
f.máx. = frequência máxima
f.post. = frequência posterior à classe modal.
f.ant. = frequência anterior à classe modal.
Uso das Medidas de Tendência Central:
A medida ideal em cada caso é aquela que melhor representa a maioria
dos dados da distribuição de frequência.
Passos para a Escolha da Melhor Medida:
1. Verifique se a distribuição é de variável qualitativa. Se sim, a melhor
medida é a Moda.
2. SE não for de variável qualitativa, verifique se ela é de alta ou média
dispersão. Se for de alta dispersão, a melhor medida é a mediana ou a moda.
Se não for, isto é, de baixa dispersão, a melhor medida é a média.
132

Medidas de Posição (Separatrizes):
São valores que ocupam determinados lugares em um ROL:
Objetivo:
É útil classificar um determinado elemento no grupo a que pertence.
1ª) Os Quartis (Qi):
São valores que dividem uma distribuição em 4 partes iguais.
Há, portanto, 3 quartis.
a) Q1 – (1º quartil) – é o valor situado de tal modo na série que 25% dos
dados são menores ou iguais a ele, 75% são maiores que ele.
b) Q2 – (2º quartil) – é o valor situado de tal modo na série que 50 % dos
dados são menores ou iguais a ele e 50% são maiores.
c) Q3 – (3º quartil) – são valores situados de tal forma na série que 75%
dos dados são menores ou iguais a ele e 25% são maiores.
A faixa de salários que vai de Q1 a Q3, e que concentra a maioria dos
valores da distribuição é chamada faixa salarial.
133

Cálculo dos Quartis:
1º) Dados Não Agrupados em Classe:
Quando os dados não estão agrupados em classe, para determinar as
separatrizes usamos uma regra de três que irá nos indicar a posição do
elemento no conjunto de dados. Da seguinte forma:
100% dos dados ------------------- n
Porcentagem da separatriz -------------------EQi
em que:
n=número de elementos do conjunto de dados
EQi= posição do elemento no ROL
Exemplo:
Para o seguinte conjunto de dados encontre os primeiro e terceiro
quartis.
i 1 2 3 4 5 6 7 8 9 10 11 12 13 14
x 3 5 10 13 14 19 20 28 28 29 37 45 54 67
134

Cálculo do 1º Quartil:
100% ------------- 14
25% ------------- EQ1
EQ1 = (25 . 14)/100 ⇒ EQ1= 3,5. Como não existe a posição 3,5 então
aproxima-se para o valor inteiro superior, resultando em EQ1 = 4. Sendo
assim, o valor do Q1 neste conjunto de dados será Q1=13.
Cálculo do 3º Quartil:
100% ------------- 14
75% ------------- EQ3
EQ3= (75 . 14)/100 ⇒ EQ3 = 10,5. Como não existe a posição 10,5 então
aproxima-se para o valor inteiro superior, resultando em EQ3 = 11. Sendo
assim, o valor do Q1 neste conjunto de dados será Q3=37.
A posição da separatriz é um número inteiro, ou seja, sem casas
decimais, dentro do conjunto de dados. Assim, sempre que o valor calculado
para a separatriz resultar em casas decimais, este valor será aproximado para
o inteiro superior.
135

2º) Dados Agrupados em Classe:
Atenção:
Quando os dados estão agrupados em classe, para determinar os
quartis, usamos a mesma fórmula da mediana, adaptada, onde o elemento
mediano, EMe, é substituído por EQi, elemento quartílico, dado pela fórmula:
EQi = i . n , onde i é o número de ordem dos quartis 1,2 ou 3.
4
Exemplo:
- Determinar a faixa salarial dos empregados dessa empresa.
Salários
(R$)
Fi FACi
500 |— 700
700 |— 900
900 |— 1100
1100 |— 1300
1300 | — 1500
1500 |— 1700
1700 |— 1900
Σ
15
43
18
5
1
1
1
84
15
58
76
81
82
83
84
_
A faixa salarial dos empregados da empregados da empresa é o
intervalo que vai de Q1 a Q2, então:
136

EQ1 = 1 x 84 = 21
4
Q1= li + h [ EQ1 – ‘Fac ]
────────────
FQ1
Q1= 700 + 200 [ 21 – 15 ]
──────── = R$ 728,00
43
EQ3 = 3 x 84 = 63
4
Q3= li + h [ EQ3 – ‘Fac ]
FQ3
Q3= 900 + 200 [ 63 – 58 ] = R$ 956,00
────────
18
Faixa Salarial: R$ 728 a R$ 956
2ª) Os Percentis (Pi):
Denominamos percentis os 99 valores que separam a série em 100
partes iguais.
Indicamos:
P1,P2,........P32..........,P99
É evidente:
137

P50 = Me = Q2; P25 = Q1 ; P75 = Q3
Faixa que concentra a maior parte dos valores:
P25 a P75
Se 20% dos funcionários com menores salários recebem cesta básica
pela empresa, qual o maior salário para recebimento desse benefício?
Solução:
EP20 = in = 20 x 84 = 16,8
100 100
Pi= li + h [ EPi – ‘Fac ]
FPi
P20 = 700 + 200 [ 16,8 – 15 ] = R$ 708,00
43
Medidas de Dispersão:
Objetivo:
Caracterizar se os valores da distribuição são homogêneos ou
heterogêneos.
1ª) Amplitude Total (R):
Chamando:
Xmax = maior valor da distribuição
138

Xmin = menor valor da distribuição
A amplitude total é a diferença entre e o menor valor observado.
Então:
R = Xmax - Xmin
Quanto maior a amplitude total mais heterogêneo são os dados entre si.
Exemplos:
1) 15, 12, 10, 17, 16
R = 17 – 10 = 7
2) Considere a série abaixo que representa a temperatura registrada
durante 30 dias numa região.
Temperatura (ºC) fi
10
15
20
30
40
Σ
2
6
12
7
3
30
R = 40 – 10 = 30º c
139

3) Considere a distribuição abaixo:
Estaturas (cm) fi
150 |— 154
154 |— 158
158 |— 162
162 |— 166
166 |— 170
170 |— 174
Σ
4
9
11
8
5
3
40
R = 174 – 150 = 24 cm
Uso e Desvantagens da Amplitude Total:
A amplitude total o inconveniente de só levar em conta os 2 valores
extremos da série, descuidando-se do conjunto de valores intermediários, o
que quase sempre invalida a precisão e eficácia do resultado. Ela é apenas
uma indicação aproximada da dispersão ou variabilidade.
Faz- se uso da amplitude total quando se quer determinar amplitude ou
variação da temperatura em um dia ou ano , em controle da qualidade ou
quando a compreensão popular é mais importante que a exatidão e eficácia.
140

2ª) Variância (S2
):
É a média aritmética dos quadrados dos desvios em relação média da
distribuição.
Desvio (di) – é a diferença de cada valor da distribuição de sua média:
──
di = (Xi – X ), com i=1,n
O seu quadrado vem:
──
d2
i = (Xi – X )2
Temos que a sua média aritmética é a variância:
n ──
Σ(Xi ─ X )2
i=1
S2
= ──────────────
n
Exemplos:
1) Notas de uma turma:
5; 7; 8; 6,5
X = (5+7+8+6,5) = 6,6 média
4
(5 - 6,6)2
= (-1,6)2
= 2,56
(7 - 6,6)2
= (0,4)2
= 0,16
(8 - 6,6)2
= (1,4)2
= 1,96
(6,5 - 6,6)2
= (0,1)2
= 0,01
141

n ──
Σ(Xi ─ X )2
i=1
S2
= ──────────────
n
4,69
S2
= ────────────── = 1,17
4
2)Tempo de Sobrevivência de Determinado Aparelho Cirúrgico em Anos.
Xi (anos) fi Xifi Xi
2
fi
2
3
5
6
7
1
4
5
3
2
2
12
25
18
14
4
36
125
108
98
Σ 15 71 371
Neste caso, a variância é dada por:
ΣX2
. fi – Σ(Xi . fi)2
──────
n
S2
= ────────────────────
n
Então:
142

371 - (71)2
──────
15
S2
=────────────────── = 2,33
15
3)Um psicólogo foi encarregado de treinar operários para o trabalho em
uma fábrica. Após o treinamento ele deu uma nota a cada operário pelo seu
aproveitamento e os resultados foram:
Notas Fi xi xiFi xi
2
Fi di diFi di
2
Fi
0 |— 2
2 |— 4
4 |— 6
6 |— 8
8 |— 10
5
8
14
10
7
1
3
5
7
9
5
24
70
70
63
5
72
350
490
567
-2
-1
0
1
2
-10
-8
0
10
14
20
8
0
10
28
Σ 44 - 232 1484 - 6 66
Processo Longo:
Σx2
. fi – Σ(xi . fi)2
──────
n
S2
= ───────────────────────
n
1484 - (232)2
──────
44
S2
= ────────────────── = 5,93
44
143

Processo Breve:
S2
= [Σ d2
i fi - (Σdi fi)2
] x (h2
/n)
n
Então:
S2
= [66 - (6)2
] x (22
/44) = 5,93
44
3ª) Desvio Padrão(S):
É raiz quadrada da variância, definida para que a medida de
variabilidade fique na mesma escala da variável original.
Então dos exemplos anteriores temos:
S = √1,17 = 1,08
S = √2,33 = 1,53
S = √5,93 = 2,44
144

4ª) Coeficiente de Variação(CV):
Operacionalmente, é a razão percentual entre o desvio padrão e a
média. Seu resultado não é da mesma qualidade da escala, ao contrário, é o
resultado que expressa em percentagem , a fração que o desvio padrão é
média.
É definido como:
CV = S . 100%
──────
x
Tem-se que:
CV ≤ 15%, baixa dispersão (dados homogêneos).
15% < CV ≤ 30%, média dispersão.
CV > 30%, alta dispersão (dados heterogêneos).
Ex.: O peso de 20 pessoas revela que os dados têm baixa dispersão.
X = 51kg
S = 6,14 Kg
Logo, CV = 6,14 . 100% = 12,04%, baixa dispersão.
─────
51
145

Uso do coeficiente de variação na Comparação de Grupos
Usa-se o coeficiente de variação para comparar a dispersão:
o De populações com estudos envolvendo variáveis diferentes, isto
é, com universos em escalas de medidas distintas (pessoas,
alturas);
o De população distintas (crianças, adultos);
o De populações com desvios-padrão iguais, mas com médias
diferentes.
Exemplos:
1)Numa Clínica, o salário médio dos homens é de R$ 400,00 com desvio
padrão R$150,00 e o das mulheres é de R$300,00 com desvio padrão
R$120,00. Qual o grupo mais heterogêneo quanto ao salário?
CVH = 150 . 100% = 38%, alta dispersão.
400
CVM = 120 . 100% = 40%, alta dispersão.
300
Os salários das mulheres variaram mais. O grupo mais heterogêneo é o
das mulheres.
146

2)Tomemos os resultados das medidas das estaturas e dos pesos de
uma mesma a população de indivíduos.
Variáveis X S
Estaturas 175 cm 5,0 cm
Pesos 68 kg 2,0 kg
Qual o grupo menos disperso?
CVE = 5,0 . 100% = 2,5%, baixa dispersão.
175
CVp = 2,0 . 100% = 2,94%, baixa dispersão.
68
A distribuição menos dispersa foi das estaturas.
3 – Sejam duas séries, em que se tenha, respectivamente:
x1 = 700 mm e S1 = 20 mm
x2 = 100 mm e S2 = 20 mm
CV1 = 20 . 100% = 2,85%, baixa dispersão.
700
CV2= 20 . 100% = 20%, média dispersão.
100
Coeficiente de variação é utilizado nesse caso para a comparação dos
grupos, porque tem médias diferentes e o mesmo desvio padrão.
147

Uso do Coeficiente de Variação na Escolha entre a Média e a
Mediana para Representar os Dados de uma Distribuição de
Freqüência:
Para efeitos práticos, costuma-se considerar que CV superior a 30%
indica alto grau de dispersão, consequentemente pequena representatividade
da média. Enquanto para valores inferiores a 30%, a média será tanto mais
representativa do fato quanto menor for o valor de seu CV.
Então:
CV > 30, a mediana ou a moda.
CV ≤ 30, a média.
Observação:
Para qualificar a dispersão de uma distribuição é mais proveitoso CV,
mas não devemos deduzir que a variância e o desvio padrão careçam de
utilidade. Pelo contrário, são medidas muito úteis no tratamento de assuntos
relativos à inferência estatística.
148

Medidas da Forma de uma Distribuição de Freqüência:
Indica a forma de curvas de freqüências com vistas à comparação da
forma da distribuição de freqüência obtida em uma pesquisa empírica com as
de distribuições de frequências teóricas.
Exemplo:
É muito usual em pesquisa estatística a comparação da forma de curvas
de frequências empíricas com a forma da “Curva Normal”, de importância vital
na fundamentação no Cálculo das Probabilidades e na Teoria da Inferência
Estatística.
As duas medidas que se prestam ao objetivo acima são: assimetria e
curtose.
Curva Normal
Muitos dos fenômenos da natureza, quando medidos de uma amostra
boa, geralmente apresentam sua distribuição de freqüência com perfil
semelhante a uma curva em sino, denominada Curva Normal.
A curva normal tem forma de sino, é unimodal e é simétrica em relação à
média, ou seja, se passarmos uma linha exatamente pelo centro da curva
teremos duas metades perfeitamente iguais.
Assim:
149

A importância da curva normal se dá em virtude dela se adequar bem a
diversas situações práticas, isto é, são vários os fenômenos que seguem uma
distribuição normal ou se aproximam de sua forma. Além desse fato, a grande
importância da curva normal é que ela é pressuposto básico para modelagem
de estimativas alvos de significância estatística.
Assimetria ou Distorção (As):
É o estudo do grau de enviezamento ou distorção da curva de
frequência. O valor enviesado caracteriza o grau de assimetria de uma
distribuição em torno de sua média.
Tipo de Assimetria:
o Assimetria Positiva;
o Assimetria Negativa;
o Curva Simétrica.
150

a)Assimetria Positiva:Mudaram as figuras
Enviezamento à direita, isto é, cauda mais longa a direita. Um valor
enviesado positivo indica uma distribuição ponta assimétrica que se estende
em direção a valores mais positivos.
Numa distribuição assimétrica positiva, a relação sempre vale:
Mo < Me < X
152

b)Assimetria Negativa:
Enviezamento à esquerda, isto é, cauda mais longa à esquerda. Um
valor enviesado negativo indica uma distribuição com uma ponta assimétrica
que se estende em direção a valores mais negativos.
Numa distribuição assimétrica negativa, a relação sempre vale:
X < Me < Mo
153

c)Simétrica:
Não há enviezamento. É uma característica da “Curva Normal”.
Numa distribuição simétrica a relação sempre vale:
X = Me = Mo
Coeficiente de Assimetria de Pearson:
Existem outros, mas estudaremos os de Pearson. Existem 2 coeficientes
de Pearson.
───
X ─ Mo
1º ) As= ─────────────
S
───
3( X - Me )
2º ) As= ─────────────
S
Em função dos resultados acima dos coeficientes, é possível determinar
154

o comportamento da curva de frequência em dois aspectos:
1º) Se:
As = 0, a distribuição é simétrica.
As > 0, a distribuição é assimétrica positiva.
As < 0, a distribuição é assimétrica negativa.
2º) Se:
/ As / ≤ 0,15, distribuição praticamente simétrica.
0,15 < / As / ≤ 1, assimetria moderada.
/ As / > 1, forte assimetria.
Exemplos:
As= 0,12, curva aproximadamente simétrica
As= -0,12, curva aproximadamente simétrica
As= 0,25, curva assimétrica positiva moderada
As= -0,25, curva assimétrica negativa moderada
As= 1,2, cursa de forte assimetria positiva
As= -1,2, cursa de forte assimetria negativa
155

Exemplo:
1)Determinar o coeficiente de assimetria da distribuição abaixo e concluir
sobre o seu grau de enviezamento:
Classes fi
50 |— 60
60 |— 70
70 |— 80
80 |— 90
90 |— 100
15
20
30
20
15
Σ 100
Calculando, temos:
X = 75
Mo = 75
S = 12,65
_
As = ( X – Mo ) / S = ( 75 – 75 ) / 12,65 = 0
A distribuição é simétrica
156

2)Dizer se a distribuição abaixo pode ser ajustada pela curva normal,
analisando o seu grau de assimetria:
Classes fi
3 |— 8
8 |— 13
13 |— 18
18 |— 23
5
15
20
10
Σ 50
Temos:
X = 14
Mo = 15
S = 4,5
──
As = x – Mo = 14– 15 = - 0,22, As = - 0,22
S 4,5
/- 0,22 / - assimetria negativa moderada. A distribuição não pode ser
ajustada à curva normal.
157

Coeficiente Momento de Assimetria(MAS):
n
MAS = ──────────── . M3
(n-1)(n-2)
Tem-se que:
n ──
M3 = [Σ( Xi – X)3
/ S3
]
i=1
1º) Se:
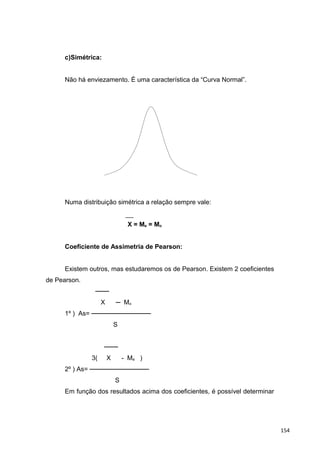
MAs = 0, a distribuição é simétrica.
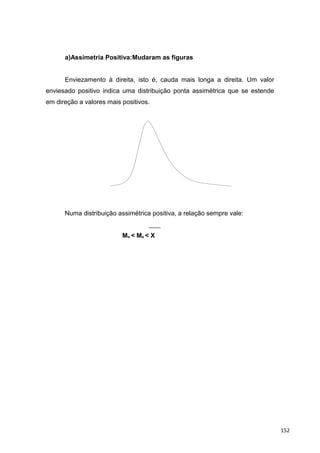
MAs > 0, a distribuição é assimétrica positiva.
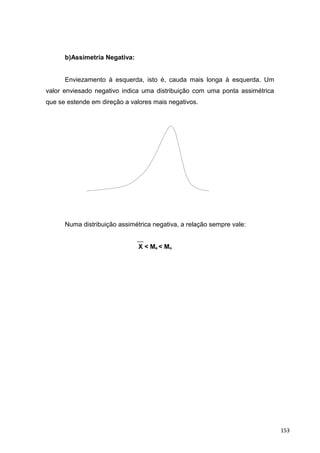
MAs < 0, a distribuição é assimétrica negativa.
2º) Se:
/ MAs / ≤ 0,15, distribuição praticamente simétrica.
0,15 < / MAs / ≤ 1, assimetria moderada.
/ MAs / > 1, forte assimetria.
158

Exemplo 1:
Sejam as duas séries abaixo que representam o nível de satisfação de
clientes usuários da Net com os planos NET TV e NET VIRTUAl. Qual o grau
de assimetria das variáveis?
Grau de Satisfação de Clientes com os Planos NET TV e NET
VIRTUAL da NET
NET TV(X) NET VIRTUAl(Y)
1 1
2 1
2 2
2 2
2 2
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
4 4
4 4
4 4
4 5
5 5
159

Solução:
1º ) Verificando o grau de assimetria da variável X:
X (X-media)3
[(X-media) 3
/S3
1 -8 -10.35
2 -1 -1.29
2 -1 -1.29
2 -1 -1.29
2 -1 -1.29
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
4 1 1.29
4 1 1.29
4 1 1.29
4 1 1.29
5 8 10.35
Soma 0.00 0.00
Média 3
S 0.92
20
MAS = ──────────── . 0 = 0, distribuição simétrica
(20-1)(20-2)
160

2º )Verificando o grau de assimetria da variável Y:
Y (Y-média)3
[(Y-média) 3
/S3
1 -8 -6.42
1 -8 -6.42
2 -1 -0.80
2 -1 -0.80
2 -1 -0.80
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
4 1 0.80
4 1 0.80
4 1 0.80
5 8 6.42
5 8 6.42
Soma 60.00 0.00
Média 3
S 1.08
20
MAS = ──────────── . 0 = 0, distribuição simétrica
(20-1)(20-2)
161

Exemplo 2: Vamos calcular o MAS:
Declarações de Despesas feitas pelos Executivos de uma
Empresa
(Em 100 Reais)
Classes
Fi xi
──
[(x – xi) / s ]3
──
[(x – xi) / s ]3
fi
00 |— 15 12 7,5 - 3,58 - 42,96
15 |— 30 23 22,5 - 0,59 - 13,57
30 |— 45 26 37,5 0,00 0,00
45 |— 60 18 52,5 0,16 2,88
60 |— 75 13 67,5 1,90 24,70
75 |— 90 8 82,5 7,20 57,65
Total 100 ── ── 28,65
Solução:
Neste caso, quando a distribuição vem em intervalo de classe
deveremos fazer umas modificações em M3:
n ──
M3 = [Σ( xi – X)3
/ S3
] fi
i=1
Onde:
xi = ponto médio da classe i;
fi = freqüência simples da classe i.
162

Temos:
_
X = 40,65
S = 21,67
n
MAS = ──────────── . M3
(n-1)(n-2)
MAs = 100 . 28,65 = 0,30
( 100 - 1)(100-2)
Assimetria positiva moderada.
163

2º) Curtose (K):
É o estudo do grau de achatamento da curva de frequência. A curva de
frequência é comparada à curva normal padrão. A curtose caracteriza uma
distribuição em cume ou plana se comparada à distribuição normal padrão.
De acordo com o grau de curtose utilizamos três classificações para as
curvas de freqüência:
Mudou a figura
Leptocúrtica
Mesocúrtica
Platicúrtica
164

Então:
 Mesocúrtica: é aquela que denominamos de padrão, não é nem
muito achatada nem muito alongada. A curva normal padrão
tem a característica de ser mesocúrtica, ou seja, segue este
padrão.
 Leptocúrtica: é a curva mais alongada, tem o pico bastante
acentuado quando comparada à curva normal padrão.
 Platicúrtica: é a curva mais achatada, o seu pico é bastante
suave, quase imperceptível, quando comparada à curva
normal padrão.
Assim:
A curva normal padrão tem a característica de ser mesocúrtica.
Coeficiente de Curtose(K):
Para medir o grau de curtose, podemos utilizar o coeficiente:
Q3 - Q1
K = ───────────
2(P90 ── P10)
165

Se:
K = 0,263, distribuição mesocúrtica.
K < 0,263, distribuição leptocúrtica (distribuição em cume).
K > 0,263, distribuição platicúrtica (distribuição plana).
Do exemplo 2, temos:
Q1 = 10,50
Q3 = 17,38
P10 = 8,00
P90 = 20,50
Então:
17,38 ── 10,50
K = ──────────── = 0,270 > 0,263
2(20,50 ── 8,00)
Distribuição platicúrtica ou plana
166

Coeficiente Momento de Curtose (Mk):
Neste coeficiente, a curtose positiva indica uma distribuição
relativamente em cume. A curtose negativa indica uma distribuição
relativamente plana. A curtose será definida da seguinte forma:
n(n+1) 3(n-1)2
MK= [ ─────────── . M4 ] ─ [ ──────── ]
(n-1)(n-2)(n-3) (n-2)(n-3)
Tem-se que:
n ──
M4 = [Σ( Xi – X)4
/ S4
]
i=1
Neste caso, se:
MK=0 , distribuição mesocúrtica
MK>0, distribuição leptocúrtica
MK< 0, distribuição platicúrtica
Observação:
Tanto o MAS quanto o MK podem ser obtidos diretamente na planilha
eletrônica Excel na função inserir função e nas opções “Distorção” e na
função “Curt” para assimetria e curtose respectivamente. A estatística de
Bera-Jarque não está disponível diretamente no Excel.
167

Exemplo 1:
Sejam as duas séries abaixo que representam o nível de satisfação de
clientes usuários da Net com os planos NET TV e NET VIRTUAl. Qual o grau
de curtose entre as variáveis?
Grau de Satisfação de Clientes com os Planos NET TV e NET
VIRTUAL da NET
NET TV(X) NET VIRTUAl(Y)
1 1
2 1
2 2
2 2
2 2
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
3 3
4 4
4 4
4 4
4 5
5 5
168

Solução:
1º ) Verificando o grau de curtose da variável X:
X (X-média) 4
[(X-média)4
/S4
[(X-média)4
/S4
1 16 22.56 22.56
2 1 1.41 1.41
2 1 1.41 1.41
2 1 1.41 1.41
2 1 1.41 1.41
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
3 0 0.00 0.00
4 1 1.41 1.41
4 1 1.41 1.41
4 1 1.41 1.41
4 1 1.41 1.41
5 16 22.56 22.56
Soma 40.00 56.41 56.40
Média 3
S 0.92
169

n(n+1) 3(n-1)2
MK= [ ─────────── . M4 ] ─ [ ──────── ]
(n-1)(n-2)(n-3) (n-2)(n-3)
20(20+1) 3(20-1)2
MK= [ ─────────── . 56,40] ─ [ ──────── ]
(20-1)(20-2)(20-3) (20-2)(20-3)
20.21 3(19)2
MK= [ ─────────── . 56,40 ] ─ [ ──────── ]
(19)(18)(17) (18)(17)
420 3.361
MK= [ ─────────── . 56,40 ] ─ [ ──────── ]
5814 (18)(17)
420 1083
MK= [ ─────────── . 56,40 ] ─ [ ──────── ]
5814 306
MK= 4,08 – 3,54 = 0,54, distribuição leptocurtica ou cume
170

2º ) Verificando o grau de curtose da variável Y:
Y (Y-média) 4
[(Y-média)4
/S4
1 16 11.93
1 16 11.93
2 1 0.75
2 1 0.75
2 1 0.75
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
3 0 0.00
4 1 0.75
4 1 0.75
4 1 0.75
5 16 11.93
5 16 11.93
Soma 70.00 52.22
Média 3
S 1.08
171

n(n+1) 3(n-1)2
MK= [ ─────────── . M4 ] ─ [ ──────── ]
(n-1)(n-2)(n-3) (n-2)(n-3)
20(20+1) 3(20-1)2
MK= [ ─────────── . 52,22 ] ─ [ ──────── ]
(20-1)(20-2)(20-3) (20-2)(20-3)
20.21 3(19)2
MK= [ ─────────── . 52,22] ─ [ ──────── ]
(19)(18)(17) (18)(17)
420 3.361
MK= [ ─────────── . 52,22] ─ [ ──────── ]
5814 (18)(17)
420 1083
MK= [ ─────────── . 52,22] ─ [ ──────── ]
5814 306
MK= 3,77 – 3,54 = 0,23, distribuição leptocúrtica
172

Exemplo 2: Vamos calcular o Mk:
Declarações de Despesas feitas pelos Executivos de Uma Empresa
(Em 100 Reais)
Classes
Fi xi
──
[(x – Xi) / s ]4
──
[(x – Xi) / s ]4
Fi
00 |— 15 12 7,5 5,48 65,76
15 |— 30 23 22,5 0,49 11,27
30 |— 45 26 37,5 0,00 0,00
45 |— 60 18 52,5 0,09 1,62
60 |— 75 13 67,5 2,36 30,68
75 |— 90 8 82,5 13,91 111,28
Total 100 - - 220,61
Solução:
Ajustes análogos ao do momento de assimetria devem ser feitos no
momento de curtose:
Temos:
_
X = 40,65 e S = 21,67
n(n+1) 3(n-1)2
MK= [ ─────────── . M4 ] ─ [ ──────── ]
(n-1)(n-2)(n-3) (n-2)(n-3)
100(100+1) 3(100-1)2
MK= [ ─────────── . 220,61 ] ─ [ ──────── ] = -0,72
(100-1)(100-2)(100-3) (100-2)(100-3)
Distribuição platicúrtica ou plana.
173

Diferenças da Curva Normal Original e Curva Normal Padrão
Os pesquisadores quando falam de curva normal, tipicamente entendem
a curva normal padronizada, a qual é definida pela simetria e pela curtose. Mas
a curva normal original é definida exclusivamente pela simetria, isto é, que as
áreas sob a curva são idênticas em ambos os lados da média: a curva normal
original é unimodal(tem apenas um pico) e simétrica. Assim, todas as curvas da
figura abaixo são normais, porque têm um pico somente e são simétricas,
embora os desvios sejam diferentes, provocando diferentes níveis de curtose.
Distribuições Normais:
Média
174

Mais ainda, curvas normais originais podem ter médias diferentes,
desvios-padrão diferentes ou ambas as coisas. A figura abaixo demonstra o
fato respectivamente:
Distribuições Normais com Diferentes Médias e Desvios-padrão:
As distribuições normais originais têm médias e desvios-padrão
diferentes porque trabalham diretamente com os escores originais Xi e os seus
parâmetros fundamentais(média e desvio-padrão). Quem comanda as ações
são os dados empíricos Xi e os seus parâmetros característicos
fundamentais( média e desvio-padrão). Tanto os dados empíricos Xi quanto os
parâmetros característicos variam de pesquisa para pesquisa e, assim, as
curvas normais resultantes serão diferentes.
Para contornar o problema de operacionalizar a curva normal original
com suas diferentes formas, os estatísticos estabeleceram que a partir de
qualquer distribuição normal pudesse transformá-la em uma curva normal de
forma constante, sempre com média 0 e desvio-padrão 1: a curva normal
padrão. Todos os estudos e cálculos que se fizesse em cima da normal
padronizada servirá para a curva normal que o originou.
A vantagem dessa curva padronizada consiste em que alguns
parâmetros já estão automaticamente definidos para qualquer escala de
medida que você utilizar, quais seja, média sempre 0 e variância 1. Além disso,
175

existem tabelas construídas para essa curva que mostram probabilidades
sobre esta curva que vale para a curva normal original de mesma área.
A curva normal padronizada é definida pela assimetria e curtose. A curva
normal padronizada tem a característica de ser mesocúrtica.
Em pesquisas, quando se fala de curva normal, sem maiores detalhes,
normalmente se está falando ou assumindo a curva normal padronizada, isto é,
a curva normal mesocúrtica.
176

Teste de Normalidade:
Na análise de dados, frequentemente iremos nos deparar com a
necessidade de realizar o teste de normalidade de variáveis quantitativas.
Existem vários testes de normalidade, mas um dos mais simples é o teste
chamado de Bera-Jarque. A fundamentação estatística utilizada como base
do teste de Bera-Jarque é dada pela equação:
(MAS)2
(Mk)2
BJ = n [ ──────── + ───────── ] < 6,0 para normalidade
6 24
Onde:
n= tamanho da amostra
Exemplo:
Do Exemplo 1, para o cálculo dos momentos de assimetria e
curtose, temos:
a)Cálculo de Bera-Jarques para Variável X:
(0)2
(0,54)2
BJ = 20 [ ──────── + ───────── ]
6 24
177

(0,54)2
BJ = 20 [ ───────── ] = 20 . 0,01 = 0,20 < 6,0, distribuição normal
24
Cálculo de Bera-Jarques para a Variável Y:
(0)2
(0,23)2
BJ = 20 [ ──────── + ───────── ]
6 24
(0,23)2
BJ = 20 [ ───────── ] = 20 . 0,00 = 0,00 < 6,0, distribuição normal
24
Conclusão:
Tanto a variável X quanto a variável Y tem distribuição normal.
178

Descrição de Dados Estatísticos:
A descrição de dados estatísticos, através de uma distribuição de
freqüência e seus gráficos- polígonos de freqüência e histogramas -
geralmente, não é suficiente. A estatística possui medidas descritivas mais
satisfatórias que resumem, de forma bem sucinta, as informações necessárias
ao estudo da distribuição de freqüência.
Para uma descrição bem informativa são necessárias quatro
medidas diferentes:
1)Uma medida de tendência central que informará o nível geral médio do
grupo.
2)Uma medida de variabilidade que dará notícia da dispersão ou
afastamento dos dados em torno do valor central.
3)Uma medida de assimetria que refletirá a inclinação ou enviezamento
da distribuição dos valores, para a direita ou para a esquerda.
4)Uma medida de curtose que dirá do achatamento da curva obtida com a
distribuição de freqüência.
Essas quatro medidas, que se resumirão em apenas quatro números,
descreverão uma distribuição de freqüência, dispensando gráficos e, até,
mesmo, a própria tabela de distribuição de freqüência, quando se tratar de um
relatório final.
179

1) Calcule a média aritmética dos números:
a) 120,150
b) 17,19,5,10,22
c) 2,8,15,7
d) 7,7,7,7,7,7,7
2) Calcule a mediana dos números:
a) 31,52,22,27,54,55,47,38
b) 31,52,22,27,54,55,47,23
c) 13,14,17,19,10
d) 7,2,5,10,12,18
e)13,23,18
f) 12,24
3)Calcule a moda dos números:
a) 7,5,6,10,7,8,7,37,7,15,7,7,20,13
b)11,15,13,1,9,13,21,13,6,13,13,16
c) 10,10,10,10,10,10,10
d) 26,26,26,17,17,17
e) 28,13,13,15,16,16,16,16,13,8
f) 7,7,7,9,9,9,15,15,15,15,15,1,1,1
g) 8,1,0,0,0,0,2,1,9
h) 5,5,5,5,8,7,7,7,7,9,10,10,10,10
180

4)Trinta embalagens plásticas de mel foram pesadas com precisão de
decigramas. Os pesos, após conveniente agrupamento, forneceram a
seguinte distribuição em gramas:
Xi Frequências
31,5
32,5
33,5
34,5
35,5
36,5
1
5
11
8
3
2
Calcule a média, a mediana e a moda para a distribuição.
5)Dados os dez valores seguintes, calcule a sua média, mediana, moda,
variância, desvio padrão e coeficiente de variação:
7
7
8
5
8
0
7
2
7
0
7
7
7
8
8
2
7
5
8
2
181

6)Ensaios de uma amostra ao acaso de quarenta corpos de prova de
concreto fornecem as seguintes resistências à ruptura:
6
1
65 4
3
4
5
5
4
5
1
74 6
4
3
0
100 9
1
7
5
7
8
6
8
80 6
9
7
2
27 4
0
9
3
9
9
9
4
78 7
2
5
9
78 9
5
6
2
4
2
9
6
100 9
5
Agrupe os dados em classes de freqüências.
7)Medindo-se o diâmetro externo de uma engrenagem, foram obtido
valores, em mm, de acordo com a seguinte distribuição:
Classes Frequências
1001 |— 1010
1011 |— 1020
1021 |— 1030
1031|— 1040
1041 |— 1050
1051 |— 1060
1061 |— 1070
1071 |— 1080
Total
3
12
28
82
74
30
17
4
250
Calcule a média e o desvio padrão desse lote de peças.
182

8)Uma amostra de chapas produzidas por uma máquina forneceu as
seguintes espessuras, em milímetros:
6,34 6,38 6,40 6,30 6,36 6,35
6,38 6,20 6,42 6,28 6,38
Há razões estatísticas para se afirmar que a distribuição das espessuras
seja simétrica?
9) Dada à distribuição de freqüências que segue, determine a mediana e
a proporção de elementos maiores que 4, supondo:
a. variável discreta;
b. variável contínua.
Xi fi
1
2
3
4
5
6
7
8
2
4
9
12
10
8
4
1
Total 50
O coeficiente de variação será o mesmo nos casos a) e b)? Por quê?
10)Uma amostra de oitenta peças retiradas de um grande lote forneceu a
183

seguinte distribuição de comprimentos:
Classes Frequências
50 |— 60 1
60 |— 70 3
70 |— 80 6
80 |— 90 15
90 |— 100 25
100 |— 110 20
110 |— 120 7
120 |— 130 3
Total 80
A especificação para esse tipo de material exige que o comprimento
médio das peças esteja compreendido entre 92 e 96 mm, que o coeficiente de
variação seja inferior a 20% e que a distribuição dos comprimentos seja
simétrica. Quais dessas exigências parecem não estar sendo satisfeita no
presente caso?
11) Uma distribuição de frequência é constituída por cinco classes de
igual amplitude cujas freqüências percentuais são, respectivamente ,
20%; 37,5%; 10,0% e 2,5%, o limite inferior da primeira classe é igual 2,
igual ao intervalo de classe da distribuição, e a frequência total é 200.
Calcule o índice de assimetria de PEARSON.
12) Numa região, para as distribuições de temperaturas e pressões
observadas durante um ano. Obtiveram-se respectivamente: temperatura
média 25º C; desvio padrão 2,5º C; pressão média 750 mm e desvio-
padrão 30 mm. Pergunta-se: qual a variável que apresentou maior
variabilidade naquele ano?
13) A distribuição abaixo resultou da determinação em cm dos diâmetros
de 200 arruelas fabricadas por determinada indústria de autopeças:
Classes Fi
5,3 – 5,32 12
184

5,32 – 5,34 22
5,34 – 5,36 44
5,36 – 5,38 60
5,38 – 5,40 42
5,40 – 5,42 20
Total 200
Pede-se:
a) Calcular a média e desvio padrão;
b) Determinar o valor do diâmetro tal que 12% dos valores da distribuição
lhe sejam inferior;
c) Determinar a porcentagem de valores superior a 5,39 cm.
14) O intervalo de tolerância para o comprimento de certa peça é de 5,40
± 0,25 cm. Examinando-se 50 dessas peças obteve-se a distribuição
abaixo:
Comprimentos Fi
4,995 – 5,195
5,195 – 5,395
5,395 – 5,595
5,595 – 5,795
8
20
16
6
Total 50
185

Pede-se:
a) Calcular a média e desvio-padrão da distribuição dada;
b) Calcular a percentagem de peças defeituosas nas 50 peças
examinadas;
c) Calcular a amplitude total da distribuição.
15) Numa caldeira foram realizadas 100 observações relativas à produção
de vapor/hora, tendo-se obtida para uma Equipe I de operadores a
distribuição de frequência I. Em idênticas condições operou uma Equipe
II. Os valores de X são os valores centrais da produção em toneladas de
vapor por hora.
I
Xi Fi
32,1 12
33,1 21
34,1 40
35,1 18
36,1 9
TOTAL 100
II
Xi Fi
32,2 9
33,2 19
34,2 38
35,2 22
36,2 12
TOTAL 100
Pede-se:
a) Comparar a eficiência da média e a regularidade na produção de vapor
pelas duas equipes;
b) Foi estabelecido para remuneração das equipes a condição de que a
186

frequência dos valores de X inferiores a 33,3 ton.?h seja no máximo de
25%. Verificar se esta condição é satisfeita pelas equipes e explique o
porquê.
16)A distribuição de freqüência abaixo resultou da medida (em cm) dos
diâmetros de esferas de um lote de 100 esferas de rolamento(precisão do
instrumento de 0,01 mm), cada uma das quais será utilizada em
determinado mecanismo.
Lote A
Classes Fi
14,845├─ 15,145 15
15,145├─ 15,445 20
15,445├─ 15,745 35
15,745├─ 16,045 22
16,045├─ 16,345 8
Total 100
Pergunta-se:
a)Qual será a porcentagem de mecanismos precisos, assim sendo
considerados aqueles para os quais os diâmetros das esferas estão no
intervalo de 15,30 a 15,7 mm?
b)Se é preferível utilizar esse lote(Lote A) ou outro para o qual:
_
X = 15,6 e S=0,40?
17)Abaixo estão descritos os parâmetros característicos de três
distribuições de frequência de três variáveis de interesse do engenheiro
na construção civil em 100 observações cada uma.
Distribuição I: Distribuição II: Distribuição III:
X1 = 10 X2 = 15 X3 = 25
S1 = 2 S2 = 2,5 S3 =10
Me1 = 10 Me2 = 15 Me3= 20
187

M01 = 10 M02 = 15 M03= 20
As1 = 0 As2 = 0 As3 = 0,5
K1 = 3,5 K2 = 3 K3= 3
Qual das distribuições acima possui “Curva Normal Padrão”? Justifique.
18)A distribuição abaixo representa o crescimento médio da eficácia de
certo medicamento por revisões em dez anos de seu composto químico.
x = 5%
S = 0,25%
Σ(x – x)2
= 300
Mo = 3,5%
Podemos modelar essa distribuição como a “Curva Normal”?
188

19)Os pesos de 1000 peças produzidas por certa indústria estão
classificados na tabela abaixo:
Pesos(em gramas) Nº de Peças
1900 │─── 1930 8
1930 │─── 1960 55
1960 │─── 1990 192
1990 │─── 2020 332
2020 │─── 2050 275
2050 │─── 2080 114
2080 │─── 2110 24
Total 1000
Calcule:
a)A mediana
b)1º e 3º quartil
c)Através das separatrises dos itens anteriores, inferir o grau de
assimetria e curtose.
189

20) Os dados mostrados a seguir referem-se às estaturas de 76 barras de
concreto para a construção civil:
1,7
2
1,6
4
1,5
5
1,6
3
1,5
4
1,7
2
1,5
2
1,8
4
1,8
5
1,80
1,67
1,80
1,68
1,65
1,76
1,80
1,66
1,69
1,74
1,74
1,76
1,65
1,70
1,72
1,68
1,77
1,79
1,82
1,69
1,71
1,83
1,68
1,74
1,50
1,67
1,92
1,76
1,55
1,79
1,89
1,69
1,73
1,66
1,66
1,67
1,55
1,67
1,78
1,80
1,65
1,78
1,73
1,60
1,56
1,73
1,64
1,74
1,65
1,78
1,60
1,62
1,63
1,80
1,72
1,75
,163
1,68
1,80
1,62
1,69
1,72
1,64
1,91
1,81
1,81
1,86
Realizar os principais estudos descritivos do conjunto de dados acima
utilizando somente a planilha eletrônica Excel.
21) Responda as questões abaixo:
a)Quais as técnicas aritméticas da Estatística Descritiva que informam a
forma de uma distribuição de frequência?
b)Como você descreveria o nível geral médio do tipo de camisa preferida
pelo mercado?
c)O que há de comum entre os objetivos das técnicas dos gráficos
estatísticos e das medidas de tendência central? Qual o ponto de
divergência?
d)Suponha que tenhamos gêneros alimentícios de indústrias de Niterói.
Que gráfico melhor se prestaria para informar instantaneamente o
comportamento proporcional dos diversos itens observados?
190

e)Qual o objetivo geral da Estatística Descritiva?
f)Qual o objetivo geral da Inferência Estatística?
g)Quais as duas formas de se fazer inferência?
h)Qual a diferença entre a estimação e os testes de hipóteses?
i)Qual a semelhança entre a estimação e os testes de hipóteses?
j)Qual é a técnica de estimação que oferece um conjunto de estimativas
para o parâmetro populacional, com uma confiança muito alta de estar
correta na atribuição?
22)A amostra abaixo se refere ao grau de satisfação de funcionários de
uma empresa com salário percebido e emprego, numa escala de 1 a 5.
Teste a normalidade das variáveis por Bera-Jarque.
Grau de Satisfação de Funcionários com Salário e Emprego
X(Salário) Y(Emprego)
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
1 1
2 1
2 2
2 2
2 2
2 2
3 3
4 4
4 4
5 5
191

Unidade IX
Números-Índices
Conceitos de Números-Índices:
o É uma medida estatística que compara o resultado de uma
variável em um período, chamado atual, com o resultado da
mesma variável em outra época chamada base;
o É a relação entre dois estados de uma variável, suscetível de
variar no tempo e no espaço;
o Representa o nível de um fenômeno em relação ao nível que ele
tinha num dado período tomado como base.
Índices mais Utilizados:
o Preço;
o Quantidade;
o Valor.
Número-índice Simples ou Relativos:
É o índice que representa uma comparação de um único bem.
Exemplo:
O índice de preços para a manteiga, de digamos 130, é um índice
simples e indica que o preço da manteiga aumentou 30% no período de
referência.
192

Fórmula Geral:
 Índice de Preço:

Onde:
Ip, índice de preços
Pt, preço do bem na época atual
Po, preço do produto na época base
 Índice de Quantidade:
Onde:
Iq, índice de quantidade
qt, quantidade do bem na época atual
qo, quantidade do produto na época base
Ip = Pt x 100%
Po
Iq = qt x 100%
qo
193

 Índice de Valor:
Exemplos:
1. Sabendo que o preço de uma pasta de executivo era de R$ 50,00 em
2000 e de R$ 60,00 em 2001, determine o índice simples de preço em
2001, tomando como base o ano de 2000 (2000=100).
Solução:
Ip = 60 x 100% = 120%
50
À nível relativo, este número significa que o preço da maleta era
100 em 2000 e passou a 120 em 2001, isto é, aumentou.
Variação Δ) = número-índice-100%
Logo, Δ= 120 – 100 = 20%
Conclusão:
O preço da maleta de executivo aumentou 20% de 2000 a 2001.
Iv = (pt x qt) x 100%
(po x qo)
194

2. Uma loja vendeu 45 meias em 1999 e 68 em 2000. Qual o índice
simples de quantidade tomando 1999 como ano base?
Solução:
Iq = 68 x 100% = 151%
45
Δ = 151 – 100 = 51%
Conclusão:
A quantidade aumentou em 51% no período.
3. Uma empresa vendeu, em 1997, 1000 unidades de um artigo ao preço
de R$ 500,00. Em 1998, vendeu 2000 unidades do mesmo produto ao
preço de R$ 600,00. Qual o relativo de valor tomando 1997 como ano
base?
Solução:
Iv = (600 x2000) x 100% = 240%
(500 x 1000)
Conclusão:
Em 1998, o valor das vendas foi 140% maior ao de 1997.
195

Relativos de Base Móvel (Elos Relativos):
Vários relativos formam elos quando cada um deles é calculado
tomando como base o ano anterior. São os relativos de base móvel.
Exemplo:
Anos Preços Elos Relativos
2001 240 ———
2002 300 125
2003 360 120
2004 540 150
P01,02 = (P02/P01) x100 = (300/240) x 100 = 1,25 x 100 = 125
P02,03 = (P03/P02) x 100 = (360/300) x 100 = 1,20 x 100 = 120
P03,04 = (P04/P03) x 100 = (540/360) x 100 = 1,50 x 100 = 150
196

Relativos de Base Fixa (Relativos em Cadeia):
O relativo em cadeia é o índice de base fixa: todos os relativos são
calculados tomando-se uma determinada época como base.
Exemplo:
Utilizando como exemplo os dados do item anterior e considerando 2001
como ano-base, obtemos:
Anos Preços Relativos em Cadeia
2001 240 100
2002 300 125
2003 360 150
2004 540 225
P01,01 = (P01/P01) x100 = (240/240) x 100 = 1,00 x 100 = 100
P01,02 = (P02/P01) x100 = (300/240) x 100 = 1,25 x 100 = 125
P01,03 = (P03/P01) x 100 = (360/240) x 100 = 1,50 x 100 = 150
P01,04 = (P04/P01) x 100 = (540/240) x 100 = 2,25 x 100 = 225
Fazemos uso dos relativos em cadeia quando se deseja comparar um
determinado ano, considerado significativo, com os anos anteriores e os
consecutivos.
197

Número-Índice Agregado ou Número-índice Composto:
É o índice que representa uma comparação de conjunto de bens.
Exemplo:
O IPC, Índice de Preços ao Consumidor, é um número-índice agregado,
e um IPC de 130, indica que o preço médio de uma cesta de mercado, com
certo número de bens e serviços foi 30% maior, comparativamente ao período
base. Mede o custo de vida.
Outros Exemplos:
o ICB, índice de cesta básica;
o IGP, índice geral de preços;
o IPC da FIPE;
o INPC, índice nacional de preços ao consumidor amplo;
198

Número-Índice Agregativo Simples:
É a média aritmética dos números índices simples de um conjunto de
itens considerados. É o índice médio de relativos.
Exemplo:
Tomando 2000 como ano base e 2001 como atual, tem-se a seguir os
seguintes relativos de preço dos seguintes produtos:
Bens Índice de Preços
Pão 115
Café 120
Leite 110
Manteiga 135
Total 480
O índice agregativo simples de preço será:
Igsp = 480 / 4 = 120%
Conclusão:
O conjunto de bens considerados aumentou cerca de 20%
199

Número-Índice Agregativo Ponderado
A ponderação proposta nestes índices baseia-se na participação de
cada bem no valor total e é feita, em geral, segundo dois critérios:
 Peso fixo na época básica;
 Peso variável na época atual.
1º)Número-Índice de Laspeyres ou Método da Época Básica:
No índice de Laspeyres, a base de ponderação é a época básica, daí a
denominação método da época básica.
a) Número-Índice de Laspeyres de Preços (Lp):
O índice de Laspeyres de preços é definido pela expressão:
Onde ‘t’ é o ano atual e ‘0’ é a época básica.
b) Número-Índice de Laspeyres de Quantidade (Lq):
O índice de quantidade, pelo método da época básica, é obtido pela
fórmula:
Lp0,t = Σ (pt x qo) . 100%
Σ(po x qo)
Lq0,t = Σ(qt x po) . 100%
Σ (qo x po)
200

Onde ‘t’ é o ano atual e ‘0’ é a época básica.
Exemplo:
Produtos 1992 1993 1994
Preço Qte Preço Qte Preço Qte
A 3 2 2 3 2 3
B 4 1 5 2 5 2
C 6 4 7 4,5 8 5
• Calcular o Índice de Laspeyres de Preço do ano de 1994, tendo
1992 como base:
Então:
Lp92,94 = Σ(p94 x q92) . 100% = (2x2)+(5x1)+(8x4) = 4+5+32 = 41/34
Σ(p92 x q92) (3x2)+(4x1)+(6x4) 6+4+24
= 1,21 x 100% = 121%
Conclusão:
O conjunto de bens considerados aumentou de preços cerca de 21% de
1992 a 1994.
• Calcular o Índice de Laspeyres de Quantidade do ano de 1994,
tendo 1992 como base:
Lq92,94 = Σ(q94 x p92) . 100% = (3x3)+(2x4)+(5x6) = 9+8+30
Σ(q92 x p92) (2x3)+(1x4)+(4x6) 6+4+24
=47/34 = 1,382 x 100% = 138,2.
201

Conclusão:
O conjunto de bens considerados aumentou de quantidade cerca de
38,2% de 1992 a 1994.
2º) Número-Índice de Paasche ou Método da Época Atual:
No índice de Passche, a base de pondera, a base de ponderação é a
época atual, daí a denominação método da época atual.
a) Número-Índice de Paashe de Preços (Pp):
É definido pela expressão:
Onde ‘t’ é a época atual e ‘0’ é a época base.
b) Número-Índice de Paashe de Quantidade (Pq):
É definido pela expressão:
Onde ‘t’ é a época atual e ‘0’ é a época base.
Pp0,t = Σ(pt x qt) . 100%
Σ (po x qt)
Pq0,t = Σ(qt x pt) . 100%
Σ (qo x pt)
202

• Do exemplo anterior, calcular o Índice de Passche de Preço do
ano de 1994, tendo 1992 como base:
Pp92,94 = Σ(p94 x q94) . 100% = (2x3)+(5x2)+(8x5) = 6+10+40 =
Σ(p92 x q94) (3x3)+(4x2)+(6x5) 9+8+30
56/47 = 1,191 x 100% = 119,1%
Conclusão:
O conjunto de bens considerados aumentou de preços cerca de 19,1%
de 1992 a 1994.
Calcular o Índice de Paasche de Quantidade do ano de 1994, tendo
1992 como base:
Pq92,94 = Σ(q94 x p94) . 100% = (3x4)+(2x4)+(5x8) = 12+10+40 =
Σ(q92 x p94) (2x4)+(1x5)+(4x8) 8+5+32
62/45 = 1,378 x 100% = 137,8%
Conclusão:
37,8% de 1992 a 1994.
203

3º) Número-Índice de Fischer ou Índice Ideal:
Este índice é obtido pela raiz quadrada dos respectivos índices de
Laspeyres e Paasche.
a) Número-Índice de Fischer de Preços (Fp):
b) Número-Índice de Fischer de Quantidade (Fq):
Onde:
Lp→Índice de Preço de Laspeyres
Pp→Índice de Preço de Paasche
Lq→Índice de Quantidade de Laspeyres
Pq→Índice de Quantidade de Paasche
Fp0,t = √Lp x Pp
Fq0,t = √Lq x Pq
204

Exemplo:
Considere os índices dos exemplos anteriores:
 Calcular o Índice de Fischer de Preço:
Fp92,94 = √Lp92,94 x Pp92,94 = √1,21 x 1,191 = 120,0%.
Conclusão:
O conjunto de bens considerados aumentou de preços cerca de 26,3%
de 1992 a 1994.
 Calcular o Índice de Fischer de Quantidade:
Fq92,94 = √Lq92,94 x Pq92,94 = √1,382 x 1,378= 1,380 = 138,0%
Conclusão:
38,0% de 1992 a 1994.
205

Construção de Índices de Preços
Para construir um índice de preços, qualquer que seja a sua finalidade
devemos inicialmente considerar os seguintes pontos:
a. Qual o objetivo do índice?
b. Que produtos devem ser incluídos no seu cálculo?
c. Quais os preços a serem incluídos no seu cálculo?
d. Qual o peso a ser atribuído a cada bem em particular?
e. Qual a fórmula adequada?
Embora não tendo uma resposta imediata para as questões acima,
alguns pontos básicos devem ser observados sempre que pretendemos
construir qualquer índice.
a. Objetivo do índice
É fundamental qualificar, com toda a precisão, o objetivo do índice;
determinar o que ele está medindo e a quem se refere. Dessa determinação
dependerá a seleção dos produtos que comporão o índice.
b. Produtos a serem incluídos
Devem ser incluídos os produtos julgados mais importantes e que sejam
representativos do conjunto de bens que integram o setor para o qual se vai
calcular o índice.
206

c. Preços a serem incluídos
Deve-se identificar o setor para o qual vão ser determinados os preços
(varejo, atacado etc.). Também é necessário decidir a forma de cotação e
como deverão ser coletados os preços.
d. Pesos a serem atribuídos
O sistema de pesos a ser atribuído deve depender essencialmente da
finalidade ou da utilidade do índice. Os pesos, por isso mesmo, devem refletir a
importância relativa de cada bem no conjunto tomado para a determinação do
índice.
e. Fórmula
Em geral, quando se trata de índices de preços, é usada a fórmula de
Laspeyres, que emprega pesos fixos, permitindo a revisão periódica de seus
valores. Resulta daí a possibilidade de termos sempre as mesmas
comparações, feitas diretamente ou através de elos de relativos.
207

Taxas de Inflação
Toda análise econômica utiliza-se de dados numéricos e estatísticos,
para viabilizar o desenho de cenários. Quando se trata de análise
macroeconômica, é importante que sempre seja considerada a inflação,
pois seus efeitos, de acordo com a teoria econômica, são muito mais
intensos sobre a demanda agregada, do qualquer outra variável. Dada à
importância de tal indicador, é colocado neste livro uma visão estrutural e
conceitual da inflação. Aborda-se também um levantamento sobre os
índices de preços calculados pelos principais institutos de estatística no
Brasil e, por conseguinte aborda algumas aplicações práticas dos índices
apresentados e divulgados à população.
Os índices de inflação são utilizados para avaliar a variação de
preços num determinado setor da economia. Explicando melhor, inflação é
o aumento contínuo no nível geral de preços, ocasionando uma perda do
poder aquisitivo da moeda, assim os índices de inflação “medem” o quanto
variam esses preços, para baixo ou para cima. Os índices de preços, vários
como são dentro da economia, pretendem verificar a variação monetária ou
taxa inflacionária sempre em um período de tempo.
Pelas suas características específicas, complexidade e gigantismo
geográfico, pode-se verificar, num país com dimensões continentais como o
Brasil, com tantas diferenças e peculiaridades regionais, que a tarefa de
medir a inflação é das mais difíceis.
Os institutos que calculam os índices não apuram resultados com
diferenças significativas entre si, isso tudo apesar das peculiaridades
regionais e metodológicas. Ao contrário do que dizem as pessoas
desinformadas, mostra que os índices não são manipulados, se a conclusão
fosse essa, dir-se-ia que todos eles o são, pois os resultados são muito
parecidos.
208

Não cabe neste momento explicar as razões econômicas das
variações, mas apresentar a relação entre os índices, que mesmo
tratando-se de metodologias de cálculo e de populações diferentes
apresentam uma semelhança em seus valores.
Os principais índices econômicos, ou mais aceitos, são os
medidos pelas seguintes entidades: Instituto Brasileiro de Geografia e
Estatística(IBGE), Universidade de São Paulo(FIPE), Fundação Getúlio
Vargas (FGV) e DIEESE.
Taxa de Inflação:
A metodologia de cálculo ou medição de inflação é muito sofisticada.
Os índices refletem a variação de milhares de preços. O índice de inflação
é uma média ponderada de uma "cesta" de consumo de um
determinado segmento da sociedade(construção civil, produção
industrial,serviços de telecomunicações, etc),ou da renda familiar (famílias
que ganham até 3 salários mínimos, por exemplo).
Vejamos um exemplo muito simples e vamos aplicá-lo para um
índice que reflita os preços do dia 1 ao 30 de um mês.
209

1º passo:
È necessário determinar o público ou setor da economia do qual
desejamos medir a inflação, como se pode verificar no quadro abaixo cada
índice representa a medida da perda de poder aquisitivo de um setor ou
de famílias com determinados níveis de renda.
Quadro
Público Índice
Índice Público ou Setor que tem a Variação de Preços Medidas
SINDUSCOM Setor da construção civil
IPC-FIPE Famílias com renda entre 1 e 30 salários mínimos
IPCA-IBGE Famílias com renda entre 1 e 44 salários mínimos
IGP-M Mede a inflação da economia de modo geral,
representado pela ponderação de três outros índices: IPA que mede os
preços no atacado, INCC que mede a variação dos preços na área da
construção civil e IPC que mede a variação de preços ao consumidor para
famílias com renda de até 30 salários mínimos.
Pelo quadro acima, pode-se concluir que em linhas gerais o IPC-
FIPE e o IPCA, devem produzir resultados bastante parecidos.
Entretanto, o IGP-M, em certas circunstâncias, poderá apresentar
variações muito diferentes, haja vista, o mesmo incluir a medida de
variação de preços no atacado, por exemplo, fato não abrangido pelos
demais, pelo menos na mesma forma.
210

2º passo:
Uma pesquisa de campo irá determinar uma "cesta" de itens
consumidos que melhor represente os “gastos” daquela família ou setor, ou
seja, do público alvo. Suponha, para fins desse exemplo, tratar-se de uma
família com renda entre X e Y salários mínimos. Após uma pesquisa
descobrimos o que essa família consome mensalmente, ou seja,
determinamos a sua “cesta de consumo”, hipoteticamente representada
apenas por cinco itens do quadro a seguir. Essa cesta imaginária,
composta por apenas 5 (cinco) itens – representa todo o consumo da
família selecionada. No caso do IPCA - IBGE são cerca de 250.000
itens de consumo e os dados são levantados segundo uma complexa
e cara pesquisa chamada de POF (Pesquisa de Orçamento Familiar).
Quadro
Cesta de Consumo
Item
Luz
Água
Telefone
Gasolina
Feijão
211

Observação:
As famílias, quanto à renda, têm padrão de consumo diferente.
Para o DIEESE, cuja cesta de consumo abrange famílias que ganham até
30 salários mínimos, os produtos consumidos, e conseqüentemente a
inflação, poderá ser muito diferente do consumo das famílias do IPCA
amplo, cuja renda é de até 44 salários mínimos. O presente exemplo
contém ilustrações forçadas, assim, ao invés de colocar um item
chamado “ALIMENTAÇÃO”, com milhares de itens, simplificamos para fins
didáticos apenas pelo item “FEIJÃO”, pois é mais mensurável e fácil de
entender, mas, o leitor por certo saberá que uma família, ao certo, não
consumirá apenas “FEIJÃO”.
A composição dos grupos de despesas para o cálculo do IPCA, por
exemplo, é o seguinte: Alimentação, Artigos de Residência, Habitação,
Transportes e Comunicação, Vestuário, Saúde, Cuidados e Despesas
Pessoais.
O quadro abaixo mostra quanto cada um desses grupos de
despesas representa percentualmente dentro da cesta de consumo.
Cesta de Consumo do IPCA
Grupos de Despesas da Cesta Percentual(%)
Alimentação 25,1
Artigos de Residência 8,09
Habitação 10,91
Transporte e Comunicação 18,77
Vestuário 12,49
Saúde e Cuidados Especiais 8,85
Despesas pessoais 15,68
Vale lembrar que cada um dos grupos de despesas
representados no quadro acima, por sua vez, é composto por subgrupos e
esses, também por sua vez, abre-se em milhares de itens.
212

3º Passo:
Uma vez determinado o público alvo, bem como seus respectivos
itens de consumo, resta agora, determinar as quantidades consumidas
pela nossa família fictícia, para cada um dos cinco itens apontados na cesta
de consumo, também fictícia. O quadro a seguir indica este resultado.
Cesta de Consumo do IPCA
Item Quantidade
Luz 100 kWh
Água 20 m3
Telefone 100 pulsos
Gasolina 20 litros
Feijão 5 kilogramas
213

4º passo:
Neste passo, já se inicia a fase operacional do índice, com o
começo da medida semanal dos preços, pois, depois de determinada
a "cesta" e as quantidades consumidas, é preciso quantificá-la em valor.
Essa operação será feita no primeiro (1º) dia do mês, multiplicando-
se as quantidades de cada um dos itens consumidos pela família
hipotética, pelo seu respectivo preço de mercado, refletindo no
quadro apresentado abaixo o valor da cesta de consumo, ou seja, R$
100,00.
Valor da Cesta de Consumo no Primeiro Dia do Mês
Item Quantidade Valor
Unitário(R$)
Total(R$)
Luz 100 kWh 0,20 20,00
Água 20 m3
0,50 10,00
Telefone 100 pulsos 0,10 10,00
Gasolina 20 litros 1,00 20,0
Feijão 5 kilogramas 8,00 40,00
Total ── ── 100,00
214

5º Passo:
Finalmente, já se pode fazer o primeiro registro da variação dos
preços, os quais no Brasil quase invariavelmente são para maior. Desse
modo, tendo definido uma "cesta", os itens e as respectivas quantidades
consumidas pela “família”, e sabendo também quanto ela vale no primeiro
dia do mês, é necessário medi-la novamente, agora no último dia do mês,
conforme mostra quadro a seguir.
Valor da Cesta de Consumo no Último Dia do Mês
Unitário(R$)
Total(R$)
Luz 100 kWh 0,24 24,00
Água 20 m3
0,65 13,00
Total ── ── 115,00
Como podemos observar pelo cálculo abaixo, no último dia
do mês os preços coletados haviam mudado a "cesta" agora
passou a custar $ 115, neste caso, experimentou-se uma inflação de
15% no mês:
IP = (115/100) x 100 = 115% → ∆ = 15%
215

Inflação Quadrissemanal:
Na prática, os institutos como o IBGE, a FIPE ou a FGV
comparam as médias aritméticas dos preços das quatro semanas de
um mês com as do mês anterior de cada cesta. A variação (∆) é a
inflação quadrissemanal. No nosso exemplo, a "cesta" de consumo
apresentou nas semanas de quatro meses analisados quatro
diferentes valores que representam a sua média quadrissemanal: R$
122,50, R$ 148,75, R$ 153,50 e R$155,00, respectivamente.
Semanas Preços de
Janeiro
Preços de
Fevereiro
Preços de
Março
Preços
de Abril
1ª 100 146 152 155
2ª 115 148 153 155
3ª 130 149 154 155
4ª 145 152 155 155
Média 122,5 148,75 153,50 155
Inflação ─── 21,43% 3,19% 0,98%
Pelo quadro acima, comparando-se as médias, obtém-se a inflação
do mês, ou seja, a média de abril no valor de R$ 155, 00,quando
comparada com a média de março no valor de R$ 153,50, mostra uma
variação nos preços de 0,98%.
Cálculo da Taxa de Inflação
Meses Cálculo da Inflação
Fevereiro (148,75 / 122,50) = 21,43%
Março (153.50 / 148,75) = 3,19%
Abril (155.00 / 153,50) = 0,98%
Pelos cálculos mostrados nos quadros acima, se verificou que
muito embora os preços não tenham mais subido a partir da terceira
s e m a n a de março, por força da metodologia, a inflação de abril,
mesmo assim, foi de 0,98 %.
216

Inflação Mensal Acumulada
Com o conceito do valor do dinheiro no tempo, podemos
retirar várias aplicações práticas, como por exemplo, o cálculo da inflação
mensal acumulada, como ferramenta para diversas aplicações de
atualização, correção e análise de valores.
Exemplo:
Índice de Inflação Mensal Acumulada
Meses Inflação(%) ∆AC
Janeiro 1,4 1,4
Fevereiro 2,5 3,9
Março 2,9 6,8
Abril 1,8 8,6
Maio 1,0 9,6
Junho 1,9 11,5
217

Número- Índice Mensal Acumulado
A variação acumulada é uma informação importante, mas
para dar-lhe um caráter mais prático, seria muito útil construir
também um índice com as variações mensais, cujo valor alcança
111,5 em junho.
Número-Índice Acumulado com Base em Dezembro= 100
Meses Inflação(%) ∆AC NIAC
Janeiro 1,4 1,4 101,4
Fevereiro 2,5 3,9 103,9
Março 2,9 6,8 106,8
Abril 1,8 8,6 108,6
Maio 1,0 9,6 109,6
Junho 1,9 11,5 111,5
218

Indicadores de Inflação:
Os índices de inflação são usados para medir a variação dos
preços e o impacto no custo de vida da população.
Cada um tem uma metodologia diferente, e a medição é feita
por diversos órgãos especializados, como o IBGE (Instituto
Brasileiro de Geografia e Estatística), a FGV(Fundação Getúlio
Vargas) e a FIPE (Fundação Instituto de Pesquisas
Econômicas).
Entre as diferenças de método, estão os dias em que os
índices são apurados, os produtos que incluem, o peso deles na
composição geral e a faixa de população estudada.
O IPCA (Índice Nacional de Preços ao Consumidor Amplo),
por exemplo, considerado a inflação oficial do país, é medido pelo
IBGE entre os dias 1º e 30 de cada mês.
Ele considera gastos como alimentação e bebidas; artigos de
residência; comunicação; despesas pessoais; educação; habitação;
saúde e cuidados pessoais.
O indicador reflete o custo de vida de famílias com renda
mensal de 1 a 44 salários mínimos.
Outro exemplo é o IGP-M (Índice Geral de Preços do
Mercado), monitorado pela FGV. Ele registra a inflação de preços
variados, desde matérias-primas agrícolas e industriais até bens e
serviços finais. É muito usado na correção de aluguéis e tarifas
públicas, como conta de luz. Serve para todas as faixas de renda.
A seguir serão definidos os principais indicadores de inflação
no país.
219

1) INPC
O INPC (Índice Nacional de Preços ao Consumidor) é medido
pelo IBGE (Instituto Brasileiro de Geografia e Estatística) desde
setembro de 1979. Ele é obtido a partir dos Índices de Preços ao
Consumidor regionais e tem como objetivo oferecer a variação dos
preços no mercado varejista, mostrando, assim, o aumento do custo
de vida da população.
Como o INPC mede uma faixa salarial mais baixa que o IPCA
(até 6 salários mínimos, diante dos 44 salários mínimos do IPCA), a
alteração de preços de serviços e produtos mais básicos é mais
sentida neste índice. O peso do grupo alimentos (arroz, feijão, leite,
frutas, refeições feitas em restaurantes, lanchonetes) é maior no
INPC que no IPCA. Logo, uma variação nesse grupo tem um
impacto maior no INPC.
Por exemplo, se a cesta básica passar de R$ 100,00 para R$
150,00, uma família que tenha renda de um salário mínimo sentirá
muito mais esse aumento que uma com renda de nove salários
mínimos.
Além disso, o gás de cozinha (dentro do grupo habitação) e o
preço das passagens de ônibus (dentro do grupo transporte)
também têm maior peso no INPC. Já os aumentos ou quedas nos
preços de automóveis e da gasolina têm maior peso no IPCA,
porque não são itens de consumo tão importante nas faixas de
menor renda.
220

Como é calculado o INPC?
O período de coleta do INPC vai do dia 1º ao dia 30 ou 31,
dependendo do mês. A pesquisa é realizada em estabelecimentos
comerciais, prestadores de serviços, domicílios (para verificar
valores de aluguel) e concessionárias de serviços públicos. Os
preços obtidos são os efetivamente cobrados ao consumidor, para
pagamento à vista.
São considerados nove grupos de produtos e serviços:
alimentação e bebidas; artigos de residência; comunicação;
despesas pessoais; educação; habitação; saúde e cuidados
pessoais; transportes e vestuário. Eles são subdivididos em outros
itens. Ao todo, são consideradas as variações de preços de 250.000
itens.
O INPC mede a inflação para que parcela da população?
Abrange famílias com rendimentos mensais entre 1 e 6
salários mínimos, residentes nas regiões metropolitanas de São
Paulo, Rio de Janeiro, Belo Horizonte, Porto Alegre, Curitiba,
Salvador, Recife, Fortaleza e Belém, além do Distrito Federal e do
município de Goiânia.
Para que é usado o INPC?
O índice é utilizado para negociação de reajustes salariais:
atualmente é componente para o cálculo do reajuste do salário
mínimo: variação do Produto Interno Bruto(PIB) de dois anos
anteriores somada à inflação registrada pelo INPC.
221

2) IPCA
O IPCA (Índice de Preços ao Consumidor Amplo), medido
mensalmente pelo IBGE (Instituto Brasileiro de Geografia e
Estatística), foi criado com o objetivo de oferecer a variação dos
preços no comércio para o público final. O IPCA é considerado o
índice oficial de inflação do país.
Como é calculado o IPCA?
O período de coleta do IPCA vai do dia 1º ao dia 30 ou 31,
dependendo do mês. A pesquisa é realizada em estabelecimentos
pagamento à vista.
itens.
O IPCA mede a inflação para que parcela da população?
O indicador reflete o custo de vida de famílias com renda
mensal de 1 a 44 salários mínimos, residentes nas regiões
metropolitanas de São Paulo, Rio de Janeiro, Belo Horizonte, Porto
Alegre, Curitiba, Salvador, Recife, Fortaleza e Belém, além do
Distrito Federal e do município de Goiânia.
222

Para que é usado o IPCA?
É utilizado pelo Banco Central como medidor oficial da
inflação do país. O governo usa o IPCA como referência para
verificar se a meta estabelecida para a inflação está sendo
cumprida.
3) IPCA-E
O IPCA-E (Índice Nacional de Preços ao Consumidor Amplo
Especial), medido pelo IBGE (Instituto Brasileiro de Geografia e
Estatística), segue a mesma metodologia de cálculo do IPCA, mas é
divulgado ao final de cada trimestre, sendo formado pelas taxas do
IPCA-15 de cada mês. A apuração do IPCA-E foi iniciada em 1991 e
seu objetivo é realizar um balanço trimestral da inflação.
Como é calculado o IPCA-E?
O período de coleta do IPCA-E vai do dia 16 do mês anterior
ao dia 15 do mês atual. A pesquisa é realizada em estabelecimentos
pagamento à vista.
itens.
223

O IPCA-E mede a inflação para que parcela da população?
Abrange famílias com rendimento mensal de 1 a 44 salários
mínimos, qualquer que seja a fonte de rendimentos, e residentes nas
áreas urbanas das regiões metropolitanas de São Paulo, Rio de
Janeiro, Belo Horizonte, Porto Alegre, Curitiba, Salvador, Recife,
Fortaleza e Belém, além do Distrito Federal e do município de
Goiânia.
Para que é usado o IPCA-E?
O índice é utilizado para reajustes de IPTU (Imposto Predial e
Territorial Urbano).
4) IPCA-15
O IPCA-15 (Índice de Preços ao Consumidor Amplo-15),
medido pelo IBGE (Instituto Brasileiro de Geografia e Estatística), foi
criado com o objetivo de oferecer a variação dos preços no mercado
varejista, mostrando, assim, o aumento do custo de vida da
população. Começou a ser divulgado a partir de maio de 2000.
O IPCA-15 é uma prévia do IPCA (Índice de Preços ao
Consumidor Amplo), o indicador oficial da inflação no país. Como
realiza a medição de preços em um período não calculado pelo
IPCA, mostra qual será a tendência do resultado do final do mês.
Além disso, o IBGE tem uma comparação mais precisa da alta e
queda dos preços, pois a cada 15 dias um dos índices é divulgado.
A coleta de dados para a medição do IPCA e do IPCA-15 é uma só.
O que muda é o período analisado em cada um dos itens.
224

Como é calculado o IPCA-15?
O período de coleta de preços, que acontece em
estabelecimentos comerciais e de prestação de serviços,
concessionárias de serviços públicos e domicílios (para
levantamento de aluguel e condomínio), vão do dia 16 do mês
anterior ao dia 15 do mês atual.
itens.
O IPCA-15 mede a inflação para que parcela da população?
Abrange famílias com rendimento mensal entre 1 e 44
salários mínimos, residentes nas regiões metropolitanas de São
Paulo, Rio de Janeiro, Belo Horizonte, Porto Alegre, Curitiba,
Salvador, Recife, Fortaleza e Belém, além do Distrito Federal e do
município de Goiânia.
Para que é usado o IPCA-15?
O índice é utilizado para reajustes de IPTU (Imposto Predial e
Territorial Urbano).
225

5) IGP
O Índice Geral de Preços (IGP), medido pela Fundação
Getúlio Vargas (FGV), registra a inflação de preços desde matérias-
primas agrícolas e industriais até bens e serviços finais. O IGP é
formado pela média de três índices que refletem a economia: IPA
(Índice de Preços por Atacado, com peso de 60%); IPC (Índice de
Preços ao Consumidor, peso de 30%); e INCC (Índice Nacional de
Custos da Construção, peso de 10%).
O IGP é divulgado em três versões: IGP-DI (Índice Geral de
Preços - Disponibilidade Interna); IGP-M (Índice Geral de Preços do
Mercado) e IGP-10 (Índice Geral de Preços 10). O que difere as três
versões é o período de pesquisa dos dados.
O IGP-DI faz medições no mês cheio, ou seja, do dia 1º ao
dia 30 ou 31 de cada mês. No IGP-M, o período vai do dia 21 do
mês anterior ao dia 20 do mês atual. O IGP-10 mede a evolução de
preços no período compreendido entre o dia 11 do mês passado e o
dia 10 do mês corrente.
Como é calculado o IGP?
Os IGPs são compostos pelos índices IPA, IPC e INCC.
Os dados do IPA são pesquisados nas capitais onde haja
indústrias.
O IPC é o cálculo da variação de preços de produtos e
serviços. A pesquisa é realizada em São Paulo, Rio de Janeiro, Belo
Horizonte, Porto Alegre, Salvador, Recife e Brasília. Esse índice é
formado por oito grupos: habitação (com itens como empregada
doméstica e material de limpeza), alimentação, transportes, saúde e
cuidados pessoais (remédios, planos de saúde e sabonete entre
outros), educação, leitura e recreação, vestuário e despesas
diversas (itens como cartório, loteria e mensalidade de Internet).
Os dados do INCC apresentam relatórios da construção civil.
As medições são feitas nas capitais São Paulo, Rio de Janeiro,
226

Curitiba, Belo Horizonte, Porto Alegre, Florianópolis, Salvador,
Recife, Fortaleza, Belém, Brasília e Goiânia. Esse índice contém três
grupos: materiais (azulejos, pisos e louças), serviços (aluguéis) e
mão-de-obra (pedreiros).
O IGP mede a inflação para que parcela da população?
Abrange toda a população, sem restrição de nível de renda.
Para que é usado o IGP?
Reajustes de tarifas públicas, contratos de aluguel e planos e
seguros de saúde (nos contratos mais antigos).
6) IGP-10
O IGP-10 (Índice Geral de Preços 10) é uma das versões do
Índice Geral de Preços (IGP). Medido pela Fundação Getúlio Vargas
(FGV), registra a inflação de preços desde matérias-primas agrícolas
e industriais até bens e serviços finais.
Como é calculado o IGP-10?
O IGP-10 mede a evolução de preços no período
compreendido entre o dia 11 do mês anterior e o dia 10 do mês
atual. Ele é formado por 60% do IPA-10 (Índice de Preços por
Atacado-10), 30% do IPC-10 (Índice de Preços ao Consumidor-10) e
10% do INCC-10 (Índice Nacional de Custos da Construção-10).
Esses indicadores medem itens como bens de consumo (um
exemplo é alimentação) e bens de produção (matérias-primas,
materiais de construção, entre outros). Entram, além de outros
componentes, os preços de legumes e frutas, bebidas e fumo,
remédios, embalagens, aluguel, condomínio, empregada doméstica,
transportes, educação, leitura e recreação, vestuário e despesas
227

diversas (cartório, loteria, correio, mensalidade de Internet e cigarro,
entre outros).
O IGP-10 mede a inflação para que parcela da população?
Para que é usado o IGP-10?
7) IGP-DI
O IGP-DI (Índice Geral de Preços - Disponibilidade Interna) é
uma das versões do Índice Geral de Preços (IGP). É medido pela
Fundação Getúlio Vargas (FGV) e registra a inflação de preços
desde matérias-primas agrícolas e industriais até bens e serviços
finais.
Como é calculado o IGP-DI?
O IGP-DI (Índice Geral de Preços - Disponibilidade Interna)
faz medições no mês cheio, de 1 a 30 ou 31 de cada mês. Ele é
formado pelo IPA-DI (Índice de Preços por Atacado - Disponibilidade
Interna), IPC-DI (Índice de Preços ao Consumidor - Disponibilidade
Interna) e INCC-DI (Índice Nacional do Custo da Construção -
Disponibilidade Interna), com pesos de 60%, 30% e 10%,
respectivamente. O período de coleta dos três é o mesmo do IGP-
DI.
228

Mais detalhes dos Componentes do IGP-DI:
o Índice de Preços no Atacado (IPA) - onde entram preços
praticados do mercado atacadista e representa 60 % do IGP-
DI.
o Índice de Preços ao Consumidor (IPC) - a coleta de dados
ocorre nas cidades de São Paulo e Rio de Janeiro dentre as
famílias que tem uma renda de 1 a 33 salários mínimos.
Representa 30 % do IGP-DI.
o Índice Nacional de Construção Civil (INCC) - onde são
avaliados os preços no setor de construção civil, não só de
materiais como de mão-de-obra. Representa 10 % do IGP-DI.
entre outros).
O IGP-DI mede a inflação para que parcela da população?
Para que é usado o IGP-DI?
229

8) IGP-M
O IGP-M (Índice Geral de Preços do Mercado) é uma das
versões do Índice Geral de Preços (IGP). É medido pela Fundação
Getúlio Vargas (FGV) e registra a inflação de preços desde
matérias-primas agrícolas e industriais até bens e serviços finais.
Como é calculado o IGP-M?
Esse índice é formado pelo IPA-M (Índice de Preços por
Atacado - Mercado), IPC-M (Índice de Preços ao Consumidor -
Mercado) e INCC-M (Índice Nacional do Custo da Construção -
Mercado), com pesos de 60%, 30% e 10%, respectivamente. A
pesquisa de preços é feita entre o dia 21 do mês anterior até o dia
20 do mês atual.
entre outros).
O IGP-M mede a inflação para que parcela da população?
Para que é usado o IGP-M?
Contratos de aluguel, reajustes de tarifas públicas e planos e
230

9) IPC-FIPE
O IPC-Fipe (Índice de Preços ao Consumidor, da Fundação Instituto de
Pesquisas Econômicas) começou a ser calculado em janeiro de 1939 pela
Divisão de Estatística e Documentação da Prefeitura de São Paulo, com o
nome de Índice Ponderado do Custo de Vida da Classe Operária na cidade de
São Paulo. Em 1968, a responsabilidade do cálculo passou para o Instituto de
Pesquisas Econômicas da USP e, posteriormente, em 1973, com a criação da
Fipe, para esta instituição. O nome atual do índice foi adotado em 1972. Ele
mede a inflação na cidade de São Paulo.
Como é calculado o IPC-Fipe?
O IPC-FIPE é calculado medindo-se o mês cheio, de 1 a 30 ou 31, e de
maneira quadrissemanal. O sistema de cálculo da variação quadrissemanal do
IPC-Fipe abrange um período de oito semanas de coleta. Em cada
quadrissemana, as variações são obtidas dividindo-se os preços médios das
quatro últimas semanas (referência) pelos preços médios das quatro semanas
anteriores a elas (base).
Para o cálculo da nova taxa, incluem-se os preços da última semana e
descartam-se os valores da semana mais antiga. Por exemplo, na primeira
quadrissemana de agosto, o período de referência (as quatro últimas
semanas), vai de 8 de julho a 7 de agosto. Já o período das quatro semanas
anteriores a estas (base) vai de 8 de junho a 7 de julho. O resultado da primeira
quadrissemana de agosto é obtido divindo-se os preços médios do período de
8 de julho a 7 de agosto pelos de 8 de junho a 7 de julho.
Na segunda quadrissemana de agosto, a referência é o período que vai de 16
julho a 15 de agosto. Ou seja, a primeira semana de julho foi retirada e a
segunda de agosto, acrescentada, mantendo-se um total de 8 semanas.
São consideradas as variações de preços de produtos e serviços
definidos por uma Pesquisa de Orçamentos Familiares (POF), que indica o que
231

cada família gasta em média e quais itens são de maior relevância. Além disso,
uma POF também tem como finalidade incorporar produtos e serviços novos.
Sete grupos de análise são utilizados pela Fipe (listados em ordem
decrescente de peso nos cálculos): habitação (32,79%), alimentação (22,73%),
transportes (16,03%), despesas pessoais (12,30%, com itens como fumo,
bebidas, recreação e artigos de higiene e beleza), saúde (7,08%), vestuário
(5,29%) e educação (3,78%).
O IPC-Fipe mede a inflação para que parcela da população?
O indicador reflete o custo de vida de famílias com renda mensal de 1 a
20 salários mínimos, residentes na cidade de São Paulo.
Para que é usado o IPC-Fipe?
O IPC-Fipe é utilizado como indexador informal para contratos da
Prefeitura de São Paulo.
10) IPC-S
O Índice de Preços ao Consumidor Semanal (IPC-S) calcula a variação
de preços de produtos e serviços em sete capitais do país. É medido pela
Fundação Getúlio Vargas (FGV) e teve seu início de apuração em 2003.
Como é calculado o IPC-S?
O IPC-S registra a evolução de preços de maneira quadrissemanal, com
fechamentos nos dias 7, 15, 22 e 30 de cada mês.
São sempre consideradas quatro semanas (por isso o nome
quadrissemana). Por exemplo, no fechamento do dia 7 do mês atual, o cálculo
é realizado com base nessa primeira semana e nas três últimas do mês
232

anterior. Já no fechamento do dia 15, o cálculo considera as duas últimas
semanas do anterior e as duas primeiras do atual.
São consideradas as variações de preços de 456 itens definidos por
meio de uma Pesquisa dos Orçamentos Familiares (POF), aplicada pela FGV,
em média, a cada quatro anos.
A POF indica o que cada família gasta em média e quais itens possuem
maior relevância. Além disso, também tem como finalidade incorporar produtos
e serviços novos.
Esses produtos e serviços são distribuídos em sete classes de despesas
(listadas, a seguir, pela ordem de peso no cálculo da pesquisa, da maior para a
menor): habitação (31,51%), alimentação (27,20%), transportes (12,76%),
saúde e cuidados pessoais (10,53%; inclui remédios e higiene pessoal),
educação, leitura e recreação (8,63%), vestuário (4,80%) e despesas diversas
(4,57%; inclui gastos como cartório, loteria, correio, mensalidade de Internet,
cigarro e outros).
O IPC-S mede a inflação para que parcela da população?
33 salários mínimos, residentes nas seguintes capitais: São Paulo, Rio de
Janeiro, Salvador, Belo Horizonte, Porto Alegre, Recife e Brasília.
11) IPC-SP
O IPC-SP (Índice de Preços ao Consumidor - São Paulo) calcula a
variação de preços de produtos e serviços da cidade de São Paulo. Ele
começou a ser medido em 1989 pela FGV (Fundação Getúlio Vargas).
Como é calculado o IPC-SP?
A partir de 2003, o IPC-SP passou a calcular a evolução de preços de
233

maneira quadrissemanal (antes o cálculo era semanal), com fechamentos nos
dias 7, 15, 22 e 30.
São sempre consideradas quatro semanas (por isso o nome
quadrissemana). Por exemplo, no fechamento do dia 7 do mês atual, o cálculo
é realizado com base nessa primeira semana e nas três últimas do mês
anterior. Já no fechamento do dia 15, o cálculo considera as duas últimas
semanas do mês anterior e as duas primeiras do atual.
São medidas as variações de preços de 456 itens definidos por meio de
uma Pesquisa dos Orçamentos Familiares (POF), aplicada pela FGV, em
média, a cada quatro anos.
A POF indica o que cada família gasta em média e quais itens têm maior
relevância. Além disso, também tem como finalidade incorporar produtos e
serviços novos.
Esses produtos e serviços são distribuídos em sete classes de despesas
(listadas, a seguir, pela ordem de peso no cálculo da pesquisa, da maior para a
menor): habitação (31,51%), alimentação (27,20%), transportes (12,76%),
saúde e cuidados pessoais (10,53%; incluem remédios e higiene pessoal,
educação, leitura e recreação (8,63%), vestuário (4,80%) e despesas diversas
(4,57%, incluem gastos como cartório, loteria, correio, mensalidade de Internet,
cigarro e outros).
O IPC-SP mede a inflação para que parcela da população?
33 salários mínimos, residentes na cidade de São Paulo.
Para que é usado o IPC-SP?
É usado para alimentar o IGP (Índice Geral de Preços), também da FGV,
que registra a inflação de preços desde matérias-primas agrícolas e industriais
até bens e serviços finais. Também serve de referência para reajustes salariais
234

e contratos de aluguéis.
Deflacionamento de Dados
Sabemos que os aumentos de preços implicam baixas no poder de
compra ou no valor da moeda. Por isso mesmo, a manutenção do poder de
compra dos salários é um problema que muito preocupa os assalariados de
países onde o valor da moeda está continuamente se deteriorando.
Assim, embora os salários nominais estejam frequentemente
aumentando , os salários reais podem estar diminuindo, devido ao aumento do
custo de vida (inflação), e, consequentemente, tendo o seu poder aquisitivo
reduzido.
Daí a importância dos índices de preços, pois a eles recorremos para
responder a questões como esta:
O deflacionamento trata da conversão de salários nominais em salários
reais, de importância fundamental na época das negociações salariais,
principalmente quando há inflação.
235

Para determinamos os salários reais (SR), também denominados salários
deflacionados, dividimos os salários nominais das várias épocas (St) pelo
índice de preços das épocas correspondentes (IPt) e multiplicamos o resultado
por 100:
(1)
Assim, se o salário de um professor, em dezembro de 1995, era de R$
1.071,00 e o IP de dezembro de 1995, com base em novembro, era de
101,24%, o valor desse professor é dado por:
1071,00
SR = ────────── x 100 = R$1.057,88
101,24
Esse procedimento é denominado deflaciona mento de salários e o
índice de preços usado na determinação do salário real é chamado deflator.
Processo semelhante pode ser empregado para deflacionar outras
séries temporais.
Assim, substituindo em (1) “salário” por “valor”, obtemos a fórmula (2):
(2)
St
SR = ────────── x 100
IPt
Vt
VR = ────────── x 100
IPt
236

Exemplo:
Tomando como exemplo o faturamento de uma empresa no período de
1991 a 1994, dado pela tabela abaixo, vamos determinar o seu faturamento
real, relativamente:
a. ao período de 1990;
b. ao período de 1991.
Anos Faturamento
(R$)
IP
1990 = 100
1991
1992
1993
1994
180.000
220.000
430.000
480.000
140,8
291,1
362,5
410,3
a. Para obtermos o faturamento da empresa relativamente ao ano de
1990, basta dividirmos cada valor constante da coluna referente ao faturamento
pelo índice geral de preços do respectivo ano. Com isso, estamos
deflacionando a série. Assim:
180.000 x100 = 127.841 430.000 x 100 = 118.620
140,8 362,5
220.000 x 100 = 75.575 480.000 x 100 = 116.988
291,1 410,3
237

Logo:
Anos Faturamento a Preços de 1990
(R$)
1991
1992
1993
1994
127.841
75.575
118.620
116.988
b. A fim de obtermos o faturamento da empresa, em termos de preços
de 1991, devemos, inicialmente, mudar a base do ano 1990 para o de 1991 e,
em seguida com em a. Assim:
IP91,92 = 291,1 x 100 = 206,7
140,8
IP91,93 = 362,5 x 100 = 257,5
140,8
IP91,94 = 410,3 x 100 = 291,4
140,8
Donde:
220.00 x 100 = 106.434
206,7
430.000 x 100 = 166.990
257,5
480.000 x 100 = 164.722
291,4
238

Logo:
Anos Faturamento
(R$)
IP
1991= 100
Faturamento a Preços de 1991
(R$)
1991
1992
1993
1994
180.000
220.000
430.000
480.000
100,0
206,7
257,5
291,4
180.000
106.434
166.990
164.722
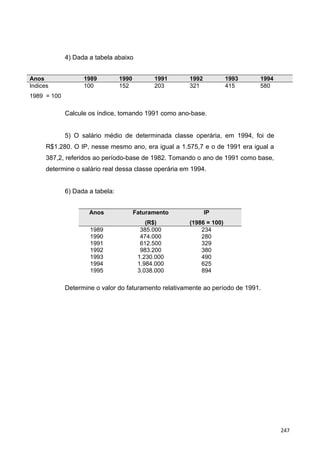
Pelo exame da tabela, vemos que o faturamento, no ano de 1994, foi,
em termos reais, inferior ao de 1991, embora, em termos nominais, tenha
aumentado.
Exemplo 2:
Uma categoria funcional está em negociação salarial com o empregador.
O salário atual da categoria é de R$2800,00. O empregador fez uma proposta
de reajuste salarial de 12,5% à categoria. O índice de preço do período é de
90%. A categoria deve aceitar a proposta do empregador?
Solução:
Salário Nominal com o aumento(SNA):
SNA= [2800 x 0,125] + 2800 = 350 + 2800 = R$ 3150,00
239

Salário Real com o aumento(SRA):
3150,00
SRA = ─────────── x 100 = R$ 3500,00
90
Conclusão:
Portanto, o salário real da categoria se elevaria para R$ 3500,00 e a
categoria teria um aumento real de seu poder aquisitivo, sendo a proposta
vantajosa, que deve ser aceita.
240

Taxa Média de Crescimento Anual
Outra técnica estatística para análise do crescimento de
fenômenos demográficos, financeiros e econômicos ao longo de uma
série temporal é a taxa média de crescimento anual.
A taxa média anual é um número relativo à população inicial e final
do período e o lapso de tempo decorrido no período. Utilizaremos os
símbolos P0, P1, ∆P0, n, r, sendo:
P0 = população inicial do período em estudo
P1 = população final do período em estudo
∆P0 = aumento registrado no período ou diferença de P1 – P0
n = número de anos decorridos
r = taxa media anual de crescimento( por 100 ou 1.000)
Aplicando estes símbolos temos que a fórmula de taxa média
aritmética de crescimento anual é a seguinte, em termos percentuais(por
100):
100 ∆P0
P0
r = ————————
n
Esta fórmula é aplicável quando o número de anos decorridos no
período (n) é pequeno, porque a população não cresce em progressão
aritmética quando n é grande.
241

Exemplo 1:
A série temporal a baixo apresenta a evolução do total de turistas na
cidade X no período de 2001 a 2010. A referida série, apresentada
abaixo, indica na última coluna o cálculo dos números-índices tendo como
ano-base 2001.
Evolução da Taxa Básica de Juros no País X no Período de 2001 a 2010.
Anos Turistas Número-Índice(NI)
2001 1,50 100
2002 1,65 110
2003 1,80 120
2004 1,95 130
2005 2,10 140
2006 2,25 150
2007 2,40 160
2008 2,55 170
2009 2,70 180
2010 2,85 190
Vamos calcular a taxa de crescimento anual da evolução da taxa
de juros no país X, no período de 2001 a 2010, constante da tabela
acima.
Solução:
P0 = 1,50
P1 = 2,85
∆P0 = 2,85 – 1,50 = 1,35
n = 2010 – 2001 = 9 anos
242

Logo,
100 x ( 1,35/1,50)
r= ———————— = (90/9) = 10%
9
Portanto, a taxa média aritmética de crescimento anual da básica
de juros no país X foi de 10%.
A taxa média de crescimento anual é de grande utilidade em
administração e economia, uma vez que possibilita fazer estimativas para
anos intermediários de cujos dados não dispomos(interpolação) ou
estimativas para anos futuros(extrapolação).
Exemplo:
Assim, se não dispuséssemos dos dados de 2003 da tabela do
exemplo 1, poderíamos obter sua estimativa por interpolação, utilizando a
taxa média que calculamos tendo encontrado 10%. Para o cálculo
teremos a seguinte fórmula derivada da anterior:
Px = P0 [1 + (r.n/ 100)]
Onde:
Px = população procurada
P0 = população inicial do período
r = taxa média de crescimento
n = lapso de tempo entre o ano inicial(P0) e o ano procurado(Px)
243

Portanto, sendo:
Px = população procurada
P0 = 1,50
r = 10%
n = 2003 – 2001 = 2
Logo:
Px = 1,50[ 1 + (10. 2/100)] = 1,80, exatamente o valor observado para este
dado em 2003 na tabela do exemplo 1.
Logo, a estimativa da taxa de juros básica no país X para 2003 é
de 1,80 %, segundo a taxa média de crescimento anual.
244

1) Resolva os problemas abaixo:
a) Em 1999, uma loja vendeu 1000 unidades de sandálias ao preço
unitário de R$ 25,00. Em 2000, vendeu 1200 unidades do mesmo
produto ao preço unitário de R$ 30,00. Determine os índices
relativos de preço, quantidade e valor simples das sandálias com
base em 1999.
b) O preço do pãozinho francês, em 1999, foi de R$ 0,12. Em 2000
passou para R$ 0,15. Qual foi a variação média de preço neste
período?
c) Uma papelaria vendeu, em 1998, 400 unidades de canetas Faber
Fix. Já em 1999, vendeu 300 unidades. Calcule o relativo de
quantidade e interprete o resultado, tomando 1998 como ano
base.
d) Em 1994, um supermercado vendeu 11,5 kg de café à R$ 5,00 o
quilo. Em 2000, vendeu 12,00 kg do mesmo produto ao preço de
5,20 o quilo. Qual o percentual do valor de aumento das vendas
neste período? (1994 = 100)
e) Uma pesquisa revelou, em janeiro de 2000, que um candidato a
prefeito de um cidade teria 50% dos votos válidos nas eleições de
outubro de 2000. Em maio do mesmo ano as intenções de voto
caíram para 35% do mesmo candidato. Qual foi a variação da
preferência pelo candidato neste período, tomando janeiro de
2000 como período base.
245

2) Pesquise na Internet, no site www.insvetigshopping.com.br os
principais índices do mercado financeiro e o que medem cada um deles.
3) A tabela abaixo se refere aos preços médios e consumo mensal de
uma amostra selecionada de materiais de escritório em um
departamento, de 1970 a 1975:
Item Unidade Preço Médio Consumo Mensal
1970 1975 1970 1975
Papel A4 Resma 0,70 1,48 4,5 8,0
Almofadas Cada 0,30 0,35 10,0 16,0
Esferográficas Cada 0,39 0,39 8,0 12,0
Lápis Dúzia 0,48 0,48 1,0 1,5
Clips Caixa 0,10 0,20 2,0 3,0
Pede-se:
a) O Índice de Laspeyres de Preço de 1975, tomando 1970 como ano
base;
b) O Índice de Laspeyres de Quantidade de 1975, tomando 1970 como
ano base;
c) O Índice de Paasche de Preço de 1975, tomando 1970 como ano
base;
d) O Índice de Paasche de Quantidade de 1975, tomando 1970 como
ano base;
e) O Índice de Fischer de Preço de 1975, tomando 1970 como ano base;
f) O Índice de Fischer de Quantidade de 1975, tomando 1970 como ano
base.
246

4) Dada a tabela abaixo
Anos 1989 1990 1991 1992 1993 1994
Indices
1989 = 100
100 152 203 321 415 580
Calcule os índice, tomando 1991 como ano-base.
5) O salário médio de determinada classe operária, em 1994, foi de
R$1.280. O IP, nesse mesmo ano, era igual a 1.575,7 e o de 1991 era igual a
387,2, referidos ao período-base de 1982. Tomando o ano de 1991 como base,
determine o salário real dessa classe operária em 1994.
6) Dada a tabela:
Anos Faturamento
(R$)
IP
(1986 = 100)
1989 385.000 234
1990 474.000 280
1991 612.500 329
1992 983.200 380
1993 1.230.000 490
1994 1.984.000 625
1995 3.038.000 894
Determine o valor do faturamento relativamente ao período de 1991.
247

7) Se os preços dos cigarros aumentam 70% e , como consequencia , o
ICV sobe 1,8%, que ponderação tem esse bem econômico dentro do custo de
vida?
8) O IP, em dado período, aumenta de 15%. Qual deve ser o aumento
dos salário dos empregados de uma empresa, para que tenham um aumento
real de 5%?
9)Dada a tabela abaixo:
Anos Preços
2005 1128,0
2006 1165,2
2007 780,9
2008 859,3
a)Calcule os elos relativos;
b)Considerando 2005 como ano-base, calcule os relativos em cadeia.
248

10)O salário de um funcionário deve ser deflacionado pelo setor de
recursos humanos da empresa. O empregado percebeu em novembro de 2009
o valor líquido de 4502,25. O poder aquisitivo deve ser calculado com base no
deflator de novembro de 2009. Se os dados disponíveis são dados pela tabela
abaixo, qual o valor do salário deflacionado do colaborador da empresa?
Meses IPCA(IBGE)
Agosto 0,02
Setembro 0,04
Outubro 0,04
Novembro 0,05
Dezembro 0,07
11)Uma Pesquisa de Orçamento Familiar revelou a "cesta de consumo"
de itens que melhor representa os “gastos” de uma família que ganha de 1 a 5
salários mínimos. A referida cesta está apresentada na tabela abaixo:
Cesta de Consumo
Item
Luz
Água
Telefone
Gasolina
Alimentação
Na tabela seguinte são apresentadas as quantidades consumidas pela
família, o valor unitário dos itens da cesta de consumo no primeiro dia do mês e
no último dia do mês de referência pela família investigada.
Unitário(R$)
do Consumo
Valor
Unitário(R$)
do Consumo
249

da Cesta no 1º
dia do Mes
da Cesta no
31º dia do Mes
Luz 100 kWh 0,30 0,34
Água 20 m3
0,50 0,60
Total ── ── ──
Calcule o índice de inflação do mês, considerando esta família uma
amostra representativa das famílias do país.
250

12)Correlacione os índices de preços agregativos produzidos no Brasil com
suas respectivas característica e metodologias.
1 Índice Nacional de Preços ao Consumidor- INPC
2 Índice Preços ao Consumidor Amplo- IPCA
3 Índice Nacional de Preços ao Consumidor Amplo Especial– IPCA-E
4 Índice Preços ao Consumidor Amplo 15- IPCA-15
5 Índice Geral de Preços- IGP
6 Índice Geral de Preços 10- IGP-10
7 Índice Geral de Preços- Disponibilidade Interna- IGP-DI
8 Índice Geral de Preços do Mercado- IGP-M
9 Índice de Preços ao Consumidor da FIPE- IPC-FIPE
10 Índice de Preços ao Consumidor Semanal-IPC-S
11 Índice de Preços ao Consumidor Semana l-São Paulo- IPC-SP
251

É medido pela FGV. Registra a inflação de preços desde matérias-primas agrícolas e industriais até
bens e serviços finais. A pesquisa de preços é feita entre o dia 21 do mês anterior até o dia 20 do mês
atual. Abrange toda a população, sem restrição de nível de renda.
É medido pela FGV. Calcula a variação de preços de produtos e serviços em sete capitais do país.
Registra a evolução de preços de maneira quadrissemanal. Calculado através de uma Pesquisa de
Orçamento Familiar, a POF, e indica o custo de vida de famílias de 1 a 33 salários mínimos
residenciais nas grandes regiões metropolitanas do país.
É medido pelo IBGE. É considerado o índice oficial da inflação do país. Oferece a variação dos preços
no comércio para o público final. Reflete o custo de vida de famílias com renda mensal de 1 a 44
salários mínimos.
bens e serviços finais. Faz medições no mês cheio, de 1 a 30 ou 31 de cada mês. Abrange toda a
população, sem restrição de nível de renda.
É medido pelo IBGE. Oferece a variação dos preços no mercado varejista. Reflete o custo de vida de
famílias com renda de 1 a 44 salários mínimos. É divulgado ao final de cada trimestre. Seu objetivo é
realizar um balanço trimestral da inflação.
bens e serviços finais. Mede a evolução de preços no período compreendido entre o dia 11 do mês
anterior e o dia 10 do mês atual. È usado em reajustes de tarifas públicas, contratos de aluguel e
planos de saúde. Abrange toda a população, sem restrição de nível de renda.
É medido pela FIPE. Mede a inflação na cidade de São Paulo. È calculado medindo-se o mês cheio,
de 1 a 30 ou 31 e de maneira quadrissemanal. O indicador reflete o custo de vida de famílias com
renda mensal de 1 a 20 salários mínimos. É utilizado como indexador informal para contratos da
prefeitura de São Paulo.
É medido pelo IBGE. Oferece a variação dos preços no mercado varejista. Reflete o custo de vida de
famílias com renda de 1 a 44 salários mínimos. É calculado a cada 15 dias e mostra uma comparação
mais precisa da alta e queda dos preços. É utilizada para reajuste do IPTU.
É medido pelo IBGE. Calculado a partir dos índices de preços ao consumidor regionais. Oferece a
variação dos preços no mercado varejista. Atinge famílias até 6 salários mínimos.
É medido pela FGV. Calcula a variação de preços de produtos e serviços na cidade de São Paulo.
Registra a evolução de preços de maneira quadrissemanal. Calculado através de uma Pesquisa de
Orçamento Familiar, a POF, e indica o custo de vida de famílias de 1 a 33 salários mínimos
residenciais na cidade de São Paulo. É usado para cálculo do IGP. Serve de referência para reajustes
salariais e contratos de aluguéis.
bens e serviços finais. È formado pela média de três índices: IPA, IPC e INCC. È usado em reajustes
de tarifas públicas, contratos de aluguel e planos de saúde. Abrange toda a população, sem restrição
de nível de renda.
252

13)A série temporal abaixo apresenta a evolução da população de clientes
inadimplentes com Cheque Especial do Banco A do Rio de Janeiro no período
de 2001 a 2006. Calcule os relativos em cadeia com base no ano de 2001 e os
elos relativos.
Evolução da População de Clientes Inadimplentes com Cheque Especial
do Banco A do Rio de Janeiro no período de 2001 a 2006.
Anos Clientes
Inadimplentes
(Em Mil)
Relativos em
cadeia(2001=100)
Elos relativos
2001 20
2002 24
2003 30
2004 32
2005 34
2006 38
14)Vamos calcular a taxa de crescimento anual da evolução da população de
clientes inadimplentes com Cheque Especial do Banco A do Rio de Janeiro no
período de 2001 a 2006 do exercício anterior.
15)Assim, se não dispuséssemos dos dados de 2004 do exercício 5, qual a
estimativa da população de clientes inadimplentes com Cheque Especial do
Banco A para 2004?
253

Unidade X
Análise Exploratória de Dados
Introdução:
A idéia da análise exploratória de dados é confrontar, passo a passo,
de forma mais complementar de que antológica, os métodos clássicos da
estatística descritiva e os métodos modernos de análise exploratória de dados.
A ponte de transição é a ênfase dada aos procedimentos ou métodos
resistentes. Na análise de coleção de dados não é raro aparecerem
observações anormais ou extravagantes em completo contraste com o
comportamento da maioria. A presença de tais observações discrepantes
levanta problemas complexos: por um lado, podem ser compatíveis com a
natureza do próprio fenômeno que as gerou e convém que sejam retidas; por
outro lado, podem ser fruto de erros humanos cometidos na coleta ou registro
dos dados e convém que sejam eliminadas ou corregidas. Trata-se de um
difícil caso de identificação que acaba por revelar-se dilemático. O que é de
fato importante ou é extremo, pouco usual? É esse o príncipio básico da
análise exploratória de dados. Contudo, os procedimentos ditos resistentes
não são afetados pela presença de dados discrepantes(outliers), mas chamam
atenção para a sua presença e para a necessidade de uma análise
individualizada e pormenorizada. Nos ocuparemos neste capítulo dos métodos
resistentes.
A estatística descritiva(tabelas, gráficos e medidas descritivas) pode-se
dizer que tem cobertura em praticamente todos os softwares de
estatística(Excel, SPSS, Statistica, SAS, R, etc). A análise exploratória de
dados, por ser relativamente recente e de aplicação menos generalizada, tem
menor cobertura. O SPSS é um dos poucos pacotes que que se ocupa mais
extensamente de tal análise.
254

Nas aplicações às ciências sociais e humanas, a precisão conseguida
pela utilização do método estatístico fica severamente dependente da
qualidade das medidas e das observações, podendo eventualmente a ordem
de grandezas dos erros ser irrelevante para a qualidade do resultado
estatístico. Para tanto, é que se justifica a pesquisa que modernamente se faz
de métodos resistentes, que sejam insensíveis à presença de erros grosseiros
ou valores anormais(outliers) ou de um grande número de pequenos erros
(arredondamentos, etc).
O presente capítulo tem o objetivo de fazer uma introdução à análise
exploratória de dados, sem grandes preocupações sobre a distinção entre
estatística descritiva e análise exploratória de dados(AED), em relação a qual
parece não haver consenso entre os pesquisadores. Para uns, a AED é uma
parte da estatística descritiva, mas para outros, explorar não é a mesma coisa
que descrever.
Os principais objetivos, contudo, da análise de dados é:
1. Exploração dos dados para descobrir ou identificar os aspectos ou
padrões de maior interesse, assimetrias e dados discrepantes;
2. Descrição através de resumo e representação dos dados de maneira
a destacar ou chamar a atenção para os aspectos mais gerais do
comportamento dos dados.
As técnicas que tratam o ponto (1) correspondem à AED e as que tratam
do ponto(2) correspondm à estatística descritiva. Contudo, ambas recorrem
largamente ao emprego de métodos numéricos e gráficos.
A AED teve origem há cerca de 20 anos com os trabalhos de John W.
Tukey realizados na Universidade de Princeton e nos Laboratórios Bell. Esse
trabalhos culminaram com a publicação das duas obras pioneiras: Exploratory
Data Analysis(Tukey,1977) e Data Analysis and Regression(Tukey e Mosteller,
1977). Para Tukeya a AED é trabalho de detetive: “trabalho de detetive com
números, trabalho de detetive com contagens, trabalho de detetive com
255

gráficos”.
A incerteza põe limitações à AED e às respectivas conclusões, na
medida em que o mesmo fenômeno pode dar lugar a diferentes observações
ou que a mesma população pode dar lugar a diferentes amostras. Assim, para
avaliar a estabilidade das medidas descritivas é necessário conhecer de algum
modo o que se passa com a família de amostras alternativas(que podiam ter
sido obtidas mas que não foram) de modo a tentar determinar, para cada
medida descritiva, um erro de amostragem. O erro de amostragem é uma das
manifestações da chamada incerteza interna das observações que compõem
a amostra. A incerteza subsidiária, erro não amostral, que pode ter várias
causas(erros sistemáticos de medida, cobertura incompleta da área, fraudes
em entrevistas, coleta e inserção incorreta de dados, etc), não se manisfesta
nos dados comumente. Um bom plano de amostragem ou uma experiência
bem delineada pode permitir controlar a incerteza interna e reduzir a incerteza
subsidiária.
Depois da AED identificar características e padrões de uma amostra de
dados, caso se pretendam ladear as limitações decorrentes da incerteza, há
que recorrer à Análise Confirmaória de Dados(ACD). A ACD avalia a
possibilidade de reprodução dos padrões ou estimativas verificadas no estudo
descritivo e exploratório. O seu papel é semelhante ao da inferência estatística
clássica, na medida que possibilita asserções sobre a significância e confiança,
embora integrando frequentemente tais passos:
1. Incoporar informação decorrente da análise de dados adicionais,
diferentes mas relacionados com a coleção em estudo;
2. Validar resultados recolhendo e analisando novas coleções.
Em resumo, se a AED é trabalho de detetive, que procura pistas e
evidências, a ACD é trabalho judicial ou quase judicial, que analisa e avalia a
força das provas e da evidência. Infelizmente, inferência e análise confirmatória
de dados saem do escopo do presente livro.
256

Passaremos, agora doravante, a apresentar algumas técnicas básicas
de AED. Existem um gama bastante variada e diversificada destas técnicas,
mas estudaremos as mais básicas e usuais.
Conceito
A análise exploratória de dados (AED) é um conjunto essencial e
indispensável de ferramentas que nos permite organizar, sumariar e interpretar
dados rapidamente e sem procedimentos estatísticos complicados. A AED
deve ser sempre o primeiro passo do processo de análise, porque ao analisar
os dados podemos constatar quais os traços ou padrões mais evidentes.
Denomina-se Análise Exploratória de Dados (AED) a uma coleção de
técnicas e estratégias para analisar bancos de dados estatísticos com a
intenção de estudar padrões e relações entre variáveis. Essas informações são
importantes para subsidiar posterior modelagem estatística com fins de
generalização. Além de apresentar os recursos clássicos de Estatística
Descritiva, a disciplina de AED tem forte ênfase na construção de
representações gráficas de dados. Para fazer isso com eficiência o estudante
deverá aprender simultaneamente a utilizar o software SPSS, dentre outros,
como ferramenta computacional.
Importância da AED:
A importância AED se resume nos seguintes pontos:
o Quando se conduz uma investigação há naturalmente várias
expectativas ou hipóteses em relação aos resultados. Através da AED
rapidamente ficam com uma ideia de como essas expectativas se
confirmam ou não;
o Por outro lado, a AED permite ao investigador ver padrões nos dados
que não estavam debaixo de hipóteses e que podem ser interessantes
257

na interpretação dos resultados da pesquisa. E isto não é feeling, é
encontrar algo que os “olhos” do investigador não conseguiam ver
apriori, porque, por exemplo, o fenómeno em estudo não era
suficientemente conhecido pela sociedade científica;
o Outra vantagem óbvia é a ajuda na detecção de erros relacionados com
a entrada dos dados (não devia acontecer, mas acontece aos
melhores!). Um determinado valor de um sujeito, suponhamos 1,78
metros de altura, que entrou como 178 afeta certamente as estatísticas
do grupo em estudo e a sua análise;
o Um outro aspecto importante é que algumas estatísticas podem ser
enganosas. Os testes são enganosos quando são mal aplicados, mal
usados e incorretamente interpretados. Determinados testes estatísticos
requerem dados com requisitos e pressupostos específicos. Se os
dados são apropriados para um teste estatístico específico poderão
fornecer informação mais útil; se não são apropriados poderão fornecer
dados sem significado.
o Infelizmente muitos investigadores partem cedo de mais para análise
estatísticas complexas sem explorar cuidadosamente os seus dados.
o Lembremo-nos do velho ditado acerca dos computadores: “Entra lixo,
sai lixo”. Isto significa que os resultados saídos do computador não são
melhores do que a informação que lá introduzimos. Com as estatísticas
passa-se o mesmo. Um teste estatístico não é mais do que um conjunto
de operações matemáticas. Se os números não são significativos ou se
um teste particular não é o apropriado, os resultados do procedimento
estatístico não terão significado. As estatísticas não gracejam, mentem,
ou decepcionam. As pessoas é que fazem dessas coisas. Para evitar
esses problemas, nós, os utilizadores das estatísticas, devemos
conhecer o mais possível os nossos dados. A AED permite, portanto,
chegar a esse intento.
258

1)Gráfico de Caule-e Folhas:
É um tipo de representação que se pode considerar entre a tabela e o
gráfico, uma vez que são apresentados os verdadeiros valores da amostra,
mas numa apresentação sugestiva, que faz lembrar um histograma.
Consiste em escrever do lado esquerdo de uma linha vertical o dígito (ou
dígitos) da classe de maior grandeza, seguidos dos restantes. A representação
obtida terá o seguinte aspecto:
Quando os dados não são numerosos, n pequerno, a análise e
descrição facilita-se com métodos semi-gráficos usando o gráfico de caule-e-
folhas .
A construção , apesar de imediata, permite que o observador, sem perda
de informação, se torne mais sensível ao aspecto geral dos dados. Além disso
o gráfico de caule-e-folhas é uma técnica flexível e eficiente para iniciar o
estudo de uma amostra, deixando aos dados coletados fazer a maior parte do
trabalho.
O gráfico de caule-e-folhas pode ser obtido diretamente sem maiores
complicações do software SPSS.
259

Exemplo 1:
Informação de salário de 36 funcionários sorteados ao acaso da
empresa MB.
4,00 6,86 8,74 10,53 13,23 16,22
4,56 7,39 8,95 10,76 13,60 16,61
5,25 7,59 9,13 11,06 13,85 17,26
5,73 7,44 9,35 11,59 14,69 18,75
6,26 8,12 9,77 12,00 14,71 19,40
6,66 8,46 9,80 12,79 15,99 23,30
Gráfico de Caule-e Folhas:
Fi CAULE FOLHA
2 4 0 5
2 5 2 7
3 6 2 7 9
3 7 4 4 5
3 8 0 5 6
5 9 0 0 4 8 8
2 10 5 8
2 11 0 5
2 12 0 8
3 13 1 5 9
2 14 6 6
0 15
3 16 0 1 6
1 17 3
1 18 8
1 19 3
0 20
0 21
0 22
1 23 3
260

Interpretação:
o Valores concentrados entre 4 e 19;
o Leve assimetria na direção dos valores grandes( assimétrica à direita);
o Destaque do valor 23.3.
Exemplo 2:
Os dados abaixo representam as notas de satisfação de 0 a 10
dadas por 20 clientes ao atendimento por telefone de uma rede de
telefonia celular:
1.5
8.5
6.5
8.5
7.5
8.5
7.0
8.5
8.0
10.0
7.0
9.5
8.5
2.5
8.5
8.5
8.5
7.5
9.0
8.5
261

Gráfico de Caule-e-Folhas
A fugura está diferente
Frequências Caule Folhas
1
1
1
2
5
5
1 6 5
4 7 0055
10 8 0555555555
2 9 05
1 10 0
Cada caule é a parte inteira e as casas decimais as folhas.
Então o caule 2 tem uma folha e o caule 7 tem 4 folhas. O gráfico
acima permite verificar alguns padrões: o grau de satifação
predominate está entrre 7 e 8,5 e existem duas observações extremas
1,5 e 2,5. A distribuição é mais longa à esquerda, em direção aos
valores mais baixos, portanto com assimetria negativa.
262

2)Gráfico de Extremos-e-Quartis ou Caixa-com-Bigodes:
É um tipo de representação gráfica, em que se realçam algumas
características da amostra. O conjunto dos valores da amostra
compreendidos entre o 1º e o 3º quartis, que vamos representar por
Q1 e Q3 é representado por um retângulo (caixa) com a mediana
indicada por uma barra. A largura do retângulo não dá qualquer
informação, pelo que pode ser qualquer. Consideram-se seguidamente
duas linhas que unem os meios dos lados do retângulo com os
extremos da amostra. Para obter esta representação, começa por se
recolher da amostra, informação sobre 5 números, que são: os 2
extremos (mínimo e máximo), a mediana e o 1º e 3º quartis. A
representação do diagrama de extremos e quartis tem o seguinte
aspecto:
O extremo inferior é o mínimo da amostra(Xmim), enquanto que o
extremo superior é o máximo da amostra(Xmax).
263

O gráfico,então, baseia-se na localização dos quartis( 1º quartil,
2º quartil ou mediana e 3º quartil), que definem assim 4 sub-intervalos,
cada um 25% das observações:
1º intervalo quartílico : Xmin e Q1
2º intervalo quartílico : Q1 a Q2
3º intervalo quartílico : Q2 a Q3
3º intervalo quartílico : Q3 a Xmax
São considerados outliers as observações que fiquem abaixo do
limite definido pela expressão Q1-1,5(Q3-Q1) ou acima do limite
Q3+1,5(Q3-Q1). Visualmente isso significa observações acima e/ou
abaixo dos bigodes.
O gráfico de extremos-e-quartis ou caixa-com-bigodes é uma útil
representação dos dados na detecção de outliers ou dados
discrepantes e na análise da simetria e de sub-intervalos de
concentração da amostra de valores.
264

Exemplo 1:
Do exemplo 1, temos o seguinte gráfico de Extremos-e-
Quartis:
36N =
SALÁRIOS
30
20
10
0
Curva mais longa em valores mais altos e o valor 23,3 apesar
de ser destaque não é um outlier.
265

Exemplo 2:
Do exemplo anterior, temos o seguinte gráfico de Extremos-e-
Quartis:
Gráfico correto:
20N =
NOTAS
12
10
8
6
4
2
0
14
1
Observando o gráfico acima notamos que existem duas
observações discrepantes: a da 1ª posição: 1,5 e da 14ª posição: 2,5.
A área em cinza é o intervalo que vai de Q1 a Q3, onde se concentram
a maioria dos valores da série: entre 7 e 8,5. Com estes dois valores
extremos a curva se alonga para a esquerda.
266

3)Gráfico de Probabilidades(P-P):
Os gráficos de probabilidades visualizam graficamente o ajuste
de uma variável a uma curva teórica de freqüência, que também pode
ser chamada de distribuição de probabilidades. O mais usual é utilizá-
lo, assim como o histograma, para avaliar o ajuste de uma curva de
freqüência à Curva Normal. A diagonal do gráfico representa um
ajustamento perfeito da amostra à Curva Normal.
Quanto mais os pontos se afastam da diagonal,
menor é o ajustamento da amostra à distribuição normal.
Exemplo:
Do exemplo anterior, temos o seguinte gráfico de P-P:
Gráfico P-P das Notas
Frequências Relativas Observadas
1.00.75.50.250.00
FrequênciasRelativasEsperadas
1.00
.75
.50
.25
0.00
Observando o gráfico P-P das notas constatamos o mau ajustes
das notas ao modelo normal, pois a maioria das notas estão afastadas
da diagonal.
267

4)Gráfico do Ajustamento dos Resíduos:
Se a amostra é perfeitamente normal, os pontos existentes no
gráfico distribuir-se-ão segundo uma faixa horizontal em torno de zero,
sem denotar qualquer padrão de distribuição.
Do exemplo anterior, temos o seguinte gráfico de Ajustamento
dos Resíduos:
Gráfico do Ajustamento dos Resíduos
Frequências Relativas Acumuladas
1.0.8.6.4.20.0
DesviodaNormal
.2
.1
0.0
-.1
-.2
Percebe-se que os pontos do gráfico apresentam alguns
padrões de tendência, formando pequenos grupos, o que ratifica a não
normalidade das notas de satisfação com a telefonia.
As distribuições de frequências com o seu histograma, o polígno
de frequência e parâmetros característicos podem também, somadas
às técnicas que acabamos de estudar, ser usadas na análise
exploratória de dados colhidos de uma amostra.
268

1)Construir e interpretar o histograma da amostra abaixo de 30 tempos
de espera de embarques de turistas em um aeroporto:
5 10 15 15 20 20 25 25 25 25 30 30 30 30 30
30 30 30 30 30 35 35 40 45 45 50 50 55 60 60
2)Costruir um gráfico de Caule-e-Folhas para as alturas de 40 atletas
estrangeiros no país e interpretar os resultados
1,50 1,51 1,51 1,55 1,60 1,60 1,61 1,61 1,61 1,65 1,65 1,65 1,65 1,65 1,70
1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,72 1,72 1,72 1,72 1,75 1,75
1,75 1,80 1,80 1,81 ,181 1,83 1,83 1,83 1,90 1,90
3)Costruir um gráfico Caixa-com-Bigodes para as alturas de 40 atletas
estrangeiros no país e interpretar os resultados:
1,50 1,51 1,51 1,55 1,60 1,60 1,61 1,61 1,61 1,65 1,65 1,65 1,65 1,65 1,70
1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,72 1,72 1,72 1,72 1,75 1,75
1,75 1,80 1,80 1,81 ,181 1,83 1,83 1,83 1,90 1,90
269

4)Costruir um gráfico de Probabilidade para as alturas de 40 atletas
estrangeiros no país e interpretar os resultados:
1,50 1,51 1,51 1,55 1,60 1,60 1,61 1,61 1,61 1,65 1,65 1,65 1,65 1,65 1,70
1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,70 1,72 1,72 1,72 1,72 1,75 1,75
1,75 1,80 1,80 1,81 ,181 1,83 1,83 1,83 1,90 1,90
5)Costruir um gráfico de Caixa-com-Bigodes para as populações dos
30 maiores municípios do Brasil, segundo o censo de 1980, dadas na
tabela abaixo(em 10.000 habitantes) e interpretar os resultados:
Municípios População
São Paulo 849,3
Rio de Janeiro 509,3
Belo Horizonte 178,1
Salvador 150,6
Fortaleza 130,8
Recife 120,4
Brasília 117,7
Porto Alegre 112,5
Nova Iguaçu 109,4
Curitiba 102,5
Belém 93,4
Goiânia 71,7
Campinas 66,4
Manaus 63,4
São Gonçalo 61,4
Duque de Caxias 57,5
Santo André 55,2
Guarulhos 53,2
Osasco 47,3
São Luís 44,9
São Bernardo do Campo 42,5
Natal 41,7
Santos 41,6
Niterói 40,1
270

Municípios População
Maceió 40,0
São João de Meriti 39,8
Teresina 37,8
Campos 34,9
Jaboatão 33,1
João Pessoa 33,0
6)Abaixo estão apresentados os 30 programas de maior audiência em
2011 no Brasil, segundo o IBOPE- Praça PNT- Índice de Audiência
Domiciliar( % ), média de janeiro a maio de 2011:
Programas da TV Globo Audiência Domiciliar
Novela II 35.7
Jornal Nacional 31.9
Novela II 30.5
Praça TV 2a Edição 28.5
Big Brother Brasil 27.0
Novela II 26.2
Festival Nacional 26.2
A Grande Família 26.2
Show de Terça 1 25.9
Futebol/Futebol Reg-quarta-feira 23.1
Tela Quente 22.6
Fantástico 22.0
Globo Repóter 21.6
Malhação 21.2
Zorra Total 21.2
Futebol Matutino 19.4
Vale a pena Ver de Novo 19.4
Futebol/Futebol Reg Vespertino 19.4
Carnaval Vespertino 19.0
Show de Terça - Feira 17.6
Chico e Amigos 17.5
Domigão do Faustão 17.2
Temperatura Máxima 16.8
Série Brasileira 16.4
Cinema Nacional 16.1
Os Caras de Pau 15.6
Sessão da Tarde 15.4
Central da Copa Vespertino 15.1
Caldeirão do Huck 15.1
Acampamento de Férias 15.0
Realize uma AED através do histograma, polígono de frequência,
Caule-e Folhas e Caixa-com-Bigodes.
271

7)Pesquise um conjunto de 30 valores de pesos de pessoas e faça
uma análise exploratória dos dados construindo os gráficos:
a)Caule-e-Folhas;
b)Caixa-com-Bigodes;
c)Gráfico de Probabilidades;
d)Gráfico de Ajustamento dos Resíduos.
272

Texto 1
Arredondamento de Dados
Introdução:
Como sabemos, os números resultam de uma mensuração no seu sentido
mais amplo, a qual só pode ser exata quando assume a forma de contagem
ou enumeração, em números naturais, de coisas ou unidades mínimas
indivisíveis. Em tais casos a variável pode assumir valores discretos. Outras
mensurações se dão numa escala contínua, que pode teoricamente, ser
indefinidamente subdividida. Na prática, porém, há sempre um limite para a
precisão com a qual a mensuração pode ser feita. O que nos leva a concluir
que o valor verdadeiro nunca é conhecido. Na verdade, os valores
observados são aproximados. Assim é que, se o comprimento de um
parafuso, medido em centímetros, foi dado por 4,6 cm, devemos considerar
que o valor exato desse comprimento será algum valor entre 4,55 cm e 4,65
cm, o que foi aproximado para 4,6 cm devido ao fato de a precisão adotada
na medida ser apenas de décimos de centímetros. Em nossos estudos,
faremos uso da seguinte convenção: a precisão da medida será
automaticamente indicada pelo número de casas decimais com que se
escrevem os valores da variável. Assim um valor 4,60 indica que a variável
em questão foi medida com precisão de centésimos, não sendo exatamente
o mesmo que 4,6 valor correspondente a uma precisão de décimos.
Arredondamento de Dados:
É a supressão de unidades inferiores às de determinada ordem.
274

Técnica de Arredondamento:
De acordo com a resolução 886/66 do IBGE, o arredondamento é feito da
seguinte maneira:
• Quando o primeiro algarismo a ser abandonado é 0, 1, 2, 3, ou 4, fica
inalterado o último algarismo a permanecer.
Ex: 53,24 passa a 53,2
• Quando o primeiro algarismo a ser abandonado é 6, 7, 8, ou 9, aumenta-se
de uma unidade o último algarismo a permanecer.
Ex: 42,87 passa a 42,9
25,08 passa a 25,1
53,99 passa a 54,0
•Quando o primeiro algarismo a ser abandonado é 5, há duas soluções:
1) Se ao 5 seguir em qualquer casa, um número diferente de zero, aumenta-
se uma unidade ao algarismo a permanecer
Ex: 2, 352 passa a 2,4
25,6501 passa a 25,7
275

2)Se o 5 for o último algarismo ou ao 5 só se seguirem zeros, o último
algarismo a ser conservado só será aumentado de uma unidade se for
ímpar .
Ex : 24,75 passa a 24,8
24,65 passa a 24,6
24,75000 passa a 24,8
24,6500 passa a 24,6
Observação:
Não devemos nunca fazer arredondamentos sucessivos .
Ex :
17,3452 passa a 17,3 e não para 17,35 para 17,4
Se tivermos necessidade de um novo arredondamento fica recomendado
a volta aos dados originais.
276

Compensação:
Suponhamos os dados abaixo, aos quais aplicamos as regras de
arredondamento:
25,32 25,3
17,85 17,8
10,44 10,4
+31,17 +31,2
————— —————
84,78 (84,8?)
(84,7)
Verificamos que houve uma pequena discordância: a soma é exatamente
84,7 quando, pelo arredondamento, deveria ser 84,8. Entretanto, para a
apresentação dos resultados, é necessário que desapareça tal diferença, o
que é possível pela prática do que denominamos compensação,
conservando o mesmo número de casas decimais. Praticamente, usamos
“descarregar” a diferença nas maiores parcelas.
Assim, passaríamos a ter:
25,3
17,8
10,4
+31,3
————
84,8
277

Observação:
Vale ressaltar que se houver uma diferença maior que uma unidade, usa-se
descarregá-la por unidade nas maiores parcelas. Convém, ainda, observar
que, se a maior parcela é igual ao dobro de qualquer outra parcela ou maior
que esse dobro, “descarregamos” a diferença maior que uma unidade apenas
na maior parcela.
278

Texto 2
Normas de Representação Tabular
Estas normas têm como objetivo orientar a apresentação racional e
uniforme de dados estatísticos, em forma tabular, no sistema estatístico,
subordinado à orientação normativa e supervisão técnica do IBGE.
Toda tabela estatística deve ser aberta nas laterais, fechada em cima e em
baixo com traços mais fortes.
Uma tabela estatística compõe-se de elementos essenciais e elementos
complementares. Os elementos essenciais de uma tabela são o título, o corpo, o
cabeçalho e a coluna indicadora.
O título é a indicação que precede a tabela e que contém a designação do
fato observado, local e a época em que foi registrado.
O corpo é o conjunto de colunas e linhas e que contém, respectivamente,
em ordem vertical e horizontal, as informações sobre o fato observado.
A casa é o cruzamento de uma coluna com uma linha. As casas não deverão
ficar em branco, apresentando sempre um número ou sinal convencional.
279

Quadro 1
Sinais Convencionais Mais Utilizados em Tabelas
Sinais Descrição
─ dado inexistente
... dado ignorado
? dado impreciso
0 dado que ao se dividir por uma potência de 10 ,não atinge a unidade
A coluna indicadora é a parte da tabela que especifica o conteúdo das linhas.
Uma tabela pode ter mais de uma coluna indicadora.
Os elementos complementares de uma tabela estatística são a fonte, as
notas e as chamadas, e se situam de preferência no rodapé da tabela.
A fonte é a indicação da entidade responsável pelo fornecimento dos dados
ou pela sua elaboração.
As notas são informações de natureza geral, destinadas a conceituar ou
esclarecer o conteúdo das tabelas ou indicar a metodologia adotada no
levantamento ou elaboração dos dados.
As chamadas são informações de natureza específica sobre determinada
parte da tabela, destinadas a conceituar ou esclarecer dados. As chamadas são
indicadas no corpo da tabela em algarismos arábicos, entre parênteses, à esquerda
nas casas e à direita na coluna indicadora. A numeração das chamadas na tabela será
sucessiva, de cima para baixo, e da esquerda para direita. A distribuição das
chamadas no rodapé da tabela obedecerá à ordem de sua sucessão na tabela,
separando-se uma das outras por um ponto.
As chamadas de uma tabela que ocupam mais de uma página devem figurar
no rodapé da tabela na última página, de acordo com sua sucessão na mesma.
280

Exemplo de Tabela Estatística de Acordo com as Normas do IBGE:
Tabela 1
Distribuição de Funcionários da Empresa Y Segundo Cargo Ocupado
Rio de Janeiro
Março/2010
Cargo Quantidade
Alta Administração 15
Gerencial 20
Técnico Superior Júnior(1) 80
Técnico Superior Senior(2) 60
Técnico de Nível Médio 125
Operacional Efetivo(3) 200
Operacional Terceirizado(4) ──
Estagiários ...
Total 500
Fonte: RH da Empresa Y
Nota: O levantamento foi realizado depois das demissões realizadas para contenção de despesas em
janeiro/fevereiro de 2010.
(1)Constituem profissionais de nível superior com menos de 5 anos de empresa. (2)Constituem
profissionais de nível superior com 5 anos ou mais de empresa. (3)São profissionais de nível elementar que
desempenham funções de auxiliares de serviços gerais e que possuem contratos de trabalho com a
empresa. (4) São profissionais de nível elementar que desempenham funções de auxiliares de serviços
gerais e que não possuem contratos de trabalho com a empresa. Trabalham na empresa mas são
contratados de outras corporações.
Texto 3
281

Construção de Distribuições de Frequência com Intervalos
de Classes
Seja uma amostra colhida de estaturas em centímetros de crianças nascidas
numa maternidade:
44 42 46 58 52 56 50 49 51
60 40 48 52 58 50 51 53 56
40 45 47 44 50 57 60 58 48
50 39 41 48 47 45 54 57 55
59 59 51 53 54 49 55 52 43
48 46 36 42 48 44 49 51 53
51 50 59 43 49 55 48 49 52
50 51 54 55 54 43 37 46 50
44 53 56 57 47 38 40 41 56
53 56 52 54 51 42 53 54 50
282

1º ) Apuração dos dados:
Medidas( em centímetros ) Apuração
36 |
37 |
38 | |
39 | |
40 | | |
41 | |
42 | | |
43 | | | |
44 | | | |
45 | | |
46 | | |
47 | | | |
48 | | | | | |
49 | | | | | |
50 | | | | | | | |
51 | | | | | | |
52 | | | | | | |
53 | | | | | |
54 | | | | | |
55 | | | | |
56 | | | | |
57 | | |
58 | | |
59 | | |
60 | | |
283

2º )Obter a distribuição de frequência simples:
Medidas ( em centímetros ) Apuração
36 1
37 1
38 2
39 2
40 3
41 2
42 3
43 4
44 4
45 3
46 3
47 4
48 6
49 6
50 8
51 7
52 7
53 6
54 6
55 5
56 5
57 3
58 3
59 3
60 3
Total 100
284

3º ) Obter o número de classes e o intervalo de classes:
Para obter o número de classes e o intervalo de classes deveremos aplicar
as fórmulas abaixo:
K = 1 + 3,3 log N , onde :
K = número de classes sugerida, arredondado para inteiro.
N= frequência total
h = R K , onde:
R= amplitude total, isto é, diferença entre o maior e menor valor da distribuição.
Cálculos para o exemplo:
K= 1 + 3,3 log 100 ≈ 8 classes
h=(60-36)8 = 3
Observação: o valor de K é o número de classes previstas para a distribuição. No
momento da montagem da tabela, pode ocorrer de se obter uma classe a mais ou
uma classe a menos do que o calculado na fórmula de K.
285

4º )Obter a distribuição de frequência com intervalo de classes:
Medidas ( em centímetros ) Fi
36 | 39 4
39 | 42 7
42 | 45 11
45 | 48 10
48 | 51 20
51 | 54 20
54 | 57 16
57 | 60 9
60 | 63 3
Total 100
Bibliografia
286

1. BARBETTA, PEDRO ALBERTO; REIS, MARCELO MENEZES;
BORNIA, ANTONIO CEZAR. Estatística para Cursos de Engenharia e
Informática. São Paulo. Editora Atlas, 2004.
2. BARNETT, V. Sample Survey: Principies and Methods. 3nd Edition.
London: Arnold,1974.
3. BOLFARINE, H ; BUSSAB, W. O. Elementos de Amostragem. São Paulo: ABE-
ProjetoFisher,2005.
4. BOLFARINE, HELENO; SANDOVAL, MÔNICA CARNEIRO. Introdução à
Inferência Estatística. Rio de Janeiro. Coleção Matemática Aplicada,2000.
5. BUSSAB. W. O. ; MORETTIN, P. A. Estatística Básica. 5ed. São Paulo. Saraiva,
2003.
6. CONOVER, W J. (1998) Practical Nonparametric Statistics. 3. ed. New
York: John Wiley.
7. COSTA, Giovani G . O. Curso de Estatística Básica: Teoria e Prática.
São Paulo. Editora Atlas, 2011.
8. COSTA, Giovani G . O. Curso de Estatística Inferencial e
Probabilidades: Teoria e Prática. São Paulo. Editora Atlas, 2012.
9. COSTA, Giovani G . O. ; GIANNOTTI, Juliana D. G. Estatística Aplicada
ao Turismo. Volumes 1 e 2. 3 ed. Rio de Janeiro: Fundação CECIERJ,
2010.
10.COSTA NETO, PEDRO LUIZ DE OLIVEIRA. Estatística. Editora Edgard
Blücher Ltda. São Paulo, 2002.
11.CRESPO, ANTÔNIO ARNOT. Estatística Fácil. São Paulo. Editora
Saraiva, 2000.
12.DE GROOT, M.H. ; SCHERVISH, MJ. Probability and Staíistics. 3ed.,
NewYork:Addison-//weley, 2002.
13.DURBIN, J., and WATSON, G. S. "Testing for Serial Correlation in Least
Squares Regression, I." Biometrika 37, 409–428,1950.
14.DURBIN, J., and WATSON, G. S, G. S. "Testing for Serial Correlation in
Least Squares Regression, II." Biometrika 38, 159–179,1951.
15.FREUND, JOHN E.; SIMON, GARY A. Estatística Aplicada: economia,
287

administração e contabilidade.Tradução: Alfredo Alves de farias. 9ed. Porto Alegre:
Bookman,2000.
16.GAUSS, CARL FRIEDRICH. Theoria Motus Corporum Coelestium in
Sectionibus Conicis Solem Ambientium. Estados Unidos. Paperback,
2011.
17. HAIR, JOSEPH F.; ANDERSON, ROLPH E.; TATHAM, RONALD L.;
BLACK, WILLIAN C. Análise Multivariada de Dados. Tradução: AdonaiSchlup
SabtáAnna e Anselmo Chaves Neto. Porto Alegre:Bookman., 5ed. 2005.
18.HOFFMANN, Rodolfo. (2006) Análise de Regressão. 4. ed. São Paulo:
Hucitec.
19.JARQUE, CARLOS M.; BERA, ANIL K. "Efficient tests for normality,
homoscedasticity and serial independence of regression residuals".
Economics Letters 6 (3): 255–259. doi:10.1016/0165-1765(80)90024-
5,1980
20.JARQUE, CARLOS M.; BERA, ANIL K. "Efficient tests for normality,
homoscedasticity and serial independence of regression residuals:
Monte Carlo evidence". Economics Letters 7 (4): 313–318.
doi:10.1016/0165-1765(81)90035-5, 1981
21.JARQUE, CARLOS M.; BERA, ANIL K. "A test for normality of
observations and regression residuals". International Statistical Review
55 (2): 163–172. JSTOR 1403192, 1987.
22. JUDGE; et al. Introduction and the theory and practice of econometrics
(3rd ed.). pp. 890–892, 1982.
23.JOHNSON, Richard; WICHERN, Dean. Applied Multivariate Statistical
Analysis. 6. ed. New Jersey: Prentice Hall, 2007.
24.JÚNIO, Joseph F. Hair ; BALIM, Barry; MONEY Artur H.; SAMOUEL,
Phillip. Fundamentos de Métodos de Pesquisa em Administração. São
Paulo: Bookman, 2010.
25.KOLMOGOROV, A. "Sulla determinazione empirica di una legge di
distribuzione" G. Inst. Ital. Attuari, 4, 83,1933
26.KUTNER, MICHAEL; NETER, JOHN; NACHTSHEIM, CHRISTOPHER
288

J.; LI, WILLIAN. Applied Linear Statistical Models. 5. ed. New York:
McGraw-Hill/Irwin, 2004.
27.LARSON, RON.; FARBER, BETSY. Estatística Aplicada. São Paulo.
Pearson Prentice Halll, 2004.
28.LEVINE, DAVID M.; BERENSON, MARK L.. Estatística: Teoria e
Aplicações Usando Microsoft Excel em Português. Rio de Janeiro. Livros
Técnicos e Científicos S.A, 2000.
29.MAGALHÃES, M.N ; LIMA, A.C.P DE- Noções de Probabilidade e Estatística.
5ed...SãoPaulo: Ed. Edusp,2005.
30. MOORE, DAVID S. A Estatística Básica e Sua Prática. Tradução: Cristiana Filizola
CarneiroPessoa.3ed. RiodeJaneiro:LTC,2005.
31.MORETTIN, LUIZ GONZAGA. Estatística Básica. Volumes 1 e 2. São
Paulo. Perarson Makron Books, 2000.
32.MORETTIN, PEDRO A; TOLOI, CLÉLIA M. Séries Temporais. São
Paulo. 2. Ed. Editora Atual, 1987.
33.NETER, J., KUTNER, M.H., NACHTSHEM, C.J., WASSERMAN, W. – Applied
Linear Regression Models. 3 ed., Irwin, 1996.
34. OLIVEIRA, FRANCISCO ESTEVAM MARTINS. Estatística e Probabilidades. São
Paulo. Editora Atlas, 1999.
35.PESARAN, H. M and B. PESARAN. Working with Microfit 4.0:
Interactive Economteric Analysis. London: Oxford University Press,1997.
36.PESARAN, H; SHIN, Y. and SMITH, R. Bound testing approaches to
the analysis of level relationships. Journal of Applied E conometrics.16,
289-326, 2001.
37.PESARAN, H; SHIN, Y. and SMITH, R. Bound testing approaches to
the analysis of level relationships. University of Cambridge, Revised-
DAE Working,2000.
38.ROSS, Sheldon. A First Course in Probability. 7. ed. New Jersey:
Prentice Hall,2005.
39.ROSS, Sheldon. Introduction to Probability Models. 9. ed. New York:
Academic Press,2006.
289

40.SIEGEL, SIDNEY. Nonparametric Statistic for the Behavioral Sciences.
USA: McGraw-Hill,1956.
41.SILVA, Nilza Nunes. Amostragem Probabilística. 1. ed. São Paulo:
Edusp,1997.
42.SMAILES, JOANNE; McGrane, ANGELA. Estatística Aplicada à
Administração com Excel. São Paulo. Editora Atlas, 2002
43.VIEIRA, Sônia. Bioestatística-Tópicos Avançados. 2. ed. Rio de Janeiro:
Campus Elsevier, 2004.
44.VIEIRA, Sônia. Estatística para a qualidade. Rio de Janeiro: Campus
Elsevier,1999.
45.VIEIRA, Sônia. Análise da Variância(ANOVA). São Paulo. Editora Atlas,
2006.
46.SMIRNOV, N.V. "Tables for estimating the goodness of fit of empirical
distributions", Annals of Mathematical Statistic, 19, 279, 1948.
290

Curso de estatística básica

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Curso de estatística básica

Último

Curso de estatística básica