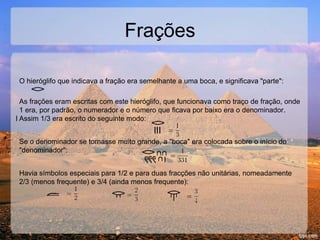
O sistema numérico egípcio era um dos primeiros sistemas a se desenvolver, datando de 3400 a.C. Ele usava hieróglifos para representar números de forma aditiva em uma base 10. Os egípcios registravam matemática e cálculos em papiros importantes como o Papiro de Rhind.

2. INTRODUÇÃO
O tema do meu trabalho é Sistema de Numeração Egípcia,
usado no antigo Egito.
Talvez seja o mais antigo ( 3400 a.C.) sistema de
numeração a se desenvolver;
Era um sistema de numeração em que usavam símbolos
(hieróglifos)
Usava sistema de agrupamento simples (base 10).
Quase tudo o que sabemos sobre a Matemática dos antigos
egípcios se baseia em dois grandes papiros: o Papiro
Ahmes(ou papiro de Rhind) e o Papiro de Moscou.

3. O papiro de Ahme foi escrito por
volta de 1.650 a.C. e tem
aproximadamente 5,5 m de
comprimento e 32 cm de largura.
Foi comprado em 1858 por um
antiquário escocês chamado
Henry Rhind. Por isso é
conhecido também como Papiro
de Rhind. Atualmente encontra-
se no British Museum, de
Londres.
INTRODUÇÃO (cont)
Uma parte do papiro de Rhind.

4. DESENVOLVIMENTO
No sistema de numeração egípcia os números são representados por
símbolos especiais para 1, 10, 100, 1000 e de uma forma aditiva:
• 1 era representado por uma marca que se parecia com um bastão | ;
• 2 era representado por duas marcas || ;
• E assim por diante...até chegar ao 9
• Quando chegavam a 10, eles trocavam as 10 marcas, ( |||||||||| ) por
, que indicava o agrupamento.
• O 11 repetiam I; até 19 - IIIIIIIII
• Para o 20 usavam e assim por diante até ao 90
• Para o 100 já usavam outro símbolo a corda enrolada , repetiam até
ao 900
• O 1000 era representado pela flor de lótus
• 10000 um dedo dobrado
• 100000 um girino e 1000000 um homem

5. DESENVOLVIMENTO(Cont.)
Para facilitar a escrita dos
algarismos hieroglíficos, detalhada
e essencialmente decorativa, foi
encontrado um sistema mais
simples e rápido: os algarismos
hieráticos.

6. Como calculavam os egípcios
• Adição
• Para somar dois números, representavam-nos em separado e, posteriormente,
agrupavam os algarismos da mesma ordem de grandeza. De seguida, cada vez que
tivessem dez símbolos da mesma espécie, substituíam-nos pelo algarismo da
grandeza imediatamente superior, conforme ilustra o seguinte exemplo:
1 729
9 20 700 1 000
+696
6 90 600
=2 425
5 20 400 2 000

7. Como calculavam os egípcios
• Multiplicação
• Para multiplicar dois números, consideravam-se três casos:
• Multiplicação por múltiplos de 10 ,Substituíam cada símbolo pelo símbolo
correspondente ao algarismo da ordem de grandeza seguinte vejamos o caso da
multiplicação de 1464 por 10:
4 60 400 1 000
40 600 4 000 10 000

8. Como calculavam os egípcios
Multiplicação por potências de 2
• Os egípcios, formavam duas colunas e numa
delas colocavam o número 1 seguido das suas
sucessivas multiplicações por 2, até ao número
(por exemplo 256). Na segunda coluna
colocavam o número b (por exemplo 15) e
procediam de modo análogo, efectuando o
mesmo número de multiplicações necessárias
para chegar ao a na primeira coluna. O resultado
do produto seria o último número obtido na
segunda coluna.
• Vejamos o seguinte exemplo, que ilustra a
multiplicação de 15 por 256, cujo resultado será
3840.
1 15
2 30
4 60
8 120
16 240
32 480
64 960
128 1920
256 3840

9. Como calculavam os egípcios
• Multiplicação por números que não são potências de 2 nem múltiplos de 10:
1 11
2 22
— 4 44 /
— 8 88 /
— 16
17
6
/
32
35
2
— 64
70
4
/
Como no caso anterior, formavam duas colunas e, numa delas, colocavam o
número 1 seguido das sucessivas multiplicações por 2, até à primeira potência
inferior a a (por exemplo 92) Na segunda coluna colocavam o número b (por
exemplo 11) e procediam de modo análogo, efectuando o mesmo número de
multiplicações necessárias para chegar ao a na primeira coluna.
Posteriormente procuravam e assinalavam com um pequeno traço horizontal
os números da primeira coluna cuja soma era a( 4+8+16+64 = 92). Somando os
números correspondentes a esses na segunda coluna (que eram marcados
com um traço oblíquo) (44+88+176+704 =1012)obtinham o resultado
pretendido.
Exemplo: Multiplicação de 92 por 11
92×11= 44+88+176+704

10. Como calculavam os egípcios
• Divisão por números que não são potências de 2 nem múltiplos de 10:
O processo é idêntico, uma vez que vamos ter novamente duas
colunas mas, desta vez, a primeira coluna a ser preenchida é a
segunda, onde colocavam o divisor (por exemplo 17) e as
sucessivas multiplicações por 2, até esse produto ser o maior
número inferior ao dividendo. Na primeira coluna colocavam o
número 1 e as sucessivas multiplicações por 2, tantas vezes
quantas as utilizadas nas coluna 2. Posteriormente procuravam e
assinalavam com um pequeno traço horizontal os números da
segunda coluna cuja soma era o dividendo (por exemplo
4556). Somando os números correspondentes a esses na primeira
coluna (que eram marcados com um traço oblíquo) obtinha-se o
resultado pretendido.
Exemplo: Divisão de 4556 por 17
1 17
2 34
— 4 68 /
— 8 136 /
16 272
32 544
64
108
8
128
217
6
— 256
435
2
/

11. Frações
O hieróglifo que indicava a fração era semelhante a uma boca, e significava "parte":
As frações eram escritas com este hieróglifo, que funcionava como traço de fração, onde
1 era, por padrão, o numerador e o número que ficava por baixo era o denominador.
Assim 1/3 era escrito do seguinte modo:
III
Se o denominador se tornasse muito grande, a "boca" era colocada sobre o início do
"denominador":
Havia símbolos especiais para 1/2 e para duas fracções não unitárias, nomeadamente
2/3 (menos frequente) e 3/4 (ainda menos frequente):

12. Dada uma fracção ímpar, fracção unitária de denominador ímpar, para
calcular 2/3 dessa fracção, dever-se-ia multiplicar a fracção por 1/2 e
por 1/6 e somar esses valores, por exemplo, 2/3 de 1/11 seria feito
desta forma;
2/3 x 1/11 = 1/2 x 1/11 + 1/6 x 1/11 = 1/22 + 1/66.
Isto tem origem no facto de nas matemática do Antigo Egito apenas se
efetuarem operações aritméticas com fracções unitárias e de 2/3 = 1/2
+ 1/6.
Para fracções pares, a regra traduz-se em adicionar ao denominador
metade de si mesmo, por exemplo;
2/3 x 1/10 = 1/ (10 + 5) = 1/15
Frações (exemplo)

13. Geometria
Muitos dos problemas que foram decifrados mostram cálculos de áreas, volumes ou
medições relativas à inclinação das pirâmides.
Algumas unidades usadas pelos egípcios:
Côvado - Era baseado no comprimento do antebraço, da ponta do dedo médio até o
cotovelo. O côvado real ou cubito dos antigos egípcios media 50cm. Aqui representado
pelo nº 4.
• 1 côvado = 28 dígitos equivalente a três palmos, ou 66 centímetros.
Seked -era uma unidade de medida egípcia para a medir superfícies inclilinadas.

14. Seked
O sistema foi baseado na medida linear do egípcio conhecido como o cúbito real.
O côvado real foi subdividido em sete palmas e cada palma foi dividido em quatro dedos.
A inclinação dos taludes medidos foi, portanto, expressa como o número de palmas e
dedos movidos horizontalmente para cada aumento cúbito real.
Como podem reparar temos 5 palmos
e meio como um palmo tem 4 dedos
meio palmo tem 2
5 palmos 2 dedos

15. Conclusão
Gostei de fazer este trabalho fiquei a saber
muito sobre este tema.
E população egípcia na parte seu sistema
numeração soma multiplicação e divisão.
Fim