Transferir como PDF, PPTX
Carregado porPedro Santos
Canhao eletrons ime
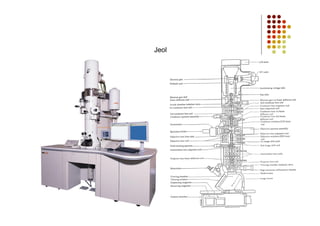
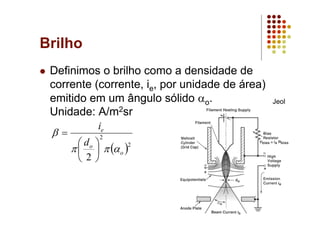
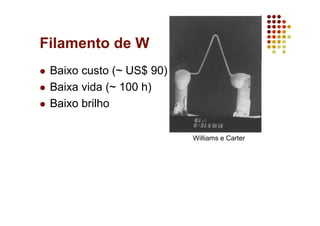
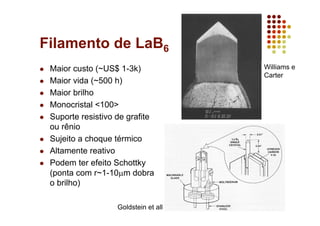
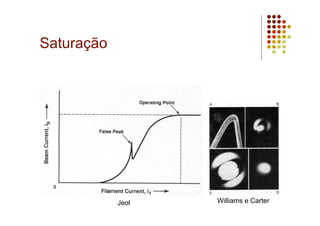
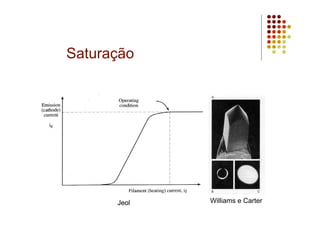
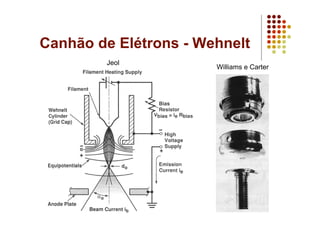
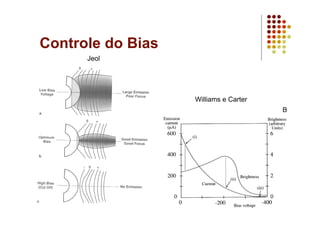
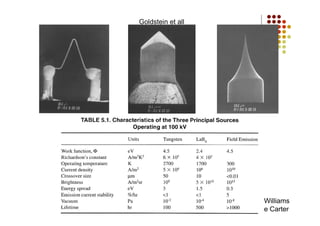
O documento discute as características e vantagens dos canhões de emissão de campo (FEG) em microscópios eletrônicos em comparação com fontes termiônicas convencionais. Os FEG fornecem maior brilho, coerência, estabilidade e vida útil, além de resolução de energia superior. Eles permitem obter imagens de alta resolução com detalhes atômicos devido à sua alta coerência espacial e temporal.
Canhao eletrons ime
- 1. Canhões de Elétrons AndréLuiz Pinto, DC Chefe do Laboratório de Microscopia Eletrônica do IME
- 2.
- 3. Canhão de Elétrons ZrO/W(100)Schottky Type Electron Gun Higher brightness, 100 times greater than LaB6 gun Higher coherency Higher energy resolution, 0.7 to 0.8eV Higher stability over a cold FEG Longer life time 1.5 to 3 years (guarantied time: 5,000 hours) Jeol
- 4. O que desejamosem um canhão? Alto brilho Fonte de dimensões reduzidas Estabilidade Energia Controlável Coerência
- 5. Brilho Definimos o brilhocomo a densidade de corrente (corrente, ie, por unidade de área) emitido em um ângulo sólido αo. Unidade: A/m2sr ( )2 2 2 o o e d i αππ β ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = Jeol
- 6. Energia dos Elétrons Atravésdo Princípio da Dualidade Onda- Partícula de de Broglie podemos associar o momento da partícula ao seu comprimento de onda Energia cinética do elétron a partir do seu potencial de aceleração p h =λ eVmvmp vm eV oo o 2 2 2 ==⇒=
- 7. Energia dos Elétrons Comprimentode onda Correção relativística eVm h o2 =λ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + = 2 2 12 cm eV eVm h o o λ
- 8. Fontes Termiônicas Lei deRichardson para a densidade de corrente kT eATJ Φ − = 2 A- Cte de Richardson Φ - Função Trabalho K – Cte de Boltzmann
- 9. Filamento de W Baixocusto (~ US$ 90) Baixa vida (~ 100 h) Baixo brilho Williams e Carter
- 10. Filamento de LaB6 Maiorcusto (~US$ 1-3k) Maior vida (~500 h) Maior brilho Monocristal <100> Suporte resistivo de grafite ou rênio Sujeito a choque térmico Altamente reativo Podem ter efeito Schottky (ponta com r~1-10µm dobra o brilho) Williams e Carter Goldstein et all
- 11.
- 12.
- 13. Canhão de Elétrons- Wehnelt Jeol Williams e Carter
- 14. Controle do Bias Williamse Carter Jeol
- 15. Problemas das Fontes Termiônicas Evaporaçãodo catodo “Thermal drift” Baixo brilho Brilho máximo kT eVJ oc Max π β =
- 16. Canhão de Emissãopor Campo (Field Emission Gun - FEG) Monocristal <310> com ponta afiada (r<100 ηm) Menor raio concentra o campo elétrico e diminui a necessidade de T V1 – voltagem de extração (3-5 kV) V2 – voltagem de aceleração Brilho máximo E eVJ oc Max ∆ = π β Williams e Carter
- 17. Canhão de Emissãopor Campo (Field Emission Gun - FEG) 3 tipos básicos Frio Térmico Schottky Crossover Frio - < 5 ηm Térmico - < 5 ηm Schottky - < 15-30 ηm Variação da Energia (∆E) Frio – 0,3 eV Térmico – 1 eV Schottky – 0,3 - 1 eV Estabilidade Frio – 5%/h Térmico – 5%/h Schottky – 2%/h Goldstein et all
- 18.
- 19.
- 20. Coerência Coerência avalia quão“em fase” estão as ondas de elétrons Coerência temporal Coerência Espacial α - ângulo de convergência FEG possui grande coerência temporal e espacial E vh c ∆ =λ α λ 2 <<cd
- 21. Diâmetro do Feixe Odiâmetro final, dt, é resultado do diâmetro do “crossover” alargado pela aberração esférica da lente objetiva, ds, e a difração pela última abertura, dd. 222 dsgt dddd ++= αβπ 12 2 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = i dg 3 5,0 αss Cd = α λ 22,1=dd
- 22. Referências Williams, D. B.e Carter, C. B., “Transmission Electron Microscopy” , Ed. Plenum, New York, 1996. Goldstein, J. et all, “Scanning Electron Microscopy and X–Ray Analysis”, Ed. Springer, 2003. Apostila da Jeol – MET Apresentação da Jeol – Jeol 2100F