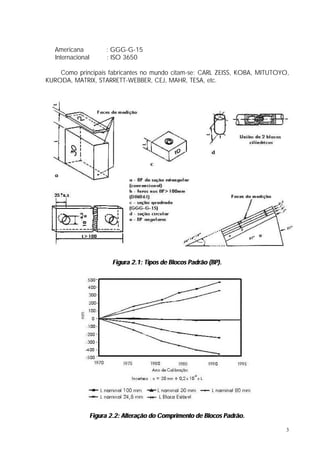
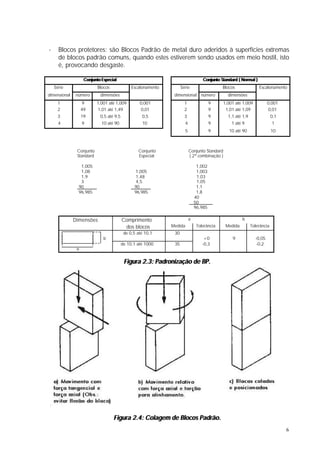
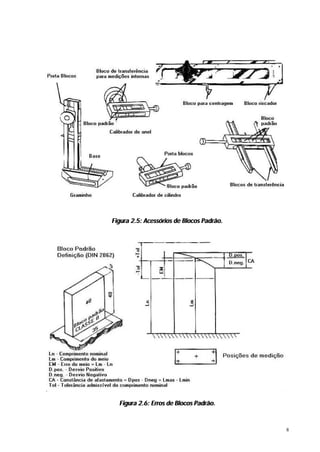
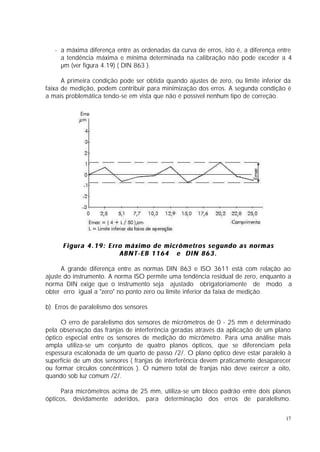
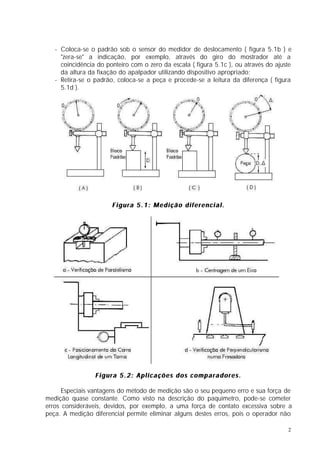
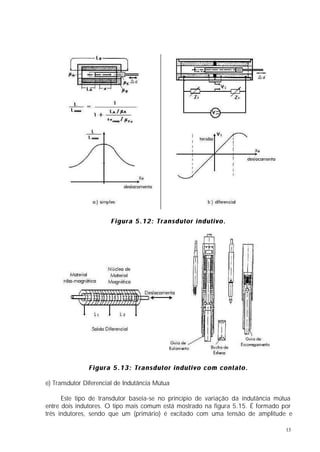
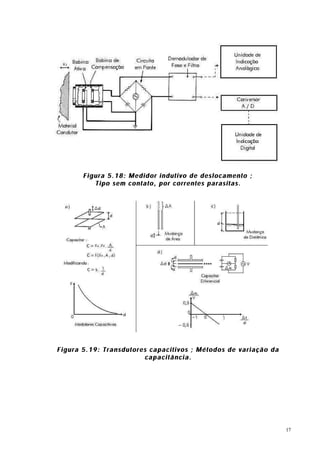
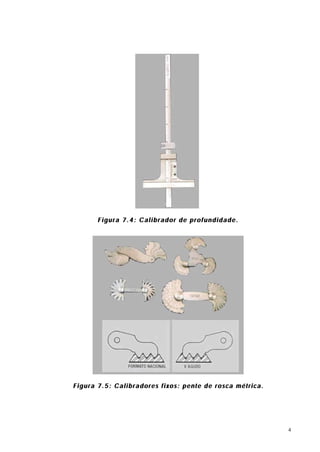
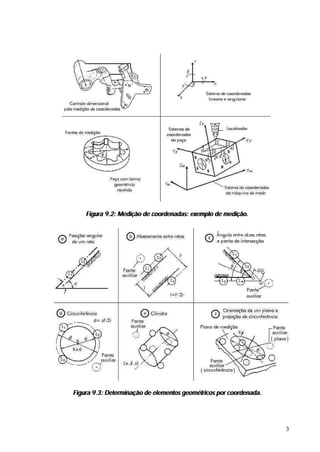
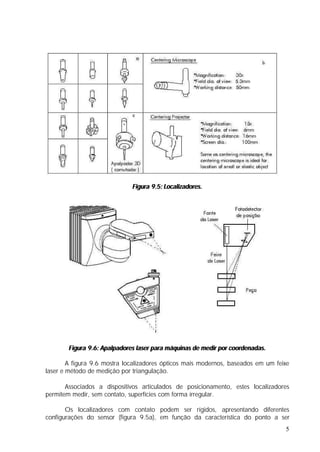
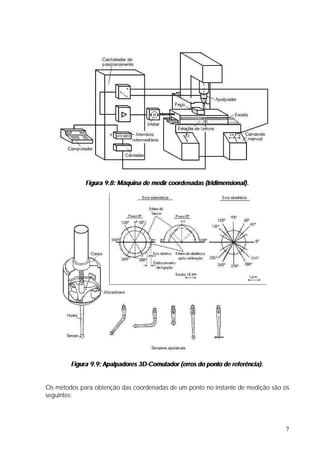
O documento discute controle geométrico e medição dimensional. Aborda conceitos como tolerância geométrica, causas de desvios de forma, medição de comprimento e causas de erros de medição. Também apresenta detalhes sobre blocos padrão, paquímetros, micrômetros e outros instrumentos de medição.

1. PARTE II
METROLOGIA
Prof. Marco Antonio Martins Cavaco
2002 – I
Laboratório de Metrologia e Automatização
Departamento de Engenharia Mecânica
Universidade Federal de Santa Catarina

2. Conteúdo
1 CONTROLE GEOMÉTRICO
1.1 TOLERÂNCIA GEOMÉTRICA
1.1.1 Tolerâncias Dimensionais (Tolerâncias de Fabricação)
1.1.2 Desvios de forma
1.1.2.1 Tolerâncias de Posição
1.1.2.2 Tolerância de orientação
1.1.2.3 Tolerância de forma
1.1.2.4 Tolerância de movimentação
1.1.2.5 Rugosidade
1.1.3 Causas dos desvios de forma
1.2 MEDIÇÃO DE UM COMPRIMENTO
1.3 CONTROLE DE UMA DIMENSÃO
1.4 CAUSAS DE ERROS NAS MEDIÇÕES DE COMPRIMENTO
1.4.1 Fatores de Natureza Mecânica
1.4.2 Fatores de Natureza Geométrica
1.4.2 Fator de Natureza Física
2 BLOCOS PADRÃO
2.1 GENERALIDADES
2.1.1 Definição
2.1.2 Tipos
2.1.3 Fabricação
2.1.4 Normas e Fabricantes
2.1.5 Apresentação – Jogos
2.2 ASPECTOS OPERACIONAIS
2.2.1 Recomendações de Utilização
2.2.2 Composição de Blocos Padrão
2.2.3 Acessórios
2.3 DEFINIÇÃO DE COMPRIMENTO DE UM BLOCO PADRÃO E ERROS
2.3.1 Comprimento de um Bloco Padrão
2.3.2 Caracterização dos Erros
2.4 AS CLASSES DE ERRO E SUAS APLICAÇÕES
2.5 ERRO DE UMA COMPOSIÇÃO DE BLOCOS

3. 2.6 BLOCOS PADRÃO DE CERÂMICA
2.6.1 Resistência a Corrosão
2.6.2 Resistência à Abrasão
2.6.3 Estabilidade Dimensional
2.6.4 Coeficiente de Expansão Térmica, Módulo de Elasticidade, Dureza e
Condutibilidade Térmica
2.6.5 Aderência das Superfícies
2.6.6 Resistência Mecânica a Impactos
2.6.7 Gravações
2.7 MÉTODOS DE CALIBRAÇÃO DE BLOCOS PADRÃO
2.7.1 Método Diferencial
2.7.2 Método Interferométrico
3 PAQUÍMETRO
3.1 ASPECTOS GERAIS
3.1.1 Definição
3.1.2 Características Construtivas
3.1.3 Tipos de Paquímetros
3.1.4 Aspectos Operacionais
3.2 COMPORTAMENTO METROLÓGICO
4 MICRÔMETROS
4.1 INTRODUÇÃO
4.2 PARAFUSOS DE MEDIÇÃO
4.3 MICRÔMETROS
4.3.1 Tipos de Micrômetros
4.3.2 Micrômetros Digitais
4.4 FONTES DE ERROS NAS MEDIÇÕES COM MICRÔMETROS
4.5.1 PROCEDIMENTO DE CALIBRAÇÃO
4.5.1 Cuidados Iniciais
4.5.2 Normas Técnicas
4.5.3 Parâmetros a Serem Qualificados
4.5.4 Intervalos de Calibração
4.6 EXEMPLOS
4.7 REFERÊNCIAS BIBLIOGRÁFICAS
5 MEDIDORES DE DESLOCAMENTO
5.1 INTRODUÇÃO

4. 5.1.1 Importância
5.1.2 Medição Diferencial
5.2 MEDIDORES MECÂNICOS
5.2.1 Sistema de Mola Torcional
5.2.2 Relógios comparadores
5.3 MEDIDORES PNEUMÁTICOS
5.4 ELÉTRICOS ANALÓGICOS
5.4.1 Resistivos
5.4.2 Indutivo
5.4.3 Capacitativo
5.4.4 Fotoelétrico
5.5 MEDIDORES ELÉTRICOS DIGITAIS
5.5.1 Medidores com Escalas Eletroópticas Incrementais
5.5.2 Medidores com Escalas Eletroópticas Absolutas
5.5.3 O Laser Interferométrico
5.6 NORMAS RELATIVAS AOS MEDIDORES DE DESLOCAMENTO
6 INSTRUMENTOS AUXILIARES DE MEDIÇÃO
6.1 MATERIALIZAÇÃO DE FORMAS GEOMÉTRICAS SIMPLES
6.2 DESEMPENOS
6.3 RÉGUAS
6.4 ESQUADROS
7 CALIBRADORES
7.1 INTRODUÇÃO
7.2 CARACTERÍSTICAS DE FABRICAÇÃO
7.3 TIPOS E APLICAÇÕES
7.4 CALIBRADORES FIXOS
7.4.1 Calibradores Tampões
7.4.2 Calibradores Anulares
7.4.3 Calibradores de Boca e Calibradores Planos
7.4.4 Calibradores tipo Haste
7.4.5 Calibradores de Roscas Cilíndricas
7.4.6 Calibradores de Roscas Cônicas
7.5 QUALIFICAÇÃO DE CALIBRADORES

5. 8 MÁQUINAS DE MEDIR
8.1 INTRUDUÇÃO
8.2 MÁQUINA ABBÉ
8.3 MICROSCÓPIOS DE MEDIÇÃO
8.4 PROJETORES DE PERFIL
8.5 MÁQUINAS DEDICADAS
8.6 MESAS DIVISORAS
9 MÁQUINAS DE MEDIR POR COORDENADAS
9.1 IMPORTÂNCIA
9.2 MEDIÇÃO POR COORDENADAS
9.3 CONFIGURAÇÕES MECÂNICAS
9.4 APALPADORES
9.5 ERROS DE MEDIÇÃO
9.6 NÍVEIS DE AUTOMAÇÃO
9.7 ASPECTOS ECONÔMICOS
10 AUTOMAÇÃO DO CONTROLE DIMENSIONAL
10.1 INTRODUÇÃO
10.2 ESTAÇÕES AUTOMÁTICAS DE MEDIÇÃO
10.3 CONTROLE DIMENSIONAL NO PROCESSO
10.3.1 Controle próximo à Unidade de Fabricação
10.3.2 Controle junto à Unidade de Fabricação
10.3.3 Controle dentro da Unidade da Fabricação
10.4 INTEGRAÇÃO DA INFORMAÇÃO
11 MEDIÇÃO DE ROSCAS
11.1 GEOMETRIA DE ROSCAS
11.2 MÉTODOS DE MEDIÇÃO DE ROSCAS
11.2.1 Comparação dos Métodos Ópticos e Mecânicos
11.2.2 Métodos Mecânicos de Medição de Roscas
11.2.3 Método Óptico de Medição de Roscas Externas

6. Capítulo 1
CONTROLE GEOMÉTRICO
O controle geométrico trata basicamente dos procedimentos de determinação de dimensões,
forma e posição de elementos sólidos. Para isto deve-se considerar o comportamento
metrológico do sistema de medição e a condição do objeto a medir.
Deve-se ter em mente que na fabricação de uma peça não se consegue obter a forma
geométrica perfeita, assim ao usinar um cilindro tem-se erros de circularidade na seção
transversal. Se este cilindro foi usinado em um torno comum, um torno de precisão ou uma
retifica, naturalmente e de se esperar que os erros de circularidade sejam, respectivamente, de
valor decrescente. Quanto mais sofisticado o processo de fabricação, menor será o valor da
tolerância de fabricação estipulada para a geometria em questão.
Desse modo, para garantir que os desvios de fabricação não prejudiquem a montagem e o
funcionamento perfeito das peças, o controle geométrico passa a ser necessário e é realizado
através de especificações de tolerâncias geométricas.
1.1 TOLERÂNCIA GEOMÉTRICA
Os desvios geométricos permissíveis para a peça são previamente indicados, aplicando-se
tolerâncias geométricas que são os limites dentro dos quais as dimensões e formas geométricas
possam variar sem que haja comprometimento do funcionamento e intercambiabilidade das
peças.
Tais desvios podem ser macrogeométricos, sendo desvios macroscópicos como retilineidade,
planeza, dimensões nominais e desvios microgeométricos, sendo desvios superficiais
microscópicos como rugosidade e aspereza.
A figura 1.1 ilustra os tipos de tolerâncias que compõem as tolerâncias geométricas.
Tolerâncias Geométricas
Tolerância Dimensional Desvios de Forma
Tolerância Tolerância Tolerância Tolerância Tolerância
de de de de de Rugosidade
Orientação Localização Movimento Forma Ondulação
Figura 1.1 – Quadro geral das Tolerâncias Geométricas.
1

7. 1.1.1 Tolerâncias Dimensionais (Tolerâncias de Fabricação)
Os limites de erros (tolerâncias dimensionais) que uma peça pode apresentar em sua
geometria, são estabelecidos pelo projetista da mesma, em função da aplicação prevista para
a peça.
A determinação destas tolerâncias é um problema de projeto mecânico e não será abordado
neste curso. Esta determinação exige grande experiência e/ou o conhecimento de
procedimentos normalizados.
Existem sistemas de tolerância e ajustes normalizados para os elementos geométricos
rotineiramente utilizados, como: elementos unidimensionais (eixo/furo, cones, parafuso/rosca,
engrenagens, etc.
A seguir, serão apresentados alguns conceitos sobre as tolerâncias dimensionais do sistema
eixo/furo:
• Dimensão nominal (D ou d): dimensão teórica indicada no desenho ou projeto.
• Dimensão efetiva (De ou de): dimensão real da peça obtida através de instrumentos de
medição.
• Linha zero (Lz): nos desenhos de peças que se faz necessária a indicação dos limites
permissíveis para a dimensão efetiva, indica-se linha zero, que é uma linha tracejada,
colocada exatamente na posição correspondente à dimensão nominal.
• Dimensão máxima (Dmax ou dmax): dimensão máxima permitida para a dimensão efetiva sem
que a peça seja rejeitada.
• Dimensão mínima (Dmin ou dmin): dimensão mínima permitida para a dimensão efetiva sem
que a peça seja rejeitada.
• Afastamento superior (A S ou aS): diferença entre a dimensão máxima e a dimensão nominal.
AS = DMAX - D (para furos) e aS = dMAX - d (para eixos)
• Afastamento inferior (A i ou ai): diferença entre a dimensão mínima e a dimensão nominal.
Ai = DMIN - D (para furos) e Ai = dMIN - d (para eixos)
• tolerância dimensional (t): variação permissível da dimensão, podendo ser dada pela
diferença entre as dimensões máxima e mínima ou pela diferença entre os afastamentos
superior e inferior.
t = dMAX – dMIN ou t = DMAX – DMIN
t = as – a i ou t = As - Ai
2

8. ai
as
t
As
Ai
Linha zero
t
dimensão
nominal
eixo furo
Figura 1.2 – Esquema dos afastamentos superiores e inferiores (eixos e furos).
Os afastamentos superiores e inferiores podem ser positivos ou negativos. Quando a dimensão
máxima ou mínima está acima da linha zero, o afastamento correspondente é positivo; caso a
dimensão máxima ou mínima esteja abaixo da linha zero, o afastamento é negativo.
O sistema de tolerâncias e ajustes para eixo/furo, por exemplo, prevê 18 níveis de qualidade.
Escolhido o nível de qualidade a ser adotado na fabricação de um elemento da peça, a
tolerância dimensional pode ser obtida pelo quadro da Tabela 1.1, em função do grupo de
dimensão em que se enquadra.
Exemplo: Um eixo de 48 mm de diâmetro, qualidade 7, terá uma tolerância de fabricação de
25 µm.
A posição do campo de tolerância em relação a dimensão nominal (para mais, para menos,
distribuído em relação ao mesmo ou outro) é um problema de ajuste, isto é, diz respeito ao tipo
de encaixe que deverá ser assegurado.
O posicionamento do campo de tolerância para os diferentes ajustes, pode ser obtido a partir
da tabela da Tabela 1.2.
ExempIos: 1) O eixo com ajuste 48 g7, terá como limites de dimensão:
48,000 - 0,009 mm
- 0,034 mm, isto é,
diâmetro mínimo: 47,966 mm
diâmetro máximo: 47,991 mm
2) Eixo com ajuste 48 p7:
48,000 + 0,051 mm
+ 0,026 mm, isto é,
diâmetro mínimo: 48,051 mm
diâmetro máximo: 48,026 mm
3

9. Grupos de
(µ
Qualidade IT (µm)
dimensões
mm 01 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
≥1 0.3 0.5 0.8 1.2 2.0 3 4 6 10 14 25 40 60
> 1≤3 0.3 0.5 0.8 1.2 2.0 3 4 6 10 14 25 40 60 100 140 250 400 600
> 3≤6 0.4 0.6 1.0 1.5 2.5 4 5 8 12 18 30 48 75 120 180 300 480 750
> 6 ≤ 10 0.4 0.6 1.0 1.5 2.5 4 6 9 15 22 36 58 90 150 220 360 580 900
> 10 ≤ 18 0.5 0.8 1.2 2.0 3.0 5 8 11 18 27 43 70 110 180 270 430 700 1100
> 18 ≤ 30 0.6 1.0 1.5 2.5 4 6 9 13 21 33 52 84 130 210 330 520 840 1300
> 30 ≤ 50 0.6 1.0 1.5 2.5 4 7 11 16 25 39 62 100 160 250 390 620 1000 1600
> 50 ≤ 80 0.8 1.2 2.0 3 5 8 13 19 30 46 74 120 190 300 460 740 1200 1900
> 80 ≤ 120 1.0 1.5 2.5 4 6 10 15 22 35 54 87 140 220 350 540 870 1400 2200
> 120 ≤ 180 1.2 2.0 3.5 5 8 12 18 25 40 63 100 160 250 400 630 1000 1600 2500
> 180 ≤ 250 2.0 3.0 4.5 7 10 14 20 29 46 72 115 185 290 460 720 1150 1850 2700
> 250 ≤ 315 2.5 4 6 8 12 16 23 32 52 81 130 210 320 520 810 1300 2100 3200
> 315 ≤ 400 3 5 7 9 13 18 25 36 57 89 140 230 360 570 890 1400 2300 3600
> 400 ≤ 500 4 6 8 10 15 20 27 40 63 97 155 250 400 630 970 1550 2500 4000
Tabela 1.1 – Qualidade de fabricação IT e grupos de dimensões.
O ajuste é o acoplamento de dois elementos com a mesma dimensão nominal caracterizando-
se pelas tolerâncias adotadas, grau de acabamento exigido para a execução das peças e pela
diferença das dimensões efetivas do eixo e furo.
Existem três condições de ajuste:
• com folga: são aqueles que sempre apresentam um jogo efetivo entre os elementos, de
forma que o eixo pode girar ou deslizar dentro do furo.
• com Interferência: são aqueles que sempre apresentam uma resistência ao acoplamento,
caracterizando-se pela dimensão mínima do eixo superior à dimensão máxima do furo.
• incertos: entre dois elementos a serem acoplados, poderá existir uma interferência ou folga
conforme as dimensões efetivas das peças, as quais devem manter-se entre os limites
impostos. Para que ocorra o ajuste incerto, a dimensão máxima do furo é superior à
dimensão máxima do eixo, enquanto que a dimensão mínima do furo é inferior à dimensão
máxima do eixo.
Outros elementos geométricos caracterizados por duas ou mais dimensões tem seus próprios
sistemas de tolerância e ajuste.
Exemplo: - Cones : (DIN 229)
- Roscas : (DIN 13)
4

10. Grupo Posição
de
dimensões j5 k4 k<3
mm a b c cd d e ef f fg g h js j7 j8 m n p r s t u v x y z za zb zc
j6 a k>7
k7
0a1 -60 -34 -20 -14 -10 -6 -4 -2 0 -2 -4 -6 0 0 2 4 6 10 14 18 20 26 32 40 60
>1≤3 -270 -140 -60 -34 -20 -14 -10 -6 -4 -2 0 -2 -4 1 0 2 4 6 10 14 18 20 26 32 40 60
>3≤6 -270 -140 -70 -46 -30 -20 -14 -10 -6 -4 0 -2 -4 1 0 4 8 12 15 19 23 28 35 42 50 80
> 6 ≤ 10 -280 -150 -80 -56 -40 -25 -18 -13 -8 -5 0 -2 -5 1 0 6 10 15 19 23 28 34 42 52 67 97
> 10 ≤ 14 -290 -150 -95 -50 -32 -16 -6 0 -3 -6 1 0 7 12 18 23 28 33 40 50 64 90 130
> 14 ≤ 18 -290 -150 -95 -50 -32 -16 -6 0 -3 -6 1 0 7 12 18 23 28 33 39 45 60 77 108 150
> 18 ≤ 24 -300 -160 -110 -65 -40 -20 -7 0 -4 -8 2 0 8 15 22 28 35 41 47 54 63 73 98 136 188
> 24 ≤ 30 -300 -160 -110 -65 -40 -20 -7 0 -4 -8 2 0 8 15 22 28 35 41 48 55 64 75 88 118 160 218
> 30 ≤ 40 -310 -170 -120 -80 -50 -25 -9 0 -5 -10 2 0 9 17 26 34 43 48 60 68 80 94 112 148 200 274
> 40 ≤ 50 -320 -180 -130 -80 -50 -25 -9 0 -5 -10 2 0 9 17 26 34 43 54 70 81 97 114 136 180 242 325
> 50 ≤ 65 -340 -190 -140 -100 -60 -30 -10 0 -7 -12 2 0 11 20 32 41 53 66 87 102 122 144 172 226 300 405
> 65 ≤ 80 -360 -200 -150 -100 -60 -30 -10 0 -7 -12 2 0 11 20 32 43 59 75 102 120 146 174 210 274 360 480
> 80 ≤ 100 -380 -220 -170 -120 -72 -36 -12 0 -9 -15 3 0 13 23 37 51 71 91 124 146 178 214 258 335 445 585
> 100 ≤ 120 -410 -240 -180 -120 -72 -36 -12 0 -9 -15 3 0 13 23 37 54 79 104 144 172 210 254 310 400 525 690
> 120 ≤ 140 -460 -260 -200 -145 -85 -43 -14 0 -11 -18 3 0 15 27 43 63 92 122 170 202 248 300 365 470 620 800
> 140 ≤ 160 -520 -280 -210 -145 -85 -43 -14 0 -11 -18 3 0 15 27 43 65 100 134 190 228 280 340 415 535 700 900
> 160 ≤ 180 -580 -310 -230 -145 -85 -43 -14 0 -11 -18 3 0 15 27 43 68 108 146 210 252 310 380 465 600 780 1000
> 180 ≤ 200 -660 -340 -240 -170 -100 -50 -15 0 -13 -21 4 0 17 31 50 77 122 166 236 284 350 425 520 670 890 1150
> 200 ≤ 225 -740 -380 -260 -170 -100 -50 -15 0 -13 -21 4 0 17 31 50 80 130 180 258 310 385 470 575 740 960 1250
> 225 ≤ 250 -820 -420 -280 -170 -100 -50 -15 0 -13 -21 4 0 17 31 50 84 140 196 284 340 425 520 640 820 1050 1350
> 250 ≤ 280 -920 -480 -300 -190 -110 -56 -17 0 -16 -26 4 0 20 34 56 94 158 218 315 385 475 580 710 920 1200 1550
> 280 ≤ 315 -1050 -540 -330 -190 -110 -56 -17 0 -16 -26 4 0 20 34 56 98 170 240 350 425 525 650 790 1000 1300 1700
> 315 ≤ 355 -1200 -600 -360 -210 -125 -62 -18 0 -18 -28 4 0 21 37 62 108 190 268 390 475 590 730 900 1150 1500 1900
> 355 ≤ 400 -1350 -680 -400 -210 -125 -62 -18 0 -18 -28 4 0 21 37 62 114 208 294 435 530 660 820 1000 1300 1650 2100
> 400 ≤ 450 -1500 -760 -440 -230 -135 -68 -20 0 -20 -32 5 0 23 40 68 126 232 330 490 595 740 920 1100 1450 1850 2400
> 450 ≤ 500 -1650 -840 -480 -230 -135 -68 -20 0 -20 -32 5 0 23 40 68 132 252 360 530 660 820 1000 1250 1600 2100 2600
Tabela 1.2 – Valores de afastamentos de referência para eixos ( µm).
Observações:
• Para eixos com ajustes de “a até j”, os afastamentos da tabela são superiores, de “j até zc” são inferiores.
• Para furos, os afastamentos são iguais aos valores negativos dos tabelados.
• Para furos com ajustes de “A até H”, os afastamentos da tabela são inferiores, de “J até ZC” são inferiores.
5

11. 1.1.2 Desvios de forma
1.1.2.1 Tolerâncias de Posição
Fig. 1.3 – Tolerâncias de Posição – simbologia.
• Tolerância de posição: definida como desvio tolerado de um determinado elemento (ponto,
reta, plano) em relação a sua posição teórica.
Fig. 1.4 – Tolerância de posição – especificação em desenho e interpretação.
• Tolerância de simetria: o campo de tolerância é limitado por duas retas paralelas, ou por dois
planos paralelos, distantes no valor especificado e dispostos simetricamente em relação ao
eixo (ou plano) de referência.
Fig. 1.5 – Tolerância de simetria – especificação em desenho e interpretação.
6

12. • Tolerância de concentricidade: define-se concentricidade como a condição segundo a qual os
eixos de duas ou mais figuras geométricas, tais como cilindros, cones etc., são coincidentes.
Fig. 1.6 – Tolerância de concentricidade – especificação em desenho e interpretação.
1.1.2.2 Tolerância de orientação
Fig. 1.7 – Tolerâncias de orientação – simbologia.
• Tolerância de paralelismo: é a condição de uma linha ou superfície ser equidistante em
todos os seus pontos de um eixo ou plano de referência.
Fig. 1.8 – Tolerância de paralelismo – especificação em desenho e interpretação.
7

13. • Tolerância de perpendicularidade: é a condição pela qual o elemento deve estar dentro do
desvio angular, tomado como referência o ângulo reto entre uma superfície, ou uma reta, e
tendo como elemento de referência uma superfície ou uma reta, respectivamente.
Fig. 1.9 – Tolerância de perpendicularidade – especificação em desenho e interpretação.
• Tolerância de inclinação: o campo de tolerância é limitado por dois planos paralelos, cuja
distância é o valor da tolerância, e inclinados em relação à superfície de referência do ângulo
especificado.
Fig. 1.10 – Tolerância de inclinação – especificação em desenho e interpretação.
1.1.2.3 Tolerância de forma
Fig. 1.11 - Tolerâncias de forma – simbologia.
8

14. • Tolerância de retilineidade: é a condição pela qual cada linha deve estar limitada dentro do
valor de tolerância especificada.
Fig. 1.12 – Tolerância de retilineidade – especificação em desenho e interpretação.
• Tolerância de planeza: é a condição pela qual toda superfície deve estar limitada pela zona
de tolerância “t”, compreendida entre dois planos paralelos, distantes de “t”.
Fig. 1.13 – Tolerância de planeza – interpretação.
• Tolerância de circularidade: condição pela qual qualquer círculo deve estar dentro de uma
faixa definida por dois círculos concêntricos, distantes no valor da tolerância especificada.
Fig. 1.14 – Tolerância de circularidade.
9

15. • Tolerância de forma de superfície: o campo de tolerância é limitado por duas superfícies
envolvendo esferas de diâmetro igual à tolerância especificada e cujos centros estão situados
sobre uma superfície que tem a forma geométrica correta.
Fig. 1.15 – Tolerância de forma de superfície – especificação em desenho e interpretação.
• Tolerância de cilindricidade: é a condição pela qual a zona de tolerância especificada é a
distância radial entre dois cilindros coaxiais.
Fig. 1.16 – Tolerância de forma de cilindricidade – especificação em desenho e interpretação.
1.1.2.4 Tolerância de movimentação
• Tolerância de batimento radial: é definida como um campo de distância t entre dois círculos
concêntricos, medidos em um plano perpendicular ao eixo considerado.
• Tolerância de batimento axial: é definida como o campo de tolerância determinado por duas
superfícies, paralelas entre si e perpendiculares ao eixo de rotação da peça, dentro do qual
deverá estar a superfície real quando a peça efetuar uma volta, sempre referida a seu eixo de
rotação.
10

16. Fig. 1.17 – Tolerância de batimento radial e axial.
1.1.2.5 Rugosidade
É o conjunto de irregularidades, isto é, pequenas saliências e reentrâncias que caracterizam uma
superfície. Essas irregularidades podem ser avaliadas com aparelhos eletrônicos, a exemplo do
rugosímetro. A rugosidade desempenha um papel importante no comportamento dos
componentes mecânicos. Ela influi na:
• qualidade de deslizamento;
• resistência ao desgaste;
• transferência de calor;
• qualidade de superfícies de padrões e componentes ópticos;
• possibilidade de ajuste do acoplamento forçado;
• resistência oferecida pela superfície ao escoamento de fluidos e lubrificantes;
• qualidade de aderência que a estrutura oferece às camadas protetoras;
• resistência à corrosão e à fadiga;
• vedação;
• aparência.
O parâmetro de rugosidade mais usado baseia-se nas medidas de profundidade da rugosidade.
Ra é a média aritmétrica dos valores absolutos das ordenadas do perfil efetivo em relação à linha
média num comprimento de amostragem. Pode ser calculado da seguinte forma:
1 L A
L ∫
Ra = ⋅ y ⋅ dx ou Ra =
0 Lc
onde: A = média da soma das áreas acima e abaixo da linha média;
Lc = comprimento analisado para a obtenção de A.
11

17. Fig. 1.18 – Rugosidade: ilustração esquemática para obtenção de Ra.
a
1.1.3 Causas dos desvios de forma
Os desvios de forma que afetam as dimensões nominais das peças podem ser ocasionados por
diversos fatores, sendo os principais (conhecidos por 6M) listados a seguir:
• material da peça: usinabilidade, conformabilidade ou dureza;
• meio de medição: incerteza de medição, adequação do instrumento ao mensurando;
• máquina-ferramenta: ferramenta de corte, defeitos nas guias, erros de posicionamento;
• mão de obra: erros de interpretação, falta de treinamento;
• meio ambiente: variação de temperatura, limpeza do local de trabalho;
• método: processo de fabricação para obtenção da peça, parâmetros de corte.
1 . 2 MEDIÇÃO DE UM COMPRIMENTO
Na determinação de um comprimento ou de um ângulo de uma peça, procede-se da mesma
forma como na determinação de qualquer outra grandeza física, para se alcançar a resultado da
medição.
Segue-se aqui as orientações dada no capítulo 7 da apostila 1 de metrologia e controle
geométrico, considerando-se, adicionalmente, as fontes de erro ligados a medição de
comprimentos a serem analisados neste capitulo.
Caso o problema a ser resolvido é saber se a peca se enquadra nos limites de tolerância
especificados no projeto, o encaminhamento do problema é distinto. Trata-se da execução de um
controle dimensional.
1 . 3 CONTROLE DE UMA DIMENSÃO
Após a fabricação das peças inicia-se o trabalho do metrologista, ou seja, realizar a verificação
se as peças produzidas tem dimensões dentro das especificações do projeto. Nesta verificação a
12

18. peça será classificada como boa ou refugo.
A partir do valor da tolerância de fabricação (IT ou t), especifica-se qual o máximo erro admissível
que pode ocorrer na medição da grandeza em questão.
A relação entre a incerteza de medição do processo de medição, no controle do diâmetro de
determinado eixo, e a faixa de tolerância do mesmo é mostrada na figura 1.19
Para efeito de aprovação ou rejeição da peça toma-se simplesmente a indicação dada pelo
sistema de medição utilizado no processo de medição. Pelo fato da incerteza de medição ser um
décimo do intervalo de tolerância IT, considera-se o processo de medição como perfeito.
No entanto nem sempre dispomos de um processo de medição cuja incerteza de medição é
inferior a um décimo do intervalo de tolerância.
Rejeição Dúvida Aprovação Dúvida Rejeição
LIT LST
- USM + USM valor nominal
tolerância
Fig. 1.19 - Controle de uma dimensão.
Legenda:
LIT: limite inferior da tolerância
LST: limite superior da tolerância
USM : incerteza do sistema de medição
Conforme demonstra a figura 1.19 é possível acontecer 4 casos diferentes de resultado da
medição (resultado corrigido e incerteza associada) em relação aos limites de tolerância.
No primeiro caso (quadrado na figura 1.19), sentido da esquerda para direita, é possível
afirmarmos que o produto deve ser refugado pois o resultado de medição apresenta-se
integralmente fora dos limites de tolerância.
13

19. Já no segundo caso (círculo), o resultado corrigido do processo de medição está dentro do limite
especificado para a tolerância do produto. No entanto, devido a incerteza de medição, está
numa região de dúvida deste limite. Neste caso não é possível afirmar com segurança que o
produto está dentro de tolerância para a dimensão medida. É possível afirmar somente que existe
grande probabilidade do mesmo apresentar-se dentro dos limites de tolerância.
No terceiro caso (cruz) da figura 1.19, o resultado corrigido e a incerteza associada estão dentro
do limite de tolerância. Nesta situação podemos afirmar com segurança que o produto atende as
especificações com relação a tolerância de fabricação.
No quarto caso (triângulo), o resultado corrigido do processo de medição está acima do limite
superior de tolerância do produto. Neste caso não é possível afirmar com segurança que o
produto está fora de tolerância para a dimensão medida, isto é, que o mesmo deveria ser
refugado. Isto porque a incerteza do sistema de medição está abrangendo o valor da medida,
caracterizando uma região de dúvida acerca dos resultados dentro dessa faixa de valores. É
possível afirmar somente que existe grande probabilidade do mesmo apresentar-se fora dos
limites de tolerância.
1.4 CAUSAS DE ERROS NAS MEDIÇÕES DE COMPRIMENTO
1.4.1 Fatores de Natureza Mecânico
a) Força de Medição
Na maioria dos casos o processo de medição a realização da medição, está associado a um
contato mecânico entre os sensores do SM (apalpadores) e o objeto a medir. No caso de
medição por processo óptico, eletroindutivo ou eletrocapacitivo não há contato mecânico direto e
inexiste a força de medição.
Ao contato mecânico está associada uma força, denominada força de medição. Uma certa força
é necessária para que o apalpador possa penetrar (ou deslocar para o lado) camadas de sujeira,
de óleo, de graxa, de gases aderentes e semelhantes que aderem nas superfícies de contato.
Por outro lado, a força de medição provoca no objeto, bem como no sistema de medição e
demais componentes mecânicos utilizados no processo, deformações de vários tipos introduzindo
assim erros de medição, na forma de retroação.
Assim, é necessário manter-se a força de medição em valores mínimos necessários ao
funcionamento dos SM e, adicionalmente, mantê-la constante ao máximo possível para se poder
levar, eventualmente, em consideração nas correções.
A força de medição está, por exemplo, no caso de um micrômetro externo, na faixa entre 5 a 10
N. No relógio comparador comum usa-se a força de medição entre 0,8 até 1,5 N, com variação
14

20. da mesma de 0,4 N no máximo; no caso de alguns relógios comparadores, a força de medição é
de 3 até 6 N, ou por outro lado, apenas 0,15 a 0,40 N. Interessante é que deixando-se descer a
haste do relógio comparador bruscamente de um altura de 20 mm apenas, ocorre um ‘pico’ de
força de medição dinâmica de até 70 N apesar da força estática ser de somente algumas
unidades de N.
b) Deformações
Deformações que ocorrem na medição não devem ser, sob hipótese alguma, de caráter
permanente, mas sim, exclusivamente, elásticas. Deste ponto de vista há certo perigo nas áreas
de contato entre o sensor (especialmente o de forma arredondada) e o objeto quando ocorrer um
choque dinâmico.
Deformações indesejáveis podem ocorrer, também, pelo peso próprio, quer do sistema de
medição, quer do objeto a medir especialmente se for usado apoio inadequado para os mesmos.
As inevitáveis deformações ou são mantidas dentro de determinados limites através de
dimensionamento adequado da peça, ou são isoladas e convenientemente consideradas
(correções introduzidas) no resultado da medição. Os limites admissíveis das deformações
dependem das correspondentes exigências quanto a incerteza de medição máxima permitida para
o processo.
As deformações podem ter caráter de variação de comprimento (encurtamento ou alongamento),
de flexão, de distorção ou de achatamento na região de contato.
b.1) Variação de comprimento:
A variação elástica de comprimento L em (mm) calcula-se com base na lei de Hooke:
F .L
∆L =
E. A
onde:
F (N): Força atuante
L (mm): Comprimento sujeito a variação
E (N/mm2): Módulo de elasticidade
A (mm2): Área da seção transversal
Exemplo numérico: Uma régua de E = 21,5. 104 N/mm2, de aço com dimensões 9 x 35 mm,
A = 315 mm2, L = 1000 mm, sendo carregada axialmente por uma força de medição de 10 N,
sofrerá encurtamento,
∆L =(10).(1000)/(315).(21,5.104 ) = 0,000147 mm = 0,15 µm
15

21. b.2) Flexão:
As deformações transversais de elementos dos sistemas de medição ou objetos, podem ser
calculadas em casos simples usando-se as fórmulas para vigas sobre dois apoios ou engastadas.
A flecha máxima y (µm) de um mandril cilíndrico apoiado pelas extremidades, entre pontas de
medição, calcular-se-á pela fórmula:
P.L3
Y = 425 ⋅
E.d 4
onde P (N) é a força de medição atuando na metade do comprimento L (mm) entre apoios, e d
(mm) é o diâmetro do mandril.
A flecha devido ao peso próprio do mesmo mandril de aço com módulo de elasticidade
(E = 21,5 . 104 N/mm2, e densidade = 0,078 (N/cm 3) calcula-se pela fórmula:
L4
Y = 7,6 ⋅ 2 ⋅ 10 −8
d
Para se ter uma idéia sobre valores absolutos observar-se-ão alguns exemplos numéricos:
• O mandril de aço, de comprimento L = 500 mm, de diâmetro d = 30 mm flete, por peso
próprio no meio em 5 µm. O mesmo mandril, sob força de medição de 1 N flete no meio em
0,3 µm.
• Um suporte de relógio comparador, de aço, cuja parte vertical tem o comprimento L = 200
mm e a parte horizontal em balanço de comprimento a = 70 mm, sendo a seção transversal
das duas partes circular, de diâmetro d = 20 mm, recua verticalmente, na sua extremidade
em balanço, sob força de medição de 1 N, em 0,6 um.
Em alguns casos, por escolha adequada dos pontos de apoio, pode-se obter deflexões mais
convenientes.
Por exemplo, um bloco padrão longo, apoiado em dois cutelos colocados a uma distância das
extremidades de a = 0,2113 . L (figura 1.20a) (onde L é o comprimento total do bloco) manterá
ambos os planos extremos (superfícies de medição) paralelos apesar da deflexão transversal. A
mesma distância entre apoios é recomendável para escalas, com divisões na parte superior da
régua.
Para as escalas, cujas divisões são gravados na linha neutra da seção transversal, o apoio em
"pontos de Bessel", na distância de a = 0,22031 L, proporciona o encurtamento mínimo do
comprimento total L (figura 1.20b).
16

22. Fig. 1.20 – Deformações devido ao peso próprio.
No caso de uma régua ser usada em seu comprimento total, recomenda-se que os pontos de
apoio estejam ajustados de a = 0,22315.L dos extremos. Neste caso, obtém-se a deflexão
transversal mínima, sendo a deformação nos extremos igual à flecha no meio da régua (figura
1.20c).
Se a régua for usada apenas na sua parte central entre os apoios, é vantajoso colocar os cutelos
de apoio na distância de a = 0,2386.L das extremidades. Neste caso a deformação transversal
na região entre os apoios será pequena, sendo igual a zero na metade da distância (figura
1.20d).
b.3) Achatamento:
Por achatamento se entende a aproximação que ocorre ente o sensor do sistema de medição e a
peça após o primeiro contato físico, em função da ação de uma força de medição. Pode ser
calculado, para os casos simples de contato, pelas equações de Hertz, porém, com coeficientes
estabelecidos experimentalmente.
Nas fórmulas que seguem, tem-se:
a (µm) = valor do achatamento;
F (N) = força de medição que aperta uma superfície contra a outra
d (mm) = diâmetro da esfera ou do cilindro;
L (mm) = comprimento de contato (se aplicável).
17

23. As fórmulas que seguem são válidas para peças e sensores de aço:
- Duas esferas iguais, ou cilíndricos cruzados
F2
a = 0,52575 ⋅ 3
d
- Esfera sobre um plano
F2
a = 0, 4173 ⋅ 3
d
- Cilindro sobre um plano
F 3 L
a = 0,047 ⋅ ⋅
L d
Para ilustração, um apalpador semi esférico atuando sobre um bloco padrão provoca um
achatamento a = 0,5 µm, se F = 3 N e d = 5 mm.
c) Desgaste:
O desgaste ocorre nas superfícies de medição de um instrumento sempre quando há um
movimento relativo entre as superfícies em contato e, portanto, quando se tem atrito.
Deve-se pois, dentro do possível, evitar o movimento da superfície de medição sobre a peça e/ou
reduzir o atrito.
Em muitos casos, entretanto, tem-se de contar para as superfícies em contato dos instrumentos de
medição, materiais de alta resistência ao desgaste: aços de ferramentas com liga especial,
camadas de cromo duro, minerais (por exemplo: ágata).
Não só as superfícies de medição estão sujeitas ao desgaste, mas todas as superfícies móveis de
um SM, nas quais ocorre atrito.
Recomenda-se então, já por ocasião do projeto, providenciar elementos e/ou mecanismos que
possibilitem ajustagem e, consequentemente, eliminação adicional do desgaste.
O usuário por sua vez deve inspecionar os sistemas de medição periodicamente e, se necessário,
fazer a reajustagem. O problema é que em virtude da interação de diversos fatores, o desgaste
não decorre nas superfícies uniformemente: superfícies planas tornam-se côncavas ou convexas,
guias apresentam folgas maiores apenas em certos lugares, e semelhantemente. A eliminação
completa do desgaste ocorrido torna-se, pois, muito difícil e as superfícies desgastadas dão
origem a erros de medição.
18

24. 1.4.2 Fatores de Natureza Geométrica
a) Forma geométrica da peça a medir:
Uma peça mecânica é representada, num desenho técnico, sempre em sua forma ideal e com
dimensões nominais. A peça depois de executada, não só diverge deste ideal em suas dimensões
mas, também, em sua forma geométrica.
De acordo com a técnica utilizada na fabricação a superfície apresenta diferentes rugosidades,
asperezas, etc., que são chamadas de erros microgeométricos.
Os desvios da forma geométrica geral (retilineidade, cilindricidade, planeza de superfícies) são
denominados erros da macrogeometria.
Os desvios macrogeométricos afetam o processo de medição e por isso as relações geométricas
de posição entre o sistema de medição e peça devem ser conhecidas, com clareza, para evitar
erros de medida.
Isto exige que se meça de tal modo que os desvios macrogeométricos possam ser identificados.
Assim, tendo-se, por exemplo, uma placa retangular fabricada - erroneamente - em forma de um
quadrilátero (figura 1.21a) e tomando-se a medida em dois sentidos perpendiculares, em dois
lugares a e b, apenas, obtém-se, por exemplo, para a medida a um valor completamente
deliberado (que dependerá do lugar da medida, a1, a2, a3, etc.) e o operador não perceberá o
desvio da forma. Para identificar os erros de forma geométrica da peça é necessário medi-la em
vários lugares, (por exemplo, a1, a2, b1, b2 na figura 1.21b).
a2
b
b1
a3
a2 b2
a1
a1
Fig. 1.21 – Erros macrogeométricos em peças.
Peças cilíndricas, eixos ou pinos, podem afastar-se da forma circular em vários pontos de sua
secção transversal, além disso, afastar-se da forma cilíndrica reta em vários pontos na direção
axial. A figura 1.22 apresenta alguns exemplos esquemáticos.
19

25. Fig. 1.22 – Erros macrogeométricos em peças cilíndricas.
Se em lugar da forma circular exata ocorre uma forma oval (figura 1.23a) então pode-se
determinar o diâmetro máximo e mínimo da mesma com duas superfícies de medição paralelos,
a, b, por exemplo, num paquímetro, micrômetro, etc, obtendo-se a diferença A ("ovalidade").
Usando-se, neste caso, um prisma (figura 1.23b) como apoio para a medição com um relógio
comparador R, a diferença B entre os diâmetros apresenta-se apenas em proporção reduzida
(sendo B < A).
a) b)
B<A
A
a
b
prisma
Fig. 1.23 – Erros geométricos de circularidade – ovalidade.
Se ocorrer, por outro lado, um iso-espesso E, figura 1.24, a medição entre planos paralelos não
registrará o erro de circularidade. O registro da excentricidade faz-se com auxílio de prisma. O
melhor resultado oferece o prisma cujo ângulo é relacionado com o número n de lados do iso-
espesso de acordo com a fórmula.
20

26. 360°
α = 180° − k ⋅
n
onde k são os números inteiros 1, 2, 3, ... , assim, obtém-se a seguinte tabela:
NÚMERO DE LADOS ÂNGULO DO
DO IS0-ESPESSO PRISMA EM (º )
3 60
5 108 ou 36
7 128,6 ou 77,1
9 140 ou 100 ou 160
Fig. 1.24 – Erros macrogeométricos de circularidade – iso-espesso.
Quando se suspeita da presença de algum desvio da forma circular, porém, não se sabe se se
trata do oval (ou alguma forma do mesmo com o número par dos lados) ou de iso-espesso (cujo
número de lados é desconhecido), a medição procede-se entre dois planos paralelos e depois
pelo menos em dois prismas diferentes, de ângulos 60o e 90o, respectivamente. O ângulo de 90o,
apesar de que não constar na tabela acima, é suficientemente perto dos valores 108o ou 77,1o
citados.
Os problemas da influência da forma geométrica estão intimamente relacionados com as
dimensões das medidas e das tolerâncias. Para a técnica de medição de comprimentos, deve
ficar claro que, para a determinação da configuração real de uma peça, jamais basta uma única
medida, mas que sempre é necessário considerar várias medidas, bem como a relação entre as
mesmas.
21

27. b) Erro de Contato
Os elementos do instrumento de medição que tocam a peça a medir, ou seja, os sensores de
medição, devem ter a forma correspondente a configuração da peça, a fim de que se obtenha o
contato geometricamente bem definido: se a peça a medir é plana, o sensor de medição é
geralmente esférico, figura 1.25a. Se por outro lado, a peça é esférica ou cilíndrica, usam-se
sensores planos de medição, figura 1.25b. Na medição de roscas utilizam-se pontas sensoras de
forma cônica, cilíndrica ou esférica.
Se o contato entre a peça a medir e a superfície de medição, devido a erros de forma de uma ou
de outra não tem uma relação geométrica exata, correspondente ao recobrimento geométrico
desejado, acontece então o que denominamos de erro do contato.
a) b) peça c)
peça
β
B
peça A
Erro de contato
Fig. 1.25 – Contato entre sensor do sistema de medição e a peça a medir.
Na figura 1.25c tem-se o erro de contato em sua forma mais simples, quando não há
recobrimento geométrico entre a superfície plana da peça A e a superfície plana de medição B de
modo que as duas tocam uma a outra em ângulo (fortemente exagerado no desenho). Este é um
exemplo típico de situação que acontece, por exemplo, quando medimos uma peça com um
micrômetro ou uma máquina de medir em que os sensores de medição apresentam erros de
paralelismo acentuado, gerando efetivamente erros de medição significativos.
A maioria dos problemas com erro de contato elimina-se por uma forma geométrica impecável
das superfícies de medição.
c) Relações Geométricas de Posição:
Erros geométricos de posição de medição são evitados, de forma mais segura pelo emprego do
método da substituição. A dimensão da peça é captada com auxilio de um dispositivo e depois
comparado a padrões de medição colocados exatamente no lugar e na posição da peça. Assim,
não podem ocorrer erros de posição devidos a movimentação de cursores (não perfeição de
guias) ou problemas semelhantes.
Se o método da substituição não puder ser aplicado, deve-se ao menos obedecer ao princípio de
ABBE, enunciado por Ernst Abbé, que exige que “o trecho a medir deve constituir o
prolongamento retilíneo da escala que serve como dispositivo de medição”. Ambos, trecho a
22

28. medir, bem como o padrão de medida, devem ser dispostos no mesmo eixo um atrás do outro.
No esquema de um paquímetro na figura 1.26, observa-se, que o princípio de Abbé não é
respeitado na configuração do instrumento o que implica na menor confiabilidade dos resultados:
o trecho a medir "dA" (diâmetro de uma peça) encontra-se paralelo a escala de medição.
Observa-se que no instante da medição ocorre um erro em função da distância S entre a escala
do instrumento e o ponto de contato entre os sensores de medição e a peça. Nestes casos deve-
se realizar as medições posicionando-se a peça a medir o mais próximo possível da escala do
instrumento de medição, de modo a diminuir a distância S, e portanto, reduzir o erro de medição.
dA
φ Erro de 1a ordem
S
EI = S * tan φ
EI
Fig. 1.26 – Erro de primeira ordem – disposição paralela do padrão com a peça.
Já no caso de um micrômetro (figura 1.27) o trecho a medir “L” situa-se no prolongamento
retilíneo da escala de medição que, neste caso, fica realizada pelo parafuso de medição do
micrômetro. Respeitado o princípio de Abbé, obtém-se resultados com substancial minimização
de erros, já que ocorrem somente os de 2o ordem.
23

29. L’ L
θ cos θ =
L'
L
ERRO DE 2O ORDEM
L ⋅θ 2
0 – 25 mm 0.01mm E=
2
Fig. 1.27 – Erro de segunda ordem – disposição alinhada do padrão com a peça.
1.4.3 Fator de Natureza Física
Deformação térmica:
Como o volume dos materiais metálicos sofre alteração com a variação da temperatura, é
extremamente importante estabelecer uma temperatura de referência.
A temperatura de 20,0 oC é hoje adotada internacionalmente como temperatura de referência
para apresentação de resultados de medição ou calibração de instrumentos de medição da Área
de Metrologia Dimensional. Assim, os resultados do comprimento de blocos padrão, os
resultados da calibração de uma Máquina de Medir por Coordenadas, entre outros, são válidos
para a temperatura de 20,0 oC.
Nas medições de comprimento é necessário dar uma atenção toda especial à temperatura em
virtude da deformação térmica sofrida pelos instrumentos, padrões, alguns dispositivos utilizados
no processo de medição, além das deformações sofridas pelas próprias peças sujeitas a medição.
A variação de comprimento é calculada pela fórmula:
∆L = L ⋅ ∆t ⋅ α
onde: ∆L - Variação de comprimento (encurtamento ou alongamento do comprimento L);
L - comprimento original;
α - coeficiente de expansão térmica;
∆t - a diferença de temperaturas.
24

30. Exemplo: Um bloco prismático de aço de comprimento de 1 metro a 20,0 oC, terá na
temperatura ambiente de 26,0 oC o comprimento de 1000,069 mm, já que
L+∆I = I000 + 1000 . 11,5 . 10-6 . 6 = 1000,069 mm
Para o aço, o coeficiente α = 11,5 µm/m.K
Se a peça a medir tem o mesmo coeficiente de expansão térmica do padrão usado (escala, bloco
padrão, etc.), com o qual será comparado, não ocorrerá erro de medição por razões térmicas,
mesmo quando a medição se efetua em temperatura diferente da de referência (20,0 oC) já que o
padrão se deforma na mesma proporção que a peça a medir. Evidentemente isto só ocorrerá se
ambos, peça e padrão/instrumento estiverem na mesma temperatura (o que pode ser obtido
deixando-se peça e padrão/instrumento estabilizando termicamente por um período de tempo
suficiente para atingir-se o equilíbrio térmico). Este é o motivo pelo qual os metais leves só podem
ser usados em instrumentos de medição mediante cuidados especiais a não ser no caso particular
em que as próprias peças são de metal leve. Por razões semelhantes não se utilizam calibradores
e padrões de vidro, apesar de serem mais baratos e bastante resistentes ao desgaste.
Se a peça tiver um coeficiente de expansão térmica distinto do padrão (o que às vezes é
inevitável), como por exemplo, padrão de aço e peça de latão, então ocorrerá um erro quando a
temperatura de medição diferir da temperatura de referência de 20,0 oC. Se, além disso houver
ainda diferença de temperatura entre peça e padrão (instrumento de medição utilizado no
processo de medição), podem ocorrer erros ponderáveis de medição devidos a efeitos térmicos.
Se as temperaturas do padrão e da peça a medir diferirem de 20 oC em ∆t1 e ∆t2 e se os
coeficientes de expansão térmica forem α 1 e α 2, respectivamente, o erro de medição ∆L para um
comprimento L será:
∆L = L ⋅ ( ∆t 1 ⋅ α1 − ∆t 2 ⋅ α2 )
Do anterior exposto, conclui-se uma aplicação importante para a prática de medição. Deve-se
assegurar que a temperatura da peça e do sistema de medição sejam próximas tanto quanto
possível da temperatura de referência. Isto se obtém deixando ambos durante certo tempo num
ambiente a 20 oC. O tempo necessário para a equalização da temperatura depende do porte e
tipo de cada um dos elementos, e da diferença inicial de temperaturas, variando para as peças
usuais entre 4 e 24 horas. Favoravelmente influi se ambos elementos repousam sobre a mesma
base metálica.
Se o tempo para equalização de temperaturas foi insuficiente corre-se o risco de que diversas
partes da peça ou do padrão apresentem diferenças de temperaturas entre si, o que provocará
não só erros em dimensões, mas também erros de forma. Semelhantemente, deve-se impedir que
ocorram variações de temperatura durante a própria medição.
O quadro apresentado a seguir sintetiza as diversas possibilidades de combinações entre
25

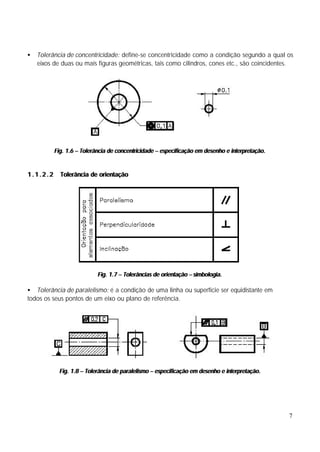
31. materiais e temperatura:
PEÇA SM
CASO ERRO
MATERIAL TEMPERATURA MATERIAL TEMPERATURA
1 A 20 OC A 20 OC -
2 A T ≠ 20 C
O
A T -
3 A T A t≠T α A(T-t)L
O O
4 A 20 C B 20 C -
5 A T ≠ 20 C
O
B T [α A(T-20) - α B(T-20)]L
6 A T B t≠T [α A(T-20) - α B(t-20)]L
Onde: α A = coeficiente de dilatação térmica do material A (µm/m.K)
α B = coeficiente de dilatação térmica do material B (µm/m.K)
L = comprimento medido (m)
O erro é determinado em µm.
26

32. Capítulo 2
BLOCOS PADRÃO
2.1 GENERALIDADES
2.1.1 Definição
Blocos padrão são padrões de comprimento ou ângulo, corporificados através de
duas faces específicas de um bloco, ditas “faces de medição”, sendo que estas faces
apresentam uma planicidade que tem a propriedades de se aderir à outra superfície de
mesma qualidade, por atração molecular.
A característica marcante destes padrões está associada aos pequenos erros de
comprimento, em geral de décimos ou até centésimos de micrometros ( µm ), que são
obtidos no processo de fabricação dos mesmos. Em função disto, pode-se afirmar que os
Blocos Padrão exercem papel importante como padrões de comprimento em todos os
nível da Metrologia Dimensional.
2.1.2 Tipos
Quanto à forma da seção transversal do bloco, esta pode ser quadrada, retangular
ou circular (figura 2.1). Os blocos de secção quadrada ou circular podem ou não ser
furados no centro.
As dimensões dos blocos de secção quadrada são normalizados pela norma GGG-
G-15, norma americana. A grande vantagem destes blocos é a estabilidade
proporcionada pela forma da secção quando o mesmo é utilizada na posição vertical.
No brasil praticamente não se utilizam este tipo de bloco.
As dimensões dos blocos de secção retangular são normalizadas pela norma ISO
3650 e outras. Os blocos maiores de 100 mm apresentam furos em cada extremidade,
cuja finalidade é permitir a montagem de um dispositivo que garanta a união de uma
composição formada por dois ou mais blocos.
2.1.3 Fabricação
a) Material
Os blocos padrão são fabricados em aço liga, metal duro, cerâmica, entre outros. Para
os blocos em aço, quando for exigida uma alta resistência ao desgaste, as superfícies de
medição podem ser protegidas por dois blocos protetores, fabricados de metal duro
( carbonetos sinterizados).
Como o aço tem tendência de alterar o seu volume com o decorrer do tempo, a
estabilidade dimensional dos blocos padrão pode ser significativamente afetada. Para
minimizar este fenômeno usa-se liga que tenha uma boa estabilidade dimensional.
1

33. Na figura 2.2 é apresentado o resultado de calibração de blocos padrão entre 1970 e
1991, realizados no PTB, órgão primário em metrologia na Alemanha. Os blocos padrão
calibrados, de comprimento 24,5 , 30 , 80 e 100 mm, nunca foram utilizados em
processos de medição. Observa-se que dois blocos, o de 100 e 30 mm, apresentavam
comprimento de valor próximo a 0,5 µm durante este período. Observa-se também que
esta alteração ocorreu distintamente para cada bloco. Os blocos de 100 e 80 mm
tiveram alteração de comprimento positiva e os de 30 e 24,5 mm tiveram alteração de
comprimento negativa, isto é, reduziram seus comprimentos. Um bloco seria considerado
estável caso seu comportamento fosse próximo daquele do exemplo da figura 2.1, isto é,
as variações de comprimento são insignificantes e oscilam em torna da linha zero.
As variações de comprimento permitidas para cada bloco a cada ano, são em geral
especificadas nas normas técnicas, como por exemplo a norma DIN 861.
Os fabricantes de Bloco Padrão em cerâmicas a base de zircônio afirmam que este
efeito é significativamente menor nestes blocos, como veremos adiante.
É importante que se tenha conhecimento do coeficiente de expansão térmica do
material e do módulo de elasticidade a fim de que, quando usado em medições
criteriosas, os correspondentes erros possam ser compensados.
b) Processo
Para os blocos de aço até cerca de 100 mm de comprimento, eles são inteiramente
temperados. Nos comprimentos maiores apenas os extremos são endurecidos.
Para realizar o alívio de tensões, aplicam-se diversos processos de “envelhecimento
artificial” de acordo com a composição química do aço utilizado.
O elevado grau de acabamento das superfícies de medição é obtido através de
lapidação fina, que assegura grau de planicidade e ao mesmo tempo, uma rugosidade
baixíssima das mesmas.
2.1.4 Normas e Fabricantes
Relaciona-se a seguir algumas normas e recomendações técnicas referentes a
definição, tipos e uso de blocos padrão.
Alemã : DIN 861, DIN 2260
VDE/VDI 2605 (Blocos Padrão angulares)
Francesa : NF E 11-010
Inglesa : BS 4311 (Blocos Padrão de seção retangular)
BS 5317 (Blocos Padrão de seção circular, “barras”) e
NPL SPECIFICATION MOY/SCMI/1B (Blocos Padrão angulares).
Suíça : VSM 57100
Japonesa : JIS B 7506
2

34. Americana : GGG-G-15
Internacional : ISO 3650
Como principais fabricantes no mundo citam-se: CARL ZEISS, KOBA, MITUTOYO,
KURODA, MATRIX, STARRETT-WEBBER, CEJ, MAHR, TESA, etc.
Figura 2.1: Tipos de Blocos Padrão (BP).
Figura 2.2: Alteração do Comprimento de Blocos Padrão.
3

35. 2.1.5 Apresentação – Jogos
A fim de alcançar um bom aproveitamento dos blocos padrão, estes são reunidos em
jogos que se diferem entre si pelos seguintes fatores: mínimo escalonamento, faixa que o
escalonamento abrange número de peças que os constituem.
Estes jogos consistem de várias séries dimensionais ( sub-grupos de dimensões).
Partindo de base 1,000 mm, existem séries dimensionais em milésimos de mm (1,001 até
1,009), centésimos (1,01 até 1,09), décimos, etc. Os jogos mais usuais são padronizados
pela DIN 2260. Um jogo de blocos padrão bastante usado é o chamado jogo normal,
denominado jogo “N”. Compõe-se de 45 peças que formam 5 séries
dimensionais conforme consta na figura 2.3. O jogo permite compor qualquer dimensão
entre 3 103 mm com escalonamento de 0,001 mm.
Fora dos limites mencionados, o jogo permite a realização de algumas medidas
(porém, não todas) com o escalonamento indicado. Não se pode compor, por exemplo,
as medidas 1,011, ..., 1,019. Outra limitação é que para a composição de medidas fora
dos limites é necessário juntar maior número de blocos padrão, do que o previsto pela
norma, o que resulta na introdução de maiores erros.
2.2 ASPECTOS OPERACIONAIS
2.2.1 Recomendações de Utilização
Enorme cuidado é tomado pelo fabricante de um jogo de blocos padrão: na seleção
do material, na retificação, no tratamento térmico, nos processos de lapidação, na
inspeção, na gravação das inscrições e números, na calibração e na embalagem dos
mesmos.
Mesmo os Blocos Padrão de grau 2 (DIN 861), usados nas oficinas, devem ser
manuseados por pessoal experiente a fim de que em pouco tempo os blocos não estejam
desgastados. Alem disto, o operador deve:
- Evitar o aparecimento de oxidações nas superfícies de medição resultante de
umidade, agentes corrosivos, etc. Para isto é necessário que após cada dia de
trabalho os blocos sejam limpos com benzina ou similar e untados com uma camada
de vaselina. Este material de limpeza deve ser de preferência de uso exclusivo dos
blocos padrão.
- Usar pinças de madeira ou plástico para manipular blocos pequenos.
- Evitar usar os blocos em superfícies oxidadas, ásperas ou sujas.
- Evitar a todo custo um coque mecânico (queda, batida com outro sólido). Mas
ocorrendo, deve-se examinar ambas as faces de medição, usando um plano ótico, a
4

36. fim de verificar se há amassamentos (deformações permanentes) que prejudicarão a
aderência e a própria planicidade de outros colocados em contato.
- Evitar a atuação de radiação térmica, campos magnéticos e elétricos.
- Manter em suas respectivos embalagens quando não usados.
- Evitar de deixar os blocos padrão aderidos por muito tempo.
Todas as recomendações citadas devem ser mais rigorosas quanto melhor for a
classe de erro do Bloco Padrão.
2.2.2 Composição de Blocos Padrão
É muito comum na indústria, ser necessário a utilização de comprimento padrão não
disponíveis diretamente através de um bloco, sendo necessário a combinação de duas ou
mais peças.
As superfícies de medição de blocos padrão (em função de sua elevada planicidade e
acabamento superficial) aderem uma à outra (“colam-se”) quando se ajustam
progressivamente entre si, através do deslizamento e leve pressão. Para obter esta
aderência é indispensável (além do bom estado das superfícies sem riscos, batidos,
amassamentos, etc, mesmo que mínimos) que não fiquem quaisquer partículas estranhas
( pós, por exemplo), entre as superfícies em questão. Recomenda-se o seguinte
procedimento: as superfícies devem ser primeiramente limpas com benzina retificada ou
similar, eliminando-se graxa velha oxidada e pó. Aplica-se, em seguida, uma quantidade
mínima de vaselina pura, especial, que espalha-se com pano limpo. Procedendo desta
maneira, a superfície do bloco padrão fica limpa (brilhante) sendo coberta apenas por
um filme mínimo (invisível) de vaselina. Uma vez preparadas as superfícies
correspondentes de dois blocos a serem aderidos, os mesmos são justapostos com os
eixos maiores de seção transversal inicialmente perpendiculares entre si, de acordo como
é apresentado na figura 2.4a , usando-se um certo movimento relativo deslizante no
sentido da flecha. Por giro e leve pressão (figura 2.4b) ambas as superfícies são levadas a
uma superposição completa (figura 2.4c) ligando-se entre si por adesão entre as
moléculas dos dois blocos e ficando “aderidas” (coladas).
2.2.3 Acessórios
Os blocos, principalmente os de trabalho, nem sempre são usados isoladamente.
Em conjunto com outros acessórios podem ter diversas funções (figura 2.5).
- Base: é útil quando se utilizar blocos grandes sem que haja o perigo de tombarem.
Junto com outros acessórios pode formas um graminho de precisão.
- Porta blocos: serve para manter vários blocos aderidos em conjunto com blocos de
transferência.
- Blocos de transferência: há vários tipos que junto com o porta blocos cria uma gama
de instrumentos: graminho, calibrador de roscas internas, etc.
5

37. - Blocos protetores: são Blocos Padrão de metal duro aderidos à superfícies extremas
de blocos padrão comuns, quando estes estiverem sendo usados em meio hostil, isto
é, provocando desgaste.
Conjunto Especial Conjunto Standard ( Normal )
Série Blocos Escalonamento Série Blocos Escalonamento
dimensional número dimensões dimensional número dimensões
1 9 1,001 até 1,009 0,001 1 9 1,001 até 1,009 0,001
2 49 1,01 até 1,49 0,01 2 9 1,01 até 1,09 0,01
3 19 0,5 até 9,5 0,5 3 9 1,1 até 1,9 0,1
4 9 10 até 90 10 4 9 1 até 9 1
5 9 10 até 90 10
Conjunto Conjunto Conjunto Standard
Standard Especial ( 2ª combinação )
1,005 1,002
1,08 1,005 1,003
1,9 1,48 1,03
3 4,5 1,05
90 90 1,1
96,985 96,985 1,8
40
50
96,985
Dimensões Comprimento a b
dos blocos Medida Tolerância Medida Tolerância
b de 0,5 até 10,1 30
b +0 9 -0,05
de 10,1 até 1000 35 -0,3 -0,2
a
Figura 2.3: Padronização de BP.
Figura 2.4: Colagem de Blocos Padrão.
6

38. 2.3 DEFINIÇÃO DE COMPRIMENTO DE UM BLOCO PADRÃO E ERROS
2.3.1 Comprimento de um Bloco Padrão
“O comprimento de um bloco padrão de superfícies plano-paralelas é igual ao
afastamento entre duas superfícies planas de medição das quais uma é a superfície de
um corpo auxiliar na qual o bloco padrão está inteiramente ligado por uma das suas
faces e a outra é a face livre do bloco padrão”. As premissas são:
- o bloco padrão não está solicitado mecanicamente de maneira alguma que poderia
provocar variação de comprimento;
- o corpo auxiliar é do mesmo material e com a qualidade (e textura) da superfície
igual às do bloco padrão;
- a ligação entre o bloco padrão e o corpo auxiliar é feita da mesma maneira como
descrito para ligação de blocos padrão entre si, sendo excluídos expressamente
quaisquer meios que poderiam favorecer a adesão.
Por outro lado, conta-se com um filme “infinitesimal” de lubrificante entre as
superfícies de medição, como ocorre no uso normal de blocos padrão justapostos.
Os blocos padrão são executados e medidos quanto ao comprimento que
corporificam, bem como quanto a sua forma geométrica: planicidade, paralelismo e o
grau de acabamento das suas superfícies de medição.
2.3.2 Caracterização dos Erros
Os parâmetros mais importantes que caracterizam metrologicamente os blocos padrão
são o erro do meio e a constância de afastamento (paralelismo e planicidade
associadas).
a) Erro do meio (Em)
O erro do meio é a diferença entre o comprimento efetivo do bloco padrão na região
central (Lm), e o comprimento nominal (Ln), (figura 2.6).
Em = Lm – Ln
b) Constância de Afastamento (CA)
É a combinação dos erros de paralelismo e planicidade, e corresponde a diferença
entre o maior e o menor comprimento entre as faces do bloco padrão, quando medido
nos quatro cantos e no centro. É caracterizada na figura 2.6 como sendo a soma do
desvio positivo (D.pos. = comprimento máximo menos o comprimento do meio) com
desvio negativo (D.neg. = comprimento do meio menos o comprimento mínimo).
Assim:
CA = Lmax - Lmin
7

39. Figura 2.5: Acessórios de Blocos Padrão.
Figura 2.6: Erros de Blocos Padrão.
8

40. 2.4 AS CLASSES DE ERRO E SUAS APLICAÇÕES
Pela norma DIN 861 e ISO 3650 os blocos são classificados quanto ao erro do meio e
constância de afastamento em cinco classes de erro, a saber: 00, K, 0, 1 e 2. O máximo
erro admitido em cada uma das classes (tolerância de fabricação) é dado em função do
comprimento, conforme pode ser observado na tabela figura 2.7.
A seleção da classe de erro depende da finalidade para a qual o bloco padrão se
destina.
Pode-se adotar as seguintes recomendações:
- Classe de erro 00 – especialmente indicada como padrão de referência em
laboratórios de Secundários de Metrologia (laboratórios credenciados na RBC, por
exemplo). É usada na calibração de blocos padrão com classe de erro 0, 1 e 2 pelo
método diferencial de medição (método de comparação).
- Classe de erro K – apresenta a mesma tolerância de constância de afastamento da
classe “00”, porém tolerâncias no comprimento (Em) iguais ao da classe 1. A
principal vantagem em ralação a classe ”00” é o custo mais baixo com a mesma
qualidade metrológica, já que os erros do meio (Em) são corrigidos durante a sua
utilização.
- Classe de erro 0 – para altas exigências, em medições criteriosas no ajuste de
máquinas de medição, em medições diferenciais criteriosas durante a qualificação
de padrões e calibradores quando se exige pequena incerteza de medição. É a
classe de erro utilizada como referência para calibração de blocos da classe 1 e 2.
O uso é restrito, quase que exclusivamente para laboratórios de metrologia
dimensional.
- Classe de erro 1 – usa-se para as mesmas finalidades acima, porém, onde as
tolerâncias não são tão rígidas, por exemplo, no posto central de controle de
qualidade da fábrica.
- Classe de erro 2 – para uso geral, ajuste de instrumentos convencionais, medições
diferenciais onde o nível de tolerância não é apertado.
Quanto a sua aplicação (não quanto à classe de erro) os blocos padrão classificam-
se em:
- blocos padrão de trabalho
- blocos de verificação
- blocos de comparação
- blocos de referência
Em geral, a classe superior (exemplo, referência) serve como padrão para calibrar e
controlar classes imediatamente inferior (exemplo, comparação).
9

41. Os blocos padrão de trabalho, já que são usados no nível de oficina, entram em
contato com superfícies relativamente ásperas, e sofrem por isso uma forte solicitação de
desgaste. É indispensável uma calibração dos blocos padrão em intervalos de tempos
definidos, dependendo da intensidade de uso.
Os blocos de referência, por outro lado, devido ao pouco freqüente, limitado aos
casos de grande importância (calibração) sofrem desgaste mínimo e conservam suas
características metrológicas por períodos prolongados de tempo.
Em laboratórios de metrologia é imprescindível a existência de padrões de referência,
que são blocos padrão com certificados de calibração nos quais são indicados os erros
do meio e constância ser recalibrados.
2.5 ERRO DE UMA COMPOSIÇÃO DE BLOCOS
O erro ∆L de uma composição de blocos padrão calcula-se a partir dos erros do
meio (Em) dos blocos padrão que formam a composição do comprimento em questão.
Como exemplo, analisar-se-á o erro da composição os comprimento de 138,345 mm,
composta dos blocos padrão de classe de erro 1, de acordo com a primeira coluna da
tabela 2.1.
COLUNA 1 COLUNA 2 COLUNA 3 COLUNA 4 COLUNA 5 COLUNA 6
Comprimento Erros Erros Quadrados dos 2/3 do erro Quadrados dos
dos blocos individualmente máximos erros máximos máximo valores da
padrão na medidos (dados permitidos permitidos permitido coluna 5
composição de calibração) (µm) (µm)
(mm) (µm)
1,005 + 0,20 ± 0,20 0,04 ± 0,133 0,018
1,04 - 0,18 ± 0,20 0,04 ± 0,133 0,018
1,3 - 0,15 ± 0,21 0,04 ± 0,140 0,020
5 - 0,20 ± 0,22 0,05 ± 0,147 0,022
40 + 0,32 ± 0,36 0,13 ± 0,240 0,058
90 + 0,48 ± 0,56 0,31 ± 0,373 0,140
138,345 + 0,47 ± 1,75 0,61 ± 1,166 0,276
Tabela 2.1 – Avaliação dos erros de um comprimento formado com blocos padrão classe
de erro 1.
Se o erro Em, em cada um dos blocos padrão usados na composição é realmente
conhecido (fixado, por exemplo, pela medição comparativa, ou seja, através de
calibração, com um jogo de blocos padrão da classe de erro K), o erro da composição é
obtido como uma soma algébrica simples dos erros individuais dos blocos. Os erros dos
blocos padrão, individualmente estabelecidos em uma operação de calibração,
encontram-se, junto com os sinais reais, na Segunda coluna da tabela, sendo o erro da
composição igual à soma algébrica dos mesmos, ou seja, DL = +0,47 mm.
10

42. Se os erros individuais não são conhecidos, utiliza-se para avaliação do erro da
composição os desvios admissíveis de cada bloco padrão, de acordo com a norma e a
sua classe de erro. Na terceira coluna da tabela, tem-se os erros admissíveis dos blocos
para classe de erro 1. A soma dos valores positivos (negativos) dá o valor máximo
positivo (negativo) do erro da composição. Este valor máximo poderia ocorrer quando na
composição todos os blocos tivessem o máximo erro permitido e, mais ainda, todos com
o mesmo sinal. Já que isto é muito pouco provável, O erro assim estabelecido não tem
sentido prático.
De acordo com a teoria de erros usa-se pois, a fórmula:
∆L = ± E M 1 ± E M 2 ± ... ± E Mn
2 2 2
onde:
EM1 ... EM2 são erros máximos permitidos. Os quadrados destes erros encontram-se na
quarta coluna da tabela, sendo a soma dos mesmos igual a 0,61. Ao se usar a fórmula
lembrada, obtém-se para o erro da composição:
∆L = ± 0,61 = ±0,78 = ±0,8µm
Como o procedimento que melhor corresponde à realidade, recomenda-se às vezes,
calcular o erro não com os desvios máximos como constam na terceira coluna da tabela,
mas com apenas 2/3 destes valores. Os valores respectivos podem ser apreciados na
quinta coluna da tabela e os quadrados dos mesmos na sexta coluna, resultando nas
somas 1,166 e 0,276 respectivamente. O erro da composição é pois,
∆L = ± 0,276 = ±0,53 = ±0,5µm
Para o cálculo informativo rápido pode-se usar a seguinte fórmula aproximada que
dispensa o cálculo moroso com quadrados e raiz quadrada.
∆L = ±  ... .∑ EM i
1 2 n
 
 2 3  i =1
Ao se substituir nesta fórmula as somas obtidas nas colunas terceira e quarta,
respectivamente, obtém-se, como erro da composição os valores
 1 2
∆L1 = ± ... .1,75 = ±(0,9até1, 2)µm
 2 3
∆L2 = ± ... .1,166 = ± (0,6até 0,8)µm
1 2
 
2 3
11

43. 2.6 BLOCOS PADRÃO DE CERÂMICA
Estes blocos padrão são fabricados com um tipo de cerâmica cujo componente base é
o ZIRCÔNIO, que é um dos materiais mais duráveis encontrados até hoje.
A seguir serão apresentadas as características mais importantes destes padrões, sempre
fazendo-se um paralelo com os blocos fabricados em aço e em metal duro.
Chama-se a atenção para o fato de que somente os resultados que serão descritos
adiante foram divulgados pelos fabricantes destes padrões. Somente o tempo poderá
confirmar integralmente as vantagens destes padrões em relação aos tradicionais blocos
padrão de aço.
2.6.1 Resistência a Corrosão
Os blocos padrão cerâmicos são totalmente imunes ao ataque de agentes corrosivos.
É uma grande vantagem, principalmente em função do contato constante destes padrões
com o suor humano. Em função disto, estes blocos dispensam tratamento anti-corrosivos
ou outros cuidados de armazenamento.
2.6.2 Resistência à Abrasão
E resistência à abrasão dos blocos cerâmicos é de cinco a dez vezes maior do que os
fabricados em aço e de quatro a cinco vezes maior de que os fabricados em metal duro.
Esta superioridade dos blocos cerâmicos é devido ao seu baixo coeficiente de atrito e
também à sua densa e homogênea estrutura granular.
Na figura 2.8 é apresentado o resultado da perda de material devido a abrasão para
blocos de diferentes materiais. Cada bloco foi carregado igualmente e friccionado com
movimentos circulares sobre um desempeno de ferro fundido (DIN-1693-77).
2.6.3 Estabilidade Dimensional
Diferente dos blocos fabricados em aço, os blocos não apresentam variação
dimensional significativa no decorrer do tempo. A figura 2.9a mostra comparativamente
as variações dimensionais de um bloco cerâmico de 100 mm (após a sinterização) e as
de um bloco de aço, também de 100 mm, após seu tratamento térmico.
2.6.4 Coeficiente de Expansão Térmica, Módulo de Elasticidade, Dureza e
Condutibilidade Térmica
Na figura 2.10 são apresentadas as principais propriedades físicas e mecânicas dos
blocos padrão de cerâmica, aço e metal duro.
Em função da proximidade entre os coeficientes de expansão térmica da cerâmica a
base de zircônio e o aço, os blocos padrão de cerâmica podem ser usados normalmente
12

44. como padrão de comprimento para medir peças em aço, o que constitui mais uma
vantagem para o uso destes últimos.
O fator de condutibilidade térmica da cerâmica é relativamente baixa comparada ao do
aço, o que significa dizer que o bloco cerâmico necessita o dobro do tempo,
comparativamente ao aço, para alcançar a temperatura ambiente (equilíbrio térmico). No
entanto, em algumas situações isto poderá se tornar tão rapidamente devido as
mudanças da temperatura ambiente, comparada ao sue similar de aço.
O tempo necessário para a estabilização térmica dos blocos de cerâmica depende das
condições ambientais, do comprimento do bloco, bem como da diferença inicial de
temperatura entre o bloco e o ambiente. Na figura 2.9b é apresentado o resultado da
estabilização térmica de dois blocos de 100 mm, um de aço e outro de cerâmica, que
foram segurados na mão durante três minutos e a seguir suas variações dimensionais
foram medidas.
Valores dos erros em µm
00 0 1 2 K
Comprimento
nominal
Em CA Em CA Em CA Em CA Em CA
mm
de até ± ± ± ± ±
-
- 10
10 0,06 0,05 0,12 0,10 0,20 0,16 0,45 0,30 0,20 0,05
10
10 25
25 0,07 0,05 0,14 0,10 0,30 0,16 0,60 0,30 0,30 0,05
25
25 50
50 0,10 0,06 0,20 0,10 0,40 0,18 0,80 0,30 0,40 0,06
50
50 75
75 0,12 0,06 0,25 0,12 0,50 0,18 1,00 0,35 0,50 0,06
75
75 100
100 0,14 0,07 0,30 0,12 0,60 0,20 1,20 0,35 0,60 0,07
100
100 150
150 0,20 0,08 0,40 0,14 0,80 0,20 1,60 0,40 0,80 0,08
150
150 200
200 0,25 0,09 0,50 0,16 1,00 0,25 2,00 0,40 1,00 0,09
200
200 250
250 0,30 0,10 0,60 0,16 1,20 0,25 2,40 0,45 1,20 0,10
250
250 300
300 0,35 0,10 0,70 0,18 1,40 0,25 2,80 0,50 1,40 0,10
300
300 400
400 0,45 0,12 0,90 0,20 1,80 0,30 3,60 0,50 1,80 0,12
400
400 500
500 0,50 0,14 1,10 0,25 2,20 0,35 4,40 0,60 2,20 0,14
500
500 600
600 0,60 0,16 1,30 0,25 2,60 0,40 5,00 0,70 2,60 0,16
600
600 700
700 0,70 0,18 1,50 0,30 3,00 0,45 6,00 0,70 3,00 0,18
700
700 800
800 0,80 0,20 1,70 0,30 3,40 0,50 6,50 0,80 3,40 0,20
800
800 900
900 0,90 0,20 1,90 0,35 3,80 0,50 7,50 0,90 3,80 0,20
900
900 1000
1000 1,00 0,25 2.00 0,40 4,20 0,60 8,00 1.00 4,20 0,25
Figura 2.7: Tolerâncias para Blocos Padrão segundo a norma DIN 861.
2.6.5 Aderência das Superfícies
Devido ao alto grau de uniformidade e densidade de sua estrutura granular, a
superfície dos blocos cerâmicos se auto aderem com a mesma facilidade dos blocos
padrão de aço em estado de novo. A força requerida para desmontagem de blocos
cerâmicos é aproximadamente 30% superior àquela necessária para desmontagem de
blocos de aço.
13

45. Figura 2.8: Blocos Padrão de Cerâmica: Resistência à abrasão.
Para ilustrar a eficiência das superfícies destes blocos , apresentamos a seguir os
resultados da composição dos comprimentos de 20 mm e 41 mm, através da montagem
de dois blocos, de 10 mm dois blocos de 20,5 mm, respectivamente.
Foram medidos os erros do meio de cada bloco utilizado. A soma dos erros de cada
par de blocos foram utilizados como referência para determinar o erro nominal da
composição.
Após montagem dos blocos (10 e 10mm / 20,5 e 20,5 mm), cada uma delas foi
também medida na posição central. O erro resultante da montagem foi calculado pela
diferença entre o erro do meio efetivo da montagem e a soma dos erros individuais de
cada bloco como apresentado na tabela 2.2.
Comprimento nominal dos blocos (mm) 10 10 20,5 20,5
Erro do meio de cada bloco (µm) +0,24 +0,26 +0,21 +0,25
Soma dos erros individuais (µm) +0,50 +0,46
(erro do comprimento nominal de montagem)
Erro do meio efetivo da montagem (µm) +0,47 +0,48
Erro resultante da montagem (µm) +0,03 +0,02
Tabela 2.2 – Erros resultantes da montagem de blocos cerâmicos.
Os resultados apresentados mostram que os erros da composição de um comprimento
pela aderência (montagem) de blocos cerâmicos é insignificante.
14

46. Figura 2.9: Blocos Padrão de Cerâmica: Estabilidade Térmica e Dimemsional.
2.6.6 Resistência Mecânica a Impactos
São altamente resistentes a quedas ou impactos em uso normal.
Os erros devidos às deformações superficiais provocadas por impactos ou rebarbas são
totalmente desprezíveis e facilmente removíveis.
MATERIAL
PROPRIEDADE CERÂMICA AÇO METAL DURO
(ZrO2)
Dureza (HV) 1350 800 1650
Coeficiente de
Expansão Térmica 10 ± 1 11,5 ± 1 5
(10-6 K-1)
Módulo de
Elasticidade 2,1 2,1 6,3
(x 105 N/mm2)
Fator de
Condutibilidade 0,00293 0,0544 0,0795
Térmica (J/mm.s.K)
Figura 2.10: Blocos Padrão: Propriedades Físicas e Mecânicas.
15

47. 2.6.7 Gravações
Em função de serem realizadas por um processo de laser, as gravações do
comprimento e do número de fabricação permanecem claras e nítidas durante um longo
tempo (praticamente toda vida útil do bloco), ao contrário do que acontece com seu
similar de aço que é sensível à corrosão.
2.7 MÉTODOS DE CALIBRAÇÃO DE BLOCOS PADRÃO
2.7.1 Método Diferencial
É o método mais simples e rápido para medir o erro do meio (Em) e a constância de
afastamento (CA).
No caso do Em, a calibração consiste em comparar um bloco com outro de classe de
erro superior, denominado de bloco de referência. Para este conjunto (referência) os erros
do meio são determinados através de calibração, que são executadas por laboratórios
credenciados. Conhecendo-se os erros do padrão de referência, os erros do bloco a
calibrar podem ser determinados.
Na figura 2.12 temos uma bancada de calibração de blocos padrão. Através de
medição diferencial, chega-se ao erro do meio do bloco a calibrar pela expressão:
Ec = Xc – ( Xp – Ep )
Sendo: Ec = Erro do meio do bloco a calibrar
Ep = Erro do meio do bloco de referência
Xp = Medida obtida no bloco à calibrar
Xc = Medida obtida no bloco de referência
Já no caso da constância de afastamento (CA), mede-se o comprimento do bloco
padrão em 5 posições ( figura 2.11). O erro de CA é a diferença entre o comprimento
máximo e mínimo determinados. Portanto, para sua determinação não é necessário a
utilização do bloco padrão de referência.
A fim de tornar a calibração mais rápida e confiável, o CERTI e o LABMETRO
desenvolveram um sistema automatizado de calibração de blocos padrão pelo método
diferencial.
Este sistema automatizado reduz o tempo de medição e confere confiabilidade à
calibração de blocos padrão de comprimento, orienta o operador durante o processo de
medição, realiza aquisição de dados, processa-os, compensa erros e gera documentação
dos resultados (certificado de calibração).
A calibração realizada tradicionalmente de forma manual, implica em:
- Registro manual dos valores das medições em planilhas;
16

48. - Processamento e comparação das medições de forma manual;
- Documentação externa e manual.
Este sistema automatizado tem como funções:
- Receber os dados nominais dos blocos padrão;
- Orientar e supervisionar o procedimento de medição;
- Efetuar automaticamente as leituras;
- Processar as leituras conforme uma metodologia adequada;
- Apresentar os resultados.
As características deste sistema são:
- Compensação do erro sistemático do bloco padrão de referência, correções de
comprimento devidos aos diferentes coeficientes de expansão térmica, bem como
erros de achatamento devido à diferença de material entre os blocos (referência e a
calibrar), permitindo que o trabalho de calibração tenha menor incerteza de medição
aumentando a confiabilidade dos resultados;
- Emissão de relatórios apresentando:
. erros do meio;
. desvios máximo e mínimo;
. constância de afastamento;
. classe de erro, segundo norma pré-definida, na qual o bloco padrão se enquadra
em função dos erros medidos;
- Pequena interferência do operador no processo de medição, não exigindo maior
especialização do mesmo, pois o sotware é extremamente simples de ser operado;
- Importante economia de tempo, comparativamente ao processo manual;
- Criação de uma base de dados diferenciada por cada conjunto de bloco padrão
calibrado.
Figura 2.11: Método Diferencial.
17

49. 2.7.2 Método Interferométrico
a) Medição do Erro de Planicidade
A planicidade das superfícies de medição é verificada utilizando-se o efeito de
interferência luminosa. Sobre a superfície do bloco padrão coloca-se um plano óptico
(placa de vidro altamente plana). De acordo com o caráter de desvios da planicidade
aparecem diversos padrões de franjas de interferência. Na figura 2.12a, tem-se a
configuração de franjas correspondente a uma superfície convexa. Na figura 2.12b, a
superfície é cilíndrica, e com um defeito (risco) local. Na figura 2.12c, tem-se um padrão
de franjas bom: sendo poucas, é claro que a inclinação não é grande e além disso, o
paralelismo e retilineidade das franjas prova a planicidade. As extremidades quebradas
das franjas correspondem a uma faixa marginal de largura de 1 mm no máximo, que
representa uma região de segurança que não pode ser usada para a medição. A figura
2.12d mostra a superfície levemente convexa. Ao se usar a luz monocromática, cujo
comprimento de onda (λ) é conhecido (por exemplo cor amarelo-laranja de sódio tem λ
= 0,575 µm), uma distância entre franjas que corresponde a diferença em altura dos
referidos lugares em λ /2 pode ser calculada numericamente. Assim, na figura 2.12d, o
afastamento entre os pontos 1 e 2 na direção ortogonal ao plano óptico é λ /2 ( no caso
da luz de sódio acima lembrada), o afastamento é (0,28 µm) e a distância entre os
pontos 1 e 3 é dois terços da distância entre as franjas vizinhas, ou seja:
( 2/3 ) . ( λ/2 ) = λ/3= 0,19 µm
Esta medição pode ser realizada através de um sistema completamente automatizado,
sem contato para medição de planicidade de superfícies altamente planas. Foi
inicialmente idealizado para medição de planicidade de blocos padrão, porém com
pequenas variações pode ser expendido para medição de paralelismo, ortogonalidade, e
constância de afastamento e possivelmente com aplicações em superfícies não planas,
tais como superfícies esféricas, cilíndricas e outras.
Este sistema utiliza um laser de HeNe e se baseia em princípios interferométricos e tem
a particular vantagem de não envolver componentes ópticos de precisão, uma vez que
aberrações ópticas são identificadas e corrigidas por software.
Os erros de repetitividade deste sistema podem chegar a 0,01 µm (figura 2.13).
b) Medição do erro do Meio
Para verificação do Erro do meio do blocos padrão (essencialmente os de classes de
erro 00 e K) utiliza-se a interferência luminosa. No processo trabalha-se com um sistema
padrão de medição baseado no comprimento de onda de um luz monocromática. O erro
máximo deste sistema padrão é de ± (0,02+L/5000) µm, ou seja, um valor quase
metade de um casa decimal melhor que o erro máximo no bloco padrão.
18

50. Figura 2.12: Controle da Superfície de Medição de Bloco Padrão.
Figura 2.13: Medição Automatizada da Planicidade.
19

51. Capítulo 3
PAQUÍMETRO
3.1 ASPECTOS GERAIS
3.1.1 Definição
O Paquímetro (figura 3.1) é o resultado da associação de: uma escala, como
padrão de comprimento; dois bicos de medição, como meios de transporte do
mensurando, sendo um ligado à escala e outro ao cursor; um nônio como interpolador
para a indicação entre traços.
3.1.2 Características Construtivas
Na figura 3.1a tem-se um paquímetro universal (com bicos para medições internas
e lingueta) e na figura 3.1b um paquímetro simples, porém com parafuso de chamada
que serve para ajuste fino da posição do cursor.
Os paquímetros distinguem-se pela faixa de indicação, pelo nônio, pelas
dimensões e forma dos bicos.
Em geral os paquímetros são construídos para faixa de indicação 120 ... 2000
mm; o comprimento dos bicos de 35 a 200 mm correspondentemente. Para casos
especiais é possível adquirir paquímetros de bicos compridos.
O material empregado na construção de paquímetros é usualmente o aço com
coeficiente de dilatação linear α = 11,5 µm/m.K, de forma que o mesmo tenha
comportamento térmico equivalente à maioria das peças.
As superfícies dos bicos situadas frente a frente destinam-se às medições externas
(figura 3.1). Para medições internas, os extremos dos bicos são rebaixados, com
superfícies externas cilíndricas. Ao usar-se estas superfícies de medição, deve-se
adicionar à indicação a espessura dos ressaltos dos bicos que é, geralmente, um valor
arredondado (10 ou 20 mm). Importante é realizar a calibração desta distância
periodicamente a fim de determinar o seu valor efetivo e fazer a correção do erro
durante o processo de medição.
Nos paquímetros universais os bicos para medições internas são prolongados para cima
e apresentam a forma de gumes, o que permite medir dimensões menores do que
aquele valor arredondado.
Paquímetros pequenos podem ter, na parte traseira, uma lingueta que se move
junto com o cursor e serve para medir profundidades.
1

52. Figura 3.1: Paquímetros: Tipo universal e de Ajuste Fino.
3.1.3 Tipos de Paquímetros
Além do tipo universal, o paquímetro pode ser apresentado de diversas formas
específicas para cada uso:
- paquímetro de profundidades (figura 3.2a);
- calibrador de espessura de dentes de engrenagens (figura 3.2b);
- graminho (paquímetro de altura) (figura 3.2c) ;
- paquímetro para rasgo de chaveta (figura 3.2d).
Além destes tipos existem muitas outras variantes, no formato e tamanho dos bicos,
da faixa de indicação, etc.
A escala de um paquímetro poderá ser (figura 3.6):
- mecânica com indicação via nônio;
- cremalheira com indicação via sistema relógio comparador;
- magnética ou eletroóptica, com indicação eletrônica e indicação digital.
2

53. F i g u r a 3 . 2 : P a q u í m e t r o s E s p e c i a i s.
s
3.1.4 Aspectos Operacionais
Nas medições externas recomenda-se colocar a peça a ser medida o mais perto
possível da escala, de modo a minimizar os erros de não obediência do princípio de
Abbé. Nas medições internas, antes de fixar o cursor, deve-se afrouxar a pressão de
medição.
Em geral, na medição com paquímetro, deve-se evitar um aperto forte dos bicos
sobre a peça (evitar a força de medição excessiva).
Além disso, deve-se evitar, ao máximo possível, movimento relativo entre os bicos
e peça, já que isto provoca desgaste dos bicos, e assim a geração de erros de medição
com o paquímetro. Sob hipótese alguma, deve-se medir uma peça em movimento (por
exemplo: no torno).
O paquímetro universal (ou quadrimensional) pode ser aplicado de diversas formas
(figura 3.7).
Com um paquímetro comum é possível medir diâmetros maiores do que o seu
curso. O paquímetro é colocado na peça a ser medida conforme mostra a figura 3.8; b
é o comprimento dos bicos e A é a indicação no paquímetro. Diâmetros maiores ou
segmentos podem ser medidos com o uso de Blocos Padrão. Sendo a = A/2, temos que
o raio da peça é dado por
a 2 +b 2
R =
2b
3

54. Alguns paquímetros digitais podem ser interfaceados a pequenas impressoras
com módulos estatísticos ou até a microcomputadores, onde os dados podem ser
processados rapidamente, facilitando o trabalho dos cálculos intermediários em
operações mais complexas como as vistas na figura 3.8.
F i g u r a 3 . 3 : P a q u í m e t r o s A n a l ó g i c o s.
s
Figura 3.4: Paquímetros com nônio.
4

55. Figura 3.5: Paquímetros Digital.
Figura 3.6: Paquímetros: Tipos de leitura.
3.2 COMPORTAMENTO METROLÓGICO
A leitura do nônio deve ser realizada com o paquímetro perpendicular à vista do
operador para evitar o "erro de paralaxe". Entretanto, a maioria das pessoas possui
maior acuidade visual com uma das vistas, o que provoca um erro associado ao
processo de leitura. Por isso, recomenda-se fazer a leitura com uma só das vistas, apesar
das dificuldades em encontrar-se a posição certa. Em experiência feita com um grupo de
mecânicos, constatou-se que as indicações feitas em paquímetros de precisão, abertos
em uma dada dimensão, apresentaram uma dispersão de ± 0,02 mm.
A incerteza de medição de um paquímetro depende:
- dos erros da divisão da escala principal;
- dos erros da divisão do nônio;
- da retilineidade dos bicos de medição;
- da perpendicularidade dos bicos de medição em relação à haste e paralelismo
entre si;
- dos erros da guia do cursor.
5

56. Na medição correta com blocos padrão, num ponto qualquer, as indicações no
nônio só podem diferir do valor do bloco padrão de um valor no máximo igual ao erro
admissível indicado na norma DIN 862, válida para paquímetros de qualidade. Os
erros admissíveis estão fixados em função apenas do comprimento medido.
A calibração para determinar os erros em operação de medição externa, é
realizada com blocos padrão, em vários comprimentos de modo a abranger diversas
posições das escalas principal e do nônio. É recomendado que esta calibração seja
feita nas posições interna, média e externa dos bicos, com força de medição constante.
As normas recomendam, entre outras características, tolerâncias da seguinte
ordem:
- planeza dos bicos para medições externas: 10 µm/100 mm;
- paralelismo das superfícies dos bicos: 15 a 20 µm.
Como normas que fixam as características dos paquímetros e regem os
procedimentos de qualificação citam-se:
- internacional : ISO 3599 (Vernier Callipers reading to 0,1 and 0,05 mm)
ISO 6906 (Vernier Callipers reading to 0,02 mm)
- brasileira : NBR 6393
- alemã : DIN 862
F i g u r a 3 . 7 : A p l i c a ç õ e s u s u a i s d e p a q u í m e t r o s.
s
6

57. F i g u r a 3 . 8 : A p l i c a ç õ e s u s u a i s d e p a q u í m e t r o s.
s
7

58. Capítulo 4
MICRÔMETROS
4.1 INTRODUÇÃO
Há poucas décadas atrás o micrômetro era considerado o principal instrumento de
medição de comprimento.
Os micrômetros foram os primeiros instrumentos que atenderam ao princípio de
ERNEST ABBÉ. As máquinas de medir modernas operam com o mesmo princípio do
micrômetro , ou seja, são construídas de forma a minimizar os erros de 1ª ordem e em
alguns casos até de 2ª ordem.
O desenvolvimento dos micrômetros deslanchou o avanço tecnológico na
fabricação de roscas e fusos de alta qualidade. Modernamente microprocessadores
estão sendo integrados à estrutura dos micrômetros, os quais executam, além da
medição de forma versátil, uma série de cálculos estatísticos.
4.2 PARAFUSOS DE MEDIÇÃO
Um fuso roscado possui, da mesma forma que uma escala, uma divisão contínua e
uniforme, representada pelos filetes da rosca. Num fuso roscado de 1 mm de passo, o
afastamento de um filete para o seguinte é de 1 mm; ele corresponde, portanto, a uma
escala dividida em milímetros. A tomada de medida é efetuada girando o fuso na porca
correspondente, obtendo-se entre estes elementos um movimento relativo de um passo
para cada volta completa. Frações de passo podem ser obtidas, subdividindo-se uma
volta completa em tantas partes quantas se queira.
O movimento axial do fuso ou da porca, determinado pelo número de voltas,
pode ser usado para alterar o afastamento entre duas superfícies de medição de um
determinado valor, como se verifica, por exemplo, nos micrômetros.
Como já referido, o movimento longitudinal pode ser realizado quer pelo fuso quer
pela porca, o mesmo pode-se dizer do movimento giratório. Nos parafusos de medição,
ambos os movimentos são realizados geralmente pelo fuso. A face frontal do fuso,
normal ao eixo do mesmo, constitui usualmente uma superfície de medição. O fuso leva
um tambor com divisões na periferia, no qual são lidas as frações de volta.
Os erros do movimento de avanço de um fuso de medição que corresponde aos
erros de divisão de uma escala, depende de diversos fatores:
- os erros do passo da rosca;
- do perpendicularismo dos sensores de medição em relação ao eixo do parafuso de
medição;
1

59. - da planicidade dos sensores de medição;
- do paralelismo dos sensores de medição
- da cilindricidade do tambor de leitura;
- do erro da divisão do tambor.
Em primeiro lugar, deve-se citar os erros do passo da rosca. O passo pode estar
afetado de erros, que se somam de filete, denominados " erros progressivos ". O valor
destes erros, só se verifica depois de uma ou mais voltas completas, embora
evidentemente afetem também comprimentos que não correspondem a uma volta
completa. No espaço de uma volta há, entretanto, erros na rosca que perturbam a
uniformidade do avanço. Como estes erros se repetem de volta em volta, denominam-se
" erros periódicos ".
Os erros de fuso de medição dependem destes dois tipos de erros, isto é, dos erros
" progressivos " e " periódicos ". Como hoje se pode executar roscas de elevada
qualidade, considera-se em geral, o erro global.
Para minimizar os erros de um sistema que utiliza parafuso micrométrico, ajusta-se
o zero do instrumento de forma a indicar o valor Eo ( figura 4.1), que corresponde ao
erro relativo à " linha zero ". Esta linha é localizada de forma a melhor distribuir os erros
globais em torno de si. Ele pode ser colocada simetricamente em relação aos erros
máximos e mínimos ( figura 4.1) ou ser a linha média ( aritmética ou quadrática ) dos
erros sistemáticos globais.
Figura 4.1: Ajuste do ponto zero de um parafuso micrométrico.
A norma ISO 3611, que especifica os limites de erros permissíveis para micrômetros
externos, permite um erro residual de zero. Por exemplo, um micrômetro de 0 - 25 mm
pode apresentar valor Eo igual a ± 2 µm.
Um outro erro pode ocorrer no fuso de medição em virtude do " curso morto ".
Designa-se desta forma a folga entre as roscas do fuso e da porca, o que se exterioriza
pela parada do fuso por uma determinada fração de volta, por ocasião da inversão no
sentido de giro. A fim de eliminar a influência do " curso morto " sobre os resultados de
medição, o movimento final do fuso durante a medição deve ser sempre no mesmo
sentido, o que na maioria das vezes acontece na pratica.
2

60. A aplicação mais conhecida da rosca como porta-medida encontra-se no
micrômetro.
4.3 MICRÔMETROS
Na figura 4.2 encontra-se o desenho, com cortes parciais, de um micrômetro junto
com a denominação das partes principais do mesmo.
O micrômetro têm como porta-medida um fuso roscado, cujo passo deve
corresponder em precisão e grandeza aos objetivos da medição. Os micrômetros tem
em geral um passo de 0,5 mm. O deslocamento longitudinal para uma rotação
completa do parafuso é portanto 0,5 mm. Existem micrômetros cujo parafuso possui
uma rosca com passo de 1 mm.
Figura 4.2: Micrômetro simples.
Os materiais empregados para fabricação do parafuso micrométrico são: aço
liga ou aço inoxidável. O aço inoxidável confere ao parafuso micrométrico maior
resistência à oxidação, mas por outro lado, a sua dureza é menor quando comparada a
um fuso de aço liga.
Os parafusos micrométricos são retificados, temperados e estabelecidos com
dureza de aproximadamente 63 HRc para garantia da durabilidade do mesmo.
O tambor graduado está fixado ao fuso micrométrico executando assim o mesmo
movimento como aquele. A fim de determinar o deslocamento longitudinal do fuso de
medição, na parte dianteira do tambor acha-se gravada uma escala que subdivide uma
rotação ( deslocamento de 0,5 mm ) em 50 partes. O deslocamento de uma divisão de
escala no tambor corresponde a um deslocamento longitudinal de 0,01 mm.
O tubo graduado possui duas outras escalas lineares que indicam os milímetros e
os meios milímetros. Estando o micrômetro ajustado, isto é, quando o traço do limite
inferior da Faixa de Medição ( FM ) coincidir com o traço zero no tambor graduado,
com os sensores de medição se tocando ( FM até 25 mm ), ou em contato com uma
3

61. haste padrão de comprimento ( FM maior que 25 mm ) então o mesmo pode ser
empregado para realizar medição, dentro de sua faixa de medição, com divisão de
escala de 0,01 mm. O tubo graduado pode apresentar ainda outra escala auxiliar,
geralmente com 10 divisões que é o nônio. Neste caso a resolução de leitura para o
micrômetro é dada pelo próprio nônio e vale 1 µm.
A resolução comumente adotada em micrômetros quando o mesmo não possui
nônio é igual a 1/5 da divisão de escala, ou seja 2 µm. Nos micrômetros digitais a
resolução é equivalente ao incremento digital, que em geral é 1 µm.
É importante salientarmos que a resolução não deve ser confundida com a
incerteza de medição (erro máximo ) do micrômetro, sendo esta última determinada pela
calibração do mesmo.
A trava do parafuso micrométrico permite fixar a haste de medição em qualquer
posição arbitrária. Ela deve impedir o deslocamento do fuso quando acionada, sem
porém, deslocá-lo do seu eixo.
A catraca é ligada ao parafuso micrométrico possibilitando força de medição
constante. Se a força for superior à resistência da catraca, a mesma gira em
falso sobre o parafuso ( a catraca limita o torque transmissível ao fuso ).
As plaquetas fixadas ao arco devem possibilitar a fácil acomodação do
micrômetro na mão do operador e permitir o isolamento contra o calor transmitido pela
mesma, de modo a evitar erros na medição provenientes da dilatação térmica do arco.
A cromação do tubo e do tambor de medição aumentam a resistência ao desgaste
e ataques pelos agentes químicos ( suor, óleo, etc. ). Procurando facilitar a leitura, a
cromação deve ser opaca, e não brilhante, para evitar reflexos.
Por estarem em contato com a peça a ser medida, os sensores de medição estão
sujeitos ao desgaste e por isso nas extremidades dos mesmos, emprega-se placas de
metal duro. Estas placas devem ser manuseadas com cuidado, pois o metal duro é
frágil. A dureza dos sensores é de aproximadamente 63 HRc. A qualidade da superfície
da peça também influenciará no desgaste dos sensores.
De importância capital para a minimização da incerteza de medição, são a
retificação e a lapidação paralela dos sensores.
O tubo graduado e tambor graduado ( figura 4.2 ) devem ser usinados com
tolerâncias estreitas e com forma geométrica cilíndrica, a fim de garantir concentricidade
para os diâmetros externos e interno. Com isto, tem-se rotação fácil para o tambor de
medição e leitura simplificada. Graças a uma pequena folga entre o tubo e o tambor,
evita-se ao máximo os erros de paralaxe.
A gravação dos traços sobre o tubo bem como sobre o tambor é feita em
máquinas especiais que permitem traçar divisões com mínimos erros e com grande
constância e nitidez, o que facilita a leitura. Algumas fábricas usam gravação inclinada
4

62. dos traços dos milímetros; assim é possível distinguir com maior facilidade os traços
referentes aos milímetros daqueles referentes aos meios-milímetros, já que o tambor não
oculta o traço.
No eliminador de folga, graças ao ajuste cônico sobre o guia do fuso, com o
aperto da porca consegue-se eliminar o curso morto, permitindo ainda deslizamento
suave ao girar o fuso.
O comprimento de medição do fuso é geralmente de 25 mm, podendo-se
encontrar também parafusos com 13 mm e 30 mm. O comprimento do arco cresce de
acordo com o aumento da faixa de operação do micrômetro, normalmente com
escalonamento de 25 mm, sendo pois, 0 a 25, 25 a 50, 50 a 75 mm, etc. Os
micrômetros de arcos são construídos para diâmetros de até cerca de dois metros (2 m).
O arco é construído com aço forjado ou ferro fundido especial. O arco deve estar
livre de tensões, e deve ser envelhecido artificialmente. A seção retangular em forma de
I, confere ao arco maior rigidez.
Para medidas grandes, a bigorna, e às vezes também o mecanismo micrométrico
são construídos de modo ajustável, permitindo faixas de medição maiores do que 25
mm, por exemplo, de 300 a 350 mm. Nestes casos deve-se ajustar a bigorna e o
mecanismo micrométrico de 25 em 25 mm, com auxílio de blocos padrão ou hastes
padrão calibradas.
4.3.1 Tipos de Micrômetros
Além dos micrômetros convencionais com sensores de medição planos, existem
micrômetros especiais com sensores de medição adaptados aos objetivos da medição.
São utilizados para as mais diversas operações como medição de roscas externas e
internas, módulos de engrenagens, rasgos de chavetas, etc.
Para medição do diâmetro de flancos ( diâmetro primitivo ) de roscas, utilizam-se
sensores de medição do tipo cone e prisma, cujas dimensões são adaptadas ao perfil da
rosca a controlar. A fim de evitar a necessidade de um micrômetro para cada passo e
para cada perfil da rosca, os sensores de medição de roscas são substituíveis ( figura 4.7
). Na mesma figura 4.7 tem-se também, o aspecto geral do micrômetro e um exemplo
de medição.
Na figura 4.8 tem-se diversos micrômetros especiais, inclusive para medição de
roscas internas, usando o mesmo tipo de sensores de medição tipo " cone e V ".
Outros tipos de micrômetros são os comparadores de roscas. Os sensores são cônicos
e fabricados especialmente para utilização em rápidas comparações da qualidade da
rosca em operações de usinagem de parafusos, e ainda para a medição de rasgos de
chavetas, rebaixos, ranhuras e muitas outras aplicações inacessíveis com micrômetros
comuns.
5

63. Figura 4.3: Micrômetro.
Figura 4.4: Micrômetro Digital.
Figura 4.5: Micrômetro Digital.
A medida sobre dentes de engrenagens ( valor médio sobre vários dentes ) pode ser
determinada com o micrômetro que tem os sensores de medição em forma de discos
rasos ( figura 4.8). É empregado também para medição de ranhuras, aletas, rasgos de
chaveta e ainda outros materiais moles onde se faz necessária maior área de contato
( menores deformações do material ).
6

64. Figura 4.6: Usos para micrômetros.
Figura 4.7: Micrômetros para roscas, com pontas de medição
substituíveis.
Medidas de ressaltos e profundidades são efetuadas com um micrômetro de
profundidade ( figura 4.8 ), comumente equipado de um conjunto de hastes de vários
comprimentos que são parafusadas, intercambiavelmente, no corpo do micrômetro.
Quando o local é de difícil acesso geralmente usa-se micrômetros com meia base.
7

65. Figura 4.8: Micrômetros especiais.
Figura 4.9: Micrômetros interno com cabeça combinada.
Figura 4.10: Micrômetros de profundidade: exemplo de medição.
8

66. Figura 4.11: Micrômetros para canais: exemplo de medição.
Figura 4.12: Micrômetros interno tubular com quatro extensões.
Para medição de espessura de chapas numa posição afastada da borda é usado o
micrômetro de arco profundo ( figura 4.8 ).
9

67. Para medições externas existem também micrômetros com indicação " digital "
mecânica ou com cristal líquido, e ainda micrômetros com parafuso micrométrico
associado com relógio comparador montado no lugar da bigorna.
Para a medição de espessura de parede de tubos usa-se um micrômetro cuja
bigorna tem um sensor de medição abaulado ou esférico ( figura 4.16 ), a fim de
garantir o contato bem definido entre o sensor de medição e a peça a medir ( Exemplo:
tubo ).
Figura 4.13: Micrômetros de profundidade.
Figura 4.14: Micrômetros de profundidade.
10

68. Figura 4.15: Usos para micrômetros de profundidade.
Figura 4.16: Micrômetros especiais.
Micrômetros para medidas internas possuem ponteiras de medição ( figura 4.16 ),
assemelhando-se até certo ponto aos paquímetros.
Para medição de ferramentas de corte podem ser usados micrômetros especiais,
cuja bigorna em forma de prisma ( figura 4.16 ) com vários ângulos, permite a medição
de ferramentas com um número ímpar de dentes, o que é o caso comum. Para um
número par de dentes a medição poderia ser efetuada sem problemas, utilizando um
micrômetro convencional, ideal para medir peças cilíndricas, possibilitando ao mesmo
tempo verificar a ovalização.
11

69. Figura 4.17: Micrômetros especiais.
Figura 4.18: Micrômetros para aplicações especiais.
Micrômetros para medidas de diâmetros internos de grandes dimensões são construídos
em forma tubular (para maiores faixas de medição) . Os micrômetros tubulares,
(figura 4.12), são comumente equipados com extensões. Deste modo com um único
corpo principal e quatro extensões pode-se medir numa faixa de 100 até 300 mm com o
mesmo parafuso micrométrico de 25 mm de faixa de operação. As superfícies de
medição I e II ( figura 4.12 ) encontram-se nas peças a e b. O diagrama na figura
4.12 mostra o princípio das combinações de extensões na faixa de 100 até 200 mm.
12

70. Micrômetros tubulares de vários sistemas de tubos telescópios são fabricados para
faixas de operação de até alguns metros.
Micrômetros com sensor fixo esférico são também utilizados para medir capas de
rolamentos, buchas, anéis, etc. ( figura 4.17a ).
Os micrômetros com sensores tipo faca ( figura 4.17b ) são utilizados para medir
ranhuras estreitas, entalhes, rasgos de chaveta e outras aplicações.
Para medição de ressaltos internos recomenda-se o micrômetro com arco curto
( figura 4.17c ).
Há também os micrômetros de medição de espessura e profundidade da solda e
rebordo em latas comuns e de aerosóis. São indispensáveis durante a fabricação e
imprescindíveis no envasamento de produtos gasosos, aerosóis, etc.
Para medição de diâmetros internos, os micrômetros são fabricados com três
sensores defasados de aproximadamente 120º, o que permite definir com segurança o
diâmetro a ser medido ( três pontos definem uma circunferência ).
4.3.2 Micrômetros Digitais
O micrômetro digital apresenta os elementos básicos do micrômetro
convencional, porém permitem a realização de medições com menor incerteza de
medição devido a facilidade de leitura no instrumento, diminuindo os erros de medição
associados principalmente a construção da escala e de paralaxe.
Os primeiros micrômetros digitais fabricados apresentavam resolução de
medição de 2 µm e eram puramente mecânicos. Micrômetros de fabricação modernos
são constituídos por um microprocessador e um mostrador ( display ) de cristal líquido. A
resolução destes instrumentos é de 1 µm ( figura 4.5).
A introdução do microprocessador e do mostrador de cristal líquido
revolucionaram todo o processo de medição com os micrômetros. Estes permitem:
- Zeragem do instrumento em qualquer posição do fuso permitindo medições
absolutas e diferenciais.
- Introdução de limites de tolerância na memória, permitindo identificar se a peça
satisfaz ou não as especificações de normas, fabricação, etc.;
- Análise estatística dos dados, informando o número de medições realizadas,
máximos e mínimos valores das medições, valor médio e desvio padrão das
medições;
- Saída para impressora, obtendo-se além dos parâmetros citados acima o
histograma relativo as medições.
13

71. Segundo especificações de fabricantes, as características metrológicas são:
- Resolução : 0,001 mm.
- IM (segundo fabricante)1: ± 2 µm para faixas de operação 0 - 25, 25 - 50 e 50 -
75 mm e 3 µm para faixa de operação de 75 - 100 mm.
- Planicidade dos sensores : 0,3 µm.
- Paralelismo entre os sensores: para micrômetros com faixa de 0 - 25 e 25 - 50 mm
é de 1µm e para faixas de 50 - 75 e 75 - 100 mm é de 2 µm.
- Força de medição : 6 a 10 N.
4.4 FONTES DE ERROS NAS MEDIÇÕES COM MICRÔMETROS
É importante o estudo das fontes de erros em micrômetros para sua minimização
durante o processo de medição.
Uma das grandezas físicas que mais influi sobre as medições é a temperatura.
Uma parcela do erro dos micrômetros se deve à transferência de calor no momento em
que o operador trabalha com o mesmo, segurando-o. Este procedimento causa erro de
leitura, desalinhamento dos sensores pela dilatação do arco, etc. Pode ser reduzido pelo
emprego de um plástico ( isolante ) no arco do micrômetro ou segurando o mesmo por
intermédio de um pedaço de couro.
Mais correto ainda é segurar o micrômetro num suporte especial que se fabrica
para este fim. ( A peça segura-se na mão esquerda ). O emprego de um suporte para
fixação do micrômetro é recomendado sempre que possível.
A incidência direta de luz solar, proximidade de um forno ou ventilador, são
também situações a evitar.
Outro problema comum é a deflexão do arco. A aplicação de uma força de
medição sem uso da catraca pode causar a deflexão do arco resultando na separação
das superfícies de medição. Além da deflexão do arco, forças excessivas provocam
deformações e achatamneto nas peças submetidas a medição, o que é uma fonte de
erro significativa.
O emprego da catraca, aliado a um movimento suave e lento garante força de
medição constante e com isto, resultados com pequena dispersão de medição.
Na própria medição, é necessário tomar cuidado para que a força de medição
seja igual aquela usada na ajustagem e que não seja demasiada ( o valor normalizado
é 5 até 10 N ). Por isso, o fuso deve se apertado lentamente ( sem impulso ) sempre por
1Na prática a IM, considerando-se a soma da tendência e da repetitividade, destes micrômetro é superior a
pelo menos ± 4 µm.
14

72. intermédio da catraca, deixando-se a mesma deslizar durante 3 a 5 voltas. A velocidade
de aproximação rápida dos sensores projudica os componentes do mesmo.
Erros de leitura por paralaxe são evitados lendo-se o tambor perpendicularmente.
Durante a medição não se deve empurrar o micrômetro sobre as superfícies
ásperas ou sujas. Também não se deve abrir o micrômetro para uma certa medida,
acionar a trava e forçá-lo sobre a peça como se fosse um calibrador de boca. Com este
procedimento tem-se um desgaste rápido dos sensores.
4.5. PROCEDIMENTO DE CALIBRAÇÃO
4 . 5 . 1 Cu i d a d o s I n i c i a i s
Antes de iniciar a calibração de um micrômetro, ou qualquer outro instrumento, há
a necessidade de uma rigorosa inspeção do mesmo no que se refere aos aspectos de
conservação, como por exemplo, verificação visual da qualidade da superfície dos
sensores, condição de funcionamento do instrumento, por exemplo catraca, trava, folgas
no parafuso micrométrico, etc., identificando-se a necessidade ou não de manutenção
corretiva prévia.
4.5.2 Normas Técnicas
Além da norma ISO 3611 a nível internacional, é importante destacarmos também
as normas existentes em alguns países, como por exemplo a NBR EB-1164 ( Brasil ),
DIN 863 ( Alemanha ), JIS B 7502 ( Japão ) e VSM 58050 ( Suíça ). Além delas, os
próprios fabricantes de micrômetros podem ter normas internas para qualificar seus
instrumentos.
4.5.3 Parâmetros a Serem Qualificados
A seguir são apresentados os parâmetros a serem verificados na qualificação de
um micrômetro.
a) Erros de indicação e repetitividade
Estes erros englobam os efeitos de todos os erros individuais, como por exemplo,
erro de passo do parafuso micrométrico, das faces de medição (planeza e paralelismo
dos sensores de medição), da construção da escala, etc, e sem dúvida é o item mais
importante a ser verificado. A calibração é executada ao longo de toda a faixa de
medição do instrumento.
O erro de indicação é determinado com o auxílio de blocos padrão classe I. É
fundamental que os blocos padrão estejam calibrados , de modo a garantiar a
confiabilidade dos resultados.
As normas citadas no item 4.5.2 especificam que os comprimentos dos blocos
utilizados na calibração sejam os seguintes : 2,5 - 5,1 - 7,7 - 10,3 - 12,9 - 15,0 - 17,6
15

73. - 20,2 - 22,8 e 25 mm. Com estes comprimentos é possivel detectar-se a influência dos
erros do parafuso micrométrico e do paralelismo para diferentes posicões angulares do
sensor móvel. O ponto zero ou o limite inferior da faixa de medição também é um ponto
de calibração.
Alguns fabricantes de blocos padrão já dispõem de um conjunto com os
comprimentos citados anteriormente, o que facilita em muito o trabalho do metrologista,
evitando-se a necessidade de realização de montagens com dois ou mais blocos. A
limpeza dos blocos, bem como dos sensores do instrumento é fundamental. Caso haja
necessidade de montagem dos blocos padrão, todo cuidado deve ser considerado
durante o procedimento de aderência dos mesmos a fim de evitar danos às superfícies
de medição.
Para micrômetros de faixa de medição superior a 25 mm, os comprimentos dos
blocos a serem utilizados como comprimento padrão na calibração são obtidos
pela a aderência (montagem) de um bloco, de comprimento equivalente ao limite
inferior da faixa de medição, aos blocos citados anteriormente. Como exemplo, para
fazermos a calibração de um micrômetro de 25 a 50 mm , devemos utilizar um bloco de
25 mm para aderir aos blocos do conjunto citado anteriormente de modo a obter-mos
os seguintes comprimentos: 25 / 27.5 / 30.1 / 32.7 / 35.3 / 37.9 / 40 / 42.6 / 45.2 /
47.8 / e 50 mm .
O erro máximo (por norma) para qualquer ponto na faixa de medição do
micrômetro é determinado por:
Emax=(4+L/50) (µm),
/2/
onde L é o limite inferior da faixa de operação em milímetros.
Infelizmente, como a grande maioria das normas técnicas, o valor do erro máximo
dado pela expressão matemática apresentada anteriormente só considera a parcela de
erros sistemáticos (tendência), como pode ser observado na figura 4.19. A parcela dos
erros aleatórios não é citada por estas normas, o que é uma deficiência das mesmas.
Como exemplo, um micrômetro de 0 - 25 mm não deve apresentar E max
superior a 4 µm (observe que neste caso L é igual a zero). Recomenda-se, após
calibração, construir uma curva de erros para o instrumento.
A interpretação deste erro é importante. A normas definem que o micrômetro deve
atender a dois requisitos simultâneos, e que serão comentados a seguir considerando-se
o processo de calibração de um instrumento com faixa de medição de 0-25 mm:
- a tendência, para cada ponto de calibração, não pode ser superior a 4 µm. Isto
significa que este erro pode assumir sinal positivo ou negativo ( ISO 3611 ) e;
16

74. - a máxima diferença entre as ordenadas da curva de erros, isto é, a diferença entre
a tendência máxima e mínima determinada na calibração não pode exceder a 4
µm (ver figura 4.19) ( DIN 863 ).
A primeira condição pode ser obtida quando ajustes de zero, ou limite inferior da
faixa de medição, podem contribuir para minimização dos erros. A segunda condição é
a mais problemática tendo-se em vista que não é possível nenhum tipo de correção.
Figura 4.19: Erro máximo de micrômetros segundo as normas
ABNT-EB 1164 e DIN 863.
A grande diferença entre as normas DIN 863 e ISO 3611 está com relação ao
ajuste do instrumento. A norma ISO permite uma tendência residual de zero, enquanto a
norma DIN exige que o instrumento seja ajustado obrigatoriamente de modo a
obter erro igual a "zero" no ponto zero ou limite inferior da faixa de medição.
b) Erros de paralelismo dos sensores
O erro de paralelismo dos sensores de micrômetros de 0 - 25 mm é determinado
pela observação das franjas de interferência geradas através da aplicação de um plano
óptico especial entre os sensores de medição do micrômetro. Para uma análise mais
ampla utiliza-se um conjunto de quatro planos ópticos, que se diferenciam pela
espessura escalonada de um quarto de passo /2/. O plano óptico deve estar paralelo à
superfície de um dos sensores ( franjas de interferência devem praticamente desaparecer
ou formar círculos concêntricos ). O número total de franjas não deve exercer a oito,
quando sob luz comum /2/.
Para micrômetros acima de 25 mm, utiliza-se um bloco padrão entre dois planos
ópticos, devidamente aderidos, para determinação dos erros de paralelismo.
17

75. Evidentemente o bloco utilizado deve ter erros de paralelismo entre as faces de medição
inferior a um décimo do erro de paralelismo tolerado para o micrômetro.
c) Erro de planeza dos sensores
O erro de planeza dos sensores de medição é determinado por meio de um plano
óptico, colocado de tal maneira que o número de franjas de interferência seja mínima
ou que existam círculos fechados. Para superfícies com tolerância de planeza de 0,001
mm, não mais do que 4 (quatro) franjas circulares e concêntricas da mesma cor devem
ser visíveis. As superfícies de medição devem ser lapidadas e cada superfície deve ter
planicidade dentro de 1 µm /2/.
d) Rigidez do arco ( estribo )
A rigidez dos arcos de micrômetros deve ser tal que uma força de 10 N aplicada entre
os sensores não provoque uma flexão que ultrapasse valores indicados por normas. O
controle é efetuado aplicando uma carga de 10 N no eixo de medição do arco /5/.
Figura 4.20: Padrões de comprimento para ajustagem de micrômetros.
e) Força de medição
A força de medição exercida pelo acionamento da catraca sobre a peça a medir
deve apresentar valores entre 5 a 10 N /2/. A força de medição pode ser medida por
um dinamômetro de alavanca, por exemplo.
f) Erro de ajuste do zero ou do limite inferior da faixa de medição
O micrômetro deve apresentar dispositivo para ajuste do zero e em geral, quando
para faixas de medição superiores a 0 - 25 mm, devem vir acompanhados de padrões
com dimensão igual ao limite inferior da faixa de medição do instrumento para
possibilitar o ajuste da escala.
Os padrões de comprimento para ajustagem de micrômetros externos são cilíndricos
e apresentam as superfícies de medição planas e/ou esféricas com raio
18

76. aproximadamente igual a metade do comprimento padrão (figura 4.20a). São
fabricados de aço ferramenta especialmente selecionado. As superfícies são temperadas
e lapidadas.
Para ajustagem de micrômetros de roscas pelo método do prisma-cone, os padrões
de comprimento apresentam-se com uma extremidade em forma de " V " e a outra em
forma de cone, permitindo o contato entre os sensores com o objetivo de simular uma
rosca comum ( figura 4.20b).
Anéis padrão são utilizados para ajustagem de micrômetros para medição de
diâmetros internos ( figura 4.20c).
Os padrões utilizados em ajustagem de micrômetros, devido ao seu desgaste com o
uso, devem ser calibrados periodicamente, isto é, devem ser determinados os seus
comprimentos efetivos de modo a não introduzirem erros sistemáticos, geralmente
significativos, sobre os resultados das medições. Este é um requisito importante para que
um micrômetro possa ser utilizado em controle de qualidade de peças ou medições em
geral.
Deve ser exigido por parte do solicitante do serviço um certificado de calibração
destes padrões, que deverá efetivamente relatar o erro sistemático do mesmo e a
respectiva incerteza de medição.
É permitido um erro de indicação de ajuste da escala, segundo ISO 3611, dada
pela seguinte equação:
± (2 + L/50) µm
sendo L o limite inferior da faixa de medição do instrumento em milímetros /2/. Assim,
por exemplo, para um micrômetro de 0 - 25 mm é permitido um erro residual no limite
inferior da faixa de medição igual a ± 2 µm .
Como comentado anteriormente no item a, a Norma DIN 863 não permite erros
residuais no limite inferior da faixa de medição.
g) Qualidade dos traços e algarismos
O micrômetro deve apresentar os traços de graduação nítidos e uniforme, regulares,
sem interrupção e sem rebarbas. A distância entre os centros dos traços da graduação
não deve ser menor que 0,8 mm /2/. O que evita muitos erros de leitura é a gravação
inclinada dos traços da escala sobre o tubo.
h) Erros devido ao acionamento da trava
Quando acionada a trava, a distância entre os sensores de medição não deve
alterar mais que 2 µm /2/.
19

77. 4.5.4 Intervalos de Calibração
As normas para qualificação de micrômetros não especificam o tempo entre
recalibrações. Recomenda-se que os micrômetros sejam calibrados de acordo com a
freqüência de utilização, baseado em levantamentos estatísticos resultando, por exemplo,
num regulamento de calibração parcial, diária, isto é, calibração no ponto zero e alguns
pontos da faixa de medição, alternando com calibrações completas e detalhadas em
intervalos semanais ou mensais. Esta periodicidade é necessária em função do rápido
deterioramento das características metrológicas em função do mal uso, choques, etc.
Importante citar a necessidade de manutenção ou substituição de instrumentos
danificados ou excessivamente desgastados devido ao uso.
Como intervalo inicial de calibração recomenda-se o período entre 3 a 6 meses,
dependendo evidentemente dos aspectos citados anteriormente.
Figura 4.21: Medição do erro de paralelismo dos sensores.
4.6 EXEMPLOS
O relatório anexo mostra o resultado da qualificação integral de um micrômetro.
Este exemplo caracteriza um instrumento de boa qualidade e bom estado de
conservação e dentro das especificações previstas pelas normas /1, 2/.
Alguns resultados referentes a um instrumento já recusado pelo Laboratório de
Calibração e retirado de uso, são apresentados a seguir, caracterizando-se os aspectos
que apresentam irregularidades segundo especificações das normas.
Nas folhas 1 e 2 ( TL 405 ) são apresentados os dados brutos/processados e o
gráfico da curva de erros. Como pode-se observar neste gráfico, o valor de Emax é
superior à tolerância estabelecida por norma.
20

78. Na figura 4.21 são apresentadas a franjas obtidas na medição do paralelismo dos
sensores de medição.
As curvas em forma de “S”, próximo às bordas caraterizam desgaste sofrido pelas
mesmas em função do atrito mecânico com as peças.
O estado superficial do sensor móvel é tal que impediu a formação de franjas de
interferência quando da avaliação de planicidade com o plano óptico ( superfície não
espelhada
A força de medição do micrômetro, quando o deslocamento angular do fuso é
dado através da catraca foi de ≅ 3N, não satisfazendo portanto as exigências das
normas.
4.7 REFERÊNCIAS BIBLIOGRÁFICAS
/1/ DIN 863 Meβschrauben. Bügelmeβschrauben Normalausführung:
Begriffe, Anforderungen, Prüfung.
/2/ ABNT EB 1164 Micrômetros externos com leitura em 0,01 mm.
/3/ KOTTHAUS, H. Técnica da Produção Industrial. Medição e controle. Ed.
Polígono, São Paulo; V.6, p. 44-8.
/4/ FARAGO, F. T. Handbook of Dimensional Measurement. Industrial Press INC. 2
ed, p. 19-26.
/5/ MAHR Längenprüftechnik. p. 16-40
/6/ PTB Diskussionstagung Längenmesstechnik, 03/74.
/7/ LEINWEBER, P. Taschenbuch der Längenmesstechnik.
/8/ SCHOELER, N. Metrologia e confiabilidade metrológica. CERTI. Março/95.
FIDÉLIS, G. C.
/9/ SCHOELER, N. Qualificação e Certificação de Instrumentos de Medição.
Abril/96.
FIDÉLIS, G. C.
21

79. Capítulo 5
MEDIDORES DE DESLOCAMENTO
5.1 INTRODUÇÃO
5.1.1 Importância
A medição de deslocamentos lineares e angulares é de fundamental importância
no campo da engenharia moderna. Cita-se como exemplos de aplicação:
- Movimentos em máquinas ferramentas, máquinas de medir, robôs industriais, etc.;
- Conversão mecânica/elétrica em transdutores para grandezas como: força,
pressão, torque, aceleração, etc.;
- Controle dimensional através da medição diferencial (pequenos deslocamentos)
como mais importante técnica de controle de qualidade automatizado;
Neste capítulo serão focalizados os medidores de aplicação mais corrente, e que
operam segundo princípios de transdução:
- Mecânico;
- Pneumático;
- Elétrico analógico;
- Elétrico digital.
5.1.2 Medição Diferencial
A produção em massa e de elevada qualidade na indústria mecânica exige
medição rápida, confiável e, se possível, com a mínima influência do operador. Estes
requisitos são preenchidos pela medição diferencial.
Os medidores de deslocamento, nesta aplicação, transformam um pequeno
deslocamento captado por um sensor de medição em um deslocamento amplificado de
um ponteiro, que possa ser lido num mostrador digital. O mensurando é portanto um
deslocamento linear, em geral, bastante pequeno.
Se o sistema de amplificação é de boa qualidade, pode-se obter facilmente
indicações da ordem de até décimos de micrometros (os medidores elétricos de
deslocamento podem oferecer resolução de até centésimos de micrometros).
A indicação representará sempre a diferença entre a dimensão da peça e a de um
padrão para o qual o sistema é ajustado.
A comparação se faz da seguinte maneira:
- Fixa-se o medidor de deslocamento em um dispositivo apropriado ( figura 5.1a );
1

80. - Coloca-se o padrão sob o sensor do medidor de deslocamento ( figura 5.1b ) e
"zera-se" a indicação, por exemplo, através do giro do mostrador até a
coincidência do ponteiro com o zero da escala ( figura 5.1c ), ou através do ajuste
da altura da fixação do apalpador utilizando dispositivo apropriado;
- Retira-se o padrão, coloca-se a peça e procede-se a leitura da diferença ( figura
5.1d ).
Figura 5.1: Medição diferencial.
Figura 5.2: Aplicações dos comparadores.
Especiais vantagens do método de medição são o seu pequeno erro e sua força de
medição quase constante. Como visto na descrição do paquímetro, pode-se cometer
erros consideráveis, devidos, por exemplo, a uma força de contato excessiva sobre a
peça. A medição diferencial permite eliminar alguns destes erros, pois o operador não
2

81. interfere na operação de medição, a não ser na ajustagem final do instrumento e na
colocação da peça a ser medida.
Modernamente a medição diferencial adquire crescente importância em função de
adequar-se amplamente à automatização com emprego de medidores elétricos de
deslocamento.
A medição diferencial tem também larga aplicação no trabalho de ajuste de
máquinas, como exemplificado a figura 5.2.
5.2 MEDIDORES MECÂNICOS
5.2.1 Sistema de Mola Torcional
Talvez o mais simples, mas o mais engenhoso dos medidores de deslocamento é o
instrumento projetado por Abramson. Na figura 5.3 é mostrado esquematicamente este
instrumento. É um sistema de alavanca associada a uma mola torcional tipo fita.
Uma fita muito fina (1) tem fixo no seu centro (0), um ponteiro muito leve (2). A fita
é torcida em forma de hélice em todo o seu comprimento. Uma extremidade da fita é
fixada em uma alavanca AOB angular tipo mola, um braço da qual é ligado
diretamente à haste do apalpador (4).
Quando a haste do apalpador se desloca, a alavanca angular gira em torno de 0
e provoca um aumento de comprimento na fita. Isto provocará um giro na fita e o
ponteiro girará de um ângulo proporcional ao alongamento da fita. Pode ser mostrado
que o fator de amplificação da fita é dado por:
d0 −9 , 1. 1
=
d1 W 2 .n
onde: 1 - comprimento da fita medido ao longo do seu eixo;
W- largura da fita;
n - número de voltas da fita;
0 - giro no ponto médio da fita em relação às extremidades.
Para que o instrumento apresente elevada sensibilidade, as dimensões da seção
transversal da fita devem ser bem reduzidas. Estas dimensões são da ordem de 6 x 2,5 µ
m e as tensões devidas à tração na fita, são normalmente aliviadas por pequenas
perfurações executadas ao longo do seu comprimento. Estes comparadores podem
atingir uma ampliação de 5.000 vezes.
A função da barra ajustável (3) é possibilitar o ajuste da amplificação. Isto é uma
grande vantagem do ponto de vista construtivo do instrumento, já que permite um último
ajuste em fábrica, ou na operação de manutenção.
As forças de medição, em geral, são de 2 a 3 N, podendo em alguns casos serem
reduzidas até 0,5 N.
3

82. Figura 5.3: Comparador com alavanca e mola tipo fita.
5.2.2 Relógios comparadores
São medidores de deslocamentos constituídos de um apalpador (que toca na
peça), de um mecanismo de amplificação baseado num sistema cremalheira/trem de
engrenagens e um mostrador circular onde desloca-se um ou dois ponteiros, à
semelhança de relógios.
Na figura 5.4 tem-se o mecanismo de um relógio comparador. Além dos
elementos básicos, estes medidores em geral possuem ainda:
- Mostrador giratório;
- Indicação de voltas completas do ponteiro;
- Eliminação de folgas nas engrenagens;
- Dispositivo "anti-choque";
- Compensação da força de medição.
Com respeito ao relógio comparador, faz-se ainda destaque aos seguintes
aspectos:
a) O mostrador giratório ( EP ) permite que o " zero " da escala principal, quando do
ajuste inicial do relógio comparador, seja levado a coincidir com o ponteiro,
qualquer que seja a posição do mesmo; desta maneira, a indicação inicial é zero,
facilitando em muito a operação de medição.
4

83. b) Além da escala principal ( EP ), os relógios comparadores costumam ser equipados
com uma escala auxiliar ( EA ), sobre a qual um ponteiro pequeno ( PP ) indica as
voltas completas do ponteiro principal ( P ), facilitando assim a leitura.
c) Para a eliminação de folgas do engrenamento, introduz-se uma protensão por
intermédio da mola espiral ( ME ). Pela ação desta mola que atua sobre a
engrenagem auxiliar ( EAX ), consegue-se que em todo o trem de engrenagens o
contato ocorra sempre no mesmo flanco dos dentes, qualquer que seja a direção do
movimento da haste ( H ). Assim elimina-se, em grande parte, o curso morto na
inversão do movimento do ponteiro ( histerese ).
d) A proteção do mecanismo contra o choque funciona da seguinte maneira: a
cremalheira (CR) não é usinada diretamente sobre a haste (H), mas sim sobre uma
bucha (BU) que, envolvendo a haste (H), pode deslizar sobre a mesma. Na situação
normal, bucha (BU) está pressionada pela força de protensão das engrenagens contra
o batente (BA) (pino transversal na haste H). Ocorrendo um impacto no apalpador, a
haste (H) se desloca livremente para cima e o batente (BA) se desprende do contato
com a bucha (BU), que permanece inicialmente sem movimentar-se; em seguida, sob
a atuação da força de protensão, a bucha (BU) começa a se deslocar lentamente
para cima até que o contato com o batente (BA) seja reestabelecido.
e) Compensação da força de medição: A mola de retorno (M) não atua diretamente
sobre a haste mas sim, por intermédio de uma alavanca (AL) (encostada
convenientemente, por exemplo, sobre o batente BA). Deste modo, graças à forma da
alavanca (AL) rotulada (em RO) o aumento da força da mola (M), devido ao
alongamento crescente da mesma quando a haste (H) sobe, é compensado pelo
decréscimo do braço B para b (sendo b < B) sobre o qual a força da mola atua.
Figura 5.4: Mecanismo de um relógio comparador.
5

84. Figura 5.5: Relógio comparador digital eletrônico.
5.3 MEDIDORES PNEUMÁTICOS
Os medidores pneumáticos de deslocamento prestam-se com particulares
vantagens para aplicações especiais em meios sob radiação nuclear ou campos
magnéticos, no controle de qualidade dimensional e outras. Na figura 5.6 apresenta-se
o princípio de funcionamento e um exemplo da realização prática do mesmo.
O método de medição pneumático consiste essencialmente em transformar um
deslocamento em variações de pressão de ar. O princípio é baseado no comportamento
do fluxo de ar em uma câmara com dois orifícios ( figura 5.6 ).
Figura 5.6: Princípio de funcionamento do medidor de deslocamento
pneumático.
O ar chega a uma pressão constante H. Passa através do orifício de controle G e
chega a câmara A. O tamanho do orifício G é constante, mas o tamanho efetivo do
orifício S pode ser variado através de um deslocamento d. Se d varia, varia também a
6

85. pressão h, o que nos fornece uma avaliação de d. Por dimensionamento dos diâmetros
de G e S e do rígido controle da pressão H, a pressão h poderá variar linearmente com
o tamanho efetivo do orifício S. Para valores h/H entre aproximadamente 0,6 e 0,8 a
relação entre a pressão h e a área do orifício S é linear. Estes valores são usados no
dimensionamento de todo o sistema. A lei linear entre a área do orifício S e a pressão h
é expressa na seguinte forma:
b. H
h = a. H − . A2
A1
onde: h -pressão na câmara A;
H -pressão de entrada;
A1 -área do orifício G;
A2 -área efetiva do orifício S;
a e b -são constantes
Como nos outros medidores, a sensibilidade é a relação entre a variação do sinal de
saída em relação a variação do mensurando. No caso, o sinal de saída é dh e a
variação do mensurando corresponde à variação de A2. Logo a sensibilidade é:
dh / dA2 = - bH / A1
Então a amplificação pneumática é proporcional a pressão de entrada e
inversamente proporcional a área (ou inversamente proporcional ao quadrado do
diâmetro) do orifício de controle (G).
É claro que um requisito necessário para este tipo de sistema de medição é a
pressão de entrada H ser rigorosamente constante. Para isto, deve-se ter um regulador
de pressão que controle a pressão de alimentação.
A figura 5.7 mostra um esquema do instrumento produzido pela Solex. O ar
comprimido provém de um compressor e passa inicialmente por um filtro. A seguir passa
por uma válvula de fluxo e onde a pressão é reduzida e mantida constante através de
um tubo mergulhado em uma câmara de água, sendo a pressão do tubo equivalente a
altura da coluna d'água. O excesso de ar escapa para a atmosfera em uma forma de
borbulhos.
O ar já com pressão reduzida para o valor H, passa através do orifício de controle
(3) e sai pelo orifício de medição (5). A resposta de pressão no circuito (h) é indicada
pela altura da coluna d'água no tubo manométrico. O tubo é graduado para indicar as
variações de pressão resultantes da variação do deslocamento d.
Amplificações de 50.000 vezes são possíveis neste sistema. A pressão H é
normalmente 500 mm H2O. Na prática, a variação da área efetiva de (5) pode ser feita
de três formas (figura 5.7 ):
7

86. - Por aproximação direta: a pressão varia conforme a posição do orifício de saída
em relação à peça a ser medida. É o caso dos bocais para a medição de
diâmetros internos.
- Por aproximação indireta: o furo de saída é substituído por um obturador em
forma de válvula e a saída de ar se efetua através do espaço entre o obturador e
seu encosto. Neste caso, o obturador é acionado mecanicamente através de um
apalpador e existe contato entre a peça e instrumento de medida.
- Por estrangulamento: a seção de saída é a própria peça a medir como por
exemplo o gigleur de um carburador.
Figura 5.7: Medição de deslocamento pelo princípio pneumático.
Figura 5.8: Forma construtiva dos tampões.
Uma das aplicações mais importantes dos medidores pneumáticos é sem dúvida a
medição diferencial de diâmetros internos de peças. Através de técnicas especiais de
construção dos sensores, denominados tampões ( figura 5.8 ), consegue-se um
instrumento bastante simples de operar, de elevada confiabilidade e pequena incerteza
de medição .
8

87. Uma outra forma construtiva é mostrada na figura 5.9. Neste sistema opera-se de
modo diferencial, isto é, o sinal proporcional é gerado em função da diferença de
pressão entre a câmara padrão (canal de referência) e a câmara do medidor (canal de
medição).
A medição de pressão é feita com manômetros diferencial que pode operar
mecanicamente ( figura 5.9 ) ou eletricamente com as consequentes vantagens.
Figura 5.9: Medidor pneumático (segundo Federal).
5.4 ELÉTRICOS ANALÓGICOS
Os medidores elétricos de deslocamento estão sendo cada vez mais utilizados em
substituição aos sistemas mecânicos e pneumáticos, principalmente pela sua
simplicidade de construção e facilidade de automatização.
Os transdutores eletro analógicos, segundo seu princípio de funcionamento se
dividem em:
- Resistivos;
- Indutivos;
- Capacitivos;
- Fotoelétricos.
A crescente evolução na área eletrônica permite que sejam construídos sistemas de
medição com erros mínimos e alta imunidade a fatores ambientais.
5.4.1 Resistivos
Os transdutores à base da variação da resistência, por alteração dimensional do
resistor efetivo, também conhecido por potenciômetros ( figura 5.10 ), encontram
9

88. frequente aplicação em função do seu baixo custo, sendo apropriados para
deslocamentos lineares e angulares. Apresentam como desvantagem a alteração de suas
características com o uso acentuado em função do desgaste. Não apresentam interesse
no campo de controle geométrico.
Figura 5.10: Transdutores resistivos de deslocamento.
5.4.2 Indutivo
Os medidores eletroindutivos de deslocamentos são os mais usados atualmente
dentre os medidores analógicos. Suas principais vantagens são:
- construção compacta;
- elevada resposta dinâmica;
- alta sensibilidade;
- boa linearidade;
- pouco desgaste;
- boa imunidade às influências de fatores ambientais.
Basicamente distingue-se dois métodos de variação da indutância de um
transdutor:
- variação da indutância própria;
- variação da indutância mútua entre dois indutores.
Na sequência são analisados alguns aspectos construtivos e operacionais dos
medidores do tipo indutivo:
a) Indutância própria (auto-indutância)
10

89. Ao tomar-se uma bobina de resistência elétrica desprezível e injetarmos nela uma
corrente elétrica variável no tempo, será criada uma diferença de potencial sobre esta
bobina (figura 5.11a), dada por:
d.i
v = − L.
d.t
A constante de proporcionalidade L entre a tensão e o oposto da derivada da
corrente em relação ao tempo é chamada indutância (unidade no SI=Henry). O
elemento físico que apresenta uma indutância predominante é chamado indutor ( figura
5.11d).
Figura 5.11: Indutância própria e indutância mútua.
b) Indutância mútua
Uma característica importante dos indutores é a indutância mútua. A indutância
mútua é a propriedade de um indutor percorrido por uma corrente elétrica com
amplitude variável, induzir uma tensão elétrica em um outro indutor próximo (figura
5.11b).
Um transformador de tensão é um conjunto formado por dois indutores acoplados
magneticamente de forma eficaz, ou seja, através de um núcleo de alta permeabilidade
magnética (figura 5.11c).
c) Características de um indutor
A forma fisica característica de um indutor é uma bobina enrolada sobre um núcleo
de alta permeabilidade magnética.
11

90. A indutância de um indutor ideal pode ser dada em função das características
geométricas da bobina, da permeabilidade magnética do meio, e do número total de
espiras ( figura 5.11d), ou seja:
L = n 2 . 1. A . µ
onde: n - número de espiras da bobina por unidade de comprimento;
1 - comprimento da bobina;
A - área da seção transversal da bobina;
µ - permeabilidade magnética do meio.
Cosiderando que N = n.l, onde N é o número total de espiras tem-se:
A
L = N2. .µ
1
A princípio qualquer um dos parâmetros da equação acima pode ser usado para
variar a indutância do indutor. O parâmetro mais usado, pela facilidade de construção
do transdutor e dos ótimos resultados metrológicos e operacionais alcançados é a
permeabilidade magnética "µ".
d) Transdutor Diferencial pela Auto-indutância
Na figura 5.12a pode-se ver um transdutor indutivo de variação da indutância
própria constituído de um só indutor. Este tipo de transdutor possui uma característica
altamente não linear. Como forma de compensar esta característica, usa-se o artifício da
ligação diferencial ( figura 5.12b), conseguindo-se uma resposta de maior sensibilidade
e linearidade.
Na figura 5.12b está mostrada a configuração normalmente encontrada em
medidores de deslocamento indutivo com contato, pela variação da indutância própria
de forma diferencial, ou seja, variação da indutância de dois indutores, uma
aumentando e outra diminuindo de valor, simultaneamente.
Pela variação da indutância de um indutor conforme visto na figura 5.12, foram
desenvolvidos diferentes tipos de transdutores de deslocamento indutivos. O transdutor
mais difundido é o deslocamento linear com cursor (contato). Na figura 5.13, tem-se a
forma construtiva de um tipo comercial. A faixa de medição é função das dimensões dos
componentes, atingindo a faixa de até ± 0,5 m.
Suas principais vantagens são robustez, erros mínimos, estabilidade e resolução,
que pode, dependendo da unidade de tratamento do sinal, ser até da ordem de 0,01 µ
m.
As principais características metrológicas e operacionais deste tipo de transdutor
podem ser vistas no quadro da figura 5.14.
12

91. Figura 5.12: Transdutor indutivo.
Figura 5.13: Transdutor indutivo com contato.
e) Transdutor Diferencial de Indutância Mútua
Este tipo de transdutor baseia-se no princípio de variação da indutância mútua
entre dois indutores. O tipo mais comum está mostrado na figura 5.15. É formado por
três indutores, sendo que um (primário) é excitado com uma tensão de amplitude e
13

92. frequência fixas e os outros dois ligados de forma diferencial (secundário). A tensão
nestes dois enrolamentos é proporcional ao fator de acoplamento entre o enrolamento
primário e secundário o qual varia de acordo com a posição do núcleo.
Característica Valor Típico Observações
Classe de 0,5% do V.F.E. Para a faixa de operação nominal.
Precisão
Linearidade 0,05% a 5% Dependendo da faixa de operação.
Incerteza de + 0,01 µm ± 2S (S= desvio padrão para
Medição n medidas) para uma faixa de ± 2 mm.
Histerese 0,003% mm Dados de calibração feita em um transdutor.
Resolução 0,01 µm Dada aproximadamente pela tensão
residual do circuito ponte.
Sensibilidade 100 mv / mm Por unidade volt de excitação do
transdutor.
Figura 5.14: Características metrológicas e operacionais
(valores limite típicos do transdutor de deslocamento de indutância
própria).
Figura 5.15: Transdutores indutivos ; Transformador diferencial.
f) Transdutor Indutivo sem Contato
Os transdutores indutivos sem contato permitem a medição de deslocamentos com
a vantagem de não provocarem retroação sobre o processo devido a inexistência de
força de medição. Existe no entanto a desvantagem de necessitar uma calibração para
cada montagem específica, já que o comportamento depende do posicionamento
espacial dos elementos envolvidos, bem como das características geométricas e do
material da peça da qual se está medindo o deslocamento ( figura 5.16).
14

93. Figura 5.16: Transdutores indutivos sem contato.
Os transdutores de deslocamento indutivos sem contato são utilizados aos pares,
podendo-se proceder a montagem com dois elementos ativos (1/2 ponte), na forma
diferencial, ou com um elemento ativo e um de compensação (1/4 de ponte).
g) Diagrama de Blocos do Sistema de Medição Eletro Indutivo
Na figura 5.17 pode-se ver o diagrama de blocos básico de um sistema de
medição de deslocamento utilizado com um transdutor indutivo do tipo com contato e
variação da indutância própria. Nesta figura pode-se ver inclusive os sinais obtidos nas
diversas etapas do sistema desde a grandeza a medir (GM) até a indicação do sinal
medido.
h) Transdutor Indutivo sem Contato, por Correntes Parasitas
Estes transdutores aproveitam o efeito de correntes parasitas (correntes de Foucauld)
que surgem em um material condutor de eletricidade quando este é submetido a um
campo magnético. O sensor é constituído de uma bobina ativa, que gera tal campo, e
outra que permite compensar variações de temperatura ( figura 5.18). Uma parte do
campo magnético de alta frequência (1 MHz) é dissipado no interior da peça, e esta
perda depende, entre outros fatores, da distância entre ela e a bobina. Um circuito em
ponte detecta esta perda, fornecendo um sinal elétrico que deve ser adequadamente
tratado. Os principais fatores que influenciam a sensibilidade são:
- Condutividade elétrica do material: obtém-se maior sensibilidade quanto maior a
condutividade, podendo-se ter materiais de baixa condutividade magnética (p. ex.:
alumínio);
- Distância entre a bobina e a peça: consequência da não linearidade do princípio
físico de transdução;
15

94. - Geometria da peça - a superfície sobre a qual incidem as linhas de campo
magnético, existindo restrições quanto à mínima espessura da peça (1 mm).
Estes sistemas devem ser calibrados para as específicas condições de utilização. No
sentido de compensar a não linearidade, estes sistemas contam com circuitos analógicos
de compensação, ou até mesmo, microprocessadores que permitem uma calibração e
ajustagem para cada aplicação.
Figura 5.17: Medidor indutivo de deslocamento ; Módulos do sistema
de medição.
5.4.3 Capacitativo
Conforme mostrado na figura 5.19, a capacitância de um capacitador pode ser
alterada em função da variação do afastamento das placas, da área superposta de
placas e do dielétrico. Todos os três recursos podem ser utilizados para a medição de
deslocamentos, conforme esquematizado na figura 5.19.
A montagem diferencial de dois capacitadores é utilizada para obter-se
linearidade e alta sensibilidade na medição de pequenos deslocamentos ( figura 5.19).
Uma das vantagens do sistema capacitativo é permitir medições de deslocamentos
em meios sujeitos a grandes variações de temperatura.
16

95. Figura 5.18: Medidor indutivo de deslocamento ;
Tipo sem contato, por correntes parasitas.
Figura 5.19: Transdutores capacitivos ; Métodos de variação da
capacitância.
17

96. 5.4.4 Fotoelétrico
Os medidores fotoelétricos analógicos são formados por um substrato
semicondutor e um circuito elétrico complementar ( figura 5.20 ). Eles fornecem um sinal
∆
de tensão "V", proporcional à posição do feixe luminoso ( d) incidente no substrato.
Possuem boa linearidade, boa sensibilidade e velocidade de operação entre 0 e 10 kHz.
Sua principal desvantagem é a de não poderem trabalhar em meios expostos à poeira,
óleo e outras impurezas.
Figura 5.20: Transdutor analógico fotoelétrico.
5.5 MEDIDORES ELÉTRICOS DIGITAIS
Os principais medidores elétricos digitais utilizam transdutores de deslocamento
que operam com escalas eletro-ópticas.
As escalas eletro-ópticas baseiam-se na codificação de uma barra ou disco por
marcações que interferem na transmissão de luz de uma fonte até um fotodetector. A
figura 5.21 mostra os dois princípios distintos de medição com as escalas eletro-ópticas:
o incremental e o absoluto.
Figura 5.21: Escalas eletroópticas incrementais.
18

97. 5.5.1 Medidores com Escalas Eletroópticas Incrementais
As escalas incrementais devido ao seu custo inferior e características metrológicas
superiores, têm uso predominante em aplicações práticas.
Opticamente elas podem ser de dois tipos:
- Reflexiva: um feixe luminoso incide sobre uma escala polida com gravações de
traços opacos, refletindo sobre ela em direção a um fotodetector. Com o
movimento da escala, este fotodetector libera um sinal elétrico proporcional à
intensidade luminosa incidente;
- Transparente: enquanto se desloca, uma escala de vidro gravada com traços
escuros interrompe de modo alternado um feixe luminoso entre a fonte e um
fotodetector (figura 5.21).
Em ambos os casos, o fotodetector fornece um sinal senoidal cujo período
corresponde ao espaçamento entre os traços da escala e que, após um tratamento, é
injetado em um contador. Com o número de pulsos contados e o espaçamento entre
franjas, é possivel calcular o deslocamento relativo da escala.
Figura 5.22: Medição opto-eletrônica de posição linear.
Uma maior resolução é obtida com um segundo conjunto de fotodetectores, cuja
posição em relação ao primeiro resulta na emissão de um sinal eletricamente defasado
em 90° (figura 5.22). Por uma combinação lógica dos níveis dos dois sinais, é possivel
interpolar deslocamentos menores do que o espaçamento entre franjas e identificar o
sentido do movimento. Traços adicionais, separados da escala principal, podem ser
previstos para definir uma posição de referência localizável quando se deseja inicializar
os contadores com um valor pré-estabelecido.
19

98. Algumas escalas têm gravados códigos correspondentes à posição absoluta da
escala, permitindo rapidamente recuperar a indicação no mostrador, após, por
exemplo, ter sido desligado o contador.
De maneira análoga às escalas lineares, configura-se escalas angulares com discos
ópticos e fotodetectores orientados radialmente.
Como principais vantagens destas escalas, apresentam-se a sua estabilidade com
o tempo e frente a variaçoes de temperatura, bem como a grande faixa de operação
que se pode obter pela justaposição de segmentos de escala. A principal fonte de erros
reside no espaçamento entre os traços e, com menor significado, erros de interpolação
entre duas franjas adjacentes.
Os sistemas de medição comerciais, baseados em escalas eletro-ópticas, têm sido
colocados à disposição com incremento digital de até 0,1 µm. A associação de
princípios interferométricos na detecção de franjas, estas agora gravadas em uma
camada de ouro depositada sobre uma fita de aço, permite alcançar uma incremento
digital de 0,02 µm.
5.5.2 Medidores com Escalas Eletroópticas Absolutas
Nas escalas absolutas existe uma codificação de posição gravada na sua
superfície, baseada em regiões que transmitem ou não o feixe luminoso de uma fonte
até um fotodetector ( figura 5.23 ). Um conjunto de fotodetectores capta, a cada
posição da escala, os sinais de passagem ou não do feixe nas diversas regiões
codificadas determinando-se a posição da escala pela combinação lógica destes sinais.
A principal desvantagem deste tipo de escala é a menor resolução que se pode
alcançar, muito embora já sejam disponíveis com sistemas com incremento digital de
1 µm.
Figura 5.23: Codificação absoluta de posição.
20

99. 5.5.3 O Laser Interferométrico
O laser interferométrico é um instrumento de grande versatilidade e qualidade
para a medição de deslocamentos lineares que vão de décimos de µm a dezenas de
metros. A seguir é descrito o seu princípio de funcionamento.
Um laser a gás He-Ne, tipo Zeemann, é o elemento central do Laser
Interferométrico modular. Ele pode alimentar simultaneamente até 6 módulos de
medição nos quais se mede, independentemente, uma grandeza por módulo.
Baseado na figura 5.24, pode-se expor resumidamente o princípio de
funcionamento. O laser emite um raio com duas frequências f1 e f2 bastante próximas e
estáveis. Pela deflexão de parte do raio sobre um fotodetetor, é gerado por interferência,
um sinal elétrico com uma frequência (f1 - f2). O restante da energia do raio é colocado
à disposição dos módulos. Na figura 5.24 está esquematizado um módulo genérico.
Figura 5.24: Componentes básicos do laser interferométrico modular.
O raio proveniente do laser é, num interferômetro, dividido em suas componentes f1 e
f2. Estes raios são, por sua vez, reencaminhados ao interferômetro pelos retro-refletores,
de onde seguem, conjuntamente, até o fotodetetor localizado no captador. Ali, gera-se
por interferência no estado estático dos componentes ópticos, um sinal de frequência (f1
- f2). Este sinal e o sinal de referência gerado no cabeçote, são encaminhados a
contadores eletrônicos dos quais é, ciclicamente, realizada a diferença, e esta transferida
a um acumulador. Havendo um movimento dos retrorefletores, ocorre uma alteração na
frequência (± ∆f1 e ou ± ∆f2) em função do efeito Doppler. O sinal gerado terá, então,
durante o deslocamento, uma frequência (f1 ± ∆f1) - (f2 ± ∆f2), sendo em função disto
registrada uma diferença nos contadores. O valor acumulado corresponde à diferença
do caminho óptico de f1 e f2.
No interferômetro linear (figura 5.25), um dos retrorefletores é fixo com relação ao
interferômetro (∆f2 = 0). Havendo um deslocamento dx do outro retrorefletor, a
diferença do caminho óptico entre f1 e f2 será proporcional ao deslocamento dx, que
21

100. pode ser medido com uma resolução da ordem de 0,16 µm ao longo de 60 m com
uma incerteza de ± 1 µm/m sob condições ideais. O valor de f1 não é alterado por
pequenos deslocamentos transversais e inclinações do retrorefletor.
Alguns sistemas mais modernos alcançam uma resolução de 0,01 µm.
Na figura 5.25 está esquematizado o interferômetro linear de espelho plano. Aqui
também um dos raios não altera o caminho óptico em relação ao interferômetro (f2),
ficando o sinal resultante dependente da variação sofrida pelo outro (f1). Com o duplo
percurso do raio entre interferômetro e refletor (espelho plano) a diferença do caminho
óptico com um deslocamento dx será dupla em relação ao interferômetro linear,
duplicando consequentemente a sensibilidade. O refletor, sendo um espelho plano,
poderá ser deslocado, transversalmente, sem influenciar o valor medido.
Figura 5.25: Interferômetros para medição de deslocamentos lineares.
Figura 5.26: Interferômetro angular.
22

101. Na figura 5.26 mostra-se a viabilidade da medição de pequenos deslocamentos
angulares, fazendo-se um arranjo especial de componentes ópticos.
5.6 NORMAS RELATIVAS AOS MEDIDORES DE DESLOCAMENTO
NBR 6388 "Relógios Comparadores com leitura de 0,01 mm".
NBR 10125 "Relógios Comparadores com leitura de 0,001 mm".
DIN 878 "Messuhren"
DIN 879, Teil 1 "Fõnzeiger mit mechanischer Anzeige"
JIS B7536 "Eletrical Comparators"
ISO/R463 "Metric dial gauges for linear measurement"
ASME/ANSI B89.1.10M "Dial Indicators ( For Linear Measurements )"
JIS B 7503 "Dial Gauges Reading in 0,01 mm"
23

102. Capítulo 6
INSTRUMENTOS AUXILIARES DE MEDIÇÃO
6.1 MATERIALIZAÇÃO DE FORMAS GEOMÉTRICAS SIMPLES
Para muitas medições, ou para traçagem de peças, necessita-se de um plano ou
de uma reta de referência materializados.
Partindo deste plano ou reta, considerados perfeitos para o caso em questão
(ou levadas em conta as imperfeições porventura existentes ) pode-se determinar diversas
medidas e estabelecer correlações entre as mesmas: se, por exemplo, numa carcaça com
vários furos deve-se determinar a posição dos eixos destes furos entre si e em relação a
uma superfície de saída ( de referência ) sobre a carcaça, é mais conveniente montá-la
num plano de medição ( placa de traçagem, desempeno ) e determinar todas as medidas
necessárias a partir da mesma com auxílio, por exemplo, de blocos padrão, graminho ou
medidor de coordenadas ( figura 6.1).
Para a traçagem vale o mesmo. Precisa-se então, para tais procedimentos,
desempeno, réguas e esquadros.
Figura 6.1: Exemplo de peça de grande porte medida em desempeno.
6.2 DESEMPENOS
Os desempenos ( placas ) são geralmente de ferro fundido, sem falhas de
fundição, fortemente nervuradas na parte inferior a fim de se ter uma boa rigidez. São
apoiados em três pés com o que se tem sempre um apoio bem definido ( isostático ), e
dispondo-os de modo a conseguir a mínima flecha de flexão pelo peso próprio.
De acordo com a classe de exatidão, a superfície ( plana ) do desempeno pode
1

103. ser usinada ( usinagem de acabamento ), plainada ou rasqueteada, porém nunca
retificadas (pequenas partículas dos grãos de rebolo poderiam ficar presas dentro de
poros do ferro fundido e provocar desgaste demasiado dos instrumentos de medição).
Dimensões e erros admissíveis são normalizados pela DIN 876 e NBR 7263. O
erros admissíveis de planeza, relativos a um plano ideal médio da placa em questão,
podem ser apreciados, na tabela a seguir.
ERROS ADMISSÍVEIS DE DESEMPENOS DIN 876 / NBR 7263
Classe de erro Tolerância de planicidade
00 4 + a/500
0 4 + a/250
1 10 + a/100
2 20 + a/50
3 40 + a/25
a = comprimento do lado maior do desempeno
A verificação da planeza de uma placa é feita com auxílio de uma régua ( de
pequeno erro máximo ), montada sobre dois blocos padrão do mesmo tamanho, como
mostra figura 6.3. A distância entre a régua e a placa é medida em vários pontos com
blocos padrão. As diferenças de medidas destes blocos indicam os erros de planeza da
placa nos pontos correspondentes.
NOTA: Este procedimento, usado na prática pela sua simplicidade, substitui na realidade,
o método baseado na medição da retilineidade em várias direções. Trata-se, pois,
apenas de um método onde a planeza é medida de forma aproximada.
O método de medição do erro da planeza apresentado é o mais elementar.
Muitos outros métodos são empregados e utilizam instrumentação sofisticada como: nível
eletrônico, autocolimador, laser de alinhamento, etc.
Quando se utilizam níveis eletrônicos o procedimento também se baseia na
medição de retilineidade em várias direções, e por processamento dos dados em
software específico, é feito a " amarração " dos dados e se determina o erro de planeza
do desempeno. A vantagem de se utilizar níveis eletrônicos está associada a baixa
incerteza de medição e ao tempo dedicado a calibração, que em geral é menor
comparativamente ao que utiliza réguas padrão.
Se o desempeno é utilizado como plano de referência, ele é disposto na
horizontal, com os pés para baixo e a superfície de medição nivelada com um nível de
bolha, sendo montado em altura conveniente ao trabalho em pé (1000 a 1200 mm)
sobre uma estrutura rígida metálica ( tubular ou de perfis laminados ). Para os trabalhos
nos desempenos, dispõe-se de uma série de acessórios ( figuras 6.1 e 6.2).
2

104. Figura 6.2: Acessórios para trabalhos de medição em desempenos.
Figura 6.3: Controle da planicidade de um desempeno, realizado com régua padrão
e blocos padrão.
Como o nome "desempeno" já indica, ele não é usado apenas para a medição
mas, também, para desempenar superfícies. Entende-se aqui a operação de esfregar o
desempeno, sobre o qual foi aplicada tinta ( pastosa, a base de óleo geralmente de cor
azul escura ) finamente distribuída, sobre a superfície a desempenar, com o objetivo de
tornar bem visíveis ( "pintar" ) os pontos altos desta superfície. Os pontos " pintados " são
removidos em seguida, pelo rasqueteamento. Repetindo o processo descrito várias vezes,
consegue-se uma superfície com planeza próxima daquela do desempeno. Neste
processo, obviamente o desempeno é usado em várias posições ( também de cabeça
3

105. para baixo ), de acordo com a posição da superfície a desempenar, e é manobrado por
intermédio de maçanetas adequadas.
O procedimento descrito trata-se de uma comparação entre a superfície a
controlar e a do desempeno, comparação que não merece inteira confiança, já que os
dois corpos se compensam de um certo modo e, além disso, o erro de comparação
depende também da espessura da camada de tinta ( se for muita espessa, "pinta-se"
também lugares mais baixos da superfície a desempenar ).
Placas menores ( até cerca de 200 mm de diâmetro ) são fabricadas de aço,
temperadas e retificadas. Os erros em sua planeza são da ordem de ± 0,02 mm.
Desempenos de referência para traçagem e medição são fabricados atualmente
em granito. O granito, como passa por " envelhecimento natural " que ocorre após vários
milhões de anos, não tende a deformar-se com o tempo ( como é o caso, por exemplo,
do ferro fundido ). Além disso, essas placas de granito, são construídas de tal maneira
que, ao serem danificadas por algum impacto ( por exemplo, queda por descuido de
alguma peça a ser medida) soltam lascas bem visíveis no local do impacto, perdendo a
sua planeza apenas parcialmente. Possuem a desvantagem de não permitirem o uso de
suportes magnéticos.
6.3 RÉGUAS
Para a representação de eixos de referência e de linhas retas ( bordos de
referência ), em muitos casos são empregados as réguas, construídas de aço, ferro
fundido ou granito.
Uma secção retangular ou de perfil em I ( réguas de oficina ) é a mais freqüente,
mas para os casos especiais, usam-se também outras seções: com gume ( régua de fio ),
com seção triangular ou de quatro cantos ( réguas de desempeno ) e outras ( figuras
6.4).
Correspondendo às suas múltiplas aplicações, fabricam-se em comprimentos de
até 5 metros ( em casos especiais também maiores ) e com erros admissíveis
normalizados pela DIN 874 como se pode ver na tabela a seguir:
ERROS ADMISSÍVEIS DE RÉGUAS ( DIN 874 )
Classe de Erro Erro Máximo Permitido
de Planicidade (µm)
00 1 + L /150
0 2 + L /100
I 4 + L /60
II 8 + L /40
L = Comprimento da régua em mm.
4

106. A régua de fio não tem uma superfície de medição, mas apenas um bordo de
medição ( figura 6.4.a ). Ela é, por isto, muito apropriada para o controle de planeza
pelo processo da fresta luminosa. Com ela pode-se perceber frestas de até 0,001 mm
que aparecem "ampliadas " em virtude da refração da luz no bordo da régua.
Figura 6.4: Réguas.
As superfícies de medição das réguas com seção retangular são os lados estreitos
do retângulo ( figura 6.4.b ).
Réguas padrão acima de 2 metros e réguas de oficina de qualidade I acima de
2,5 m de comprimento são rebaixadas nas faces laterais de forma que resulta uma
secção I ( figura 6.4.c). Os lados estreitos da seção são as superfícies de medição que
devem satisfazer aos erros máximos anteriormente citados.
As réguas de 3 e 4 cantos ( figura 6.4.d e 6.4.e) têm os respectivos bordos de
medição temperados.
Na figura 6.5 tem-se uma régua de desempeno, usada para desempenar
superfícies estreitas porém compridas com nervuras de reforço em formas parabólicas, e é
fabricada com a mesma classe de erro das placas de desempenar.
5

107. Figura 6.5: Régua de desempeno.
No caso da régua apoiar-se em dois pontos, a deflexão mínima ocorre quando
estes pontos de apoio estão afastados dos extremos de um valor igual a 0,22315. L
( onde L é o comprimento da régua ) segundo figura 6.9. A flexão pelo peso próprio, que
representa um erro adicional, não precisa ser levada em consideração com este tipo de
apoio. Para trabalhos criteriosos, no entanto, deve-se considerar a flexão sempre que se é
forçado a escolher outro tipo de apoio como, por exemplo, nos extremos da régua.
Figura 6.6: Método dos três cantos para determinação da retilineidade.
A verificação da planeza das superfícies de medição pode ser feita de maneira
semelhante à da figura 6.3, usando-se um plano ou uma régua de elevada qualidade,
cujos erros da planeza são conhecidos. Quando não se dispões de tal recurso, pode-se
resolver o problema pelo método chamado de " Medição de três cantos ", figura 6.6. A
régua R a ser calibrada ( figura 6.6.a) é colocada sobre dois apoios de mesma altura S
num plano P ( ou régua ) de referência, cujos erros de planeza são também
desconhecidos. Em vários pontos 1,2, ..., distribuídos ao longo do comprimento L podem
ser obtidas as medidas MAC, como mostra esquematicamente e em escala aumentada a
6

108. figura 6.6.b. As superfícies A e C da régua a calibrar e a de referência possuem erros de
planeza ( desconhecidos ) a e c, respectivamente. Para cada um dos pontos 1,2, ...., tem-
se pois a equação:
MAC + 1AC = S, sendo 1AC = a + c.
Coloca-se em seguida a régua a ser verificada sobre os mesmos apoios, porém
com a superfície B virada para baixo, para o lado da placa P ( figura 6.6.c ). Nos
mesmos pontos 1,2, ..., são medidos os valores MBC, e tem-se:
MBC + 1BC = S sendo 1BC = b + c
onde b e c são os erros de planeza ( desconhecidos ) das superfícies B e C,
respectivamente.
Finalmente, mede-se a largura da régua R dos locais dos pontos 1, 2....,
obtendo-se as medidas MAB ( figura 6.6.d ). Como mostra a figura 6.6.e, tem-se:
MAB - 1AB = d onde 1AB = a + b
onde d é a largura da régua R nos pontos de apoio ( escolhidos de modo que ambos
forneçam obrigatoriamente o mesmo "d" ).
Do modo descrito obtém-se, para cada um dos pontos 1,2, .... três equações com
três incógnitas ( erros de planeza a, b, c das superfícies A, B, C, respectivamente ) que
podem ser a partir daí determinadas.
Deve-se ressaltar que o resultado para cada um dos pontos pode ter bastante
erro, já que se torna necessário levar em consideração os erros possíveis de cada uma
das etapas acima descritas. Se as medições de MAC têm as dispersões DMAC = ± 2 µm,
DMBC = ± 2 µm e DMAB = ± 3 µm, respectivamente, a incerteza do resultado final é
DM = ± ( DM AC )2 + ( DM BC )2 + (DM AB )2 = 17 = ±4 µm
A retilineidade ( neste caso igual a planeza) de uma régua pode ser estabelecida,
também, com nível de bolha, um autocolimador, ou ainda, por intermédio de um laser de
alinhamento.
6.4 ESQUADROS
Esquadros possuem ângulos retos que são utilizados na medição ou traçagem de
planos e/ou retas perpendiculares.
As formas mais comuns estão mostradas na figura 6.7. Outras formas de
7

109. esquadros estão mostradas na figura 6.8.a ( esquadro de coluna ) e 6.8.b ( esquadro de
coluna cilíndrica ).
Figura 6.7: Esquadros.
Os erros admissíveis dos esquadros comuns são normalizados pela DIN 875. Os
erros permitidos no perpendicularismo da superfície de medição dos esquadros, segundo
a norma citada, podem ser vistos na tabela apresentada a seguir e na figura 6.7.
ERROS ADMISSÍVEIS DE ESQUADROS ( DIN 875 )
Grau de Erro de Perpendicularidade em
Precisão (mm), sendo L em (mm)
00 ± ( 0,002 + L /100.000 )
0 ± ( 0,005 + L /50.000 )
1 ± ( 0,010 + L /20.000 )
2 ± ( 0,020 + L /10.000 )
O conceito " erro de perpendicularidade " está esclarecido na figura 6.9: é o
afastamento d da aresta do esquadro, a partir de uma linha vertical V ideal, medido na
altura L, sendo o sinal positivo (+) quando o ângulo verdadeiro do esquadro for maior do
que 90° , e negativo (-) no caso oposto. Assim, o erro de perpendicularidade é dado em
micrometros por determinado comprimento L, e é válido para a superfície de medição (m
na figura 6.9). Para os lados a e b, os erros permitidos de perpendicularidade são o triplo
do valor permitido para a superfície de medição que consta na tabela.
8

110. Figura 6.8: Esquadros de coluna .
Figura 6.9: Erro de perpendicularismo em esquadros.
esquadros.
A verificação da perpendicularidade é conduzida com auxílio de um esquadro de
referência de tamanho adequado, cujos erros de perpendicularidade são conhecidos, e
de blocos-padrão, precedendo-se da maneira descrita a seguir (figura 6.10.a).
9

111. Figura 6.10: Verificação do perpendicularismo.
O esquadro E1 a ser verificado e o esquadro E2 apoiam-se sobre um desempeno
com um bloco padrão de comprimento e1 conhecido, entre os mesmos. Em certa altura L
mede-se por intermédio de uma composição de blocos padrão, a distância verdadeira e2
entre as superfícies de medição m1 e m2 dos esquadros E1 e E2, respectivamente. Se
não houver erro de perpendicularidade, e1 = e2. Se houver erros, tem-se:
e2 = e1 + a +b
onde a ( desconhecido ), b ( conhecido ) são os erros de perpendicularidade dos
esquadros E1, E2, respectivamente. Torna-se, pois, fácil calcular o desvio a:
a = e2 – e1 –b
Se, por outro lado, os erros de perpendicularidade do esquadro de referência não forem
conhecidos, torna-se necessário complementar a medição descrita anteriormente por
mais uma representada na figura 6.10.b. O esquadro E1 a ser verificado, é colocado
lado a lado com o de referência E2 e, usando o bloco padrão e3 de comprimento
conhecido mais a régua de fio F medem-se, por intermédio de uma composição de
blocos-padrão e4, a diferença dos erros reais de perpendicularidade na altura L. Três
casos são possíveis:
a) Sabemos que o esquadro de referência tem incerteza de medição menor ou
igual a um décimo da n certeza de medição do esquadro a calibrar
( IMpadrão ≤ IMcalibrar /10 ) e por isso supusemos que os erros de perpendicularidade do
mesmo podem ser desprezados. Neste caso, obtém-se diretamente na medição, de
acordo com a figura 6.10.a, o erro de perpendicularidade procurado que se verifica
10

112. através da medição de acordo com a figura 6.10.b.
b) Os erros de perpendicularidade do esquadro de referência E2 são menores do que
aqueles do esquadro E1. O erro de perpendicularidade a, na altura L, neste caso é:
( e2 − e1 ) + ( e4 − e3 )
a=
2
obtendo-se a diferença e2 – e1 =a + b da medição segundo a figura 6.10.a e a
diferença e4 – e3 =a - b da medição de acordo com a figura 6.10.b. Ao eliminar b ( ora
desconhecido ) das duas equações, obtém-se a fórmula acima citada.
c) Os erros de perpendicularidade do esquadro E2 de referência, são maiores do que o
do esquadro E1 a ser verificado. O erro procurado neste caso é
( e2 − e1 ) − (e 4 − e3 )
a=
2
NOTA: O uso de blocos padrão e1 e e3, nas medições, de acordo com as figuras 6.10.a
e 6.10.b, respectivamente, deve-se a motivos práticos. Se encostarmos os esquadros e a
régua de fio diretamente seria difícil medir a fresta estreita surgida, já que os erros são,
comumente pequenos.
NORMAS: DIN 875/81 Stahlwinkel 90º
NBR 9972/87 Esquadros 90º
11

113. Capítulo 7
CALIBRADORES
7.1 INTRODUÇÃO
Calibradores são padrões geométricos corporificados largamente empregadas na
indústria metal-mecânica. Na fabricação de peças sujeitas a ajuste, as respectivas
dimensões têm tolerâncias de fabricação fixadas pelo projeto. Para se efetuar a
qualificação destas peças de forma rápida utilizam-se os calibradores do tipo
passa/não-passa.
Dada a sua grande simplicidade e seu preço relativamente reduzido, os
calibradores constituem uma solução econômica para uma série de problemas de
medição na indústria, como verificação de furos, eixos, roscas, etc., quanto a seu
enquadramento ou não na faixa de tolerância.
Com a introdução da automatização, os calibradores no entanto, vão perdendo a
sua importância dentro do processo de fabricação.
7.2 CARACTERÍSTICAS DE FABRICAÇÃO
Os calibradores são fabricados de tal forma a possuírem as dimensões máximas e
mínimas de uma determinada geometria, como furos, roscas, comprimentos, etc.
A fabricação de calibradores exige uma técnica apurada visto que suas tolerâncias
não devem exceder de um quinto a um décimo das tolerâncias da dimensão a verificar.
Calibradores de roscas, por exemplo, apresentam tolerâncias de fabricação que partem
da ordem de ± 4 µm. Para realizar a calibração destes padrões é necessário, portanto ,
padrões com baixa incerteza de medição.
A resistência à abrasão dos calibradores é um requisito importante devido ao seu
constante contato com as peças. Os calibradores são fabricados com aço endurecido
por cementação, ou revestido de cromo duro, carboneto de tungstênio, etc.
7.3 TIPOS E APLICAÇÕES
Existem basicamente dois grupos de calibradores: fixos e ajustáveis ( figura 7.1 ).
Os primeiros são exclusivamente empregados para a verificação de apenas uma
determinada dimensão, o que implica em dispor-se de um número elevado de
calibradores para atender às diversas medidas nominais com suas respectivas tolerâncias
de fabricação. Os calibradores tipo tampão e anel se enquadram neste grupo.
1

114. Para minimizar custos e tempo no controle, surgiram os calibradores ajustáveis que
permitem a verificação de uma faixa de dimensões ( figura 7.1.b ).
Figura 7.1: Calibradores fixos e ajustáveis.
7.4 CALIBRADORES FIXOS
7.4.1 Calibradores Tampões
Os calibradores tampões são utilizados para a verificação da dimensão de furos.
Eles apresentam dois lados: um Passa e outro Não-Passa ( figura 7.2 ).
Figura 7.2: Calibradores tampões.
Calibradores passa-não-passa são constituídos obedecendo o princípio de Taylor
( Figura 7.9 ) . Este princípio diz: no lado bom deve-se ensaiar o "casamento". Assim,
por exemplo, o lado " bom " do calibrador para furos tem a forma de um eixo e tem de
encaixar no furo. Com o lado " ruim " do calibrador deve-se testar se em nenhuma
posição a dimensão especificada é ultrapassada. Para o calibrador de furos o lado "
2

115. refugo " possui duas superfícies de contato pontuais. O calibrador não deve em nenhuma
posição encaixar no furo.
Para os calibradores existe um sistema de tolerância especial ( Figura 7.10 ).
Como pode ser observado, as tolerâncias de fabricação são bastante mais estreitas
e deve-se prever o próprio desgaste no lado passa. Maiores detalhes podem ser
observados nas normas DIN 7162 A 7164, por exemplo.
Figura 7.3: Calibrador de altura digital.
7.4.2 Calibradores Anulares
Os calibradores anulares são utilizados para a verificação de diâmetros externos,
como eixos. Na figura 7.11 apresentam-se os diferentes tipos de calibração anulares.
7.4.3 Calibradores de Boca e Calibradores Planos
Estes calibradores ( figura 7.12 ), que frequentemente substituem os anulares e
tampões, somente ficam em contato com a peça a medir numa pequena região,
ocorrendo contato localizado ou mesmo em duas linhas opostas ( contato linear ).
3

116. Figura 7.4: Calibrador de profundidade.
Figura 7.5: Calibradores fixos: pente de rosca métrica.
4

117. Figura 7.6: Calibradores de folga.
Figura 7.7: Calibradores fixos: fieiras.
5

118. Figura 7.8: Calibradores para furos e rasgos.
Figura 7.9: Calibradores (Princípio de Taylor).
O calibrador de boca tem superfícies de contato planas e paralelas que permitem
controlar peças cilíndricas e prismas com faces paralelas ( figura 7.12.a ). Na figura
7.1.b é mostrado um calibrador de boca ajustável.
O calibrador plano tem superfícies de contato cilíndricas que permitem, como o
tampão, verificar um furo ( figura 7.12. b ).
6

119. Figura 7.10: Tolerância para calibradores
DIN 7162 a DIN 7164.
Figura 7.11: Calibradores anulares.
7.4.4 Calibradores tipo Haste
Tem as superfícies de medição em forma esférica ou plana ( figura 7.13 ). São
utilizados para verificação de furos, em geral acima de 100 mm, ou distâncias entre
superfícies paralelas, por exemplo na calibração ou ajustes de micrômetros.
Para verificação de furos são fabricados aos pares: um com a dimensão máxima e
outro com a mínima da peça. Devem ocupar na peça uma posição que define
geometricamente o elemento a controlar. Assim o calibrador haste para furos deve ser
situado numa posição perpendicular a duas geratrizes opostas, a fim de confundir-se
com um diâmetro.
7

120. Figura 7.12: Calibradores de boca e calibradores planos.
Figura 7.13: Calibradores tipo haste.
7.4.5 Calibradores de Roscas Cilíndricas
Na figura 7.2 e é mostrado um calibrador tampão de rosca cilíndrica. É
antieconômico medir todos os parâmetros de uma rosca no controle de peças. Em vez
disso, recorre-se ao emprego de calibradores de roscas que proporcionam uma
verificação simultânea de todos os parâmetros da rosca.
O lado passa tem uma rosca com o perfil completo e deve ser enroscado
facilmente. O lado não passa é mais curto e possui de 2 a 3 filetes cujos flancos estão
8

121. rebaixados na parte dos diâmetros externos e do núcleo. O mesmo não deve poder ser
roscado.
O diâmetro liso, do lado não passa do calibrador, serve para verificar o diâmetro
do núcleo da rosca interna. Na figura 7.11.a é mostrado um calibrador cilíndrico
anular.
As tolerâncias de fabricação de calibradores de rosca cilíndricos são dadas pelas
normas ABNT NBR 8225, DIN 13, DIN 259, ISO 228/I, ANSI B1.1 , entre outras.
7.4.6 Calibradores de Roscas Cônicas
Estes tipos de calibradores seguem as formas e dimensões padronizadas por
normas como BS 21 e USAS B2.1. São utilizados para verificar roscas a serem abertas
em tubos, registros, bujões, válvulas e conexões, abrangendo as roscas destinadas a
formar juntas estanques:
- rosca externa cônica
- rosca interna cônica
- rosca interna cilíndrica
Existem 2 sistemas de calibradores e considera-se que, em condições apropriadas,
a calibração por qualquer dos dois sistemas recomendados, acompanhada por inspeção
visual, será suficiente para garantir produtos satisfatórios, com os quais se farão juntas
perfeitas.
O sistema "A" é indicado para uso onde métodos de controle de produção são
empregados para garantir a elevada qualidade da rosca, enquanto o sistema " B " é
indicado para uso onde um controle adequado da produção não foi estabelecido.
a) Sistema A
Compreende os seguintes tipos de calibradores:
- Calibrador tampão cônico com rosca completa
Este calibrador tem um entalhe no plano de calibração e o comprimento da rosca
do entalhe no plano de calibração até a extremidade menor do tampão, é igual
ao comprimento básico de calibração ( figura 7.14.b).
- Calibrador anular com rosca cônica
Este calibrador tem um comprimento de rosca igual ao comprimento básico de
calibração, e os diâmetros na extremidade maior são iguais aos diâmetros básicos
no plano de calibração ( figura 7.14.a ).
9

122. Figura 7.14: Calibração de roscas cônicas: sistema A.
b) Sistema B
Compreende os seguintes calibradores:
- Calibrador tampão cônico com rosca completa
Tem um comprimento total de rosca igual ao comprimento da rosca útil para
comprimento máximo de calibração e possui um entalhe igual à tolerância total na
posição do plano de calibração.
A face superior do entalhe é marcada positiva (+) e a face inferior, é marcada
negativa (-) ( figura 7.15.b ), devendo o limite da rosca situar-se entre estas faces
quando aplicado o calibrador.
- Calibrador anular com rosca cônica completa
Este calibrador tem um comprimento total de rosca igual ao comprimento da rosca
útil para comprimento máximo de calibração menos a metade do comprimento
para aperto com chave, e um entalhe igual à tolerância total do comprimento de
calibração. A face superior do entalhe é marcada positiva (+) e a face inferior é
marcada negativa (-) ( figura 7.15.a ).
10

123. Figura 7.15: Calibração de roscas cônicas: sistema B.
7.5 QUALIFICAÇÃO DE CALIBRADORES
As condições em que é executado o controle de qualidade utilizando-se
calibradores, traz consigo um desgaste relativamente rápido dos mesmos devido ao
atrito
existente entre o calibrador e a peça a ser controlada. É por conseguinte importante
periodicamente realizar a calibração dos calibradores, que consiste em determinar as
dimensões efetivas dos mesmos para comparação com os valores normalizados.
Aos valores das dimensões nominais dos calibradores são também atribuídas
tolerâncias, de sorte que sempre teremos um dos casos:
- peças boas sendo refugadas
- peças que deveriam ser refugadas e são consideradas boas.
Algumas normas sobre calibradores são relacionadas abaixo:
Tampões................................. DIN 2245
Anéis...................................... DIN 2250
De boca Progressivo.................. DIN 273
De boca Passa......................... DIN 2232
De boca Não Passa.................. DIN 2233
De boca.................................. DIN 2234
De boca.................................. DIN 2235
De boca.................................. DIN 2238
11

124. De rosca cilíndrica.................... NBR 5876,6159,6160 e 6161,DIN13 e 159,ANSI B1.1
De rosca cônica....................... NBR 8018, USAS 2.1, BS 2.1 DIN 2999
Elas apresentam as tolerâncias de fabricação e de desgaste para os diferentes
calibradores.
12

125. Capítulo 8
MÁQUINAS DE MEDIR
8.1 INTRUDUÇÃO
Máquina de medir é o nome corrente para sistemas de medição geométrico de porte
razoável e que se assemelham às máquinas-ferramenta no que se refere à estrutura.
As máquinas de medir, na sua concepção tradicional, estão perdendo importância pelo
fato:
- de serem de aplicação dirigida, pois foram concebidas especialmente para medir
certos grupos de peças;
- das máquinas de medir por coordenadas, totalmente universais em suas aplicações,
assumirem com vantagens os trabalhos realizados pelas máquinas dedicadas;
- de representarem um elevado investimento financeiro.
A seguir apresentam-se alguns detalhes relativos a alguns tipos construtivos de
máquinas de medir.
Figura 8.1: Máquina de medir comprimentos (segundo Abbé).
8.2 MÁQUINA ABBÉ
Assim denominada pelo fato de atender plenamente o princípio operacional
formulado por Ernst Abbé, isto é, a escala que constitui o padrão de comprimento está
alinhada à dimensão a controlar no objeto a medir (figura 8.1). Desta forma as causas
de erros ficam restritas à medição na escala, influências térmicas e da força de
medição. As máquinas tradicionais utilizam escalas ópticas graduadas, enquanto que as
mais modernas servem-se de escalas eletro-ópticas, o que favorece a automatização da
1

126. medição (figura 8.2). A incerteza de medição para comprimentos é da ordem de
±(0,5+L/1000 ) µm.
Estas máquinas encontram grande aplicações nos laboratórios de metrolologia, em
trabalhos como calibração de calibradores e medição de peças em geral.
Figura 8.2: Automatização da medição em uma máquina Abbé-digital.
8.3 MICROSCÓPIOS DE MEDIÇÃO
Assim denominado em função de utilizar um sistema óptico idêntico ao de um
microscópio, para localizar ponto (aresta) de medição sobre a peça que está sendo
medida.
Estes sistemas de medição destinam-se, principalmente para peças pequenas e dispõe
de medidores de deslocamentos linear e angular. Uma aplicação bastante rotineira para
microscópio é a medição de ângulos de rosca de peças em geral, inclusive de
calibradores de rosca. Para facilitar a interpretação da imagem e a medição por sobre a
mesma, os microscópios possuem junto à sua ocular uma máscara com os perfis de
rosca normalizados (figura 8.3).
Figura 8.3: Oculares para microscópios de medição.
2

127. Os microscópios, assim como os projetores de perfil podem operar pelos métodos de
projeção episcópica e diascópica, conforme estejam a fonte de luz e imagem projetada
do mesmo lado ou em lados opostos em relação à peça, respectivamente.
8.4 PROJETORES DE PERFIL
O problema de medição de peças pequenas reside, muitas vezes, no acaso do
instrumento de medir até o ponto desejado. Uma forma de solucionar o problema é
medir sobre ou com auxílio de uma imagem ampliada (figura 8.4). existem duas formas:
- medição na imagem ampliada
- medição na peça, posicionada via imagem ampliada.
No segundo método, distorções da imagem não irão gerar erros.
Figura 8.4: Métodos básicos de medição com um projetor de perfis.
Os projetores de perfil podem operar com diferentes graus de ampliação da imagem
(figura 8.5), sendo comumente adotados os fatores 10x, 20x e 50x. As principais fontes
de erro nos projetores de perfil são: ampliação, posicionamento da mesa/feixe luminoso.
Retilineidade e ortogonalidade dos movimentos.
8.5 MÁQUINAS DEDICADAS
Para facilitar a medição de determinadas peças de geometria complexa, foram
desenvolvidas ao longo de muitos anos, algumas máquinas especiais, de forma que o
processo de medição simplifica-se grandemente, evitando a realização de intensivos e
complexos cálculos. Dentre estas máquinas destacam-se:
3

128. a) Máquina de medir cames
São máquinas previstas para medições em coordenadas polares, onde angulares são
obtidas em um cabeçote divisor e a posição linear por um computador óptico ou
mecânico (figura 8.6). Além de cames, são adequadas ainda para a medição de
rodas dentadas e eixos ranhurados.
b) Máquina de medir engrenagens
Sua forma construtiva e princípios de medição permitem obter grandezas como: perfil
da envolvente, inclinação da hélice, diâmetros, passo, espessura de dente,
concentricidade, e outros. Atualmente, com a associação de comando numérico e
computador, foi ampliada ainda mais o potencial destas máquinas.
Figura 8.5: Projetor de perfil (segundo Mitutoyo).
8.6 MESAS DIVISORAS
Como medidor de ângulos, aplicando o método absoluto ou diferencial, pode-se
utilizar com uma série de vantagens operacionais uma mesa divisora semelhante à
utilizada em máquinas ferramentas, que no entanto, deverá apresentar melhores
características de desempenho metrológico.
4

129. Figura 8.6: Máquina de medir cames.
5

130. Capítulo 9
MÁQUINAS DE MEDIR POR COORDENADAS
9.1 IMPORTÂNCIA
Ao longo de alguns anos ocorreu intensivo desenvolvimento tecnológico nos
processos de usinagem das peças, destacando-se o surgimento dos centros de usinagem
com comando numérico. Paralelamente, refinaram-se as exigências quanto à
conformidade geométrica dos componentes de sistemas mecânicos resultando em
especificações mais severas de projeto, de modo a garantir um elevado desempenho
funcional dos mesmos. Pelo não desenvolvimento da tecnologia de medição no mesmo
ritmo, criou-se uma defasagem tecnológica a tal ponto, que o controle de certas peças
tornava-se extremamente difícil e economicamente inviável.
A aplicação racional da tecnologia de medição por coordenadas tornou-se viável
com o desenvolvimento dos computadores que passaram a ter:
- enormes potencialidades matemáticas;
- flexibilidade de comunicação e conexão com um processo;
- resistência a ambientes industriais;
- pequeno porte e baixo custo.
Através de uma máquina de medir por coordenadas (figura 9.1) determina-se, de
forma universal, com um mínimo de dispositivos e instrumentos específicos, as
coordenadas de certos pontos sobre a peças a controlar. Tais pontos convenientemente
processados pelo computador associado, resultam os parâmetros geométricos da peça.
O desenvolvimento das máquinas de medir por coordenadas (MMC) foi
favorecido ainda pela evolução dos sistemas de medição de deslocamento eletrônicos,
que permitem elevar a sua qualidade e viabilizaram a sua integração com sistemas
automatizados de fabricação. As MMC's têm em comum com tais sistemas a característica
de grande flexibilidade.
9.2 MEDIÇÃO POR COORDENADAS
Com base nos sistemas de medição de deslocamento das máquinas de medir por
coordenadas, é possível conhecer a posição que um elemento localizador ocupa dentro
do espaço de trabalho da máquina (figura 9.2). Este localizador, operando por princípios
eletro-mecânico e articulado, é chamado de apalpador. Esclarecendo de modo grosseiro,
1

131. ele relaciona o ponto de contato do seu sensor com a peça a um ponto de referência
conhecido dentro do sistema coordenado.
Figura 9.1: Máquina de medir coordenadas (tridimensional).
A determinação das coordenadas dos pontos sobre a peça serve de base
para a determinação dos parâmetros de elementos geométricos (dimensão, forma e
posição) como por exemplo a distância entre superfícies, o diâmetro e a posição de um
círculo, e outros.
Para determinar o comprimento de um bloco prismático, é suficiente conhecer as
coordenadas dos pontos sobre as faces extremas. O cálculo do comprimento é bastante
simples se o bloco estiver posicionado paralelamente a um dos eixos coordenados,
tornando-se mais trabalhosa a obtenção do resultado caso a posição do bloco seja
aleatória no espaço. Para determinar o diâmetro de um círculo, basta conhecer as
coordenadas de três pontos deste círculo. A operação de cálculo relativa a uma posição
espacial qualquer é bem mais complexa do que aquela para o círculo contido em plano
paralelo a um dos planos definidos por dois eixos coordenado. Nos dois casos, uma
solução rápida, precisa e confiável só é possível com o emprego de um computador/
calculadora para efetuar o processamento.
A figura 9.3 mostra recursos básicos de processamento geométrico usualmente
encontrados em sistemas computadorizados. Esta figura mostra também que os cálculos,
em geral, não se baseiam exatamente nos pontos de contato do sensor com a peça, mas
sim nas posições dos centros do sensor após o contato, e na compensação do seu raio
conforme condições específicas de cada tipo de elemento medido.
2

132. Figura 9.2: Medição de coordenadas: exemplo de medição.
Figura 9.3: Determinação de elementos geométricos por coordenada.
3

133. Figura 9.4: Formas construtivas de máquinas de medir por coordenada.
9.3 CONFIGURAÇÕES MECÂNICAS
Os cálculos de comprimentos, distâncias entre eixos, diâmetros, ângulos, desvios
de planicidade e todos os outros parâmetros geométricos, são feitos a partir das
coordenadas de pontos medidos em relação a um sistema coordenado definido pela
máquina de medir. Para constituir uma máquina universal de medir, é suficiente capacitá-
la a operarem três coordenadas lineares ortogonais. No entanto, a eficiência é
aumentada significativamente, se houver à disposição o recurso do movimento angular
em um dos planos coordenados, especialmente tratando-se de peças simétricas de
rotação, como engrenagens, discos de cames, etc. (figura 9.2). A figura 9.4 mostra
algumas formas construtivas de máquinas de medir. A forma construtiva esta muito
relacionada com o volume de medição, com a área de acesso para a peça, com a
incerteza de medição e algumas vezes com a própria tecnologia acumulada por um
certo fabricante.
Os fabricantes em geral equipam suas máquinas com mancais pneumáticos, embora
sejam encontradas algumas máquinas guarnecidas com guias de roletes ou esferas
recirculantes. Os mancais pneumáticos permitem um movimento com mínimo de atrito,
favorecendo alcançar elevado nível de precisão para a MMC. Quanto aos medidores de
deslocamento (posição), tem-se o uso generalizado de escalas eletro-ópticas
incrementais, operando com resoluções de 0,1 a 2 µm.
9.4 APALPADORES
O localizador também é de vital importância na determinação das coordenadas
dos pontos, podendo operar com ou sem contato com a peça a medir (figura 9.5). Os
sem contato são posicionados manualmente e identificam o ponto com base num sistema
óptico de projetor de perfil ou microscópio com cruz reticulada, não sendo próprios para
aplicações universais e automatizadas (figura 9.5b). Tais sistemas ópticos têm sido
substituídos por câmeras digitais e processamento computadorizado de imagens.
4

134. Figura 9.5: Localizadores.
Figura 9.6: Apalpadores laser para máquinas de medir por coordenadas.
A figura 9.6 mostra localizadores ópticos mais modernos, baseados em um feixe
laser e método de medição por triangulação.
Associados a dispositivos articulados de posicionamento, estes localizadores
permitem medir, sem contato, superfícies com forma irregular.
Os localizadores com contato podem ser rígidos, apresentando diferentes
configurações do sensor (figura 9.5a), em função da característica do ponto a ser
5

135. localizado na peça, ou pode ser articulado (figura 9.5c), sendo a localização do ponto de
medida relacionada à geração de um sinal elétrico.
Figura 9.7: Configurações mecânicas de apalpadores.
Há dois tipos básicos de apalpadores:
- Apalpador medidor - fornece um sinal proporcional ao deslocamento do sensor
após o contato com a peça (figura 9.7); este sinal pode ser usado para o controle de
posicionamento (figura 9.8), para o disparo da leitura ou para obter o valor do
deslocamento,
que adicionado aos valores medidos nas escalas, resulta nas coordenadas do ponto de
medição.
- Apalpador comutador - fornece um sinal de comutação ( liga/desliga ) após um
deslocamento pré-definido do sensor (figura 9.9).
Através de uma calibração inicial do apalpador, com determinado sensor, determina-se o
diâmetro virtual da esfera, que considera o raio e a deflexão para emissão do sinal. As
coordenadas e os parâmetros geométricos do elemento medido são corrigidas com
aquele raio.
6

136. Figura 9.8: Máquina de medir coordenadas (tridimensional).
Figura 9.9: Apalpadores 3D-Comutador (erros do ponto de referência).
Os métodos para obtenção das coordenadas de um ponto no instante de medição são os
seguintes:
7

137. - Método diferencial, que consiste na associação dos valores indicados por um
apalpador medidor com os valores coordenados das escalas da máquina após o contato
com a peça;
- Método absoluto, onde as coordenadas da máquina são adquiridas no instante da
emissão do sinal de comutação de um apalpador comutador ou em uma condição pré-
definida de deflexão de um apalpador medidor.
Observa-se que as medições feitas pelo método diferencial são estáticas, ao passo
que com o método absoluto elas são dinâmicas.
As máquinas de melhor qualidade operam com o apalpador medidor, sendo
adequadas a trabalhos em laboratórios. De outro modo, aquelas que operam com o
apalpador comutador são mais rápidas e se adequam ao controle geométrico com
menores requisitos de precisão, como no controle de qualidade próximo à produção.
9.5 ERROS DE MEDIÇÃO
A qualidade dos resultados de uma MMC é função, em primeiro plano, dos erros
de medição das coordenadas. Portanto, para alcançar bons resultados deve-se garantir
que a máquina tenha movimentos relativos geometricamente bem definidos, com
mínimos erros de retilineidade, ortogonalidade, planicidade, etc (mínima distorção do
sistema coordenado em relação ao ideal). Isto implica em uma estrutura bastante rígida,
de precisão e estável. As fontes de erro em uma máquina de medir coordenadas são
muitas e estão indicadas no quadro na figura 9.10.
O elemento mais crítico do sistema é o localizador, no caso, o apalpador. Segue-
se a estrutura da máquina de medir, que estabelece os movimentos, afetando-os de erros,
isto é, com desvios de retilineidade, ortogonalidade, posicionamento, etc.
Diversos ensaios são necessários para avaliar a incerteza de medição da MMC,
destacando-se aqueles que verificam os erros dos movimentos no espaço e que verificam
o comportamento metrológico do apalpador.
A normalização destes ensaios ainda é objeto de intensos estudos nos países
desenvolvidos. Entre normas e recomendações disponíveis, cita-se:
- ISO 10.360 - Coordinate Metrology - Part 2: Performance Assessment of Coordinate
Measuring Machines (CMMês), 1993
- VDI/VDE 2617 - Accuracy of Coordinate Measuring Machines, Characteristics
and their Checking - April, 1986:
. Part 1 - Generalities
. Part 2 -Uncertainty of measurement specific to the measuring task; length
measurement uncertainty
8

138. . Part 3 - Components of measurement diviation
. Batt 5 - Ueberwachung von Koordinatenmessgeraeten duch Pruefkoerper.
- “CCMMA” Genauigkeitsspezifikation fuer Koordinaten Messgeraete - Divulgação
da CMMA - Coordinate Measuring Machine
Manufacturers Association, 1982.
- ANSI/ASME B89.1.12M/1985 - Methods for Perfamance Evoluation of
Coordinate Measuring Machines;
Figura 9.10: Fontes de erros em uma máquina de medir coordenadas.
Ao final deste capítulo estão anexados alguns resultados de um ensaio geométrico
realizado em um máquina de medir por coordenadas de porte médio.
Uma MMC destinada a serviços de laboratórios metrológicos, com um espaço de
trabalho de 500 x 500 x 500 mm, com escalas eletro-ópticas operando com uma
resolução de 0,1 µm apresenta uma incerteza de medição igual ± (0,5 + L/900) µm. Este
elevado desempenho metrológico é atingido sob condições climáticas controladas,
compensação de erros sistemáticos por software e compensação da dilatação térmica da
peça e das escalas da máquina.
Outros modelos de MMC, destinados propriamente ao controle industrial
apresentam incertezas de medição na faixa de ± 5 a ± 20 µm para comprimentos de
trabalho da ordem de 1 m.
A compensação de erros sistemáticos é realizada pelo computador, a partir dos
resultados de ensaios geométricos realizados pelo fabricante. Um algoritmo próprio
9

139. simula a associação de todas as componentes de erros, determinando o erro que a
máquina comete em cada ponto.
9.6 NÍVEIS DE AUTOMAÇÃO
Figura 9.11: Máquina de medir coordenadas não automatizada.
Algumas configurações de máquinas de medir por coordenadas são apresentadas
a seguir conforme o seu nível de automatização.
a) MMC com acionamento manual. Correspondem às máquinas mais simples com
movimentação manual, leitura e cálculos realizados pelo próprio operador (figura 9.11).
Atualmente é uma configuração apenas didática, pois na prática não se pode mais
admitir uma MMC sem computador.
b) MMC com acionamento manual e com computador. A associação do computador
permite realizar trabalhos de medição complexos, com rapidez e confiabilidade. O uso
da impressora permite a documentação dos resultados, com os pontos determinados,
características de elementos geométricos, parecer quanto a testes de tolerâncias, etc.
(figura 16.1).
c) MMC com Comando Numérico (CNC) e computador (figura 9.8). Com este
sistema dispõe-se da capacidade de programar a medição de uma peça, que desenrolar-
se automaticamente. O programa é armazenado no computador, que transfere os
comandos específicos ao CNC.
10

140. A figura 9.12 mostra o resultado apresentado na medição dos flancos dos dentes de
uma engrenagem, de modo totalmente automático. Como resultado obtém-se um gráfico
com a representação dos erros dos flancos em relação à geométrica ideal pré-definida.
O programa de medição de uma peça pode ser gerado por um computador de maior
porte, dotado de um software que elabora a estratégia de medição a partir da geometria
nominal da peça. Mais usual entretanto é a técnica de programação por aprendizado. A
medição da primeira peça
(ou padrão) é realizada semi-automaticamente por um operador especializado que define
os pontos de medição, estabelece a seqüência de medição, o percurso do apalpador e
informa os valores nominais da geometria e a respectiva tolerância. Nesta primeira fase,
o computador permanece no modo “aprendizado”, onde vai armazenando
seqüencialmente todas as informações de operação. Para as demais peças, o
computador é colocado no modo “medição”, repete todo o ciclo, efetuando o controle,
o processamento e a documentação
pré-estabelecidos;
Figura 9.12: Exemplo de relatório gráfico resultante da medição de coordenadas.
d) MMC integrada a sistemas de fabricação. Uma MMC (figura 9.13) ou um centro
de medição (figura 9.14), controlados por CNC, permite um controle geométrico de
peças com grande velocidade e flexibilidade na alteração de programas de medição.
dispõe-se de recursos como troca automática de sensores (figura 9.13) ou apalpadores
(figura 9.14), bem como alimentação por palets ou robôs (figura 9.18).
11

141. Figura 9.13: Máquina de medir por coordenadas com proteção contra o ambiente e troca
automática de sensores.
Figura 9.14: Centro de medição com dois cabeçotes de medição e troca automática de
sensores.
12

142. Figura 9.15: Máquina de medir por coordenadas (1).
13

143. Figura 9.16: Software de controle manual com capacidades 3D.
9.7 ASPECTOS ECONÔMICOS
O custo de uma MMC ainda é bastante alto. Nos países desenvolvidos, onde a
mão de obra tem um custo muito elevado, a medição de uma peça com certo grau de
complexidade já é significativamente mais econômica com uma MMC do que aplicando
a instrumentação clássica. Na avaliação comparativa dos custos, devem ser considerados
aspectos como: custo do investimento, depreciação, custo da área de trabalho, facilidade
para preparação da medição (programas), tempo de medição, tempo de processamento,
manutenção dos sistemas e assistência pós-venda, tamanho dos lotes, capacidade de
comunicação com outros sistemas computacionais (troca de dados), etc.
14

144. Não são computados no estudo econômico as vantagens para o sistema produtivo
advindos de um tempo de controle bastante reduzido, especialmente, quando se trata de
verificação de peças ponta de série, com a finalidade de checar a regulagem das
máquinas. Outro aspecto favorável, difícil de traduzir financeiramente, é a possibilidade
de solucionar problemas metrológicos de difícil solução com os recursos clássicos.
Figura 9.17: Máquina de medir por coordenadas (2).
Figura 9.18: Centro de medição com alimentação de peças por robô.
A implantação de um sistema de medição por coordenadas exige um estudo
técnico-econômico aprofundado e uma adaptação conveniente do sistema de controle de
qualidade (especificações em desenhos, por exemplo).
15

145. No intuito de racionalizar a produção e de garantir a qualidade dos produtos,
existe a necessidade de se identificar os erros geométricos das peças o mais cedo
possível, o que exige um alto grau de automatização e flexibilidade dos sistemas de
medição e controle. A atuação do computador será gradativamente mais ampla,
aumentando ainda mais a potencialidade da tecnologia de medição por coordenadas.
16

146. Capítulo 10
AUTOMAÇÃO DO CONTROLE DIMENSIONAL
10.1 INTRODUÇÃO
A utilização do computador na metrologia dimensional e/ou controle de qualidade
geométrica não é uma questão de racionalização de mão-de-obra e sim, em primeiro
plano, a própria viabilização econômica e/ou técnica da medição.
Através do computador, seja ele dedicado (embutido no sistema de medição) ou de uso
genérico (microcomputador) alcança-se:
- Redução dos erros de medição de forma a tornar o instrumento adequado (à tarefa de
controle geométrico;
- Rapidez, de forma que o processo tornar-se economicamente viável dentro do processo
produtivo;
- Solução de problemas complexos de aquisição e processamento dos dados,
viabilizando tecnicamente a medição;
- Viabilização de manipulação de grande volume e em curto intervalo de tempo, de
forma a produzir informações sobre o andamento (instantâneo) do processo produtivo;
- Simplificação da mecânica e da eletrônica tornando os sistemas de medição
relativamente mais baratos.
Figura 10.1: CQ-dimensional ; Medição diferencial.
1

147. A tendência que se observa no campo do controle de qualidade geométrico é
visualizada na figura 10.1. A informação sobre a situação geométrica do componente-
produto é buscada com o intuito de verificar se a peça está dentro ou fora das
tolerâncias, isto é, se é boa ou não. O controle dimensional do produto acabado, como
única operação de controle na processo produtivo, pode ser altamente prejudicial em
função de refugo de grandes lotes e de ser altamente sujeito a erros. Isto faz com que
estações de controle sejam levadas junto ao processo de usinagem com o intuito de
identificar, mais cedo, o aparecimento de peças fora de comportamento dos meios de
produção e, através de realimentação, corrigir o processo de forma que não se efetive o
aparecimento de dimensões fora de tolerâncias, isto é, produção com “refugo zero”.
Exemplos são os sistemas automatizados de controle estatístico junto ao processo de
fabricação.
Na seqüência, é feita uma abordagem acerca das estações computadorizadas de
medição e das técnicas de integração da medição nos processos de fabricação.
10.2 ESTAÇÕES AUTOMÁTICAS DE MEDIÇÃO
As estações independentes e automatizadas com o uso do computador buscam um ou
mais objetivos citados no item primeiro. Destacam-se as que operam:
a) Pelo método diferencial
Com a utilização de um ou múltiplos transdutores elétricos de deslocamento (figura
10.2) é possível realizar com grande rapidez o controle geométrico de diversos
parâmetros, emitindo-se de forma imediata um laudo sobre o componente ou sobre o
lote de peças controlado.
Figura 10.2: Medição de deslocamento usada no controle dimensional de peças.
b) Pela técnica de medição por coordenadas
A máquina de medir por coordenadas (figura 10.3) é o sistema de medição mais
universal existente. A sua viabilização prática deu-se em função do computador, que
assume os complexos e extensivos cálculos da geometria a partir das coordenadas de
pontos sobre a superfície a caracterizar. Nas configurações mais modernas, além de
2

148. assegurar pequena incerteza de medição em um grande volume de trabalho, o operador
“ensina” o sistema medindo um padrão e posteriormente a máquina realiza
automaticamente o completo controle dos demais componentes a controlar.
Figura 10.3: Máquina de medir coordenadas (tridimensional).
c) Aplicando recursos eletroópticos
Com o intuito de, entre outras razões evitar retroação sobre o objeto, de simplificar ou
eliminar dispositivos de medir durante uma operação de fabricação ou transporte,
desenvolvem-se intensos trabalhos de pesquisa em sistemas de medição eletroópticos,
utilizando laser, fotodetetores, câmaras de vídeo, etc.
Um exemplo de sistema de medição por varredura a laser é mostrado na figura 10.4.
Este sistema é capaz de medir a dimensão de uma peça cerca de 250 vezes por segundo
em uma faixa de operação de até 40 mm com incerteza de medição de ± 5 µm. Além de
atender situações estáticas, onde a peça a medir está parada, este sistema é também
adequado a medição em processos contínuos, como por exemplo a extrusão, onde o
elemento fabricado pode passar pelo sistema de medição com velocidades de até 120
km/h.
Este sistema possui recursos estatísticos para avaliar o valor médio, máximo, mínimo e
a dispersão do lote de peças medindo (ou do trecho amostrado no caso de processos
contínuos). Outra característica interessante é o fato deste sistema comparar o valor
medido com um valor de referência e enviar um sinal analógico proporcional a esta
diferença que é muitas vezes usado para realimentar a máquina e corrigir os desvios do
processo.
3

149. Figura 10.4: Micrômetro laser.
10.3 CONTROLE DIMENSIONAL NO PROCESSO
De acordo com a figura 10.5, pode-se classificar os modos de realização do controle
de qualidade dimensional das peças em função da localização e atuação de medição
relativamente à unidade de fabricação. O objetivo dos sistemas será assegurar a
qualidade dimensional e elevar o grau de utilização dos meios de produção (reduzir
custos), sendo o segundo, por vezes, o resultado mais significativo do método.
Figura 10.5: Controle de qualidade dimensional ; localização das estações de medição.
10.3.1 Controle próximo à Unidade de Fabricação
Especialmente quando se trata da usinagem de peças complexas, o início da produção
de um lote só é liberado após a aprovação da peça piloto. O controle dimensional
correspondente é realizado, em geral, na sala de metrologia do setor. Este procedimento,
4

150. bastante demorado pode ser otimizado com um sistema como configurado na figura
10.6. A máquina de medir por coordenadas seguir um programa de medição pré-
estabelecido, e os resultados são levados máquina-ferramenta correspondente através da
rede de comunicação. Esta etapa antecipa significativamente o início da fabricação, eleva
a segurança das informações e permite realimentar automaticamente o comando
numérico (CNC) com valores que otimizam a incerteza da fabricação. Esta técnica pode
ser estendida a outras amostras durante a produção do lote, sendo, neste caso, a
operação de medição efetuada em paralelo, mas com realimentação de informações
para o processo.
Como pode ser facilmente concluído, uma máquina de medir pode atender diversas
unidades de fabricação.
Figura 10.6: Máquina de medir por coordenadas ; conexão ao sistema de controle do
processo.
10.3.2 Controle junto à Unidade de Fabricação
A medição junto à máquina-ferramenta, com auxílio de instrumentos convencionais, é
prática comum nos processos de fabricação não automatizados. Estes mesmos
procedimentos podem ser integrados a um controle do processo, quando se passa a
utilizar instrumentos modernos, isto é, com informação elétrica, que pode ser processada
automaticamente e realimentar o processo (figura 10.7).
5

151. Figura 10.7: Instrumentos e dispositivos de medição ligados ao sistema de controle do
processo.
Seja por um dispositivo de medição múltipla ou por instrumentos digitalizados que
atendam uma, duas ou mais unidades de fabricação próximas, o controle dimensional de
todas as peças produzidas, ou de amostras, permite manter o processo de fabricação em
faixas de tolerâncias bastante estreitas. Auxilia também na monitoração da unidade de
fabricação quanto à troca de ferramentas, identificação do estado de regime estabilizado,
etc.
Pelo fato do controle ser pós-processo de usinagem, é importante que o sistema de
análise identifique a tendência em cada dimensão e proceda correções preventivas na
unidade de fabricação, para que as dimensões das peças subsequentes sejam
devidamente posicionadas no campo de tolerância.
A operação de medição pode ser feita por operador ou por robô industrial,
especialmente quando este equipamento já está presente para realizar a alimentação da
unidade de fabricação.
Para peças mais complexas, produzidas dentro de uma “linha transfer” ou célula flexível
de fabricação, pode-se colocar junto à unidade de fabricação, máquinas de medição por
coordenadas, como mostrado na figura 10.8. Um processador especial faz a
interpretação das informações e comanda a realimentação do processo de usinagem.
10.3.3 Controle dentro da Unidade da Fabricação
Compreende as medições que são realizadas enquanto a peça permanece acoplada à
unidade de fabricação para a usinagem. Estas medições podem ocorrer de forma
intermitente ou simultaneamente à operação de usinagem.
6

152. Figura 10.8: Medição por coordenadas ; integração a uma linha transfer.
a) Medição Intermitente à Usinagem
É realizada antes do início, durante pausas ou após concluída a operação de usinagem
da peça, em determinada máquina. A medição de um ou mais parâmetros geométricos
pode ser realizada através de:
- Dispositivos de medição que são posicionados e acionados pela própria máquina,
pelo operador ou por robô (figura 10.9). Neste caso a incerteza de medição é bastante
independente do manipulador e o dispositivo é bastante específico para a grandeza/peça
a medir;
- Recursos da própria máquina-ferramenta. Destacam-se aqui os sistemas de medição
por coordenadas no processo (SMCP).
Neste segundo caso aproveita-se os recursos de movimentação programada das
máquinas com comando numérico. No momento da medição acopla-se um apalpador
eletrônico no lugar de uma ferramenta de corte, como mostrado na figura 10.10.
Obedecendo a comandos específicos de posicionamento e medição, pode-se
determinar as coordenadas espaciais de pontos sobre a peça, que processadas
devidamente permitem determinar os parâmetros geométricos reais da peça em
fabricação. As diferenças para os valores desejados dão subsídios para geração de
comandos de correção, que são levados ao comando numérico.
b) Medição Simultânea à Usinagem
Enquadram-se aqui os sistemas de realimentação direta, do tipo freqüentemente
empregados na retificação de peças cilíndricas (figura 10.11). Apesar de ser o método
mais próximo do ideal, pelo fato de efetuar o controle contínuo da grandeza e de forma
7

153. simultânea ao processo de usinagem (sem tempos secundários), a sua realização prática
tem-se mantido muito restrita em função de falta de sensores adequados, que possam
operar sem interferência das rudes condições de usinagem.
Figura 10.9: Dispositivos de medição ; manual – máquina - robô.
Figura 10.10: Sistema de medição por coordenadas no processo.
8

154. Figura 10.11: Medição simultânea ao processo de fabricação.
10.4 INTEGRAÇÃO DA INFORMAÇÃO
Os objetivos do controle da qualidade dimensional no processo só poderão ser
alcançados quando as informações geradas pela medição puderem ser interpretadas
com rapidez e, de imediato, os resultados ou as eventuais ações saneadoras possam ser
levadas aos meios de produção. Fica evidente a necessidade da comunicação de
sistemas de medição computadorizados, bem como a necessidade de comunicação
destes com as unidades de fabricação.
Efetivamente este desenvolvimento vem sendo observado de modo crescente, mas em
geral, com soluções particularizadas.
A necessidade de uma padronização na comunicação entre estações inteligentes
instaladas no meio industrial tem estimulado no transcorrer dos últimos anos vários
trabalhos de desenvolvimento e normalização.
Uma vez viabilizada esta comunicação entre estações de medição e unidades de
fabricação, bem como, com estações centrais de programação, monitoração e
documentação, o fluxo de informações passa a se estender a todos os outros problemas
da produção, não se restringindo aos dados sobre o controle de qualidade.
Na figura 10.12 exemplifica-se a interligação de diversas estações de medição,
mostrando-se inclusive aspectos relativos à automatização do controle estatístico no
processo, cujas informações, além de garantirem e documentarem a qualidade dos
produtos em fabricação, reúnem informações relevantes sobre a capacitação do sistema
produtivo.
9

155. Figura 10.12: Rede de comunicação local, interligando estações de medição (EM), com
possibilidade de controle estatístico do processo via estação e documentação.
10

156. Capítulo 11
MEDIÇÃO DE ROSCAS
11.1 GEOMETRIA DE ROSCAS
São 5 ( cinco ) os elementos principais que definem uma rosca cilíndrica ( veja a
figura 11.1, letras minúsculas para o parafuso, maiúsculas para a porca ), ou seja:
- diâmetro externo d, D;
- diâmetro do núcleo d1, D1;
- diâmetro de flancos d2, D2;
- passo h;
- ângulo de flancos α, sendo os semi-ângulos de flancos α1 e α2.
Na figura 11.1a, encontram-se estes elementos desenhados num corte axial que
passa pelo eixo da rosca. Apenas neste plano aparecem os flancos da rosca como retas,
sem distorção.
Para roscas cônicas, outro parâmetro importante é a conicidade da rosca. Os
elementos de uma rosca métrica cônica podem ser identificados na figura 11.2.
Para a medição de roscas o diâmetro de flancos é de máxima importância. É
definido como a distância ( medida perpendicularmente ao eixo da rosca ) dos dois
flancos opostos, medida nos pontos A ( figura 11.1a ) que se encontram na linha central
( na metade ) dos flancos de um perfil teórico completo ( pontiagudo, com profundidade
t na figura 11.1.a).
Na figura 11.1a ficam esclarecidos também outros elementos adicionais da rosca:
- a profundidade t do perfil teórico ( definindo as grandezas t/2 em relação à linha
central dos flancos );
- a profundidade t1 da rosca ( tanto para o parafuso como para a porca );
- a profundidade t2 do assento, ou seja, da sobreposição dos flancos do parafuso e
porca;
- os arrendondamentos do perfil.
Além dos elementos de rosca mencionados, usam-se ainda, as seguintes grandezas
calculadas:
- as folgas, sendo:
a folga nas pontas do diâmetro externo a = (1/2) . (D - d)
a folga nas pontas do diâmetro do núcleo b = (1/2) . (D1 - d1)
a folga nos flancos s = (1/2) . (D2 - d2)
1

157. - o ângulo de avanço ∅, sendo tg ∅ = h/(d2)
ou, para os ângulos pequenos, quando a tangente fica substituída por ângulos em
radianos.
∅ (graus) = 18,25 (h/d2)
Em construção de máquinas usam-se roscas de vários perfis: roscas métricas,
roscas Whitworth, Edison, Laewenhertz, entre outras.
Figura 11.1: Elementos principais de uma rosca.
Figura 11.2: Rosca métrica externa cônica.
Atualmente a rosca mais usada é a métrica, M, escalonada de acordo com o
diâmetro externo d, D, chamado nesse contexto, diâmetro nominal da rosca e
caracterizada por este diâmetro junto com o valor do passo, qualidade de fabricação e
posição da tolerância, conforme mostra a figura 11.3.
2

158. Para a rosca métrica o valor do ângulo de flanco é 60° ( sendo os semi-
ângulos α1 = α2 = 30° ). Além disso a norma ABNT NB97, entre outras, prescreve
quais diâmetros nominais devem ser usados preferencialmente, quais diâmetros são
complementares, de forma que a combinação do diâmetro nominal com certo valor
numérico do passo deve ser considerado como normal, e quais combinações podem ser
usadas opcionalmente: as normas prescrevem também os valores numéricos de t, t1, t2,
arredondamentos, etc.
Outros tipos de roscas têm as suas dimensões e outros elementos definidos
também pelas respectivas normas. Para calibradores de rosca métrica, a norma NBR-
8225 especifica os valores nominais, tolerâncias de fabricação e tolerância de desgaste.
Figura 11.3: Designação de roscas métricas.
11.2 MÉTODOS DE MEDIÇÃO DE ROSCAS
A medição de roscas é abordada tradicionalmente em medição de roscas externas
( isto é, roscas tipo parafuso ), e medição de roscas internas ( tipo porca ).
Apesar de terem os métodos alguns procedimentos em comum, há bastante
diferenças entre eles. Além disso, a medição de roscas internas é mais complexa e o
número de métodos aplicáveis bastante reduzido.
11.2.1 Comparação dos Métodos Ópticos e Mecânicos
Na medição de roscas externas, dispõe-se, basicamente, de dois grupos distintos
de métodos: há métodos mecânicos de medição ( mais antigos ) e, recentemente,
3

159. métodos ópticos de medição de roscas, caracterizados pelo uso de um microscópio (
com vários acessórios ).
Métodos Mecânicos de Medição de roscas estão sujeitos a certas limitações. Por
exemplo a medição por meios mecânicos do ângulo do perfil não é aplicável, a não ser
para grandes valores de passo e com uso de máquinas de medir especiais. Já a
medição do diâmetro do núcleo exigiria o uso de apalpadores de medição especiais e o
resultado ficaria fortemente influenciado pelo tipo de contato destes apalpadores no
fundo do perfil e pela força de medição utilizada, de modo que a confiabilidade do
resultado ficaria comprometida.
Deste modo, os métodos mecânicos de medição limitam-se à verificação do
diâmetro externo, do passo e, com grande importância, à verificação do diâmetro de
flancos. Estas três medições serão abordadas mais adiante.
Métodos ópticos são caracterizados pelo uso de um microscópio. Todos os
parâmetros de uma rosca externa, inclusive o ângulo do perfil e diâmetro do núcleo, são
mensuráveis sem problemas, já que o procedimento é direto: mede-se cada um dos
parâmetros independentemente dos outros, evitando-se a influência mútua com o
subsequente mascaramento dos resultados. Nas roscas internas é possível medir-se
apenas os semi-ângulos de flanco, através da confecção de uma " amostra " do perfil
real do ângulo da rosca, feita de material com características de deformação
volumétrica muito pequena.
Todos os parâmetros da rosca externa são medidas na mesma máquina de medir
( microscópio de medição ) durante uma única montagem. Os valores numéricos são
obtidos sem cálculos intermediários complexos.
Comparando os métodos mecânicos e ópticos, pode-se tecer as seguintes
observações:
- a incerteza de medição ( erro máximo ) dos resultados obtidos com métodos
mecânicos na maioria dos casos é menor do que aqueles obtidos com métodos
ópticos;
- os métodos ópticos são mais universais permitindo a medição de todos os
elementos da rosca, sem exceção;
- genericamente, os métodos mecânicos apresentam certas vantagens na verificação
da produção em série. Nesta situação, são mais rápidos e os instrumentos
convencionais necessários mais baratos;
- com o surgimento das máquinas de medir por coordenadas, os métodos
mecânicos passaram a ser mais utilizados para a medição de parâmetros como
diâmetro de flancos, passo e conicidade; o ângulo de flancos é um parâmetro que
ainda se obtém melhores resultados com os modernos microscópios de medição.
4

160. 11.2.2 Métodos Mecânicos de Medição de Roscas
a) Medição do diâmetro externo
A medição do diâmetro externo de roscas por meios mecânicos não difere das
medições externas de cilindros lisos.
Devem ser levadas em consideração em cada lado da rosca pelo menos duas
cristas dos filetes. No caso de passos grandes pode-se lançar mão de corpos auxiliares
como por exemplo, dois blocos padrão a cada lado da rosca.
b) Medição do passo
Na medição do passo de roscas é possível usar dois procedimentos diferentes:
- medição sobre um flanco;
- medição sobre dois flancos vizinhos, ou seja, medição entre " cristas da rosca ".
Na figura 11.4.a, tem-se o perfil de rosca com a marcação nítida do flanco
esquerdo do perfil e do flanco direito.
Segundo a definição, o passo ( n na figura 11.4.a) é a distância entre dois flancos
consecutivos ( esquerdos ou direitos ).
Se o perfil for ideal, com o passo perfeitamente constante ao longo da rosca, o
passo aparece também entre quaisquer pontos do perfil, como por exemplo, entre "
cristas da rosca " (n* na figura 11.4a). Se por outro lado, houver erros locais de passo,
os dois procedimentos lembrados oferecem resultados um tanto diferentes. Neste caso,
como resultado mais correto, deve ser considerado aquele obtido de acordo com a
definição do passo, ou seja, obtido pela medição sobre um flanco só.
Figura 11.4: Medição do passo.
5

161. Nos dois métodos apalpa-se o flanco ( ou os flancos ) com algum apalpador de
medição conveniente. O mais frequente nos métodos mecânicos é o apalpador com
ponta esférica. No primeiro método encosta-se o apalpador sempre sobre o mesmo tipo
de flanco ( por exemplo, sempre o esquerdo ) e mede-se o referido deslocamento do
apalpador. Este método é menos seguro, visto que o posicionamento pode não ocorrer
sempre na mesma altura dos flancos consecutivos.
No segundo método, o apalpador é introduzido entre os filetes da rosca até
encostar nos dois flancos vizinhos, figura 11.4b. Nesta posição o centro do apalpador
coincide com a linha de simetria do filete da rosca (α1 = α2 = α/2, na figura 11.1a).
Medindo-se em seguida o deslocamento do apalpador para o filete seguinte ( medida h
na figura 11.4b ), tem-se o valor de um passo. Neste método, porém, é bastante
comum deslocar o apalpador em mais do que um filete, como por exemplo, em 5
filetes, obtendo-se depois o passo médio da rosca ( figura 11.4b ).
Algumas máquinas de medir mecânicas, destinadas a realizar a verificação do
passo médio usando o segundo método acima descrito, dispõem de apalpadores
cônicos que são ajustados para a medida correta por intermédio de calços-padrão que
fazem parte dos acessórios das máquinas de medir.
c) Medição do diâmetro de flancos por meio mecânico
A medição do diâmetro de flancos é uma das mais importantes, pois caracteriza a
rosca em projetos de dimensionamento.
Dificuldades surgem porque o diâmetro de flancos não é diretamente disponível
para a medição. De acordo com a definição, o diâmetro em questão é a distância
medida perpendicularmente ao eixo da rosca na metade da altura do filete. Entretanto,
os flancos da rosca encontram-se na realidade deslocados axialmente em valor da
metade do passo. Além disso, a ponta central do flanco (onde dever-se-ia medir de
acordo com a definição) também não é direta e nitidamente marcada. Logo, não é
possível medir o diâmetro de flancos diretamente de acordo com a definição do mesmo.
Servir-se dos diâmetros externos e do núcleo como meios auxiliares para a
medição do diâmetro de flancos não é viável nem recomendável, já que estes dois
diâmetros são apenas parâmetros secundários para a definição e funcionamento da
rosca. Na fabricação dos mesmos não se cuida, por motivos econômicos, de suas
dimensões suficientemente para poder aproveitá-los como base de medição.
A solução encontrada e geralmente adotada é servir-se de elementos geométricos
auxiliares, como arames calibrados, cones, prismas, esferas, entre os filetes da rosca,
permitindo a medição do diâmetro de flancos.
Dois métodos comumente usados serão abordados a seguir.
6

162. c.1) O método dos três arames
O princípio deste método está esquematizado na figura 11.5. Num lado da rosca
coloca-se, entre dois filetes, um arame e no lado oposto da rosca, dois arames
semelhantes.
Os "arames" usados tem a forma de cilindros curtos com geometria de alta
qualidade e com diâmetros iguais e conhecidos.
Os três arames acomodam-se nos respectivos filetes tocando os flancos. O
diâmetro dos arames deve ser escolhido em função dos parâmetros da rosca a fim de
que toquem os flancos perto da linha média do flanco, e ao mesmo tempo, sobressaiam
aos filetes.
A medida Mo na figura 11.5a é tomada com algum instrumento de medição com
apalpadores planos, por exemplo, com uma Máquina de Medir, e a partir da mesma é
possível calcular o diâmetro de flancos. A medição em si é rápida e não exige máquinas
complexas, mas os cálculos necessários são incômodos. Para facilitá-los usa-se tabelas,
gráficos e/ou softwares específicos para esta finalidade. Tomando-se os cuidados
necessários e aplicando-se as correções devidas, os resultados obtidos são muito bons.
Fundamental é a incerteza de medição do instrumento/máquina de medir que é
utilizada para medir o valor de Mo.
Para se conseguir os melhores resultados, o diâmetro teórico dos arames a serem
utilizados deve ser calculado a partir da fórmula seguinte:
d = p , onde p é o passo da rosca . (11.1)
D 2.cos(α/ 2)
Arames com este diâmetro tocam o flanco exatamente na sua linha média, onde
teoricamente deveria ser medido o diâmetro. Na prática, porém, isto implicará em
grande quantidade de diâmetros dos arames ( para vários e vários h ). Por motivos
econômicos, são usados jogos de arames com diâmetros normalizados, sendo que
então faz-se necessária a devida correção matemática. Os diâmetros dos arames
normalizados são citados a seguir ( em mm ):
0,17 0,455 1,65
0,195 0,53 2,05
0,22 0,62 2,55
0,25 0,725 3,20
0,29 0,895 4,00
0,335 1,10 5,05
0,39 1,35 6,35
O procedimento de seleção do arame é realizado pelo uso da equação 11.1,
escolhendo-se o arame de diâmetro normalizado mais próximo do valor calculado.
Muito importante, para redução de erros sistemáticos durante o processo de
medição, é utilizar os diâmetros efetivos de cada arame de medição, obtidos pela
7

163. calibração dos mesmos, na equação de determinação do diâmetro de flancos. Por
exemplo, um erro no diâmetro dos arames igual a 1 µm, gera no diâmetro de flanco de
uma rosca métrica ( ângulo de flanco igual a 60 ° ) um erro sistemático de 3 µm.
O valor da leitura sobre arames pode ser deduzido se for estabelecida a premissa
de que no corte axial da rosca forem alojados não arames, mas sim, discos de
espessura infinitamente fina, com o diâmetro dD de arames. Neste caso a partir da
figura 11.5b, podem ser deduzidas as relações trigonométricas A,B, anotadas nesta
figura.
Este resultado tem valor apenas teórico, já que na realidade, a medição não é
feita por intermédio de discos finos ( como acima pressuposto ), mas sim com arames de
certo comprimento, que tocam os flancos em planos perpendiculares à hélice da rosca e
não no plano de corte axial. Portanto, o ângulo de flanco teórico que se estabelece com
o contato do disco fino não é o mesmo ângulo no qual ocorre o contato efetivo do
arame.
Figura 11.5: O método dos 3 arames.
Estas condições especiais de contato entre arames e flancos deve ser levada em
consideração pela correção δ 1 a ser substraída do resultado acima deduzido porque o
arame fica para fora da posição ideal, o que faz com que o valor de Mo seja maior do
que o correto.
O valor desta correção é:
d
δ = D . p . cos(α/ 2).cot g (α/ 2)
2 (11.2)
1 2 π2 d2
2
sendo apresentado, aqui sem dedução. Este valor pode ser encontrado também a partir
de tabelas especiais.
8

164. Como exemplo, tem-se, na figura 11.6a, uma tabela referente as roscas métricas
ISO normais. O valor M lido na 5a. coluna desta tabela vale para a força de medição
zero.
Figura 11.6: Método dos 3 arames ; correções devido à força de
medição.
Na realidade não se mede neste método com a força nula, de modo que ocorre o
" erro por achatamento " , ou seja, os arames se deformam sob a força de medição
verdadeiramente usada na medição, e o resultado obtido é menor do que sem
achatamento. O erro pode ser eliminado pela introdução de uma correção cujo valor
para α = 60º, é:
K2
C δ K = 0 , 86 . 3 (11.3)
dD
e que deve ser somada ao resultado anteriormente obtido.
Este valor pode ser obtido a partir do gráfico na figura 11.6b ou calculado como
produto entre o valor de δ K, retirado da penúltima coluna da tabela na figura 11.6a, e
o coeficiente C = 3 K 2 onde K é a força de medição em N.
Na figura 11.6b tem-se no eixo das ordenadas os diâmetros de arames dD em
mm e no eixo das abcissas lê-se o valor da correção CδK, em função das curvas para
9

165. diferentes forças de medição ( de baixo para cima, à direita, força K = 1 N; 1,5 N; 2,0
N; 2,5 N; 3,0 N e 10 N ).
Os valores de M dados nas tabelas são calculados para os valores dD dos arames
que constam do jogo normalizado e para os valores teóricos de α/2 = 30º (perfil
métrico perfeitamente simétrico) e do passo p também teoricamente correto. Se qualquer
destas grandezas sofrer alterações, torna-se imperativo, para se obter confiabilidade dos
resultados, introduzir correções adicionais. Apesar de que alguns elementos para o
cálculo das correções constarem na última coluna da tabela na figura 11.6a, não serão
os mesmos abordados neste curso. Portanto, a fórmula final para cálculo do diâmetro
de flanco fica sendo:
 dD  P
d2 = M 0 −
 sen(α / 2)  + 2 . cot g (α / 2) − d D − δ1 + CδK
 (11.4)
 
c.2) O método com cones e prismas
Os métodos está esquematizado na figura 11.7a. Os respectivos apalpadores
podem ser adaptados nas pontas de vários instrumentos de medição, sendo um dos
mais usados o micrômetro ( figura 11.7b e c ).
Figura 11.7: Medição de roscas ; método do prisma-cone.
O prisma deve ser inserido na ponta sem folga, porém, facilmente girável, já que
no momento da medição deve se acomodar sobre o flanco de acordo com o passo da
rosca.
O método é bastante comum em oficinas, já que oferece rapidamente os
resultados, sem cálculos adicionais e de fácil aprendizagem .
10

166. Porém, este método não deve ser empregado para um controle rigoroso do
diâmetro de flancos de calibradores de rosca, já que a incerteza de medição de
processo é elevada, isto é, não adequada para calibração destes padrões.
O maior problema reside na necessidade de se ter a coincidência perfeita entre os
perfis da rosca com o cone e o prisma. Qualquer erro angular em qualquer das peças
envolvidas, provocará erros de medição, como mostra nitidamente, em forma
exagerada, a figura 11.7d.
c.3) O método das duas esferas
A medição do diâmetro de flanco de roscas internas pode servir-se do princípio de
medições diferenciais segundo o método das duas esferas ( figura 11.8c). Como padrão
de referência para esta medição utiliza-se blocos padrão de comprimento em conjunto
com padrões especiais ( blocos de transferência ) que possuem, segundo o ângulo de
flanco da rosca a medir, chanfros de 55º ou 60º ( figura 11.8b ). A distância (a + b)
( figura 11.8b ) destes blocos especiais é conhecida, determinada por calibração.
Para a montagem do padrão de referência, existem basicamente dois
procedimentos. O primeiro utiliza um bloco padrão comum, montado entre os blocos de
transferência ( figura 11.8b ), de modo que o valor final do comprimento entre os
vértices dos flancos ( X na figura 11.8a ) seja um valor aproximado ao do diâmetro
de flanco da rosca a medir ( figura 11.8a ).
O valor " X " é calculado segundo a fórmula:
p2
(11.5)
X = d + p .cot g (α ) + 8
2 2 2 d
d + p .cot g (α ) − K
2 2 2 sen(α )
2
onde: d2 - diâmetro de flanco em mm
p - passo em mm
α - ângulo de flanco em graus
dK - diâmetro das esferas em mm.
O segundo procedimento, além de utilizar o bloco entre os padrões de
transferência, utiliza outro bloco sob um destes a fim de que haja uma defassagem entre
os flancos, correspondente ao valor do passo da rosca a medir ( figura 11.8d ).
Estudos experimentais constataram não haver diferença significativa entre os
resultados apresentados por um ou outro método.
11

167. Figura 11.8: Medição de roscas internas.
Assim como os arames de medição, as esferas também apresentam diâmetros
normalizados. Estes são 0,7; 0,8; 0,9; 1,35; 1,7; 1,8; 2,3; 3,1 e 3,3 mm .
O processo de medição do diâmetro de flancos de roscas internas é mais
complexo do que o método dos três arames, exigindo muita atenção no seu
equacionamento e durante as medições.
A medição é realizada com auxílio de uma máquina de medir que apresenta
dispositivos e acessórios especiais.
O método do cone-prisma é utilizado com frequência para medição de roscas
internas ( figura 11.7c). Porém, a incerteza de medição deste método, a exemplo das
roscas externas, não é adequada para realizar a calibração de calibradores.
A calibração de calibradores de rosca exige máquinas de medir de alta qualidade,
como por exemplo as que se utilizam do princípio de ABBÉ.
11.2.3 Método Óptico de Medição de Roscas Externas
Como já lembrado, os métodos ópticos são caracterizados pelo uso de um
microscópio.
O microscópio para medição de roscas é projetado para esta finalidade, com a
vantagem de disporem de oculares especiais chamadas pelo fabricante de " oculares-
revólver ". Cada ocular é constituída de uma placa giratória de vidro, com vários
desenhos de roscas e traços perfeitamente delineados, obtidos por gravação a ácido. As
12

168. figuras gravadas aparecem no campo visual do microscópio junto com a imagem da
rosca a ser medida.
Basicamente, dois são os métodos utilizados para medição óptica do diâmetro de
flanco. Embora os métodos sejam diferentes, não são necessários cálculos complexos na
obtenção dos valores efetivos.
a) Processo de intersecção dos eixos:
A medição por este processo é feita tangenciando os gumes das facas de medição
nos flancos da rosca, num plano horizontal, coincidente com o eixo axial do calibrador.
Estas facas tem, paralelamente ao gume, um traço fino que é utilizado como linha
auxiliar nas medições. Esta linha auxiliar é coincidente com o espaçamento entre os
reticulados na ocular goniométrica para determinadas aplicações pré-definidas.
Neste processo, o cabeçote do microscópio deve permanecer na posição vertical
( inclinação zero).
Utiliza-se também, ao mesmo tempo, iluminação diascópica ( de baixo para cima
) para visualização do flanco, e episcópica ( de cima para baixo ) para observação do
traço na faca de medição.
A medição consiste em tangenciar o retículado à linha de medição da faca em um
lado da rosca e a seguir, dando um deslocamento do calibrador apenas na direção
perpendicular à axial, tangenciar o retículado no lado oposto da rosca.
A diferença entre as leituras realizadas é o valor do diâmetro de flanco da rosca.
b) Processo de Duplicação do Perfil
Uma ocular de duplicação, através de um prisma, duplica e inverte o perfil da
rosca, permitindo uma simulação de acoplamento ( encaixe ) da imagem duplicada com
o perfil real da rosca. As leituras obtidas através da simulação deste acoplamento dos
dois lados da rosca determinam o valor do diâmetro de flanco efetivo.
A medição do diâmetro externo, diâmetro de núcleo, passo e ângulos de flanco
são feitas diretamente nos oculares comuns.
Na figura 11.9a, tem-se o exemplo do campo visual de um microscópio munido
com ocular/revólver para as roscas métricas.
O contorno do perfil da rosca a ser medido é desenhado na figura com traço
grosso. Os perfis que constam da placa giratória da ocular-revólver aparecem em linha
tracejada com números indicando o passo de cada um dos perfis.
No campo visual aparece uma escala em graus ( a margem esquerda do campo
visual na figura 11.9a ) para o posicionamento correto de perfis da placa giratória.
Deve-se lembrar ainda que no campo visual aparece, de uma vez, só parte dos
13

169. desenhos gravados; o resto é visível ao girar a placa por intermédio do parafuso
apropriado.
Para se ter uma idéia de todos os desenhos que constam em uma das placas, na
figura 11.9b, tem-se o caso bastante típico da placa giratória para a medição de roscas
métricas ISO.
Constam na placa:
- no segmento A, os perfis métricos corretos para os passos de 0,075 até 6 mm;
- R - duas figuras perpendiculares, com traços duplos, usadas como miras para o
começo e o fim de um caminho de medição, na direção dos eixos X e Y,
respectivamente;
- C - uma escala para a medição rápida de 0,01 até 0,1 mm;
- D - duas escalas horizontais e uma vertical com divisões correspondentes a 0,02
mm, sendo a extensão total de cada escala de 4 mm. Estas escalas servem para a
medição rápida de profundidades de roscas, acabamentos de pontas de roscas,
etc.;
- E - linhas tracejadas oblíquas, com ângulo de 60º (intercalados com escalas D),
usadas para a medição do ângulo de flancos;
- F - uma cruz de fios, tracejada, para a medição de ângulos pequenos ( até ± 7º )
junto com a escala na ocular ( compare na figura 11.9a a escala na extrema
esquerda ), para medição com apalpador adicional e outras medições;
- G - uma figura de traços duplos, com 60º para a medição de passos de roscas.
Figura 11.9: Método óptico de medição de roscas.
14