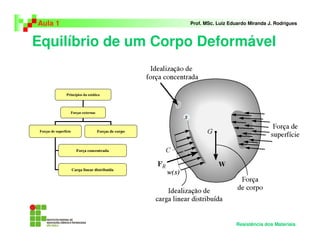
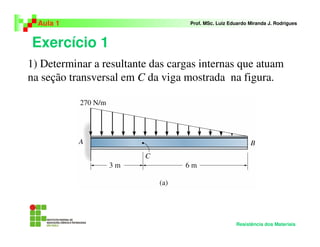
Este documento apresenta a primeira aula de um curso de Resistência dos Materiais. A aula introduz conceitos básicos como definição de Resistência dos Materiais, equações de equilíbrio da estática e carga interna resultante. Exemplos e exercícios são fornecidos para demonstrar o cálculo da carga interna em diferentes situações de carregamento.