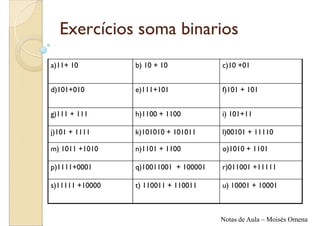
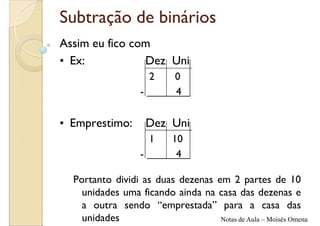
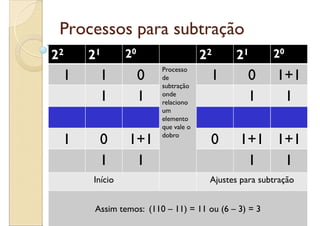
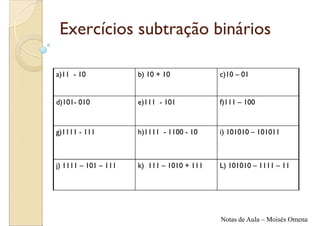
O documento apresenta informações sobre montagem e manutenção de computadores. São apresentados exercícios de soma e subtração binária, com as respectivas respostas. São explicados os processos de subtração binária, como emprestar valores das casas à esquerda.

1. Montagem e
Manutenção de
computadores
Notas de Aula – Moisés Omena

2. Montagem e
Manutenção de
computadores
Instituto federal de Ensino
Superior - IFES
Prof. Moisés Omena
Notas de Aula – Moisés Omena

3. Exercícios soma binarios
a)11+ 10 b) 10 + 10 c)10 +01
d)101+010 e)111+101 f)101 + 101
g)111 + 111 h)1100 + 1100 i) 101+11
j)101 + 1111 k)101010 + 101011 l)00101 + 11110
m) 1011 +1010 n)1101 + 1100 o)1010 + 1101
p)1111+0001 q)10011001 + 100001 r)011001 +11111
s)11111 +10000 t) 110011 + 110011 u) 10001 + 10001
Notas de Aula – Moisés Omena

4. Respostas Exercícios de Soma
a)11+ 10 = 101 b) 10 + 10 =100 c)10 +01 = 11
d)101+010 = 111 e)111+101=1100 f)101 + 101 = 1010
g)111 + 111 = 1110 h)1100 + 1100 =11000 i) 101+11 = 1000
j)101 + 1111 = 10100 k)101010 + 101011 = l)00101 + 11110 =
1010101 100011
m) 1011 +1010= 10101 n)1101 + 1100 = 11001 o)1010 + 1101 =10111
p)1111+0001 = 10000 q)10011001 + 100001 r)011001 +11111 =
10111010 111000
s)11111 t) 110011 + 110011 = u) 10001 + 10001
+10000=101111 1100110 =100010
Notas de Aula – Moisés Omena

5. Subtração de binários
• Quando um valor é menor que o total que deve ser
reduzido do mesmo, pedimos “emprestado” para a
casa imediatamente a esquerda desse número.
• Ex: 20 – 4
20
-4
16
Aqui, existem duas dezenas e quatro unidades, a casa da
dezena deve emprestar para a casa das unidades visto que
não posso retira 4 de zero. Assim empresto 10 unidades
para a casa das unidades (ou seja, uma dezena) e subtraio
estas dez unidades da casa das dezenas.
Notas de Aula – Moisés Omena

6. Subtração de binários
Assim eu fico com
• Ex: Dez Uni
2 0
- 4 .
• Emprestimo: Dez Uni
1 10
- 4 .
Portanto dividi as duas dezenas em 2 partes de 10
unidades uma ficando ainda na casa das dezenas e
a outra sendo “emprestada” para a casa das
unidades Notas de Aula – Moisés Omena

7. Processos para subtração
Dezenas Unidades Dezenas Unidades
Processo de
2 0 subtração onde 1 10
relaciono uma
dezena com 10
unidades, para
0 4 extrair as
unidades
0 4
necessárias ao
cáulculo
Início Ajustes para subtração
Assim temos: (10 – 4) + ( 10 ) = 16
Notas de Aula – Moisés Omena

8. Subtração de binários
• Quando um valor é menor que o total que deve ser
reduzido do mesmo, pedimos “emprestado” para a
casa imediatamente a esquerda desse número.
• Ex: 110 – 11
110
- 11
Aqui, funciona da mesma forma, (pediremos emprestado)
mas ao inves de uma dezena, o valor imediatamente a
esquerda vale o dobro do valor da casa onde esta sendo
feita a operação, portanto, quando pego um emprestado
da coluna a esquerda , na verdade estou pegando (1 x 2)
ou seja I + I .
Notas de Aula – Moisés Omena

9. Subtração de binários
Assim eu fico com
• Ex: 22 21 2º
1 1 0
- 1 1 .
• Ex: 22 21 2º
1 0 1+1
- 1 1 .
Portanto empresto para cada casa a direita o dobro do valor que ela
possui, e reduzindo-se 2 de 1 tenho 1 como resultado. Prosegue-se
com o mesmo procedimento para as outras casas a esquerda.
Lembrando que: 22 = 21 + 21 e 21 = 20 + 20 (dobro do número a direita)
Notas de Aula – Moisés Omena

10. Processos para subtração
22 21 20 22 21 20
Processo
1 1 0 de 1 0 1+1
subtração
1 1 onde
relaciono
1 1
um
elemento
que vale o
dobro
1 0 1+1 0 1+1 1+1
1 1 1 1
Início Ajustes para subtração
Assim temos: (110 – 11) = 11 ou (6 – 3) = 3
Notas de Aula – Moisés Omena

11. Subtração de binários
• efetuar 111012 - 10012
11101 (29)
- 1001 (9)
10100 (20)
• efetuar 1012 - 1112 - 102
101
- 111
- 10
000
Este cálculo esta correto???
Notas de Aula – Moisés Omena

12. Subtração de binários
• efetuar 1012 - 1112 – 102 (De modo correto)
• A primeira coisa a fazer é somar os elementos comuns
conforme o sinal portanto
11
- 111
- 10
1001
Portanto agora temos os elementos de mesmo sinal
agrupados e podemos realizar a operação (lembrando
que subtraimos referenciando o maior valor, que é o que
determinará o sinal do resultado.
- 1001 - 0201
+ 101 + 101
00 - 0100
Notas de Aula – Moisés Omena

13. Exercícios subtração binários
a)11 - 10 b) 10 + 10 c)10 – 01
d)101- 010 e)111 - 101 f)111 – 100
g)1111 - 111 h)1111 - 1100 - 10 i) 101010 – 101011
j) 1111 – 101 – 111 k) 111 – 1010 + 111 L) 101010 – 1111 – 11
Notas de Aula – Moisés Omena

14. Respostas Exercícios de
subtração
a)11 - 10 = 01 b) 10 + 10 = 00 c)10 - 01 = 01
d)101- 010 = 011 e)111 - 101=010 f)111 - 100 = 011
g)1111 - 111 = 1000 h)1111 - 1100 - 10 i) 101010 - 101011 =
=0001 - 000001
j) 1111 – 101 – 111 = k) 111 – 1010 + 111 = L) 101010 – 1111 – 11 =
11 100 11000
Notas de Aula – Moisés Omena