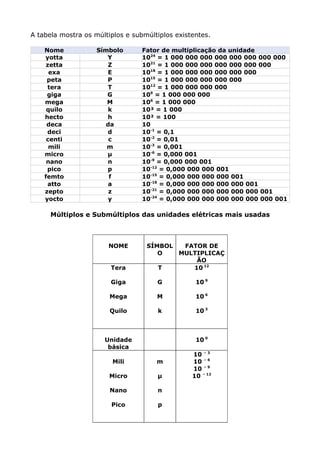
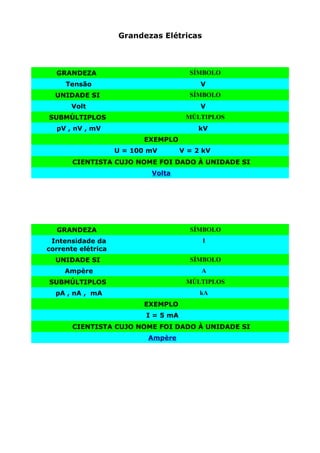
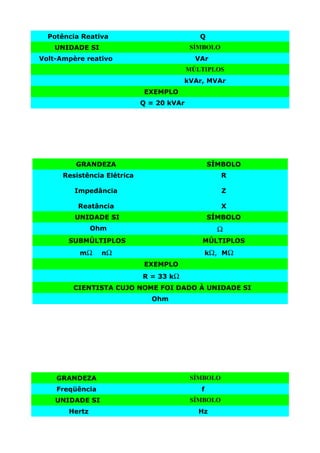
1) O documento apresenta conceitos básicos de eletricidade como potências de base 10, múltiplos e submúltiplos de unidades, e grandezas elétricas como tensão, corrente, potência e resistência. 2) É explicado como números são representados no sistema de numeração posicional decimal através da multiplicação dos algarismos por potências de 10. 3) São mostradas as unidades e seus múltiplos/submúltiplos usados para medir grandezas elétricas como o volt, ampere, watt e oh

1. Apostila Eletricidade Básica
Disciplina: Eletricidade Básica
Professora: Engª Cátia Rosália Maroco Ortega
Curso:__________________________Módulo I
Nome:______________________________________________Nº:_____

2. ELETRICIDADE BÁSICA
POTÊNCIAS DE BASE 10
Décimos Centésimos
Centenas Dezenas Unidades Décimos Centésimos Milésimos Milionésimos
milésimos milésimos
Partes inteiras Partes decimais
10 2 10 1 10 0 10 - 1 10 - 2 10 - 3 10 - 4 10 - 5 10 - 6
Vamos ver como efetuar a transformação do número 4538
O valor deste número é formado, multiplicando-se os dígitos do número, de
trás para frente, por potências de 10, começando com 100. O último dígito
(bem à direita) é multiplicado por 10º, o penúltimo por 101, o próximo por
102 e assim por diante. o valor real do número é a soma destas multiplicações. Observe o esquema
a seguir:
4 5 3 8
Multiplica por: 103 102 101 100
ou seja: 1000 100 10 1
Resultado: 4 x 1000 5 x 100 3 x 10 8 x 1
Igual a: 4000 500 30 8
Somando tudo: 4000+500+30+8
É igual a: 4538
Observe que 4538 é exatamente:
4
(103)
milhares
5
+ (102)
centenas
3
+ (101)
dezenas
8
+ (100)
unidades

3. Ex.: 125,384
Posição ou ordem com as seguintes denominações:
Décimos Centésimos
Centenas Dezenas Unidades Décimos Centésimos Milésimos Milionésimos
milésimos milésimos
Partes inteiras Partes decimais
1 2 5 3 8 4
Partes inteiras Partes decimais
O método ao qual estamos acostumados a usar é um sistema de numeração
posicional. Isso significa que a posição ocupada por cada algarismo em um
número altera seu valor de uma potência de 10 (na base 10) para cada casa à
esquerda.
2 1 0
125 = 1x10 + 2x10 + 5x10
Base de um Sistema de Numeração
A base de um sistema é a quantidade de algarismos disponível na
representação. A base 10 é hoje a mais usualmente empregada, embora não
seja a única utilizada.
Portanto o número acima 125,380 na representação da base 10 é:
2 1 0 - 1 - 2 - 3
125,384 = 1x10 + 2x10 + 5x10 + 3x10 + 8x10 + 4x 10
= 1 x 100 + 2 x 10 + 5 x 1 + 3 x 0,1 + 8 x 0,01 + 4 x 0,001
= 100 + 20 + 5 + 0,3 + 0,08 + 0,004
= 125 + 0,384
= 125,384

4. MÚLTIPLOS E SUBMÚLTIPLOS
A fim de facilitar a compreensão de grandezas, houve a criação de múltiplos
e submúltiplos de uma unidade padrão.
Exemplos:
a - Um pacote de feijão tem 1 000 gramas. Porém é mais fácil dizer
Um Quilograma ( 1Kg), que é um múltiplo do grama.
b - Uma régua tem 0,30 m. Dizendo que ela tem 30 centímetros (cm),
entendemos mais fácil. O cm é um submúltiplo do metro.
No Sistema Elétrico é normal usarmos Potência de 10 para representar
grandezas grandes ou pequenas.
Exemplos:
Múltiplos
10 12 = 1.000.000.000.000 Tera = T
10 9 = 1.000.000.000 Giga = G
10 6 = 1.000.000 Mega = M
10 3 = 1.000 Quilo = k
10 0 = 1
Submúltiplos
10 - 3 = 0,001 mili = m
10 - 6 = 0,000001 micro = µ
10 - 9 = 0,000000001 nano = η
10 - 12 = 0,000000000001 pico = ρ

5. A tabela mostra os múltiplos e submúltiplos existentes.
Nome Símbolo Fator de multiplicação da unidade
yotta Y 1024 = 1 000 000 000 000 000 000 000 000
zetta Z 1021 = 1 000 000 000 000 000 000 000
exa E 1018 = 1 000 000 000 000 000 000
peta P 1015 = 1 000 000 000 000 000
tera T 1012 = 1 000 000 000 000
giga G 109 = 1 000 000 000
mega M 106 = 1 000 000
quilo k 10³ = 1 000
hecto h 10² = 100
deca da 10
deci d 10-1 = 0,1
centi c 10-2 = 0,01
mili m 10-3 = 0,001
micro µ 10-6 = 0,000 001
nano n 10-9 = 0,000 000 001
pico p 10-12 = 0,000 000 000 001
femto f 10-15 = 0,000 000 000 000 001
atto a 10-18 = 0,000 000 000 000 000 001
zepto z 10-21 = 0,000 000 000 000 000 000 001
yocto y 10-24 = 0,000 000 000 000 000 000 000 001
Múltiplos e Submúltiplos das unidades elétricas mais usadas
NOME SÍMBOL FATOR DE
O MULTIPLICAÇ
ÃO
Tera T 10 12
Giga G 10 9
Mega M 10 6
Quilo k 10 3
Unidade 10 0
básica
10 – 3
Mili m 10 – 6
10 – 9
Micro µ 10 – 12
Nano n
Pico p

6. Grandezas Elétricas
GRANDEZA SÍMBOLO
Tensão V
UNIDADE SI SÍMBOLO
Volt V
SUBMÚLTIPLOS MÚLTIPLOS
pV , nV , mV kV
EXEMPLO
U = 100 mV V = 2 kV
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Volta
GRANDEZA SÍMBOLO
Intensidade da I
corrente elétrica
UNIDADE SI SÍMBOLO
Ampère A
SUBMÚLTIPLOS MÚLTIPLOS
pA , nA , mA kA
EXEMPLO
I = 5 mA
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Ampère

7. GRANDEZA SÍMBOLO
Potência P
Potência Ativa
UNIDADE SI SÍMBOLO
Watt W
SUBMÚLTIPLOS MÚLTIPLOS
nW , mW kW , MW , GW , TW
EXEMPLO
P = 50 mW
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Watt
GRANDEZA SÍMBOLO
Potência Aparente S
UNIDADE SI SÍMBOLO
Volt-Ampère VA
MÚLTIPLOS
kVA, MVA, GVA
EXEMPLO
S = 225 kVA
GRANDEZA SÍMBOLO

8. Potência Reativa Q
UNIDADE SI SÍMBOLO
Volt-Ampère reativo VAr
MÚLTIPLOS
kVAr, MVAr
EXEMPLO
Q = 20 kVAr
GRANDEZA SÍMBOLO
Resistência Elétrica R
Impedância Z
Reatância X
UNIDADE SI SÍMBOLO
Ohm Ω
SUBMÚLTIPLOS MÚLTIPLOS
mΩ nΩ kΩ, MΩ
EXEMPLO
R = 33 kΩ
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Ohm
GRANDEZA SÍMBOLO
Freqüência f
UNIDADE SI SÍMBOLO
Hertz Hz

9. MÚLTIPLOS
kHz , MHz , GHz , THz
EXEMPLO
f = 30 MHz
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Hertz
GRANDEZA SÍMBOLO
Energia E
UNIDADE SI SÍMBOLO
Joule J
MÚLTIPLOS
kJ , MJ
EXEMPLO
E = 1 kJ
UNIDADE PRÁTICA SÍMBOLO
Watt-hora Wh
EQUIVALÊNCIAS
1 Wh = 3600 J
CIENTISTA CUJO NOME FOI DADO À UNIDADE SI
Joule
Exercícios
1) Escreva sob a Forma Numérica os c) 0,1 mV =
Valores em Múltiplos e Submúltiplos d) 10 kV =
do Volt. e) 0,1 kV =
a) 100 µV =
b) 350 kV =

10. 2) Escreva sob a Forma de Múltiplos
e Submúltiplos, utilizando os
Símbolos, os valores Numéricos da
Grandeza Volt a seguir respeitando
a Notação Científica.
a) 1000000 V =
b) 0,000015 V =
c) 0,001 V =
d) 0,2135 V =
e) 0,0001 V
f) 39000 V =
3) Escreva sob a Forma Numérica os
valores em Múltiplos e Submúltiplos
do Ampère.
a) 1 mA =
b) 0,1 µA =
c) 10 nA =
d) 5 KA =
e) 1000 µA =
f) 2500 pA =
4) Escreva sob a Forma de Múltiplos
e Submúltiplos os valores Numéricos
e em Potência de Dez do Ampère.
a) 0,001A =
b) 0,0001A =
c) 10 x 10–9A =
d) 20 x 10–12 A =
e) 0,000001A =
f) 150 x 103 A =

11. POTENCIAÇÃO ou EXPONENCIAÇÃO
( a ) n A letra “a” é o Número Real (base) e a Letra “n” é a Potência
ou Expoente.
Potenciação: significa multiplicar um Número Real (base) por ele
mesmo “ n” vezes.
Leitura de uma potenciação:
32 (leia-se "três elevado ao quadrado", ou "três elevado à
segunda potência" ou ainda "três elevado à dois").
Portanto neste exemplo, precisamos multiplicar o 3 por ele
mesmo duas vezes, ficando assim:
32 = 3.3 = 9 logo
33 = 3 . 3 . 3
=3.9
= 27 , então algumas outras definições podem ser utilizadas.
POTÊNCIAS COM EXPOENTES INTEIROS
Vamos recordar as definições de potências com expoentes inteiros e
bases reais.
n
( a ) = a.a.a........, se n > 2 ou n = 2 , (n vezes multiplicado)
1
( a ) =a
0
( a ) = 1, se a ≠ 0
-n
( a ) = 1 / ( a ) n , se a ≠ 0

12. PROPRIEDADES
DAS POTÊNCIAS DE EXPOENTES INTEIROS
1 - PRODUTO DE POTÊNCIAS DE MESMA BASE
Para multiplicar potências de mesma base, mantemos a base e
somamos os expoentes:
n m n+m
a .a =a
Exemplo: 2 3 . 2 2
=2 3+2
=2 5
2 - QUOCIENTE DE POTÊNCIAS DE MESMA BASE
Para dividir potências de mesma base, mantemos a base e subtraímos
os expoentes:
m n m-n
a /a =a
Exemplo: 2 5 / 2 3
=2 5-3
=2 2
3 - POTÊNCIA DE POTÊNCIA
Para elevar uma potência a um expoente, mantemos a base da
potência e multiplicamos os expoentes:
m n m.n
(a ) =a
Exemplo : ( 2 3 ) 2
=2 3.2
=2 6
4 - PRODUTO DE POTÊNCIAS DE MESMO EXPOENTE

13. Para elevar um produto a um expoente, elevamos cada fator a esse
expoente:
m m m
(a.b) =a . b
2
Exemplo : ( 2 . 10 ) = 2 2 . 10 2
5 - QUOCIENTE DE POTÊNCIAS DE MESMO EXPOENTE
Para elevar um quociente a um expoente, elevamos o dividendo e o
divisor a esse expoente:
m m m
(a / b) =a /b
Exemplo: ( 6 / 3 ) 2 = 6 2 / 3 2
Potenciação com números negativos
2 2
Observe o exemplo : (- 3 ) =9 e -3 =-9
O sinal de negativo ( - ) na frente do número três, só fará parte
da potenciação quando estiver dentro de um parêntese, caso
contrário, ele continua no seu lugar no resultado.
Porém, no primeiro exemplo, o expoente é 2, número par, por
isto o negativo do número três ao final se transforma em
positivo. Se o expoente fosse três, o resultado seria negativo:
3
(- 3 ) = (- 3 ) . (- 3 ) . (- 3 ) = 9 . (- 3 ) = - 27
3
se tirarmos os parênteses teremos, - 3 = - 3 . 3 . 3 = - 9 . 3 = - 27