(1) O documento discute propriedades termodinâmicas de sistemas simples compressíveis e substâncias puras, incluindo suas relações pressão-volume-temperatura e mudanças de fase. (2) Apresenta diagramas como p-v-T, fases, p-v e T-v para ilustrar essas propriedades e relações. (3) Explica como obter propriedades como volume específico e entalpia por meio de tabelas e interpolação linear.

1. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
Termodinâmica I
Prof. Christian Strobel
strobel@ufpr.br
Prpriedades Termodinâmicas
"Por que eu tive que nascer pai?"
-Homer J. Simpson
1 INTRODUÇÃO
O ponto de partida para quaisquer problemas termodinâmicos envolve, como já visto
no conceito de equilíbrio, as propriedades do sistema na condição inicial e final, ou na condição
de entrada e saída do sistema. Entender como estas propriedades variam, e como obtê-las, e
de extrema importância para a engenharia. Antes de prosseguir, algumas definições se fazem
importantes: o que são simtemas simples compressiveis e o que são substâncias puras.
(a) Sistemas simples compressíveis
Sistemas simples compressíveis são sistemas que consistem de substâncias simples com-
pressíveis, que por sua vez são substâncias em que os efeitos de superfície, magnéticos e elétricos
não são significativos. Por outro lado, as variações no volume, tais como aquelas associadas à
expansão de um fluido em um cilindro, por exemplo, são muito importantes.
(b) Substâncias puras
Substâncias puras são aquelas de composição química uniforme e invariável. Pode existir
em mais de uma fase, mas a composição química é a mesma em todas as fases. Às vezes uma
mistura de gases, tal como o ar, é considerada como uma substância pura, desde que não haja
mudança de fase de nenhum de seus componentes. Rigorosamente isto não é verdade, mas, como
será visto mais adiante, podemos dizer que uma mistura de gases como o ar, exibe algumas das
características de uma substância pura.
2 RELAÇÃO P-V-T
Começamos nosso estudo das propriedades de substâncias puras simples compressíveis
e das relações entre estas propriedades com a pressão, volume específico e temperatura. A
partir do conhecimento experimental, sabe-se que a temperatura e o volume específico podem
Termodinâmica I • Prof. Strobel 1

2. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
ser considerados independentes e a pressão determinada como função destes dois: p=p(T,v). O
gráfico deste tipo de função é uma superfície: a superfície p-v-T.
Figure 1: Superfície p-v-T e projeções - substância que expande quando solidifica. (a) Vista 3D. (b) Diagrama fases.
(c) Diagrama p-v.
Figure 2: Superfície p-v-T e projeções - substância que contrai quando solidifica. (a) Vista 3D. (b) Diagrama fases. (c)
Diagrama p-v.
(a) Superfície p-v-T
A Figura 1 apresenta a superfície p-v-T para uma substância que se expande durante a
solidificação, tal como a água. A Figura 2 corresponde a uma substância que se contrai durante
a solidificação, sendo que a maioria das substâncias exibe este comportamento. As coordenadas
de um ponto na superfície p-v-T representam os valores que a pressão, o volume específico e a
temperatura assumem quando a substância se encontra em equilíbrio.
As Figuras 1 e 2 apresentam regiões nas superfícies p-v-T denominadas sólido, líquido
e vapor. No interior destas regiões monofásicas, o estado termodinâmico é determinado por
quaisquer duas das seguintes propriedades: pressão, volume específico e temperatura, uma
vez que estas são independentes quando existe apenas uma fase presente. Localizadas entre as
regiões monofásicas estão às seguintes regiões bifásicas, onde duas fases coexistem em equilíbrio:
líquido-vapor, sólido-líquido e sólido-vapor.
Termodinâmica I • Prof. Strobel 2

3. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
Duas fases podem coexistir durante processos de mudança de fase, tais como vaporiza-
ção, fusão e sublimação. No interior destas regiões bifásicas, pressão e temperatura não são
independentes, ou seja, uma não pode ser modificada sem alteração da outra. No interior destas
regiões, o estado não pode ser determinado somente pela temperatura e pressão. Entretanto, o
estado pode ser estabelecido pelo volume específico e outra propriedade: pressão ou temper-
atura. Por fim, três fases podem coexistir em equilíbrio ao longo da linha denominada linha
tripla.
O estado no qual uma mudança de fase começa ou termina é denominado estado de satu-
ração. A região em formato de sino composta pelos estados bifásicos líquido-vapor é chamada de
região de saturação ou domo de vapor. As linhas que definem o contorno da região de saturação
são denominadas linhas de líquido saturado e de vapor saturado. O topo da região de saturação,
onde as linhas de líquido e de vapor saturado se encontram, é denominado ponto crítico. A
temperatura crítica, Tc de uma substância pura corresponde à temperatura máxima na qual as
fases líquida e de vapor podem coexistir em equilíbrio. A pressão no ponto crítico é chamada
de pressão crítica , Pc. O volume específico neste estado é chamado de volume específico crítico.
Valores das propriedades no ponto crítico para diversas substâncias são apresentados em tabelas
anexas a esta aula.
(b) Projeções da superfície p-v-T
(i) Diagrama de Fases
Se a superfície p-v-T é projetada sobre o plano pressão-temperatura, um diagrama de
propriedades conhecido como diagrama de fases é obtido. Como ilustrado nas figuras 1b e 2b,
quando a superfície é projetada dessa forma, as regiões bifásicas se resumem a linhas. Um ponto
em qualquer destas linhas representa todas as misturas bifásicas na temperatura e na pressão
especificadas. O termo temperatura de saturação denomina a temperatura na qual uma mudança
de fase ocorre para uma dada pressão, que, por sua vez, é denominada pressão de saturação para
a dada temperatura. Os diagramas de fase mostram que, para cada pressão de saturação, existe
uma única temperatura de saturação, e vice-versa.
A linha tripla na superfície p-v-T tridimensional é projetada em um único ponto no
diagrama de fases. Esse ponto é denominado ponto triplo (Tc da água é 273,16K/0◦C e Pc é 0,006
atm).
(ii) Diagrama p-v
Projetando a superfície p-v-T sobre o plano pressão-volume específico resulta no dia-
grama p-v, como mostrado nas figuras 1c e 2c. Durante a resolução de problemas, um esboço
deste diagrama é sempre conveniente. De forma a facilitar o uso desse esboço, deve-se chamar
a atenção para o comportamento das linhas de temperatura constante (isotermas). A partir das
figuras 1c e 2c, observa-se que, para uma temperatura inferior à do ponto crítico, a pressão se
mantém constante ao longo de uma transformação líquido-vapor. Entretanto, para as regiões
monofásicas de líquido e de vapor, a pressão diminui, para uma dada temperatura, à medida
que o volume específico aumenta. Para temperaturas iguais ou superiores à temperatura crítica,
a pressão se reduz continuamente, para uma dada temperatura, à medida que o volume especí-
Termodinâmica I • Prof. Strobel 3

4. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
fico aumenta, não havendo passagem pela região bifásica líquido-vapor. A isoterma crítica passa
por uma inflexão com inclinação nula no ponto crítico.
(iii) Diagrama T-v
Projetando as regiões de líquido, bifásica líquido-vapor e de vapor da superfície p-v-
T sobre o plano temperatura-volume específico, obtém-se um diagrama T-v como mostrado na
Figura 3. Uma vez que características semelhantes são apresentadas para o comportamento p-
v-T de todas as substâncias puras, o diagrama T-v para a água mostrado na Figura 3 pode ser
considerado como representativo.
Figure 3: Esboço de um diagrama temperatura-volume específico para a água.
3 MUDANÇA DE FASE
O estudo dos eventos que ocorrem quando uma substância pura muda de fase se torna
relevante. De início, considere um sistema fechado com massa unitária de água líquida a 20◦C
mantida no interior de um conjunto pistão cilindro, como ilustrado na Figura 4. Este estado é
representado pelo ponto 1 na Figura 3. Suponha que a água é aquecida lentamente enquanto sua
pressão é mantida constante e uniforme dentro do sistema.
Figure 4: Ilustração de uma transformação líquido-vapor para a água a pressão constante.
Termodinâmica I • Prof. Strobel 4

5. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
À medida que o sistema é aquecido a uma pressão constante, a temperatura aumenta de
forma considerável, enquanto que o volume específico apresenta uma elevação menos significa-
tiva. Eventualmente, o sistema alcança o estado representado pela letra f na Figura 3. Este é o
estado de líquido saturado correspondente à pressão especificada. Quando o sistema se encontra
neste estado, uma transferência de calor adicional à pressão constante resulta na formação de
vapor sem qualquer mudança de temperatura, mas com um significativo aumento de volume
específico. Como mostrado na Figura 4b, o sistema seria composto de uma mistura bifásica
líquido-vapor. Quando uma mistura de líquido e vapor existe em equilíbrio, a fase líquida é um
líquido saturado e a fase vapor é um vapor saturado. Se o sistema continua a ser aquecido até
que a última porção de líquido tenha sido vaporizada, ele é levado ao ponto g da Figura 3, o
estado de vapor saturado. Se calor continuasse a ser fornecido, então o sistema passaria a um
estado de vapor superaquecido.
As misturas bifásicas de líquido-vapor intermediárias podem ser distinguidas entre si
pelo seu título, que é uma propriedade intensiva. A razão entre a massa de vapor presente e a
massa total do sistema é o seu título, x. Em forma matemática, tem-se:
x =
mvapor
mlquido + mvapor
O valor do título varia de zero até a unidade: para estados de líquido saturado, x = 0,
e para estados de vapor saturado, x = 1. Muito embora definido como uma razão, o título é
geralmente expresso em porcentagem.
4 OBTENDO PROPRIEDADES TERMODINÂMICAS
Dados de propriedades termodinâmicas podem ser obtidos de várias formas, incluindo
tabelas, gráficos, equações e programas de computador, porém, utilizaremos as tabelas.
Quando a temperatura ou pressão é encontrada para um fluido no estado saturado e
esta existe na tabela, o seu uso é direto. Porém, os estados envolvidos quando da resolução
de problemas geralmente não estão contidos no conjunto de valores fornecidos pelas tabelas de
propriedades. A interpolação entre valores adjacentes da tabela torna-se então necessária.
Exemplo: Determinemos o volume específico do vapor d’água para um estado onde
p=10bar e T=215◦C. A Figura 5 mostra um conjunto de dados extraídos da Tabela A-4 (Ver
tabelas em anexo). Para a pressão de 10 bar, a temperatura especificada de 215◦C se encontra
entre os valores tabelados de 200◦C e 240◦C, que são mostrados em negrito. Os valores de volume
específico correspondentes são também mostrados em negrito.
Termodinâmica I • Prof. Strobel 5

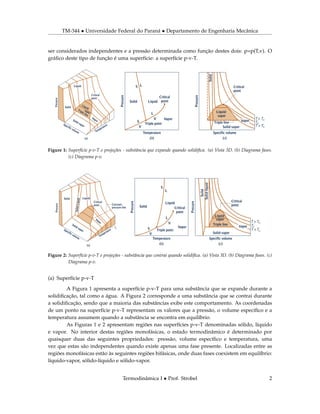
6. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
Figure 5: Ilustração da interpolação linear.
Para determinar o volume específico v correspondente a 215◦C, podemos pensar na in-
clinação de uma linha reta que une os estados adjacentes da tabela, como segue:
incl. =
(0, 2275 − 0, 2060)m3
kg
(240 − 200)◦C
=
(v − 0, 2060)m3
kg
(215 − 200)◦C
v = 0, 2141
m3
kg
(a) Volume Especifico
O volume específico de uma mistura bifásica líquido-vapor pode ser determinado pela
utilização das tabelas de saturação e pela definição de título dada pela equação descrita a seguir.
O volume total da mistura é a soma dos volumes das fases líquidas e de vapor.
V = Vliq + Vvap
Dividindo pela massa total da mistura, m, o volume específico médio para a mistura é:
v =
V
m
=
Vliq
m
+
Vvap
m
Uma vez que a fase líquida é composta por líquido saturado e que a fase vapor é com-
posta por vapor saturado, Vliq = mliq.vliq e Vvap = mvap.vvap, então:
v =
mliq
m
.vliq +
mvap
m
.vvap
Utilizando a definição de título, onde x =
mvapor
m , e notando que mliq = m − mvap, tem-se:
v = (1 − x).vliq + x.vvap
v = vls + x.(vvs − vls)[
m3
kg
]
Termodinâmica I • Prof. Strobel 6

7. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
(b) Energia interna específica, entalpia e entropia
Em diversas análises termodinâmicas, a soma da energia interna com o produto da
pressão pelo volume se faz presente. Uma vez que a soma U + pV aparece tão freqüentemente
em discussões futuras, é conveniente dar a esta combinação um nome, entalpia, e um símbolo
específico, H. Por definição,
H = U + pV[kJ]
A entalpia pode ser expressa em base mássica, ficando na forma:
h = u + pv[
kJ
kg
]
As unidades de entalpia são as mesmas utilizadas para a energia interna. São obtidos,
através das tabelas de propriedades, dados para a energia interna específica u e de entalpia
h, da mesma forma que o volume específico. A energia interna específica para uma mistura
bifásica líquido-vapor é calculada para um dado título da mesma forma que o volume específico
é calculado:
u = uls + x.(uvs − uls)[
kJ
kg
]
De forma similar, a entalpia específica de uma mistura bifásica líquido-vapor é dada em
termos do título por:
h = hls + x.(hvs − hls)[
kJ
kg
]
A entropia, por sua vez, é uma propriedade que mede o grau de desordem de um sistema,
e é comumente utilizado em análises termodinâmicas de segunda lei. De forma similar, a entropia
específica de uma mistura bifásica líquido-vapor é dada em termos do título por:
s = sls + x.(svs − sls)[
kJ
kgK
]
5 EXERCÍCIOS PROPOSTOS
1. Utilizando as tabelas para a água, determine os dados de propriedades especificadas nos
estados indicados. Para cada caso, localize o estado manualmente a partir dos esboços de
diagramas P-v e T-v.
(a) A P=3 bar, T= 240 ◦C, avalie v em m3/kg e u em kJ/kg; [superaquecido, v=0,7804
m3/kg e u=2713 kJ/kg]
(b) A P=3 bar, v=0,5 m3/kg, avalie T em ◦C e u em kJ/kg; [liquido-vapor, T=133,5 ◦C e
u=2195 kJ/kg]
(c) A T=400 ◦C, P= 10 bar, avalie v em m3/kg e h em kJ/kg; [superaquecido, v=0,3066
m3/kg e h=3264 kJ/kg]
Termodinâmica I • Prof. Strobel 7

8. TM-344 • Universidade Federal do Paraná • Departamento de Engenharia Mecânica
(d) A T=320 ◦C, v=0,03 m3/kg, avalie P em MPa e u em kJ/kg; [superaquecido, P=7,354
MPa e u=2682 kJ/kg]
(e) A P=28 MPa, T=520 ◦C, avalie v em m3/kg e h em kJ/kg; [crítico, v=0,01019 m3/kg e
h=3194 kJ/kg]
(f) A T=100 ◦C, x=60%, avalie P em bar e v em m3/kg; [liquido-vapor, P=1,013bar e
v=1,005 m3/kg]
(g) A T=10 ◦C, v=100 m3/kg, avalie P em kPa e h em kJ/kg; [liquido-vapor, P=1,228 kPa
e h=2372 kJ/kg]
(h) A P=4 MPa, T=160 ◦C, avalie v em m3/kg e u em kJ/kg; [liq. subresfriado, v=0,001099
m3/kg e u=673,2 kJ/kg]
2. Determine os valores das propriedades especificadas para cada condição a seguir.
(a) Para o R134a a T=60 ◦C e v=0,072 m3/kg, determine P (kPa) e h (kJ/kg). [P=363 kPa e
h=302,1 kJ/kg]
(b) Para a amônia a P=8bar e v=0,005 m3/kg, determine T (◦C) e u (kJ/kg). [T=17,84 ◦C e
u=285,4 kJ/kg]
(c) Para R22 a T=-10 ◦C e u = 200 kJ/kg, determine P (bar) e v (m3/kg). [P=3,8485 bar e
v=0,0574 m3/kg]
Termodinâmica I • Prof. Strobel 8