Este documento apresenta um resumo sobre índices em bancos de dados, comparando as estruturas de hash e Btree. Apresenta as definições e propriedades básicas dessas estruturas, como distribuição uniforme de valores, tratamento de colisões, grau mínimo de nós e organização linear de elementos.

1. Hash e Btree
Prof: Sergio Souza Costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
http://www.slideshare.net/skosta/presentations?order=popular
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta

3. Introdução
Banco de dados utilizam indices para
recuperação de informação.
Arquivos de índices

4. Introdução: Indexação
Objetivo:
Permitir um rápido acesso aleatório aos registros num
arquivo.
O que é um índice?
Uma estrutura de dados adicional associada ao arquivo
(tabela).

5. Introdução: Tipos de Indexação
Hash
Baseiam-se na distribuição uniforme dos valores
determinados por uma função (função de hash).
Ordenados
Baseiam-se na ordenação dos valores.
Mononível x Multinível

6. Introdução: Hash
Exemplos de hash
bucket 0
bucket 1
bucket 2
bucket de overflow para o bucket 1
bucket 3
Encadeamento (ou lista) de overflow para o bucket 3

7. Introdução: Mononível

8. Introdução: Multinível (Btree)

9. Hash
Como aproveitar as características de acesso constante de
uma estrutura de dados contigua (vetor, arranjo) ?
Pense na matrícula de alunos em uma universidade ?
Posso usá-la diretamente como um índice de um vetor ?
Como seria a complexidade de busca ? Quais problemas ?

10. Hash
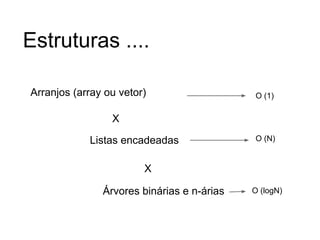
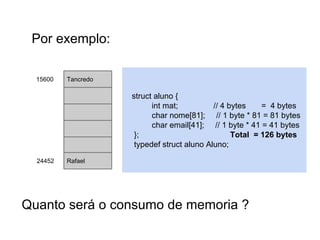
Por exemplo:
15600
Tancredo
struct aluno {
int mat;
char nome[81];
char email[41];
};
typedef struct aluno Aluno;
24452
Rafael
Quanto será o consumo de memoria ?

11. Hash
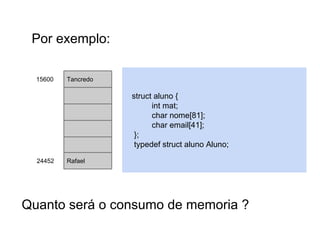
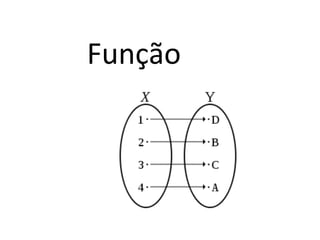
Por exemplo:
15600
Tancredo
struct aluno {
int mat;
// 4 bytes
= 4 bytes
char nome[81]; // 1 byte * 81 = 81 bytes
char email[41]; // 1 byte * 41 = 41 bytes
};
Total = 126 bytes
typedef struct aluno Aluno;
24452
Rafael
Quanto será o consumo de memoria ?

12. Hash
E se a matricula fosse composta por mais dígitos,
por exemplo 8.
E se quiséssemos indexar por outra informação,
ao invés da matricula, por exemplo o nome.

13. Função

14. Método da divisão
h(k) = k mod m
21398
17328
21513
21613
21264
Para m igual a 100, concluam o
mapeamento e me diz o que
identificaram ?
98

15. Função sobrejetora
Pode ocorrer que mais de um
"índice" seja mapeado para um único
valor.
Neste caso dizemos que ocorreu
uma "colisão".

16. Colisão
Colisão

17. Funçao hash
Função hash é como uma função qualquer, porém
o grande desafio é gerar funções onde ocorra
poucas colisões.
Em rede e sistemas operacionais vocês verão alguns
algoritmos, como o md5 e sha-1.
Como vocês acham que funciona a autenticação em
um sistem unix ?

18. Tabelas de espalhamento (Hash)
●
●
●
●
●
Hash é uma generalização da noção mais simples de um arranjo comum,
sendo uma estrutura de dados do tipo dicionário.
Dicionários são estruturas especializadas em prover as operações de
inserir, pesquisar e remover.
A idéia central do Hash é utilizar uma função, aplicada sobre parte da
informação (chave), para retornar o índice onde a informação deve ou
deveria estar armazenada.
Esta função que mapeia a chave para um índice de um arranjo é chamada
de Função de Hashing.
A estrutura de dados Hash é comumente chamada de Tabela Hash.

19. Tabelas de espalhamento (Hash)
123.456.781-00
143.576.342-23
345.365.768-93
879.094.345-45
Tabela
Hash
19
20
...
37
...
50
...
85
...
Função
de
Hashing
19
37
50
85
123.456.781-00; Fausto Silva; Av. Canal. Nº 45.
143.576.342-23; Carla Perez; Rua Celso Oliva. Nº 27.
345.365.768-93; Gugu Liberato; Av. Atlântica. S/N.
879.094.345-45 ; Hebe Camargo; Rua B. Nº 100.

20. Função Hash
●
●
●
●
●
A Função de Hashing é a responsável por gerar um índice a partir
de uma determinada chave.
O ideal é que a função forneça índices únicos para o conjunto das
chaves de entrada possíveis.
A função de Hashing é extremamente importante, pois ela é
responsável por distribuir as informações pela Tabela Hash.
A implementação da função de Hashing tem influência direta na
eficiência das operações sobre o Hash.
Tal função deve ser fácil de se computar

21. Função Hash

22. Função Hash
Considerem uma função hash que mapeia todos os
valores para o mesmo indice. Qual será a
complexidade de busca ?
Considerem uma função hash que mapeia apenas
um valor para cada indice. Qual será a
complexidade de busca?

23. Como representar ?

24. Como representar ?
Precisamos de uma função Hash

25. Como representar ?
Precisamos de uma função Hash
Precisamos de um arranjo (vetor)

26. Como representar ?
Precisamos de uma função Hash
Precisamos de um arranjo (vetor)
Precisamos tratar as colisões

27. Tratando colisões
Endereçamento fechado
Endereçamento aberto

28. Endereçamento fechado

29. Endereçamento fechado
No endereçamento fechado, a posição de inserção
não muda. Todos devem ser inseridos na mesma
posição, através de uma lista ligada em cada uma.
20 mod 5 = 0
18 mod 5 = 3
0
20
1
2
25 mod 5 = 0
colisão com 20
3
4
18
25

30. Endereçamento fechado
A busca é feita do mesmo modo: calcula-se o valor da função
hash para a chave, e a busca é feita na lista correspondente.
Se o tamanho das listas variar muito, a busca pode se tornar
ineficiente, pois a busca nas listas se torna seqüencial
0
20
4
15
11
1
2
3
0
88
32
60

31. Endereçamento fechado
A função HASH deve distribuir as chaves entre as
posições de maneira uniforme
0
1
0
15
2
3
4
5
6
10
4
13
31
88
20

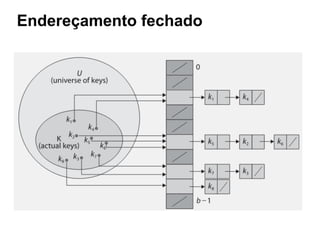
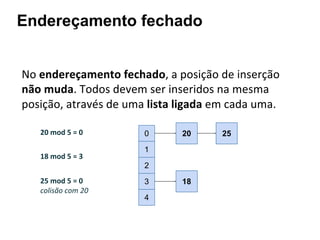
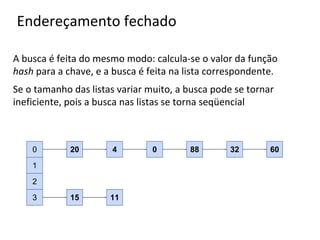
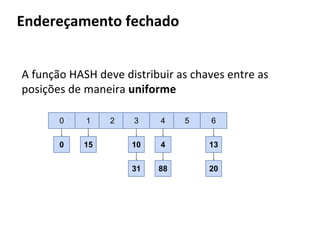
32. Endereçamento fechado
Chained-Hash-Search(T,k)
procure um elemento com chave k na lista T[h(k)] e
devolva seu ponteiro
Chained-Hash-Insert(T,x)
insira x na cabeça da lista T[h(key[x])]
Chained-Hash-Delete(T,x)
remova x da lista T[h(key[x])]

33. Atividade

34. Endereçamento aberto
No endereçamento aberto, todos os elementos são
armazenados na própria tabela hash.
Para realizar uma inserção, examinamos/testamos
sucessivamente a tabela hash ate que encontrarmos um slot
vazio no qual a chave sera inserida.
Em endereçamento aberto, a tabela hash pode encher, de forma
que não seja mais possível inserir elementos.

35. Endereçamento aberto - Inserção
0
1
9
Valores: 204, 44, 58, 10, 100, 25, 20

36. Endereçamento aberto - Inserção
Valores: 204, 44, 58, 10, 100, 25, 20
0
1
204
9

37. Endereçamento aberto - Inserção
Valores: 204, 44, 58, 10, 100, 25, 20
0
1
204
44
9

38. Endereçamento aberto - Inserção
Valores: 204, 44, 58, 10, 100, 25, 20
0
1
204
44
9
Terminem de completar ....

39. Endereçamento aberto
Algoritmo de inserção
● Usa a função hash para calcular o endereço
● Caso esteja ocupado, procure um local vazio.
● Se der uma volta completa, significa que esta cheia
Algoritmo de busca
● Usa a função hash para calcular o endereço
● Enquanto nao achar o valor procurado e nem um
espaço vazio.
● Se der uma volta completa, significa que o valor não
está lá.

40. Endereçamento aberto
Quais conclusões
que são possíveis
tirar ?
Algoritmo de inserção
● Usa a função hash para calcular o endereço
● Caso esteja ocupado, procure um local vazio.
● Se der uma volta completa, significa que esta cheia
Algoritmo de busca
● Usa a função hash para calcular o endereço
● Enquanto nao achar o valor procurado e nem um
espaço vazio.
● Se der uma volta completa, significa que o valor não
está lá.

41. Endereçamento aberto
A tabela tem que ser tratada de modo circular,
quando chega no fim da tabela a varredura
reinicia na posição 0.
Quanto mais "cheia" a tabela estiver, pior será
a eficiência.

42. Btree
Em grandes bancos de dados os índices tendem a
crescer e são armazenados em memoria secundária.
Acesso a disco não é constante.

43. Btree
Árvores de Busca Binária
Apropriada para memória principal
Ineficiente em memória secundária
Acesso: cerca de log2n
passos.
Em memoria
Em disco

44. Btree
As árvores B são árvores multicaminhos (ou multidirecionais)
balanceadas projetadas para trabalhar com dispositivos de
armazenamento secundário como discos magnéticos.
Diferente das árvores binárias, cada nó em uma árvore B pode ter
muitos filhos, isto é, o grau de um nó pode ser muito grande.
Elas visam otimizar as operações de entrada e saída nos dispositivos.
O tempo de acesso às informações em um disco é prejudicado
principalmente pelo tempo de posicionamento do braço de leitura.

45. Btree
Poucas operações de disco, 1000 chaves.
0 disk ops
1000 keys
1000
…
1001
1000
1000
…
…
…
1001
1001
1001
1000
1000
1000
…
…
1000
1 disk ops
1,001,000 keys
2 disk ops
1,002,001,000 keys

46. Btree
Árvores B têm vantagens substanciais em relação a outros tipos
de implementações quanto ao tempo de acesso e pesquisa aos
nós.
O criador das árvores B, Rudolf Bayer, não definiu claramente de
onde veio o B das árvores B.
Ao que parece, o B vem de balanceamento onde todos as folhas
da árvore estão em um mesmo nível.
Também é possível que o B tenha vindo de seu sobrenome
Bayer, ou ainda do nome da empresa onde trabalhava Boeing,
no Boeing Scientific Research Labs.

47. Btree
Árvore B é uma estrutura de dados que utiliza o recurso de
manter mais de uma chave em cada nó da estrutura.
Ela proporciona uma organização de ponteiros de tal forma
que as operações buscas, inserções e remoções são
executadas rapidamente.
As árvores B são largamente utilizadas como forma de
armazenamento em memória secundária. Diversos
sistemas comerciais de Banco de dados e sistemas de
arquivo, por exemplo, as empregam.

48. Btree: Estrutura
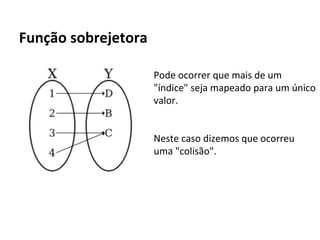
Os elementos dentro de um nó estão ordenados.
O ponteiro situado entre dois elementos a e b aponta para a
sub-árvore que contém todos os elementos entre a e b.
a
<a
b
[a,b]
c
[b,c]
>c

49. Btree: Definições (1)
1. Seja T uma árvore-B com raiz (root[T]). Ela possuirá então
as seguintes propriedades: 1. Todo o no X tem os seguintes
campos:
a. n[x], o numero de chaves atualmente guardadas no nodo x,
b. As n[x] chaves, guardadas em ordem crescente, tal que
key1[x] <= key2[x] <= … <= keyn[x]
c. leaf [x], Um valor booleano, TRUE se x e uma folha e FALSE
se x e um nodo interno
MO637 – Complexidade de Algoritmos I Arvores
B
Baseado no livro do Cormem

50. Btree: Definições (2)
2. Cada no interno x tambem contem n[x] + 1 apontadores c1[x],
c2[x],...,cn[x]+1[x] para os filhos. As folhas tem seu apontador
nulo
3. As chaves keyi[x] separam os intervalos de chaves guardadas
em cada sub-arvore: se ki e uma chave guardada numa subarvore com raiz ci[x], entao:
k1 ≤ key1[x] ≤ k2 ≤ key2[x] ≤...≤ keyn[x] ≤ kn+1
4.Todas as folhas da árvore estão no mesmo nível.
Baseado no livro do Cormem

51. Btree: Definições (3)
5. Existe um número máximo e mínimo de filhos em um nó.
Este número pode ser descrito em termos de um inteiro fixo t
maior ou igual a 2 chamado grau mínimo.
● Todo o nó diferente da raiz deve possuir pelo menos t-1 chaves. Todo
o nó interno diferente da raiz deve possuir pelo menos t filhos. Se a
árvore não é vazia, então a raiz possui pelo menos uma chave.
● Todo o nó pode conter no máximo 2t - 1 chaves. Logo um nó interno
pode ter no máximo 2t filhos. Dizemos que um nó é cheio se ele
contém 2t - 1 chaves.

52. Btree
De acordo com a definição a árvore B mais simples ocorre
quando t=2. Neste caso todo o nó diferente da raiz possui
2, 3 ou 4 filhos. Esta árvore é também conhecida
por árvore 2-3-4.

53. Grau mínimo e Ordem
Cormen não fala em Ordem, apenas em grau
mínimo t.
Diferentes definições para ordem:
● Bayer & McCreight 1972, número mínimo de chaves
● Knuth 1997, número maximo de filhos

54. Btree: Codificação
Considerando que os elementos dentro de um nó x da
B-tree esteja organizado de forma linear, e que:
n[x] = quantidade de chaves no nó x
keyi[x] = valor da chave do nó x na posição i
leaf[x] = retorna verdadeiro caso o nó seja folha
Operações de acesso
Disk-Read = operação de leitura do nó em disco
Disk-Write = operação de leitura do nó em disco

55. Btree: construtor

56. Btree: Busca
A busca em uma árvore B é uma função parecida com a de busca
em uma árvore de busca binária, exceto o fato de que se deve
decidir entre vários caminhos.
Como as chaves estão ordenadas, pode-se realizar uma busca
binária nos elementos de cada nó.
● Se a chave não for encontrada no nó em questão, continuase a busca nos filhos deste nó, realizando-se novamente a
busca binária.
● Caso o nó não esteja contido na árvore a busca terminará ao
encontrar um ponteiro igual a NULL.

57. Busca

58. Busca
Procedimento para pesquisa do número 13
30
40
50
10 20
348
9
11 13 17
25 28
33 36
42 45
48
52 55

59. Busca
Procedimento para pesquisa do número 55
30
10 20
3489
11 13 17
40 50
25 28
33 36
42 45 48
52 55

60. Inserção
Localizar o nó folha X onde o novo elemento deve ser inserido.
●Se o no X não estiver cheio, basta inserir.
●Se o nó X estiver cheio, realizar uma subdivisão de nós
●passar o elemento mediano de X para seu pai
●subdividir X em dois novos nós com t - 1 elementos
●inserir a nova chave
Se o pai de X também estiver cheio, repete-se recursivamente a
subdivisão acima para o pai de X
No pior caso terá que aumentar a altura da árvore B para poder
inserir o novo elemento

61. Divisão do nodo - Split

62. Divisão do nodo - Split

63. Divisão do nodo - Split
T=2

64. Inserção
È o caso onde a
árvore cresce
Insere na nova
raiz

65. Inserção

66. Exemplo (1)

67. Exemplo (2)

68. Atividade
Segundo o algoritmo do Cormen, insira os seguintes
elementos:
●Para t=2 e t = 3, insira 4,5,1,12,28,15
●Para t=2 e t = 3, insira 12, 45, 67, 8,9, 15, 17 19

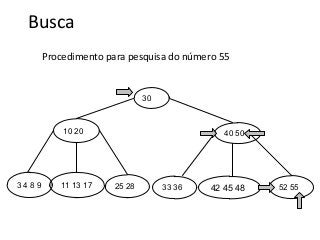
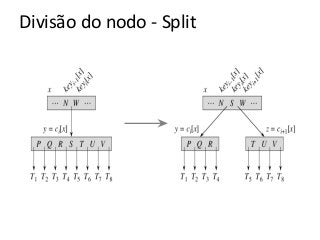
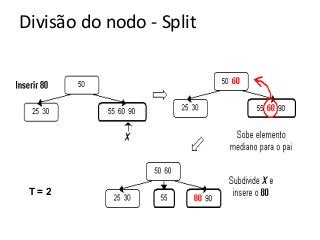
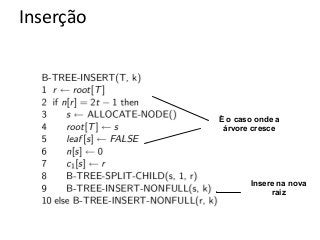
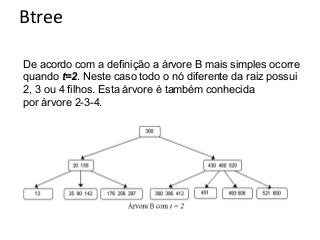
69. Atividade
A partir de uma árvore B vazia (t=2):
●Insira os seguintes valores (20,30,50,80, 12, 15)
●Agora remova o 50, 80
A partir de uma árvore B vazia (t=3)
●Insira os valores [40,60,80,90,100,20,105,12]
●Remova os valores [90,12,40,100]

70. Prática
Baixem o seguinte código, e concluem a
codificação. Usando com referencia
Cormen.

71. Referencia