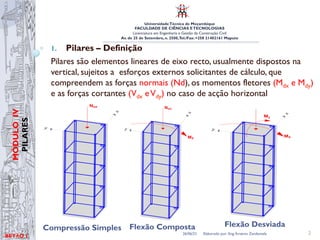
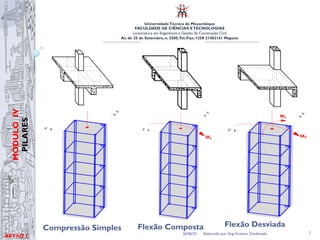
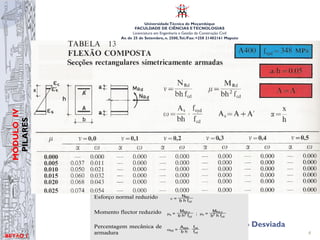
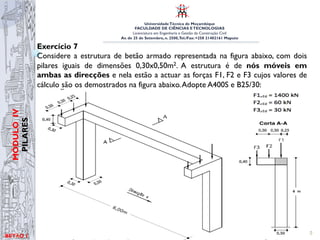
O documento aborda conceitos fundamentais na engenharia civil, focando em lajes e pilares, incluindo classificação, dimensionamento e verificação de segurança. Ele descreve os métodos de determinação de esforços em elementos estruturais, assim como as condições de esbelteza para pilares. O conteúdo é destinado a alunos da licenciatura em Engenharia e Gestão da Construção Civil na Universidade Técnica de Moçambique.

1. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
RESUMO DO MÓDULO
1.Classificação das lajes
2.Acções
3.Pré –dimensionamento
4.Compatibilizacao de Momentos Flectores
5. Verificação de segurança quanto aos estados limites
últimos
6.Lajes armadas numa e duas direcções (Czerny e
Marcus)
7.Disposições Construtivas
8.Exercícios de Aplicação
9. Bibliografia
MÓDULO
I
LAJES
26/06/21 Elaborado por: Eng.Arsénio Zandamela 1

2. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
1. Pilares – Definição
Pilares são elementos lineares de eixo recto, usualmente dispostos na
vertical, sujeitos a esforços externos solicitantes de cálculo, que
compreendem as forças normais (Nd), os momentos fletores (Mdx e Mdy)
e as forças cortantes (Vdx eVdy) no caso de acção horizontal
26/06/21 Elaborado por: Eng.Arsénio Zandamela 2
Compressão Simples Flexão Composta Flexão Desviada

3. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 Elaborado por: Eng.Arsénio Zandamela 3
Compressão Simples Flexão Composta Flexão Desviada

4. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 4
Flexão Desviada
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
MRd,z) – ver figura seguinte, para aquela quantidade de armadura.
Representa-se também um corte para um dado nível de esforço axial
actuante.
Figura 9- Diagrama de interacção tridimensional Nrd, Mrdz e Mrdy
Se se repetir o processo para vários níveis de armadura obtêm-se os
diagramas de base para o dimensionamento e verificação da segurança.
De facto, como na flexão composta, podem estabelecer-se as equações de
equilíbrio através de grandezas adimensionais:
Esforço normal reduzido
Momento flector reduzido
Percentagem mecânica de
armadura
Eq. 2
Estruturas de Betão I
Se se repetir o processo para vários níveis de armadura obtêm-se os diagramas de
base para o dimensionamento e verificação da segurança. De facto, como na flexão
composta, podem estabelecer-se as equações de equilíbrio através de grandezas
adimensionais:
Esforço normal reduzido: Q =
NRd
b h fcd
Momentos flectores reduzidos: Py =
MRd,y
b h2
fcd
; Pz =
MRd,z
b2
h fcd
Percentagem mecânica de armadura Ztot =
Astot
b h
fsyd
fcd
Nas figuras que se seguem mostra-se como representando a calote tridimensional por
cortes para igual esforço axial, se podem obter valores de quantidades de armaduras
para esforços actuantes, Qsd, Py,sd e Pz,sd. Poderiam ser realizados, em alternativa,
cortes para determinadas relações PRd,y/PRd,z.
Estruturas de Betão I
As grandezas adimensionais que se definem são as seguintes:
Esforço normal reduzido: Q =
NRd
b h fcd
Momento flector reduzido: P =
MRd
b h2
fcd
Percentagem mecânica de armadura: Ztot =
Astot
b h
fyd
fcd
Refira-se que o esforço axial reduzido corresponde à relação entre as tensões
Estruturas de Betão I
Se se repetir o processo para vários níveis de armadura obtêm-se os diagramas de
base para o dimensionamento e verificação da segurança. De facto, como na flexão
composta, podem estabelecer-se as equações de equilíbrio através de grandezas
adimensionais:
Esforço normal reduzido: Q =
NRd
b h fcd
Momentos flectores reduzidos: Py =
MRd,y
b h2
fcd
; Pz =
MRd,z
b2
h fcd
Percentagem mecânica de armadura Ztot =
Astot
b h
fsyd
fcd
Estruturas de Betão I
As grandezas adimensionais que se definem são as seguintes:
Esforço normal reduzido: Q =
NRd
b h fcd
Momento flector reduzido: P =
MRd
b h2
fcd
Percentagem mecânica de armadura: Ztot =
Astot
b h
fyd
fcd
TABELA 13
FLEXÃO COMPOSTA
Secções rectangulares simetricamente armadas
_~fuE;3- .
{fE~' h
I ':l atB~
dEs W atQ
+--JL+
NRd
V= bh foo
MRd
J1 = bh 2 foo ~
As fSYd
OJ=bh' foo
As=A+A'
x
(X=-
h
J1 v =0,0 v=0,1 v = 0,2 v = 0,3 v= 0,4 v= 0,5
(X OJ (X OJ (X OJ '(X OJ (X OJ (X OJ
0.000 0.000 0.000 0.000 0.000 0.000 0.000
0.005 0.037 0.011 0.000 0.000 0.000 0.000 0.000
0.010 0.050 0.021 0.000 0.000 0.000 0.000 0.000
0.015 0.060 0.032 0.000 0.000 0.000 0.000 0.000
0.020 0.068 0.043 0.000 0.000 0.000 0.000 0.000
0.025 0.074 0.054 0.000 0.000 0.000 0.000 0.000
0.030 0.080 0.065 0.000 0.000 0.000 0.000 0.000
0.035 0.085 0.077 0.000 0.000 0.000 0.000 0.000
0.040 0.089 0.088 0.000 0.000 0.000 0.000 0.000
0.045 0.093 0.099 0.170 0.003 0.000 0.000 0.000 0.000
0.050 0.097 0.110 0.171 0.014 0.000 0.000 0.000 0.000
0.055 0.100 0.121 0.171 0.026 0.000 0.000 0.000 - 0.000
0.060 0.103 0.132 0.172 0.037 0.000 0.000 0.000 0.000

5. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 5
3. Comportamento de elementos esbeltos
índice de esbelteza é a razão entre o comprimento de flambagem e o raio
de giração, nas direções a serem consideradas
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
eza de um pilar é dada por:
! =
!!
!
!
Eq. 3
o comprimento efectivo da encurvadura1
(distância entre
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
! =
!
!
!
Eq. 4

6. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 6
3. Comportamento de elementos esbeltos
Dispensada a análise do pilar face a encurvadura se for respeitas as
seguintes condições (artigo 61.4 REBAP)
NOTA: Em caso algum a esbelteza deve ser superior a 140 (artigo 64º)
Quanto maior for a esbelteza maior é a sensibilidade aos efeitos da
influência do esforço axial nos esforços de flexão, apresentando-se,
seguidamente, a avaliação do comprimento de encurvadura, para casos
tipo de condições de fronteira.
Conforme o disposto no artigo 61.4o
do REBAP é dispensada a análise
do pilar face a encurvadura se for respeitas as seguintes condições:
!!
!!
≥ 3,5. ℎ!!!!!!!!!!#!! ≤ 70!
!!
!!
≥ 3,5. ℎ!
!
70
!!!#!! 70
E
É igualmente dispensada a verificação face a encurvadura no caso da
esbelteza do pilar for menor ou igual a 35 (tanta para nos fixos ou
móveis) e que esbelteza a seguinte condição.
! ≤ 50 − 15
!!,!
!!,!
!!!#!! 70
E
seguidamente, a avaliação do comprimento de encurvadura, para casos
tipo de condições de fronteira.
Conforme o disposto no artigo 61.4o
do REBAP é dispensada a análise
do pilar face a encurvadura se for respeitas as seguintes condições:
!!
!!
≥ 3,5. ℎ!!!!!!!!!!#!! ≤ 70!
!!
!!
≥ 3,5. ℎ!
!
70
!!!#!! 70
Eq.
É igualmente dispensada a verificação face a encurvadura no caso da
esbelteza do pilar for menor ou igual a 35 (tanta para nos fixos ou
móveis) e que esbelteza a seguinte condição.
! ≤ 50 − 15
!!,!
!!,!
!!!#!! 70
Eq.
Os pilares, em caso algum, devem ser esbelteza superior a 140,
considerar é o referente ao eixo perpendicular ao plano de encurvadura.
Quanto maior for a esbelteza maior é a sensibilidade aos efeitos da
influência do esforço axial nos esforços de flexão, apresentando-se,
seguidamente, a avaliação do comprimento de encurvadura, para casos
tipo de condições de fronteira.
Conforme o disposto no artigo 61.4o
do REBAP é dispensada a análise
do pilar face a encurvadura se for respeitas as seguintes condições:
!!
!!
≥ 3,5. ℎ!!!!!!!!!!#!! ≤ 70!
!!
!!
≥ 3,5. ℎ!
!
70
!!!#!! 70
Eq. 5
É igualmente dispensada a verificação face a encurvadura no caso da
esbelteza do pilar for menor ou igual a 35 (tanta para nos fixos ou
móveis) e que esbelteza a seguinte condição.
! ≤ 50 − 15
!!,!
!!,!
!!!#!! 70
Eq. 6
Os pilares, em caso algum, devem ser esbelteza superior a 140,

7. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 7
3. Comportamento de elementos esbeltos
Métodos de dimensionamento a partir dos resultados de uma análise linear de 1a
ordem
Métodos de dimensionamento a partir dos resultados de uma análise linear de 2a
ordem (acidentais e de fluência)
Módulo 4 – Pilares
Elaborado por: Arsénio Zandamela
Figura 12- Excentricidade tento em conta os efeitos de 2a
ordem
3.1 Considerações de efeitos de 2a
ordem
3.1.1 Estruturas correntes (edifícios, em geral)
Métodos de dimensionamento a partir dos resultados de uma an
linear de 1a
ordem, corrigindo a excentricidade para ter em con
efeitos de 2a ordem. (Método das excentricidades adicionais - RE
EC2).
Figura 13- Excentricidade tento em conta os efeitos de 2a
ordem
3.1.2 Determinação da excentricidade de 2a
ordem.
A excentricidade de 2a
ordem destina-se a ter em conta a deform
Módulo 5 – Pilares
Elaborado por: Arsénio Zandamela
Figura 9- Excentricidade tento em conta os efeitos de 2a
ordem
3.1 Considerações de efeitos de 2a
ordem
3.1.1 Estruturas correntes (edifícios, em geral)
Métodos de dimensionamento a partir dos resultados de uma
linear de 1a
ordem, corrigindo a excentricidade para ter em c
efeitos de 2a ordem. (Método das excentricidades adicionais - R
EC2).
Figura 10- Excentricidade tento em conta os efeitos de 2a
ordem
3.1.2 Determinação da excentricidade de 2a
ordem.
A excentricidade de 2a
ordem destina-se a ter em conta a defor
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
culo das restantes excentricidades (acidentais e de fluência)
xcentricidade Acidental (ea)
ricidade acidental destina-se a ter em conta os efeitos das
ões geométricas de execução (tolerâncias construtivas) e pode
minada através de:
!! ≥
!!
300
2!!
Eq.
12
Betão Armado e Pré-Esforçado I
s restantes excentricidades adicionais
Acidental
acidental destina-se a ter em conta os efeitos das imperfeições
xecução (tolerâncias construtivas) e pode ser determinada através de
L / 300
Betão Armado e Pré-Esforçado I
antes excentricidades adicionais
ntal
A excentricidade acidental destina-se a ter em co
imperfeições geométricas de execução (tolerâncias co
ser determinada através de:
!! ≥
!!
300
2!!
onde:
l0
- representa o comprimento efectivo de encurvadura.
3.1.3.2 Excentricidade de fluência
A excentricidade de fluência destina-se a ter em con
deformação do pilar devido aos efeitos da fluência e d
da expressão:
onde:
N , M - representam os esforços devidos às acções
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos d
geométricas de execução (tolerâncias construtivas) e pode ser determi
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de
pilar devido aos efeitos da fluência e determina-se através da expressã
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter
Betão Armado e
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das im
geométricas de execução (tolerâncias construtivas) e pode ser determinada
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de def
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
ser determinada através de:
!! ≥
!!
300
2!!
Eq.
12
onde:
l0
- representa o comprimento efectivo de encurvadura.
3.1.3.2 Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de
deformação do pilar devido aos efeitos da fluência e determina-se através
da expressão:
Eq. 13
onde:
Nsg
, Msg- - representam os esforços devidos às acções com carácter de
permanência (que provocam fluência), não afectados do coeficiente γf
ea -representa a excentricidade acidental
φc -representa o coeficiente de fluência (em geral, φ c = 2.5)
NE
representa a carga crítica de Euler:
Eq. 14
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de permanência
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da secção de betão)
A consideração da excentricidade de fluência só é importante para elementos muito
esbeltos (em geral despreza-se). Poderá deixar de ser considerada nos casos em que
se verifique uma das seguintes condições: Msd / Nsd ≥ 2.0 h ou λ ≤ 70.
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de permanência
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da secção de betão)
A consideração da excentricidade de fluência só é importante para elementos muito

8. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 8
3. Comportamento de elementos esbeltos
Métodos de dimensionamento a partir dos resultados de uma análise linear de 2a
ordem (acidentais e de fluência)
as restantes excentricidades (acidentais e de fluência)
ricidade Acidental (ea)
de acidental destina-se a ter em conta os efeitos das
eométricas de execução (tolerâncias construtivas) e pode
a através de:
!! ≥
!!
300
2!!
Eq.
12
comprimento efectivo de encurvadura.
ricidade de fluência
de de fluência destina-se a ter em conta o acréscimo de
Betão Armado e Pré-Esforçado I
antes excentricidades adicionais
tal
ntal destina-se a ter em conta os efeitos das imperfeições
o (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
mprimento efectivo de encurvadura.
ncia
Betão Armado e Pré-Esforçado I
excentricidades adicionais
estina-se a ter em conta os efeitos das imperfeições
râncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
ento efectivo de encurvadura.
l0
- representa o comprimento efectivo de encurvadur
3.1.3.2 Excentricidade de fluência
A excentricidade de fluência destina-se a ter em c
deformação do pilar devido aos efeitos da fluência e
da expressão:
onde:
Nsg
, Msg- - representam os esforços devidos às acçõe
permanência (que provocam fluência), não afectados
ea -representa a excentricidade acidental
φc -representa o coeficiente de fluência (em geral, φ
NE
representa a carga crítica de Euler:
ea = max
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo
pilar devido aos efeitos da fluência e determina-se através da expres
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácte
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da secçã
A consideração da excentricidade de fluência só é importante para
geométricas de execução (tolerâncias construtivas) e pode ser determina
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de d
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
EI
Módulo 4 – Pilares
Elaborado por: Arsénio Zandamela
onde:
Nsg
, Msg- - representam os esforços devido
permanência (que provocam fluência), não
ea -representa a excentricidade acidental
φc -representa o coeficiente de fluência (em
NE
representa a carga crítica de Euler:
pilar devido aos efeitos da fluência e determina-se através
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
onde
Nsg, Msg representam os esforços devidos às acções c
(que provocam fluência), não afectados do coeficiente
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc =
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (
A consideração da excentricidade de fluência só é impo
esbeltos (em geral despreza-se). Poderá deixar de ser co
se verifique uma das seguintes condições: Msd / Nsd ≥ 2.0
A excentricidade de fluência destina-se a ter em conta o acrés
pilar devido aos efeitos da fluência e determina-se através da e
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com c
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da
A consideração da excentricidade de fluência só é important
esbeltos (em geral despreza-se). Poderá deixar de ser conside
se verifique uma das seguintes condições: Msd / Nsd ≥ 2.0 h o
ser determinada através de:
!! ≥
!!
300
2!!
onde:
l0
- representa o comprimento efectivo de encurvadura.
3.1.3.2 Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo
deformação do pilar devido aos efeitos da fluência e determina-se atrav
da expressão:
onde:
Nsg
, Msg- - representam os esforços devidos às acções com carácter de
permanência (que provocam fluência), não afectados do coeficiente γf
ea -representa a excentricidade acidental
φc -representa o coeficiente de fluência (em geral, φ c = 2.5)
NE
representa a carga crítica de Euler:
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de permanência
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da secção de betão)
A consideração da excentricidade de fluência só é importante para elementos muito
esbeltos (em geral despreza-se). Poderá deixar de ser considerada nos casos em que
se verifique uma das seguintes condições: Msd / Nsd ≥ 2.0 h ou λ ≤ 70.
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de permanência
(que provocam fluência), não afectados do coeficiente γf
ea representa a excentricidade acidental
ϕc representa o coeficiente de fluência (em geral, ϕc = 2.5)
NE representa a carga crítica de Euler NE = 10
EI
L0
2 (EI da secção de betão)
A consideração da excentricidade de fluência só é importante para elementos muito
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
3.1.3 Cálculo das restantes excentricidades (acidentais e de fluência)
3.1.3.1 Excentricidade Acidental (ea)
A excentricidade acidental destina-se a ter em conta os efeitos das
imperfeições geométricas de execução (tolerâncias construtivas) e pode
ser determinada através de:
!! ≥
!!
300
2!!
Eq.
12
onde:
l0
- representa o comprimento efectivo de encurvadura.
3.1.3.2 Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de
deformação do pilar devido aos efeitos da fluência e determina-se através
da expressão:
Eq. 13
onde:
Nsg
, Msg- - representam os esforços devidos às acções com carácter de
Betão Armado e Pré-Esforçado I
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
onde
Nsg, Msg representam os esforços devidos às acções com carácter de permanência
(que provocam fluência), não afectados do coeficiente γ
Betão Armado e Pré-Esforçado I
2.5.2. Cálculo das restantes excentricidades adicionais
1. Excentricidade Acidental
A excentricidade acidental destina-se a ter em conta os efeitos das imperfeições
geométricas de execução (tolerâncias construtivas) e pode ser determinada através de
ea = max
L0 / 300
0.02m
onde L0 representa o comprimento efectivo de encurvadura.
2. Excentricidade de fluência
A excentricidade de fluência destina-se a ter em conta o acréscimo de deformação do
pilar devido aos efeitos da fluência e determina-se através da expressão,
ec =
Msg
Nsg
+ ea exp
ϕc Nsg
NE − Nsg
− 1
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
onde (EI da secção do betão).
A consideração da excentricidade de fluência só é importante para
elementos muito esbeltos (em geral despreza-se). Poderá deixar de ser
considerada nos casos em que se verifique uma das seguintes
condições:
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
onde (EI da secção do betão).
A consideração da excentricidade de fluência só é importante para
elementos muito esbeltos (em geral despreza-se). Poderá deixar de ser
considerada nos casos em que se verifique uma das seguintes
condições:
Msd
/ Nsd
≥ 2.0 h ou λ ≤ 70. Eq. 15

9. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 9
4.Verificação de Segurança dos Estados Limites Últimos de
Encurvadura
4.1 Esforços nas secções críticas do pilar
4. Verificação de Segurança dos Estados Limites Últimos de
Encurvadura
Verificação do estado limite último de flexão composta na secção crítica
(secção mais esforçada), para os esforços e dada por:
Nsd’ = Nsd
Msd’=Msd +Nsd (ea +e2 +ec)
Eq. 16
4.1 Esforços nas secções críticas do pilar
(i) Estruturas de nós fixos
A localização da secção crítica depende do diagrama de Msd (conforme se
pode observar na figura seguinte, em geral a secção crítica localiza-se
numa zona intermédia, e não junto das extremidades).

10. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 10
5. Estruturas de pórticos
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
que garantirão a indeslocabilidade dos nós dos pilares menos rígidos.
Com essas premissas classificam-se os elementos verticais dos edifícios
em elementos de contraventamento e elementos (pilares) contraventados,
como ilustrado nas figuras abaixo.
(a)estrutura contraventada2
(b) estrutura sem contraventamento
Figura 16- Estruturas contraventadas e nao contraventadas
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
que garantirão a indeslocabilidade dos nós dos pilares menos rígidos.
Com essas premissas classificam-se os elementos verticais dos edifícios
em elementos de contraventamento e elementos (pilares) contraventados,
como ilustrado nas figuras abaixo.
(a)estrutura contraventada2
(b) estrutura sem contraventamento
Figura 16- Estruturas contraventadas e nao contraventadas

11. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 11
5. Estruturas de pórticos
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
Para nós fixo teremos: Para nós móveis teremos:
!!# =
0,7 + 0,05!(!! + !!)
0,85 + 0,05!(!!#)
1
!!# =
1 + 0,15!(!! + !!)
2 + 0,3!(!!#)
Os parâmetros α1 e α2 são relativos às extremidades 1 e 2 do pilar
que tendem a produzir maior ou menor dificuldade de rotação das
extremidades do pilar:
Eq. 20
Betão Armado e Pré-Esforçado I
α1 e α2 – parâmetros relativos às extremidades 1 e 2 do pilar, dadas por:
αi =
∑( )
EI / L pilares
nó i:
viga
!!# =
0,7 + 0,05!(!! + !!)
0,85 + 0,05!(!!#)
1
!!# =
1 + 0,15!(!! + !!)
2 + 0,3!(!!#)
Os parâmetros α1 e α2 são relativos às extremidades 1 e 2 do pilar
que tendem a produzir maior ou menor dificuldade de rotação das
extremidades do pilar:
Eq. 20
Maior rotação ⇒ maior deformação ⇒ maiores efeitos de 2a
ordem sobre
o pilar. No entanto caso o pilar esteja ligado a fundação teremos os
seguintes cenários:
α = 1 – fundações que confiram encastramento parcial
α = 0 – fundações que confiram encastramento perfeito
Betão Armado e Pré-Esfor
α1 e α2 – parâmetros relativos às extremidades 1 e 2 do pilar, dadas por:
αi =
∑( )
EI / L pilares
∑( )
EI / L vigas
nó i:
viga
pilar
Este parâmetro pretende traduzir a maior ou menor dificuldade de rotação do nó:
Maior rotação ⇒ maior deformação ⇒ maiores efeitos de 2ª ordem.
Caso as extremidades do pilar estejam ligadas a elementos de fundação
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
Para nós fixo teremos: Para nós móveis teremos:
!!# =
0,7 + 0,05!(!! + !!)
0,85 + 0,05!(!!#)
1
!!# =
1 + 0,15!(!! + !!)
2 + 0,3!(!!#)
Os parâmetros α1 e α2 são relativos às extremidades 1 e 2 do pilar
que tendem a produzir maior ou menor dificuldade de rotação das
extremidades do pilar:
Eq. 20
Maior rotação ⇒ maior deformação ⇒ maiores efeitos de 2a
ordem sobre
Betão Armado e Pré-Esforçado I
α1 e α2 – parâmetros relativos às extremidades 1 e 2 do pilar, dadas por:
αi =
∑( )
EI / L pilares
∑( )
EI / L vigas
nó i:
viga
pilar

12. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 12
6. Exercicios de aplicacao
!!# =
0,7 + 0,05!(!! + !!)
0,85 + 0,05!(!!#)
1
!!# =
1 + 0,15!(!! + !!)
2 + 0,3!(!!#)
Os parâmetros α1 e α2 são relativos às extremidades 1 e 2 do pilar
que tendem a produzir maior ou menor dificuldade de rotação das
extremidades do pilar:
Eq. 20
Maior rotação ⇒ maior deformação ⇒ maiores efeitos de 2a
ordem sobre
o pilar. No entanto caso o pilar esteja ligado a fundação teremos os
seguintes cenários:
α = 1 – fundações que confiram encastramento parcial
α = 0 – fundações que confiram encastramento perfeito
Betão Armado e Pré-Esfor
α1 e α2 – parâmetros relativos às extremidades 1 e 2 do pilar, dadas por:
αi =
∑( )
EI / L pilares
∑( )
EI / L vigas
nó i:
viga
pilar
Este parâmetro pretende traduzir a maior ou menor dificuldade de rotação do nó:
Maior rotação ⇒ maior deformação ⇒ maiores efeitos de 2ª ordem.
Caso as extremidades do pilar estejam ligadas a elementos de fundação
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
7. Exercícios
Exercicio 1
Adopte a=0,05
Estruturas de Betão I
EXERCÍCIO 15
Considere a secção rectangular representada, sujeita a flexão composta conforme
indicado. Dimensione e pormenorize a secção.
As/2
As/2
0.30
0.50
Msd
Nsd
Nsd = -1200 kN
Msd = 150 kNm
Materiais: A400NR
C20/25
RESOLUÇÃO DO EXERCÍCIO 15
Flexão composta de secções rectangulares (Tabelas)
°
°
°
d1 # 0.05m
h = 0.50m
Ÿ
d1
h = 0.10 ; A400
Esforço normal reduzido: Q =
Nsd
b h fcd
=
-1200
0.30 u 0.50 u 13.3 u 103 = -0.60
Momento flector reduzido: P =
Msd
b h2
fcd
=
150
0.30 u 0.502
u 13.3 u 103 = 0.15
fcd 13.3 4 2
Estruturas de Betão I
EXERCÍCIO 15
Considere a secção rectangular representada, sujeita a flexão composta conforme
indicado. Dimensione e pormenorize a secção.
As/2
As/2
0.30
0.50
Msd
Nsd
Nsd = -1200 kN
Msd = 150 kNm
Materiais: A400NR
C20/25
RESOLUÇÃO DO EXERCÍCIO 15
Flexão composta de secções rectangulares (Tabelas)
°
°
°
d1 # 0.05m
h = 0.50m
Ÿ
d1
h = 0.10 ; A400
Esforço normal reduzido: Q =
Nsd
b h fcd
=
-1200
0.30 u 0.50 u 13.3 u 103 = -0.60
Momento flector reduzido: P =
Msd
b h2
fcd
=
150
0.30 u 0.502
u 13.3 u 103 = 0.15
Ztot = 0.20 Ÿ Astot = Ztot b h
fcd
fyd
= 0.20 u 0.30 u 0.50 u
13.3
348
u 104
= 11.47cm2

13. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 13
6. Exercícios de aplicação
Exercício 2
Considere um pilar com secção transversal circular com Ø 0,50m.Dimensione as
armaduras do pilar com os seguintes esforços:N-1400kN, 250kN.m.Os materiais
são: C25/30,A400NR,.Adopte a=0,05.
Considere um pilar com secção transversal circular com ‡ = 0.50 m. Dimensione as
armaduras do pilar para os seguintes esforços: Nsd = -1400kN; Msd =250 kNm
Considere os seguintes materiais: C25/30, A400NR
RESOLUÇÃO DO EXERCÍCIO 16
d1 = 0.05 Ÿ
d1
h
= 0.10
°
°
°
°
Q=
Nsd
S r2
fcd
=
-1400
S u 0.252
u 16.7 u 103 = -0.427
P =
MSd
2S r3
fcd
=
250
2 u S u 0.253
u 16.7 u 103 = 0.152
Ÿ Ztot = 0.30
Astot = Ztot u Sr2
u
fcd
fyd
= 0.30 u S u 0.252
u
16.7
348 u 104
= 28.3cm2

14. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 14
6. Exercícios de aplicação
Exercício 3
Dimensione e pormenorize a seguinte secção do pilar para os esforços de calculo
indicados na figura abaixo.
Estruturas de Betão I
EXERCÍCIO 17
Dimensione e pormenorize a seguinte secção de um pilar para os esforços de cálculo
indicados.
z
0.50
0.30
y
Nsd = -1200 kN
Msd,y = 150 kNm
Msd,z = 100 kNm
Materiais: A400
C20/25
RESOLUÇÃO DO EXERCÍCIO 17
Flexão desviada com esforço axial (Tabelas)
Msdz
Msdy
Astot/4
Q =
Nsd
b h fcd
=
-1200
0.30 u 0.50 u 13.3 u 103 = -0.60
Py =
Msdy
b h2
fcd
=
150
0.30 u 0.502
u 13.3 u 103 = 0.15
0.30
Materiais: A400
C20/25
RESOLUÇÃO DO EXERCÍCIO 17
Flexão desviada com esforço axial (Tabelas)
Msdz
Msdy
Astot/4
Q =
Nsd
b h fcd
=
-1200
0.30 u 0.50 u 13.3 u 103 = -0.60
Py =
Msdy
b h2
fcd
=
150
0.30 u 0.502
u 13.3 u 103 = 0.15
Pz =
Msdz
b2
h fcd
=
150
0.302
u 0.50 u 13.3 u 103 = 0.167
Como Pz ! Py Ÿ P1 = Pz = 0.167 e P2 = Py = 0.15
°
°
°
Q= -0.6
P1 = 0.167
P2 = 0.15
Ÿ Ztot = 0.60
Ÿ Astot = Ztot b h
fcd
fsyd
= 0.60 u 0.30 u 0.50 u
13.3
348
u 104
= 34.4cm2
0.50
0.30
y
Msd,z = 100 kNm
Materiais: A400
C20/25
RESOLUÇÃO DO EXERCÍCIO 17
Flexão desviada com esforço axial (Tabelas)
Msdz
Msdy
Astot/4
Q =
Nsd
b h fcd
=
-1200
0.30 u 0.50 u 13.3 u 103 = -0.60
Py =
Msdy
b h2
fcd
=
150
0.30 u 0.502
u 13.3 u 103 = 0.15
Pz =
Msdz
b2
h fcd
=
150
0.302
u 0.50 u 13.3 u 103 = 0.167
Como Pz ! Py Ÿ P1 = Pz = 0.167 e P2 = Py = 0.15
°
°
°
Q= -0.6
P1 = 0.167
P2 = 0.15
Ÿ Ztot = 0.60
Ÿ Astot = Ztot b h
fcd
fsyd
= 0.60 u 0.30 u 0.50 u
13.3
348 u 104
= 34.4cm2

15. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 15
6. Exercícios de aplicação
Exercício 4
Dimensione o pilar indicado sujeito aos seguintes esforços:
Betão Armado e Pré-Esforçado I
EXERCÍCIO
Dimensione o pilar indicado sujeito aos seguintes esforços:
N
H
3.00
Secção transversal
0.30
0.40
Esforços característicos: N = 800 kN; H = 20kN
Materiais: C 25/30; A 400NR
RESOLUÇÃO DO EXERCÍCIO
1. Cálculo da esbelteza
λ =
L0
i =
2 × 3.0
0.0866 = 69.3
i =
I
A =
9 × 10-4
0.30 × 0.40
= 0.0866 m; I =
bh3
12 =
0.4 × 0.33
12 = 9×10-4
m4
2. Determinação dos esforços de dimensionamento
EXERCÍCIO
Dimensione o pilar indicado sujeito aos seguintes esforços:
N
H
3.00
Secção transversal
0.30
0.40
Esforços característicos: N = 800 kN; H = 20kN
Materiais: C 25/30; A 400NR
RESOLUÇÃO DO EXERCÍCIO
1. Cálculo da esbelteza
λ =
L0
i =
2 × 3.0
0.0866 = 69.3
i =
I
A =
9 × 10-4
0.30 × 0.40
= 0.0866 m; I =
bh3
12 =
0.4 × 0.33
12 = 9×10-4
m4
2. Determinação dos esforços de dimensionamento
Nsd = 800 × 1.5 = 1200 kN; M1ª ordem
sd
= 20 × 3 × 1.5 = 90.0 kN

16. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 16
6. Exercícios de aplicação
i = A =
0.30 × 0.40
= 0.0866 m; I = 12 = 12 = 9×10 m
2. Determinação dos esforços de dimensionamento
Nsd = 800 × 1.5 = 1200 kN; M1ª ordem
sd
= 20 × 3 × 1.5 = 90.0 kN
2.1.Verificação da necessidade de consideração dos efeitos de 2ª ordem
Numa estrutura de nós móveis para dispensar a verificação da segurança à
encurvadura, é necessário verificar as seguintes condições:
Msd
Nsd
=
90
1200 = 0.075 ≥
/ 3.5 h = 3.5 × 0.3 = 1.05 e λ ≤
/ 35
⇒ os efeitos de 2ª ordem não são desprezáveis
MÓDULO 5 – Verificação da segurança aos estados limite últimos de elementos
com esforço axial não desprezável
159
Betão Armado e Pré-Esforçado I
2.2. Quantificação dos esforços de cálculo
Nsd’ = 1200kN
Msd’ = Msd + Nsd (ea + e2 + ec) = 90 + 1200 × (0.02 + 0.04 + 0) = 162kNm
(i) Cálculo da excentricidade acidental
ea = max
L0 / 300 = 6 / 300 = 0.02 m
0.02 m
⇒ ea = 0.02m
(ii) Cálculo da excentricidade de 2ª ordem
e2 =
1
r
L0
2
10 = 11.13×10-3
×
(2 × 3.0)2
10 = 0.04 m

17. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 17
6. Exercícios de aplicação
Msd’ = Msd + Nsd (ea + e2 + ec) = 90 + 1200 × (0.02 + 0.04 + 0) = 162kNm
(i) Cálculo da excentricidade acidental
ea = max
L0 / 300 = 6 / 300 = 0.02 m
0.02 m
⇒ ea = 0.02m
(ii) Cálculo da excentricidade de 2ª ordem
e2 =
1
r
L0
2
10 = 11.13×10-3
×
(2 × 3.0)2
10 = 0.04 m
1
r =
5
h × 10-3
η =
5
0.30 × 10-3
× 0.668 = 11.13 × 10-3
η =
0.4 × fcd × Ac
Nsd
=
0.4 × 16.7×103
× 0.3 × 0.4
1200 = 0.668 ≤ 1.0
(iii) Excentricidade de fluência - Desprezável dado que λ 70
3. Cálculo da armadura (flexão composta)
ν =
Nsd
b h fcd
=
-1200
0.3 × 0.4 × 16.7×103 = -0.60
µ =
Msd
b h2
fcd
=
162
0.4 × 0.32
× 16.7×103 = 0.27
⇒ ωTOT = 0.62
d1
h =
0.05
0.3 = 0.167≅ 0.15 ; A400
fcd 16.7 4 2
Msd’ = Msd + Nsd (ea + e2 + ec) = 90 + 1200 × (0.02 + 0.04 + 0) = 162kNm
(i) Cálculo da excentricidade acidental
ea = max
L0 / 300 = 6 / 300 = 0.02 m
0.02 m
⇒ ea = 0.02m
(ii) Cálculo da excentricidade de 2ª ordem
e2 =
1
r
L0
2
10 = 11.13×10-3
×
(2 × 3.0)2
10 = 0.04 m
1
r =
5
h × 10-3
η =
5
0.30 × 10-3
× 0.668 = 11.13 × 10-3
η =
0.4 × fcd × Ac
Nsd
=
0.4 × 16.7×103
× 0.3 × 0.4
1200 = 0.668 ≤ 1.0
(iii) Excentricidade de fluência - Desprezável dado que λ 70
3. Cálculo da armadura (flexão composta)
ν =
Nsd
b h fcd
=
-1200
0.3 × 0.4 × 16.7×103 = -0.60
µ =
Msd
b h2
fcd
=
162
0.4 × 0.32
× 16.7×103 = 0.27
⇒ ωTOT = 0.62
d1
h =
0.05
0.3 = 0.167≅ 0.15 ; A400
ASTOT = ωTOT × bh ×
fcd
fyd
= 0.62 × 0.30 × 0.40 ×
16.7
348 × 104
= 35.7cm2

18. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 18
Exercício 6
Para a figura abaixo, calcule o comprimento de encurvadura do pilar P1(a),P2(b) e
P3.(c).Assuma que o pilar tem a mesma secção transversal em todos os pisos.

19. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 19
Exercício 6
Para a figura abaixo, calcule o comprimento de encurvadura do pilar P1(a),P2(b) e
P3.(c).Assuma que o pilar tem a mesma secção transversal em todos os pisos.
4.00
6.00 5.00
Classificação da estrutura: Estrutura de nós móveis
α1 =
∑( )
EI / L pilares
∑( )
EI / L vigas
=
∑( )
I / L pilares
∑( )
I / L vigas
=
0.34
12 ×
1
4 +
0.34
12 ×
1
3
0.3 × 0.53
12 ×
1
6 +
0.3 × 0.43
12 ×
1
5
= 0.468
α2 =
0.34
12 ×
1
3 × 2
0.3 × 0.63
12 ×
1
6 +
0.3 × 0.53
12 ×
1
5
= 0.295
η = min
1 + 0.15 (α1 + α2) = 1 + 0.5 (0.468 + 0.295) = 1.11
2.0 + 0.3 αmin = 2 + 0.3 × 0.295 = 2.09
L0 = 3 × 1.11 = 3.33m

20. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 20
Exercício 7
Considere a estrutura de betão armado representada na figura abaixo, com dois
pilares iguais de dimensões 0,30x0,50m2. A estrutura é de nós móveis em
ambas as direcções e nela estão a actuar as forças F1, F2 e F3 cujos valores de
cálculo são os demostrados na figura abaixo.Adopte A400S e B25/30:

21. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 21
Exercício 7
Considere a seguinte informação adicional:
- Na direcção do pórtico (dir. x), os pilares
encontram-se sujeitos à acção dos momentos
flectores que estão representados na figura ao
lado.
- As fundações são de grandes dimensões,
conferindo aos pilares encastramento perfeito;
- O peso próprio do pórtico é desprezável;
- Os materiais a utilizar serão o betão C25/30 e o
aço S400.
a) Determine a esbelteza do pilar em cada uma das direcções.
b) Determine as excentricidades adicionais a considerar no dimensionamento do pilar.
c) Obtenha os esforços de dimensionamento a considerar na verificação da segurança ao estado limite
último de encurvadura, localizando as respectivas secções críticas.
Determine:
a) A esbelteza do pilar em cada uma das direcções.
b) As excentricidades adicionais a considerar no dimensionamento do pilar.
c) Obtenha os esforços de dimensionamento a considerar na verificação da segurança ao estado limite
último de encurvadura, localizando as respectivas secções críticas.
d) Calcule a armadura corrente do pilar e represente-a numa secção transversal. Justifique
convenientemente todas as opções tomadas.
e) Faca o desenho esquemático do pilar

22. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 22
Exercício 7
I.Verificação de dispensa do ELU de encurvadura (nos móveis do pilar) na
direcção x: Materiais: A400S (fsyd=348.103Kpa) e B25/30 (fcd=16,7Kpa)
07
RESOLUÇÃO DO EXERCÍCIO
Alínea a)
• Direcção x – nós móveis Pilar



=
=
m
0,30
h
m
0,50
b
Fundação: encastramento perfeito ⇒ α1 = 0
0,6328
6
x
2
1
0,40
x
0,50
4
x
2
1
0,30
x
0,50
α 3
3
2 =
=



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
N
Ed
M




=
=
=
=
=
⇒




≥
≤



=
=
⇒



=
=
⇒
MPa
348
f
MPa
400
f
S400
Aço
MPa
16,7
f
MPa
25
f
C25/30
Betão
:
Materiais
yd
yk
cd
ck
Alínea a)
• Direcção x – nós móveis Pilar



=
=
m
0,30
h
m
0,50
b
Fundação: encastramento perfeito ⇒ α1 = 0
0,6328
6
x
2
1
0,40
x
0,50
4
x
2
1
0,30
x
0,50
α 3
3
2 =
=



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x



=
=
⇒



=
=
⇒
MPa
348
f
MPa
400
f
S400
Aço
MPa
16,7
f
MPa
25
f
C25/30
Betão
:
Materiais
yd
yk
cd
ck

23. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 23
Exercício 7
NOTA: Como é visível na direção x, não dispensa a verificação da encurvadura do
pilar pois os valores não satisfazem o estabelecido no REBAP no seu artigo 64.3º
II.Verificação de dispensa do ELU de encurvadura (nos móveis do pilar) na
direcção y:
Na direcção y estamos perante uma situação ilustrada na figura abaixo
Estruturas de Betão I
Elementos contraventados
Elementos não contraventados
11.3 Imperfeições geométricas
O efeito desfavorável de possíveis desvios na geometria da estrutura ou posição do
carregamento deverá ser tido em consideração no dimensionamento.
Os efeitos das imperfeições geométricas poderão ser avaliados de forma geral
considerando a estrutura inclinada de um ângulo Ti.
Para elementos isolados, estes efeitos poderão ser considerados de forma
simplificada através de uma excentricidade inicial ei ou através de uma força horizontal
equivalente Hi.
= L/2
= L
l0
l0
l0
= 0.7L
= 2L = L = 2L
l0 l0
l0
versão 0 43

 =
+
=
+
= 2,0
0
x
0,3
2,0
α
0,3
2,0
η min
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
versão 0 43 EXERC
0
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
O valor de Msd = 30x1+60x0,5+1400x0=60KN.m
Estruturas de Betão I
Elementos contraventados
Elementos não contraventados
11.3 Imperfeições geométricas
O efeito desfavorável de possíveis desvios na geometria da estrutura ou posição do
carregamento deverá ser tido em consideração no dimensionamento.
Os efeitos das imperfeições geométricas poderão ser avaliados de forma geral
considerando a estrutura inclinada de um ângulo Ti.
Para elementos isolados, estes efeitos poderão ser considerados de forma
simplificada através de uma excentricidade inicial ei ou através de uma força horizontal
equivalente Hi.
= L/2
= L
l0
l0
l0
= 0.7L
= 2L = L = 2L
l0 l0
l0
versão 0 43 EX
6
x
2
1



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
versão 0 43 EX
6
x
2
1



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)

24. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 24
Exercício 7
NOTA: Como é visível na direção x, não dispensa a verificação da encurvadura do
pilar pois os valores não satisfazem o estabelecido no REBAP no seu artigo 64.3º
II.Verificação de dispensa do ELU de encurvadura (nos móveis do pilar) na
direcção y:
Na direcção y estamos perante uma situação ilustrada na figura abaixo
versão 0 43

 =
+
=
+
= 2,0
0
x
0,3
2,0
α
0,3
2,0
η min
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
versão 0 43 EXERCÍCIO 7
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
UNIVERSIDADE TÉCNICA DE MOÇAMBIQUE
FACULDADE DE ENGENHARIAS
DEPARTAMENTO DE ENGENHARIA CIVIL
O valor de Msd = 30x1+60x0,5+1400x0=60KN.m
Estruturas de Betão I
Elementos contraventados
Elementos não contraventados
11.3 Imperfeições geométricas
O efeito desfavorável de possíveis desvios na geometria da estrutura ou posição do
carregamento deverá ser tido em consideração no dimensionamento.
Os efeitos das imperfeições geométricas poderão ser avaliados de forma geral
considerando a estrutura inclinada de um ângulo Ti.
Para elementos isolados, estes efeitos poderão ser considerados de forma
= L/2
= L
l0
l0
l0
= 0.7L
= 2L = L = 2L
l0 l0
l0
6
x
2
1
0,40
x
0,50 3
2



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)
versão 0 43 EXERCÍCIO 7
0,6328
6
x
2
1
0,40
x
0,50
α 3
2 =
=



=
+
=
+
=
⇐
=
+
=
+
+
=
2,0
0
x
0,3
2,0
α
0,3
2,0
η
nte
condiciona
1,09492
0,6328
x
0,15
1
)
α
(α
0,15
1,0
η
de
menor
min
2
1
η
l0 = η l = 1,09492 x 4 = 4,38 m
λ = 50,57
12
x
0,30
4,38
12
h
l
i
l 0
0 =
=
=
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,05
0,30
x
3,5
h
3,5
0,017
1490
25
N
M
35
50,57
λ
h
3,5
35
λ
Ed
Ed
Ed
N
Ed
M





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ex = eax + e2x
• Direcção y – nós móveis Pilar



=
=
m
0,50
h
m
0,30
b
l0 = 2 l = 2 x 4 = 8 m
λ = 55,43
12
x
0,50
8
12
h
l
i
l 0
0 =
=
= 35 ⇒ calcular as excentricidades adicionais
Condições para dispensa da verificação do E. L. U. Encurvadura (nós móveis)
1,75
0,50
x
3,5
h
3,5
0,040
1490
60
Ed
N
Ed
M
35
55,43
λ
h
3,5
N
M
35
λ
Ed
Ed





=
=
=
=
=
⇒





≥
≤
⇒ calcular as excentricidades adicionais: ey = eay + e2y
MEd = 30 x 1 + 60 x 0,50 = 60 kNm (ver alínea c)

25. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 25
Exercício 7
RESOLUÇÃO DA ALÍNEA B) DO EXERCÍCIO
Calculo das excentricidades adicionais excentricidade acidental e excentricidade de 2 ordem
e de fluência.Para tal teremos:
Verificação as excentricidades na direcção x:
I
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
DEPARTAMENTO DE ENGENHARIA CIVIL
Alínea b)
• Direcção x - excentricidades adicionais: ex = eax + e2x
⇒ m
0,02
e
m
0,0146
300
4,38
e ax
ax =
⇒
=
=
Excentricidade de 2ª ordem: 1
N
Ac
f
0,4
η
η
10
x
h
5
r
1
10
l
r
1
e
Ed
cd
3
-
2
0
2x ≤
=
=
=
67248
,
0
1490
0,50
x
0,30
x
10
x
16,7
x
0,4
η
1
N
Ac
f
0,4
η
3
Ed
cd =
=
⇒
≤
=
0,67248
x
10
x
0,30
5
r
1
η
10
x
h
5
r
1 -3
-3 =
⇒
=
m
0,0215
e
10
4,38
x
0,67248
x
10
x
0,30
5
10
l
r
1
e 2x
2
3
-
2
0
2x =
⇒
=
=
ex = eax + e2x = 0,02 + 0,0215 ⇒ ex = 0,0415 m
• Direcção y - excentricidades adicionais: ey = eay + e2y
⇒ m
0,00267
ay
e
300
8
ay
e =
= ⇒
Excentricidade acidental: cm
2
300
l
e 0
ax ≥
=
Excentricidade acidental: cm
2
l
e 0
ay ≥
=

26. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 26
Exercício 7
RESOLUÇÃO DA ALÍNEA B) DO EXERCÍCIO
Calculo das excentricidades adicionais excentricidade acidental e excentricidade de 2 ordem
e de fluência.Para tal teremos:
Verificação as excentricidades na direcção y:
m
0,0215
e
10
4,38
x
0,67248
x
10
x
0,30
5
10
l
r
1
e 2x
2
3
-
2
0
2x =
⇒
=
=
ex = eax + e2x = 0,02 + 0,0215 ⇒ ex = 0,0415 m
• Direcção y - excentricidades adicionais: ey = eay + e2y
⇒ m
0,00267
ay
e
300
8
ay
e =
= ⇒
Excentricidade de 2ª ordem: 1
N
Ac
f
0,4
η
η
10
x
h
5
r
1
10
l
r
1
e
Ed
cd
3
-
2
0
2Y ≤
=
=
=
67248
,
0
η
1
N
Ac
f
0,4
η
Ed
cd
=
⇒
≤
=
0,67248
x
10
x
0,50
5
r
1
η
10
x
h
5
r
1 -3
-3 =
⇒
=
m
0,0430
e
10
8
x
0,67248
x
10
x
0,50
5
10
l
r
1
e 2y
2
3
-
2
0
2y =
⇒
=
=
Excentricidade acidental: cm
2
300
l
e 0
ay ≥
=
m
0,0215
e
10
4,38
x
0,67248
x
10
x
0,30
5
10
l
r
1
e 2x
2
3
-
2
0
2x =
⇒
=
=
ex = eax + e2x = 0,02 + 0,0215 ⇒ ex = 0,0415 m
• Direcção y - excentricidades adicionais: ey = eay + e2y
⇒ m
0,00267
ay
e
300
8
ay
e =
= ⇒
Excentricidade de 2ª ordem: 1
N
Ac
f
0,4
η
η
10
x
h
5
r
1
10
l
r
1
e
Ed
cd
3
-
2
0
2Y ≤
=
=
=
67248
,
0
η
1
N
Ac
f
0,4
η
Ed
cd
=
⇒
≤
=
0,67248
x
10
x
0,50
5
r
1
η
10
x
h
5
r
1 -3
-3 =
⇒
=
m
0,0430
e
10
8
x
0,67248
x
10
x
0,50
5
10
l
r
1
e 2y
2
3
-
2
0
2y =
⇒
=
=
Excentricidade acidental: cm
2
300
l
e 0
ay ≥
=

27. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 27
Exercício 7
RESOLUÇÃO DA ALÍNEA B) DO EXERCÍCIO
Calculo das excentricidades adicionais excentricidade acidental e excentricidade de 2 ordem
e de fluência.Para tal teremos:
Verificação as excentricidades na direcção y:
versão 0 44 EXERCÍCIO 7
Excentricidade de 2ª ordem: 1
N
Ac
f
0,4
η
η
10
x
h
5
r
1
10
l
r
1
e
Ed
cd
3
-
0
2Y ≤
=
=
=
67248
,
0
η
1
N
Ac
f
0,4
η
Ed
cd
=
⇒
≤
=
0,67248
x
10
x
0,50
5
r
1
η
10
x
h
5
r
1 -3
-3 =
⇒
=
m
0,0430
e
10
8
x
0,67248
x
10
x
0,50
5
10
l
r
1
e 2y
2
3
-
2
0
2y =
⇒
=
=
ey = eay + e2y = 0,0267 + 0,0430 ⇒ ey = 0,0697 m

28. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 28
Exercício 7
RESOLUÇÃO DA ALÍNEA C) DO EXERCÍCIO
I
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
DEPARTAMENTO DE ENGENHARIA CIVIL
Alínea c)
• Esforços iniciais (antes do cálculo da encurvadura)
Mx,Ed My,Ed
Direcção Y Direcção x
Mx,Ed = 30 x 1 + 60 x 0,50 = 60 kNm

29. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 29
Exercício 7
RESOLUÇÃO DA ALÍNEA D) DO EXERCÍCIO
Mx,Ed My,Ed
Direcção Y Direcção x
Mx,Ed = 30 x 1 + 60 x 0,50 = 60 kNm
Estrutura de nós móveis nas duas direcções ⇒ secções críticas nas extremidades dos pilares
• Esforços de dimensionamento
Menc,x = NEd x ey = 1490 x 0,0697 = 103,85 kNm
Menc,y = NEd x ex = 1490 x 0,0415 = 61,84 kNm
Extremidade superior ⇒
kNm
76,84
61,84
15
M
15
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=
Extremidade inferior ⇒
kNm
86,84
61,84
25
M
25
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=
Mx,Ed My,Ed
Direcção Y Direcção x
Mx,Ed = 30 x 1 + 60 x 0,50 = 60 kNm
Estrutura de nós móveis nas duas direcções ⇒ secções críticas nas extremidades dos pilares
• Esforços de dimensionamento
Menc,x = NEd x ey = 1490 x 0,0697 = 103,85 kNm
Menc,y = NEd x ex = 1490 x 0,0415 = 61,84 kNm
Extremidade superior ⇒
kNm
76,84
61,84
15
M
15
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=
Extremidade inferior ⇒
kNm
86,84
61,84
25
M
25
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=

30. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 30
Exercício 7
RESOLUÇÃO DA ALÍNEA E) DO EXERCÍCIO
Para o cálculo da armadura deveremos ter em considerar os esforços máximos que ocorrem
no extremo inferior do pilar.
As mínimo e máximo
I
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
DEPARTAMENTO DE ENGENHARIA CIVIL
Alínea d)
Esforços condicionantes (ext. inferior):
kNm
86,84
M
kNm
163,85
M
kN
1490
N
Ed,y
x
Ed,
Ed





=
=
=
Ábaco 5 – Flexão desviada;
Armadura igual em todas as faces;
C12-C50; S500
0,5948
10
16,7
0,50
0,30
1490
f
h
b
N
ν
3
cd
Ed
=
×
×
×
=
=
0,1308
10
16,7
0,50
0,30
163,85
f
h
b
M
μ
3
2
cd
2
x
Ed,
x =
×
×
×
=
=
0,1156
10
16,7
0,30
0,50
86,84
f
b
h
M
μ
3
2
cd
2
y
Ed,
y =
×
×
×
=
=
versão 0 45 EX
Menc,y = NEd x ex = 1490 x 0,0415 = 61,84 kNm
Extremidade superior ⇒
kNm
76,84
61,84
15
M
15
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=
Extremidade inferior ⇒
kNm
86,84
61,84
25
M
25
M
kNm
163,85
103,85
60
M
60
M
kN
1490
N
y
enc,
y
Ed,
x
enc,
x
Ed,
Ed





=
+
=
+
=
=
+
=
+
=
=
I
ESTRUTURAS DE BETÃO 2
DEPARTAMENTO DE
Alínea d)
Esforços condicionantes (ext. inferior):
M
M
1
N
Ed,y
x
Ed,
Ed




 =
Ábaco 5 – Flexão desviada;
Armadura igual em todas as faces;
C12-C50; S500
0,5948
10
16,7
0,50
0,30
1490
f
h
b
N
ν
3
cd
Ed
=
×
×
×
=
=
0,1308
10
16,7
0,50
0,30
163,85
f
h
b
M
μ
3
2
cd
2
x
Ed,
x =
×
×
×
=
=
0,1156
10
16,7
0,30
0,50
86,84
f
b
h
M
μ
3
2
cd
2
y
Ed,
y =
×
×
×
=
=
0,4
ω
0,6
ν
0,12
μ
μ
;
0,13
μ
μ
μ
μ y
2
x
1
y
x
=
⇒



=
=
=
=
=
⇒





=
≤
=
≥
⇒
=
×
×
×
=
= 2
máx
s,
2
mín
s,
2
yd
cd
tot
s,
cm
60
A
cm
4,28
A
cm
,79
28
348
7
,
16
50
,
0
30
,
0
4
,
0
f
f
.
h
.
b
.
ω
A
Armadura mínima
2
2
3
yd
Ed
cm
3,00
0,50
x
0,30
x
0,002
Ac
0,002
nte
condiciona
cm
4,28
348x10
1490
x
0,10
f
N
0,10





=
=
⇐
=
=
≥
mín
s,
A
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
Alínea d)
Esforços condicionantes (ext. inferior):
kNm
86,84
M
kNm
163,85
M
kN
1490
N
Ed,y
x
Ed,
Ed





=
=
=
Ábaco 5 – Flexão desviada;
Armadura igual em todas as faces;
C12-C50; S500
0,5948
10
16,7
0,50
0,30
1490
f
h
b
N
ν
3
cd
Ed
=
×
×
×
=
=
0,1308
10
16,7
0,50
0,30
163,85
f
h
b
M
μ
3
2
cd
2
x
Ed,
x =
×
×
×
=
=
0,1156
10
16,7
0,30
0,50
86,84
f
b
h
M
μ
3
2
cd
2
y
Ed,
y =
×
×
×
=
=
0,4
ω
0,6
ν
0,12
μ
μ
;
0,13
μ
μ
μ
μ y
2
x
1
y
x
=
⇒



=
=
=
=
=
⇒





=
≤
=
≥
⇒
=
×
×
×
=
= 2
máx
s,
2
mín
s,
2
yd
cd
tot
s,
cm
60
A
cm
4,28
A
cm
,79
28
348
7
,
16
50
,
0
30
,
0
4
,
0
f
f
.
h
.
b
.
ω
A
Armadura mínima
2
2
3
yd
Ed
cm
3,00
0,50
x
0,30
x
0,002
Ac
0,002
nte
condiciona
cm
4,28
348x10
1490
x
0,10
f
N
0,10





=
=
⇐
=
=
≥
mín
s,
A
Esforços condicion
Ábaco 5 – Flexão
Armad
C12-C5
0,5948
10
16,7
0,50
0,30
1490
f
h
b
N
ν
3
cd
Ed
=
×
×
×
=
=
0,1308
10
16,7
0,50
0,30
163,85
f
h
b
M
μ
3
2
cd
2
x
Ed,
x =
×
×
×
=
=
0,1156
10
16,7
0,30
0,50
86,84
f
b
h
M
μ
3
2
cd
2
y
Ed,
y =
×
×
×
=
=
0,6
ν
0,12
μ
μ
;
0,13
μ
μ
μ
μ y
2
x
1
y
x
⇒



=
=
=
=
=
⇒
=
×
×
×
=
= 2
yd
cd
tot
s, cm
,79
28
348
7
,
16
50
,
0
30
,
0
4
,
0
f
f
.
h
.
b
.
ω
A
Armadura mínima
2
2
3
yd
Ed
cm
3,00
0,50
x
0,30
x
0,002
Ac
0,002
cm
4,28
348x10
1490
x
0,10
f
N
0,10





=
=
⇐
=
=
≥
mín
s,
A
Armadura máxima
cm
60
0,50
x
0,30
x
0,04
Ac
0,04
A 2
máx
s, =
=
=
• Armadura longitudinal escolhida

31. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 31
Exercício 7
RESOLUÇÃO DA ALÍNEA E) DO EXERCÍCIO
As de cálculo
Cálculo de As,estibos
No entanto, o REBAP não faz nenhuma alusão da armadura nas secções criticas
(zona superior da fundação e zona inferior à viga). No entanto o EC trás algumas
considerações sobre este aspecto que passamos a citas:
Nas secções correntes
versão 0 46 EXERCÍCIO 7
2
3
yd
cm
3,00
0,50
x
0,30
x
0,002
Ac
0,002
348x10
f




=
=
≥
mín
s,
A
Armadura máxima
cm
60
0,50
x
0,30
x
0,04
Ac
0,04
A 2
máx
s, =
=
=
• Armadura longitudinal escolhida
As,tot = 28,79 cm2
⇒ As = 4Ø25 + 4Ø20 (32,20 cm2
)
Os varões de Ø25 deverão ser colocados nos cantos da secção transversal do pilar.
• Diâmetro das cintas
Diâmetro das cintas
nte
condiciona
mm
6,25
25
x
0,25
Ø
4
1
mm
6
Øc
máx
l,





⇐
=
=
≥
Øc ≥ 6,25 mm ⇒ Øc = Ø8
versão 0 46 EXERCÍCIO 7




=
≤
⇒
=
×
×
×
=
= 2
máx
s,
mín
s,
2
yd
cd
tot
s,
cm
60
A
cm
,79
28
348
7
,
16
50
,
0
30
,
0
4
,
0
f
A
Armadura mínima
2
2
3
yd
Ed
cm
3,00
0,50
x
0,30
x
0,002
Ac
0,002
nte
condiciona
cm
4,28
348x10
1490
x
0,10
f
N
0,10





=
=
⇐
=
=
≥
mín
s,
A
Armadura máxima
cm
60
0,50
x
0,30
x
0,04
Ac
0,04
A 2
máx
s, =
=
=
• Armadura longitudinal escolhida
As,tot = 28,79 cm2
⇒ As = 4Ø25 + 4Ø20 (32,20 cm2
)
Os varões de Ø25 deverão ser colocados nos cantos da secção transversal do pilar.
• Diâmetro das cintas
Diâmetro das cintas
nte
condiciona
mm
6,25
25
x
0,25
Ø
4
1
mm
6
Øc
máx
l,





⇐
=
=
≥
Øc ≥ 6,25 mm ⇒ Øc = Ø8
I
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
DEPARTAMENTO DE ENGENHARIA CIVIL
• Cintas nas secções correntes
nte
condiciona
m
0,30
mm
300
nte
condiciona
m
0,30
pilar
do
dimensão
menor
a
m
0,375
0,025
x
15
mín
l,
Ø
15
smáx





⇐
=
⇐
=
=
=
≤ ct’s Ø8//0,30

32. UniversidadeTécnica de Moçambique
FACULDADE DE CIÊNCIAS ETECNOLOGIAS
Licenciatura em Engenharia e Gestão da Construção Civil
Av. de 25 de Setembro, n. 2500,Tel./Fax: +258 21402161 Maputo
BETĀO 1
MÓDULO
IV
PILARES
26/06/21 32
Exercício 7
RESOLUÇÃO DA ALÍNEA E) DO EXERCÍCIO
Nas secções criticas
Desenho esquemático do pilar
ou
I
ESTRUTURAS DE BETÃO 2 ISABEL ALVIM TELES
DEPARTAMENTO DE ENGENHARIA CIVIL
• Cintas nas secções correntes
nte
condiciona
m
0,30
mm
300
nte
condiciona
m
0,30
pilar
do
dimensão
menor
a
m
0,375
0,025
x
15
mín
l,
Ø
15
smáx





⇐
=
⇐
=
=
=
≤ ct’s Ø8//0,30
• Cintas nas secções localizadas numa distância de 0,50 m abaixo da viga superior e acima da fundação
nte
condiciona
m
0,18
mm
180
nte
condiciona
m
0,18
m
0,30
x
0,6
pilar
dim.
menor
x
0,6
m
0,225
0,025
x
9
mín
l,
Ø
9
smáx





⇐
=
⇐
=
=
=
=
≤ ct’s Ø8//0,175
• Desenho da secção transversal do pilar
As = 4Ø25 + 4Ø20 (os Ø25 estão colocados nos cantos)
ct’s Ø8//0,30 - na secção corrente
ct’s Ø8//0,175 - em secções localizadas numa distância de 0,50 m
abaixo da viga superior e acima da fundação
• Cintas nas secções correntes
nte
condiciona
m
0,30
mm
300
nte
condiciona
m
0,30
pilar
do
dimensão
menor
a
m
0,375
0,025
x
15
mín
l,
Ø
15
smáx





⇐
=
⇐
=
=
=
≤ ct’s Ø8//0,30
• Cintas nas secções localizadas numa distância de 0,50 m abaixo da viga superior e acima da fundação
nte
condiciona
m
0,18
mm
180
nte
condiciona
m
0,18
m
0,30
x
0,6
pilar
dim.
menor
x
0,6
m
0,225
0,025
x
9
mín
l,
Ø
9
smáx





⇐
=
⇐
=
=
=
=
≤ ct’s Ø8//0,175
• Desenho da secção transversal do pilar
As = 4Ø25 + 4Ø20 (os Ø25 estão colocados nos cantos)
ct’s Ø8//0,30 - na secção corrente
ct’s Ø8//0,175 - em secções localizadas numa distância de 0,50 m
abaixo da viga superior e acima da fundação
• Outra solução
nte
condiciona
m
0,18
mm
180
nte
condiciona
m
0,18
m
0,30
x
0,6
pilar
dim.
menor
x
0,6
smáx



⇐
=
⇐
=
=
≤ ct’s Ø8//0,175
• Desenho da secção transversal do pilar
As = 4Ø25 + 4Ø20 (os Ø25 estão colocados nos cantos)
ct’s Ø8//0,30 - na secção corrente
ct’s Ø8//0,175 - em secções localizadas numa distância de 0,50 m
abaixo da viga superior e acima da fundação
• Outra solução
As = 4Ø20+8Ø16 (28,65 cm2
) ≈ As,tot = 28,79 cm2
(varões Ø20 nos cantos)
ct’s Ø6//0,24 - na secção corrente
ct’s Ø6//0,14 - em secções localizadas numa distância de 0,50 m
abaixo da viga superior e acima da fundação
O espaçamento entre as armaduras longitudinais é inferior a 30 cm.
Não são necessárias mais cintas porque todos os varões estão cintados ou a menos de 15 cm de um
varão que está cintado.