1) O documento apresenta um resumo sobre sistemas lineares, incluindo transformada de Laplace, resposta a degraus, resposta em frequência e sistemas discretos.
2) É dividido em 6 seções que cobrem introdução a sistemas lineares, transformada de Laplace, resposta a degraus, resposta em frequência, transformada de Fourier e sistemas discretos e amostrados.
3) Fornece definições e propriedades importantes sobre esses tópicos para análise e projeto de sistemas de controle.



















![2.1. Introdu¸˜o e No¸oes de Fun¸oes Complexas
ca c˜ c˜ www.das.ufsc.br/labsil 20
obten¸˜o desses modelos lineares invariantes no tempo consistem em expandir os termos
ca
n˜o lineares pela S´rie de Taylor e aproxim´-los pela parte linear da s´rie. Por exemplo,
a e a e
para a fun¸ao y(t) = sen(t) obter´
c˜ ıamos uma aproxima¸˜o linear nas vizinhan¸as da
ca c
origem que ´ dada por ylin (t) = t e ´ f´cil de verificar que a fun¸ao y(t) = sen(t) se
e e a c˜
comporta aproximadamente como ylin (t) = t para pequenos valores da vari´vel t.
a
A Transformada de Laplace ´ uma t´cnica extremamente util na solu¸ao de equa¸˜es
e e ´ c˜ co
´ atrav´s da Transformada de Laplace que
diferenciais lineares invariantes no tempo. E e
se obt´m a no¸ao de “Fun¸˜o de Transferˆncia ” de um sistema.
e c˜ ca e
A Transformada de Laplace transforma um fun¸ao da vari´vel tempo, digamos f (t),
c˜ a
numa outra fun¸˜o F (s) onde s = σ + jω ´ uma vari´vel complexa. Em determi-
ca e a
nadas condi¸˜es, as fun¸˜es f (t) e sua transformada F (s) est˜o relacionadas de forma
co co a
bi-un´
ıvoca:
Transf. Direta
f(t) LAPLACE F(s)
Transf. Inversa
Figura 2.2: Transformada direta e inversa de Laplace
¸˜
PROPRIEDADES DE FUNCOES COMPLEXAS:
Neste curso vamos nos restringir, com poucas excess˜es, ` fun¸oes complexas racionais.
o a c˜
Defini¸˜o 2.1 (Fun¸˜o Racional) Uma fun¸˜o G(s) da vari´vel complexa s = σ+jω ´
ca ca ca a e
racional se G(s) pode ser expressa como a divis˜o de dois polinˆmios da vari´vel complexa
a o a
s.
A figura abaixo ilustra uma fun¸˜o complexa G(s) em termos de suas coordenadas
ca
retangular e polar. onde |G(s)| = G2 + G2 e ∠G(s) = tan−1 Gy /Gx .
x y
Im[G(s)]
G(s) = Gx + jGy = |G(s)| ej∠G(s)
Gy
Re[G(s)]
Gx
Figura 2.3: Representa¸ao gr´fica de uma fun¸ao complexa
c˜ a c˜
• Complexo conjugado: A conjuga¸˜o complexa ´ uma opera¸ao que consiste em trocar
ca e c˜
o sinal da parte imagin´ria, se o n´mero estiver representado nas coordenadas retangu-
a u
lares, ou de forma equivalente, trocar o sinal da fase, se o n´mero estiver representado
u](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-20-320.jpg)

![2.2. Defini¸˜o e Regi˜o de Convergˆncia
ca a e www.das.ufsc.br/labsil 22
2.2 Defini¸˜o e Regi˜o de Convergˆncia
ca a e
Para uma fun¸ao f (t) com t ≥ 0, define-se Transformada de Laplace de f (t) como
c˜
sendo a fun¸˜o complexa F (s) obtida atrav´s da integral:
ca e
∞
F (s) = L[f (t)] = f (t)e−st dt (2.1)
0−
onde s = σ + jω ´ a vari´vel complexa introduzida pela transformada. Sob certas
e a
condi¸˜es (que veremos a seguir) podemos tamb´m definir a Transformada Inversa de
co e
Laplace da seguinte forma:
c+j∞
1
f (t) = L−1 [F (s)] = F (s)est ds (2.2)
2πj c−j∞
onde t ≥ 0 e c ´ um n´mero real associado ` regi˜o do plano s = σ + jω onde a fun¸˜o
e u a a ca
F (s) est´ definida. Esta regi˜o ´ chamada regi˜o de convergˆncia da Transformada de
a a e a e
Laplace . Dentro dessa regi˜o as fun¸˜es f (t) para t ≥ 0 e F (s) est˜o ligadas de maneira
a co a
biun´ıvoca, como ilustra a figura a seguir.
Trans. Direta
f (t) F (s)
t≥0 Re[s] > c
Tranf. Inversa
Figura 2.4: Rela¸ao entre f (t) e sua transformada de Laplace
c˜
Exemplo 2.4 Seja f (t) = e2t , para t ≥ 0.
∞
−1 −(s−2)t ∞
F (s) = L[f (t)] = e2t e−st dt =
e |0 −
0− s−2
−1 1 1
= [ lim e−(s−2)t − lim e−(s−2)t ] = − lim e−(s−2)t
s − 2 t→∞ t→0− s − 2 s − 2 t→∞
Note que s = σ + jω e
|e−jωt | = |cosωt + jsenωt| = 1.
Assim,
±∞ para Re[s] = σ < 2
lim e−(s−2)t = indefinido para Re[s] = σ = 2
t→∞
0 para Re[s] = σ > 2.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-22-320.jpg)
![2.2. Defini¸˜o e Regi˜o de Convergˆncia
ca a e www.das.ufsc.br/labsil 23
Logo, a Transformada de Laplace da fun¸˜o e2t , t ≥ 0 s´ est´ definida na regi˜o do
ca o a a
plano complexo definida por Re[s] > 2 e nessa regi˜o obtemos:
a
1
F (s) = L[e2t ] =
s−2
A regi˜o do plano complexo onde a Integral de Laplace est´ definida e ´ finita re-
a a e
cebe o nome de regi˜o de convergˆncia da Transformada de Laplace . Mostra-se que ao
a e
escolhermos um contorno para a integral:
c+j∞
1
F (s)est ds
2πj c−j∞
de tal forma que c > 2 (contorno dentro da regi˜o de convergˆncia) ent˜o o resultado da
a e a
integral acima ´ e2t para t ≥ 0.
e
2
Existem fun¸oes, como por exemplo et , t ≥ 0, para as quais a Transformada de Laplace
c˜
n˜o existe, isto ´, n˜o existe regi˜o de convergˆncia da Integral de Laplace. No entanto,
a e a a e
todos os sinais de interesse pr´tico s˜o transform´veis por Laplace.
a a a
A regi˜o de convergˆncia da Transformada de Laplace ´ um formalismo matem´tico
a e e a
que normalmente ´ omitido no c´lculo da transformada. No entanto ´ importante lembrar
e a e
que qualquer que seja a regi˜o de convergˆncia, as fun¸oes f (t) para t ≥ 0 e F (s) para
a e c˜
Re[s] > c est˜o relacionados de maneira biun´
a ıvoca. Os casos em que f (t) = 0 para t < 0
s˜o de interesse marginal no c´lculo da Transformada de Laplace e n˜o ser˜o considerados
a a a a
nesse curso. Uma vez obtida a transformada de Laplace F (s) podemos deduzir sua regi˜o a
de convergˆncia. Ela ´ dada pela regi˜o do plano complexo ` direita do p´lo mais ` direita
e e a a o a
da fun¸ao F (s).
c˜
Exemplo 2.5 (Exponencial real) f (t) = eat , t ≥ 0
∞
−1 −(s−a)t ∞ 1
F (s) = L[eat ] = eat e−st dt = e |0 =
0 s−a s−a
0, t < 0
Exemplo 2.6 (Degrau Unit´rio) Fun¸˜o Degrau Unit´rio u(t) =
a ca a
1, t ≥ 0
∞
−1 −st ∞ 1
L[u(t)] = 1e−st dt = e |0 = .
0 s s
(Regi˜o de Convergˆncia Re[s] > 0)
a e
0, t < 0
Exemplo 2.7 (Rampa) Fun¸˜o Rampa f (t) =
ca
At, t ≥ 0, A constante
∞ ∞ ∞
e−st ∞ Ae−st A A
L[f (t)] = A te−st dt = At | − dt = e−st dt = .
0 −s 0 0 −s s 0 s2
( udv = uv − vdu)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-23-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 24
0, t<0
Exemplo 2.8 (Sen´ide) Fun¸˜o Senoidal f (t) =
o ca
sen(ω0 t), t ≥ 0, ω0 cte
∞ ∞
ejω0 t − e−jω0 t −st
L[f (t)] = sen(ω0 t)e−st dt = e dt
0 0 2j
1 1 1 ω0
= − = 2 2
2j s − jω0 s + jω0 s + ω0
RESUMO
u(t) ↔ 1 : P´lo simples na origem. Fun¸˜o Constante no tempo.
s
o ca
1
tu(t) ↔ s2
: P´lo duplo na origem. Fun¸˜o cresce linearmente no tempo.
o ca
1
e−αt u(t) ↔ s+α : P´lo em s = −α. Cresce exponencialmente no tempo se p´lo for positivo
o o
(α < 0). Decresce exponecialmente no tempo se p´lo for negativo (α > 0). Valor
o
constante no tempo se o p´lo for na origem.
o
sen(ω0 t)u(t) ↔ s2ω0 2 : P´los complexos conjugados sobre o eixo imagin´rio (s = ±jω0 ).
+ω0
o a
Fun¸˜o oscila no tempo sem amortecimento.
ca
2.3 Propriedades
A Transformada de Laplace possui v´rias propriedades que, em geral, simplificam o
a
c´lculo da transformada se comparado com a aplica¸ao direta da defini¸ao (2.1). To-
a c˜ c˜
das as propriedades apresentadas nessa se¸˜o est˜o provadas em [1]. Por conveniˆncia
ca a e
repetiremos algumas das provas a t´
ıtulo de exerc´
ıcio.
2.3.1 Opera¸˜o Linear
ca
Sejam f1 (t) e f2 (t) duas fun¸˜es e α1 e α2 duas constantes. Ent˜o:
co a
L[α1 f1 (t) + α2 f2 (t)] = α1 L[f1 (t)] + α2 L[f2 (t)]
Prova: Utilizando a defini¸˜o (2.1) temos:
ca
∞
L[α1 f1 (t) + α2 f2 (t)] = (α1 f1 (t) + α2 f2 (t))e−st dt
0
∞ ∞
= α1 f1 (t)e−st dt + α2 f2 (t)e−st dt
0 0
= α1 L[f1 (t)] + α2 L[f2 (t)] 2](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-24-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 25
2.3.2 Fun¸˜o Transladada em Atraso
ca
Seja f (t) uma fun¸˜o, u(t) o degrau unit´rio e α uma constante. Ent˜o:
ca a a
L[f (t − α)u(t − α)] = e−αs L[f (t)]
f (t) f (t − α)u(t − α)
t t
0 0 α
Figura 2.5: Fun¸ao deslocada em atraso
c˜
Prova: Aplicando a defini¸˜o temos:
ca
∞
L[f (t − α)u(t − α)] = f (t − α)u(t − α)e−st dt
0
Definindo τ = t − α podemos rescrever a integral acima como
∞
L[f (t − α)u(t − α)] = f (τ )u(τ )e−s(τ +α) dτ
−α
∞
= e−sα f (τ )u(τ )e−sτ dτ
−α
como f (τ )u(τ ) = 0 para −α ≤ τ < 0 temos:
∞
= e−sα f (τ )u(τ )e−sτ dτ
0
∞
= e−sα f (τ )e−sτ dτ
0
= e−sα L[f (t)] 2
2.3.3 Fun¸oes Porta-deslocada e Impulso
c˜
As fun¸oes Porta-deslocada e Impulso possuem propriedades importantes no contexto
c˜
da Transformada de Laplace .
Fun¸˜o Porta-deslocada: Usaremos a nota¸ao fp (t) para representar a fun¸˜o porta-
ca c˜ ca
deslocada de ´rea unit´ria.
a a
1
t0
, 0 < t < t0
fp (t) =
0, 0 > t > t0 sendo tO uma constante](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-25-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 26
fp (t)
1
t0
t
t0
0
Figura 2.6: Fun¸˜o Porta de ´rea unit´ria
ca a a
1 1
Note que fp (t) = t0
u(t) − t0
u(t − t0 ).
Utilizando as propriedades de Linearidade e Transla¸˜o obtemos:
ca
1 1
L[fp (t)] = L u(t) − u(t − t0 )
t0 t0
1 1
= L[u(t)] − L[u(t − t0 )]
t0 t0
−t0 s
1 1 1 e
= −
t0 s t0 s
1
= (1 − e−t0 s ) 2
t0 s
Fun¸˜o Impulso: A Fun¸˜o Impulso Unit´rio que ocorre no instante t = t0 ´ repre-
ca ca a e
sentada por δ(t − t0 ) e satisfaz as seguintes condi¸˜es:
co
∞
0, ∀t = t0
δ(t − t0 ) = e δ(t − t0 )dt = 1
∞, t = t0 −∞
A Fun¸ao Impulso ´ uma abstra¸ao matem´tica e n˜o existe na pr´tica. Por´m,
c˜ e c˜ a a a e
varia¸oes bruscas de energia podem ser aproximadas pela fun¸˜o impulso. Al´m disso,
c˜ ca e
o conceito da fun¸˜o impulso ´ bastante util na diferencia¸ao de fun¸˜es descont´
ca e ´ c˜ co ınuas,
como veremos na sequˆncia.
e
Para calcular a transformada da fun¸ao impulso devemos notar que o impulso na origem
c˜
´ o caso limite da fun¸˜o porta quando t0 → 0, isto ´:
e ca e
1
δ(t) = lim [u(t) − u(t − t0 )]
t0 →0 t0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-26-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 27
Assim temos:
1
L[δ(t)] = L lim (u(t) − u(t − t0 ))
t0 →0 t0
1
= lim L (u(t) − u(t − t0 ))
t0 →0 t0
1
= lim (1 − e−t0 s )
t0 →0 t0 s
d
dt0
(1 − e−t0 s )
= d
(t s)
dt0 0
= 1 2
A Transformada do Impulso ´ uma fun¸ao constante numericamente igual a ´rea do
e c˜ a
impulso (Energia Instantˆnea). O exemplo a seguir mostra como podemos utilizar a
a
fun¸˜o impulso para representar a derivada de fun¸oes descont´
ca c˜ ınuas.
Exemplo 2.9 Seja a fun¸˜o f (t) = A para 0 < t < t0 (t0 ) dado) e nula fora desse
ca
intervalo. A derivada sessa fun¸˜o est´ definida em todos os pontos exceto em t = 0 e
ca a
t = t0 . Nesses pontos existem descontinuidades. A varia¸˜o da fun¸˜o no entorno de
ca ca
uma descontinuidade pode ser representada por um impulso de ´rea igual ao tamanho da
a
descontinuidade. A derivada de f (t) est´ indicada na figura 2.7.
a
f(t) f˙(t)
A
A δ(t)
t0 t
t 0
0 t0
−A δ(t − t0 )
Figura 2.7: Derivada de fun¸˜es descont´
co ınuas
.
2.3.4 Multiplica¸˜o de f (t) por e−αt
ca
Se L[f (t)] = F (s) ent˜o:
a
∞
−αt
L[e f (t)] = f (t)e−αt e−st dt = F (s + α)
0
Exemplo 2.10 J´ vimos que:
a
ω0
L[sen(ω0 t)u(t)] = 2
= F (s)
s2 + ω0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-27-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 28
Logo:
ω0
L[e−αt sen(ω0 t)u(t)] = 2
= F (s + α)
(s + α)2 + ω0
Note que os p´los de F (s + α) s˜o p1,2 = −α ± jω0 , onde Re[p´lo] = −α define o
o a o
decaimento exponencial do sinal f (t) e Im[p´lo] = ±ω0 define a frequˆncia de oscila¸˜o
o e ca
do sinal f (t).
2.3.5 Mudan¸a na Escala de Tempo
c
Se L[f (t)] = F (s) ent˜o:
a
L[f (t/α)] = αF (αs)
Este resultado ´ util quando se deseja analisar sinais numa escala de tempo diferente
e´
daquela em que ele ocorre na pr´tica. Pode ser o caso por exemplo de sinais muito lentos
a
ou muito r´pidos.
a
1 5
Exemplo 2.11 Dado que L[e−t u(t)] = s+1
tem-se que L[e−0,2t u(t)] = 5s+1
.
2.3.6 Teorema da Diferencia¸˜o Real
ca
De agora em diante usaremos as seguintes nota¸oes para representar derivada temporal
c˜
de uma fun¸˜o f (t):
ca
df (t) def df (t) def ˙
= ∂f (t) ou de forma equivalente = f (t) (2.3)
dt dt
d def
A nota¸ao que emprega o operador ∂ = dt ´ util no caso de derivadas de ordem ≥ 3
c˜ e ´
como a derivada de ordem 5: ∂ f (t). J´ a nota¸ao f˙(t) e f (t) s˜o comuns em livros de
5
a c˜ ¨ a
controle para expressar derivadas de ordem 1 e 2.
Com a nota¸˜o acima temos o seguinte resultado:
ca
L f˙(t) = sF (s) − f (0)
onde L[f (t)] = F (s) e f (0) = f (t)|t=0 .
Problema 2.1 Prove que L f˙(t) = sF (s) − f (0). Dica: use a integral por partes
∞ ∞
0
udv = uv|∞ −
0 0
vdu .
Quando uma fun¸ao possui descontinuidade na origem, a sua derivada temporal ir´
c˜ a
possuir um impulso na origem. Nesses casos precisamos tomar cuidado com o limite
inferior da transformada da derivada. Vamos ent˜o definir:
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-28-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 29
∞
L+ [f (t)] = f (t)e−st dt
0+
∞
L− [f (t)] = f (t)e−st dt
0−
Note que se f (t) envolve um impulso na origem ent˜o L+ [f (t)] = L− [f (t)]. Quando
a
f (t) n˜o possui impulso na origem teremos L+ [f (t)] = L− [f (t)] = L[f (t)].
a
Para o caso em que f˙(t) possui impulso na origem (f (t) possui descontinuidade na
origem) ficamos com:
L+ f˙(t) = sF (s) − f (0+ )
L− f˙(t) = sF (s) − f (0− )
Note que na defini¸˜o L+ o tempo come¸a em t = 0+ e portanto o impulso na origem
ca c
fica fora do intervalo considerado, oque n˜o nos interessa. Assim apenas a defini¸ao L− ,
a c˜
por come¸ar a contagem dos tempos em t = 0− , nos ser´ util para tratar impulsos na
c a ´
origem.
Exemplo 2.12 Seja f (t) = e−αt , para t ≥ 0. Calcule L[f˙(t)].
Solu¸˜o:
ca
f˙(t) = δ(t) − αe−αt , t ≥ 0
α s
L[f˙(t)] = 1 − =
s+α s+α
Pelo teorema da diferencia¸˜o real obtemos o mesmo resultado acima:
ca
s s
L− [f˙(t)] = sF (s) − f (0− ) = −0=
s+α s+α
Para uma derivada de ordem n temos:
L [∂ n f (t)] = sn F (s) − sn−1 f (0) − sn−2 ∂f (t)|t=0 − · · · − s∂ n−2 f (t)|t=0 − ∂ n−1 f (t)|t=0
¸˜
OBSERVACOES:
• Se a distin¸˜o entre L+ e L− for necess´ria basta substituir t = 0 por t = 0+ ou
ca a
−
t = 0 respectivamente.
• Para que L[∂ n f (t)] exista ´ preciso que todas as derivadas de f (t) de ordem inferior
e
` n existam e sejam transform´veis por Laplace.
a a
• Quando todas as condi¸˜es iniciais forem nulas ent˜o:
co a
L [∂ n f (t)] = sn F (s)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-29-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 30
ω0
Exemplo 2.13 Sabendo que L[sen(ω0 t)u(t)] = 2
s2 +ω0
podemos obter:
d sen(ω0 t)
L[cos(ω0 t)u(t)] = L u(t)
dt ω0
1 d
= L (sen(ω0 t)u(t))
ω0 dt
1
= (sF (s) − f (0))
ω0
1 s ω0
= ( 2 2
− 0)
ω0 s + ω0
s
= 2 + ω2
s 0
2.3.7 Teorema do Valor Final
Quando uma fun¸ao f (t) tende ` um valor constante em regime estacion´rio, isto ´
c˜ a a e
quando t → ∞, este valor constante pode ser diretamente obtido atrav´s do limite:
e
lim f (t) = lim sF (s)
t→∞ s→0
onde L[f (t)] = F (s). Note que quando f (t) tende ` um valor constante em regime ent˜o
a a
f˙(t) tende a zero em regime. Como toda fun¸˜o que tende a zero em regime deve possuir
ca
transformada com todos os p´los no semi-plano esquerdo conclu´
o ımos que todos os p´los
o
de L[f ˙(t)] = sF (s) devem estar no semi-plano esquerdo para que o limite acima possa ter
algum sentido. Caso contr´rio, se algum p´lo de sF (s) tem parte real nula ou positiva a
a o
fun¸˜o f (t) n˜o tende a um valor constante em regime e portanto a igualdade acima n˜o
ca a a
mais se verifica.
Exemplo 2.14 Qual ´ o valor de regime (se ele existe) da fun¸˜o f (t) cuja transformada
e ca
1
´ F (s) = s(s+1) ?
e
Solu¸˜o: Como os p´los de sF (s) n˜o possuem parte real nula nem positiva (os p´los
ca o a o
s˜o s = −1) ent˜o f (t) tende ` um valor constante em regime. E esse valor ´ dado por:
a a a e
lim f (t) = lim sF (s) = 1
t→∞ s→0
1
Para conferir o resultado note que L[(1 − e−t )u(t)] = s(s+1)
.
Problema 2.2 Calcule o valor de regime da fun¸˜o no tempo cuja transformada ´ F (s) =
ca e
1
(s−2)
. Diga se o teorema do valor final pode ser aplicado e qual ´ a fun¸˜o no tempo.
e ca
2.3.8 Teorema do Valor Inicial
Usando este teorema somos capazes de achar o valor de f (t) em t = 0+ conhecendo
apenas a transformada de f (t). Se f (t) e f˙(t) s˜o ambas transform´veis por Laplace e se
a a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-30-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 31
lims→∞ sF (s) existir ent˜o:
a
f (0+ ) = lim sF (s)
s→∞
Quando f (t) n˜o possui descontinuidade na origem f (0+ ) = f (0).
a
Problema 2.3 Encontre o valor inicial de f˙(t) dado que L[f (t)] = 2s+1
s2 +s+1
.
2.3.9 Teorema da Integra¸˜o Real
ca
Se a fun¸ao que resulta da integral
c˜ f (t)dt ´ transform´vel por Laplace ent˜o sua
e a a
transformada ´ dada por:
e
F (s) f (t)dt
L f (t)dt = + |t=0 (2.4)
s s
¸˜
OBSERVACOES:
• Se o valor inicial da integral for zero ent˜o:
a
F (s)
L f (t)dt =
s
Assim, integrar no dom´ınio do tempo ´ dividir por s no dom´
e ınio da frequˆncia.
e
Lembre que derivar no tempo ´ multiplicar por s na frequˆncia.
e e
• Quando a integral for definida note que:
t
f (t)dt = f (t)dt − f (t)dt|t=0 .
0
Sendo f (t)dt|t=0 uma constante temos com (2.4) que:
t
F (s)
L f (t)dt =
0 s
Se f (t) possui impulso na origem ent˜o deve-se especificar que a integral come¸a
a c
−
em t = 0 .
2.3.10 Teorema da Diferencia¸˜o Complexa
ca
Se f (t) ´ transform´vel por Laplace, ent˜o, exceto nos p´los de F (s) vale a seguinte
e a a o
rela¸˜o:
ca
d
L[tf (t)] = − F (s).
ds
No caso geral:
n
n n d
L[t f (t)] = (−1) F (s), n = 1, 2, . . . .
dsn](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-31-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 32
2.3.11 Integral de Convolu¸˜o
ca
Sejam f1 (t) e f2 (t) duas fun¸˜es nulas para t < 0. A Convolu¸ao dessas duas fun¸oes
co c˜ c˜
f1 (t) e f2 (t) ser´ representada pela nota¸ao f1 (t) ∗ f2 (t) e ´ definida pela integral:
a c˜ e
t
f1 (t) ∗ f2 (t) = f1 (t − τ )f2 (τ )dτ
0
Propriedades:
• f1 (t) ∗ f2 (t) = f2 (t) ∗ f1 (t)
• f1 (t) ∗ (f2 (t) + f3 (t)) = f1 (t) ∗ f2 (t) + f1 (t) ∗ f3 (t)
• L[f1 (t) ∗ f2 (t)] = L[f1 (t)]L[f2 (t)]
A ultima propriedade ´ muito importante e mostra que fazer a convolu¸ao no tempo ´
´ e c˜ e
fazer o produto das transformadas na frequˆncia.
e
Prova:
∞ t
L[f1 (t) ∗ f2 (t)] = f1 (t − τ )f2 (τ )dτ e−st dt
0 0
como f1 (t − τ ) = 0 para τ > t podemos extender o limite de integra¸ao de t para infinito.
c˜
Como t e τ s˜o vari´veis independentes podemos trocar a ordem de integra¸ao.
a a c˜
∞ ∞
= f1 (t − τ )e−s(t−τ ) dtf2 (τ )e−sτ dτ
0 0
Note que a integral interna ´ simplesmente a transformada de f1 (t) com a mudan¸a de
e c
vari´vel ξ = t − τ :
a
∞ ∞ ∞
−s(t−τ ) −sξ
f1 (t − τ )e dt = f1 (ξ)e dξ = f1 (ξ)e−sξ dξ = L[f1 (t)]
0 −τ 0
Note ainda que L[f1 (t)] ´ uma fun¸˜o complexa da vari´vel s e n˜o depende de τ . Logo
e ca a a
obtemos:
∞
L[f1 (t) ∗ f2 (t)] = L[f1 (t)]f2 (τ )e−sτ dτ
0
∞
= L[f1 (t)] f2 (τ )e−sτ dτ
0
= L[f1 (t)]L[f2 (t)] 2
Veremos mais adiante que o comportamento de todo sistema linear invariante no tempo
pode ser representado por uma integral de convolu¸ao, ou equivalentemente, pelo produto
c˜
de duas transformadas.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-32-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 33
f (t) f˙(t)
a a ...
t
0
... −aδ(t − 2)
t
−aδ(t − 1)
0 1 2
Figura 2.8: Fun¸˜o dente de serra e sua derivada
ca
Exemplo 2.15 Calcule a transformada de Laplace da fun¸˜o f (t) da figura 2.8.
ca
Solu¸˜o: Como a derivada de f (t) ´ uma fun¸˜o mais simples que f (t), veja figura 2.8,
ca e ca
iremos calcular a transformada da derivada e utilizar a rela¸˜o L[f˙(t)] = sF (s) − f (0).
ca
Tem-se ent˜o:
a ∞
f˙(t) = au(t) − aδ(t − n)
n=1
∞
L[f˙(t)] = sF (s) − f (0) = aL[u(t)] − a L[δ(t − n)]
n=1
∞
1
⇒ sF (s) = a − a e−ns L[δ(t)]
s n=1
∞
a e−ns
⇒ F (s) = 2 − a
s n=1
s
f(t)
1
a2
t
0 a 2a
1
-
a2
Figura 2.9: Fun¸˜o onda quadrada
ca
Exemplo 2.16 Calcule a transformada de Laplace da fun¸˜o f (t) da figura 2.9.
ca
Solu¸˜o: Como a fun¸˜o ´ uma soma de degraus deslocados, temos:
ca ca e
1 2 1
f (t) = 2 u(t) − 2 u(t − a) + 2 u(t − 2a)
a a a
1 2 1
L[f (t)] = 2 L[u(t)] − 2 L[u(t − a)] + 2 L[u(t − 2a)]
a a a
1 1 2 −as 1 1 −2as 1
= 2 − 2e + e
a s a s a2 s
1 −as −2as
= 2 (1 − 2e +e )
as](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-33-320.jpg)
![2.3. Propriedades www.das.ufsc.br/labsil 34
Exemplo 2.17 Calcule a transformada de Laplace da fun¸˜o x(t) que resolve a seguinte
ca
dx(t)
equa¸˜o diferencial a¨ + bx + cx = 0, onde x = dt e x(0) = k1 , x(0) = k2 .
ca x ˙ ˙ ˙
Solu¸˜o: Seja X(s) = L[x(t)]. Tomando a transformada dos dois lados da equa¸˜o
ca ca
temos:
L[a¨ + bx + cx] = L[0] = 0
x ˙
aL[¨] + bL[x] + cL[x] = 0
x ˙
L[x] = X(s)
L[x] = sX(s) − x(0)
˙
L[¨] = s2 X(s) − sx(0) − x(0)
x ˙
a[s2 X(s) − sk1 − k2 ] + b[sX(s) − k1 ] + cX(s) = 0
X(s)(as2 + bs + c) = ak1 s + bk1 + ak2
ak1 s + bk1 + ak2
X(s) =
as2 + bs + c
Exemplo 2.18 Calcule a transformada de Laplace do sinal f (t) = sen(ω0 t+θ)u(t), onde
θ e ω0 s˜o constantes.
a
Solu¸˜o: Existem v´rias formas de se resolver o problema. A seguir apresenta-se uma
ca a
forma que explora as propriedades de fun¸˜es senoidais e da fun¸˜o impulso.
co ca
f (t) = sen(ω0 t + θ)u(t)
f˙(t) = cos(ω0 t + θ)ω0 u(t) + sen(ω0 t + θ)δ(t)
= cos(ω0 t + θ)ω0 u(t) + sen(θ)δ(t)
¨(t) = −sen(ω0 t + θ)ω 2 u(t) + cos(ω0 t + θ)ω0 δ(t) + δ(t)sen(θ)
f ˙
0
2 ˙
= −sen(ω0 t + θ)ω0 u(t) + cos(θ)ω0 δ(t) + δ(t)sen(θ)
Al´m disso sabemos que
e
L[f (t)] = s2 F (s) − sf (0− ) − f˙(0− ) = s2 F (s)
¨
e das duas express˜es acima tiramos o seguinte resultado
o
¨
L[f (t)] = s2 F (s)
2 ˙
= L[−sen(ω0 t + θ)ω0 u(t) + cos(θ)ω0 δ(t) + δ(t)sen(θ)]
s sen(θ) + ω0 cos(θ)
⇒ F (s) = 2
s2 + ω0
Problema 2.4 Refazer o exemplo 2.18 utilizando a rela¸˜o trigonom´trica sen(ωt+θ) =
ca e
sen(ωt)cos(θ) + cos(ωt)sen(θ)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-34-320.jpg)
![2.4. Transformada Inversa www.das.ufsc.br/labsil 35
2.4 Transformada Inversa
J´ foi mensionado anteriormente que a transformada de Laplace e sua respectiva fun¸˜o
a ca
no tempo est˜o relacionadas de forma biun´
a ıvoca, como ilustra a figura 2.10. A transfor-
mada inversa de Laplace nos permite encontrar a fun¸ao no tempo a partir do conheci-
c˜
mento da sua Transformada de Laplace .
Trans. Direta
f (t) F (s)
t≥0 Re[s] > c
Tranf. Inversa
Figura 2.10: Rela¸ao entre f (t) e sua transformada F (s)
c˜
Existem tabelas que s˜o bastante uteis na obten¸ao da tranformada inversa. No entanto
a ´ c˜
essas tabelas s˜o limitadas e no caso mais geral a maneira mais simples de se calcular
a
a transformada inversa ´ utilizar o m´todo de expans˜o por fra¸˜es parciais pois os
e e a co
fatores que resultam da expans˜o s˜o bem mais simples de serem convertidos ao dom´
a a ınio
do tempo. Este m´todo possui varia¸oes para p´los distintos, p´los m´ltiplos, p´los
e c˜ o o u o
complexos e vamos supor que a fun¸˜o a ser expandida por fra¸oes parciais ´ racional.
ca c˜ e
2.4.1 Fra¸oes parciais para p´los distintos
c˜ o
Seja F (s) uma transformada na forma fatorada, isto ´:
e
k(s + z1 )(s + z2 ) . . . (s + zm )
F (s) = , n>m
(s + p1 )(s + p2 ) . . . (s + pn )
onde −zi , (i = 1, 2, . . . , m), s˜o os zeros e −pi , (i = 1, 2, . . . , n) s˜o os p´los da fun¸ao
a a o c˜
F (s). A restri¸˜o n > m pode ser feita sem perda de generalidade como veremos num
ca
exemplo a seguir.
Quando todos os p´los s˜o distintos temos:
o a
a1 a2 an
F (s) = + + ··· + (2.5)
s + p1 s + p2 s + pn
onde ai s˜o constantes conhecidas como res´
a ıduos dos p´los pi , respectivamente, e s˜o
o a
calculados da seguinte forma:
ai = (s + pi )F (s)|s=−pi (2.6)
Isto pode ser facilmente verificado. Veja no caso do res´
ıduo do p´lo s = −p1 . Multipli-
o
cando (2.5) por s + p1 temos:
a2 an
(s + p1 )F (s) = a1 + (s + p1 ) + · · · + (s + p1 )
s + p2 s + pn](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-35-320.jpg)
![2.4. Transformada Inversa www.das.ufsc.br/labsil 36
Logo para s = −p1 encontramos (2.6) com i = 1. O procedimento ´ idˆntico para os
e e
demais p´los.
o
O interesse da expans˜o por fra¸˜es parciais ´ que cada termo da expans˜o (2.5) pode
a co e a
−pi t ai
ser facilmente transformado para o dom´ do tempo com a rela¸ao L[ai e u(t)] = s+pi ,
ınio c˜
logo:
a1 a2 an
f (t) = L−1 [F (s)] = L−1 + L−1 + · · · + L−1
s + p1 s + p2 s + pn
−p1 t −p2 t −pn t
= a1 e + a2 e + · · · + an e , t ≥ 0.
Note que a expans˜o por fra¸˜es parciais (2.5) ´ v´lida para p´los reais e complexos n˜o
a co e a o a
repetidos. Para p´los reais os res´
o ıduos (2.6) s˜o reais e para p´los complexos os res´
a o ıduos
s˜o complexos.
a
Exemplo 2.19 (P´los Reais) Calcule a fun¸˜o no tempo cuja transformada ´
o ca e
s+3
F (s) =
(s + 1)(s + 2)
Solu¸˜o: Com (2.5) e (2.6) se obt´m:
ca e
a1 a2
F (s) = +
s+1 s+2
a1 = F (s)(s + 1)|s=−1 = 2
a2 = F (s)(s + 2)|s=−2 = −1
Assim,
f (t) = L−1 [F (s)] = 2e−t − e−2t , t≥0
Exemplo 2.20 (N˜o Causal) Calcule a transformada inversa da fun¸˜o
a ca
s3 + 5s2 + 9s + 7
G(s) =
(s + 1)(s + 2)
Solu¸˜o: Como o grau do numerador ´ maior que o grau do denominador devemos
ca e
dividir um pelo outro at´ que o resto da divis˜o seja uma fun¸˜o com grau do numerador
e a ca
menor que o grau do denominador, como indicado a seguir.
s+3
G(s) = s + 2 +
(s + 1)(s + 2)
2 1
= s+2+ −
s+1 s+2](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-36-320.jpg)
![2.4. Transformada Inversa www.das.ufsc.br/labsil 37
Logo:
2 −1
g(t) = L−1 [G(s)] = L−1 [s] + L−1 [2] + L−1 + L−1
s+1 s+2
d
= δ(t) + 2δ(t) + 2e−t − e−2t , t ≥ 0−
dt
Exemplo 2.21 (P´los Complexos) Calcule a transformada inversa da fun¸˜o
o ca
2s + 12
F (s) =
s2 + 2s + 5
Solu¸˜o: Note que os p´los s˜o complexos pois s2 + 2s + 5 = (s + 1 + j2)(s + 1 − j2).
ca o a
Nesses casos a fun¸˜o temporal sempre envolve o produto de uma exponencial e um seno
ca
ou cosseno como indicado a seguir:
ω0
L[eαt senω0 t] = 2
(s − α)2 + ω0
s−α
L[eαt cosω0 t] = 2
(s − α)2 + ω0
Nas transformadas acima α ´ a parte real dos p´los e ω0 ´ a parte imagin´ria dos p´los.
e o e a o
Verifique que os p´los s˜o α ± jω0 . Para o exemplo em quest˜o temos s2 + 2s + 5 =
o a a
(s + 1)2 + 22 e com algumas manipula¸˜es alg´bricas obtem-se:
co e
2s + 12 ω0 s−α
F (s) = 2 + 22
=A 2 + ω2
+B 2
(s + 1) (s − α) 0 (s − α)2 + ω0
Logo 2s+12 = Aω0 +B(s−α). Como ω0 = 2 e α = −1 temos por igualdade polinomial
B = 2 e A = 5 o que resulta:
2 s+1
L−1 [F (s)] = 5L−1 2 + 22
+ 2L−1
(s + 1) (s + 1)2 + 22
= 5e−t sen2t + 2e−t cos2t, t ≥ 0.
Problema 2.5 Refa¸a o exemplo 2.21 utilizando o m´todo de expans˜o por fra¸˜es par-
c e a co
ciais indicado em (2.5). Obtenha a mesma express˜o para f (t).
a
2.4.2 Fra¸oes Parciais para p´los repetidos
c˜ o
Os m´todos da se¸ao anterior s˜o v´lidos para p´los distintos. Nesta se¸ao estudaremos
e c˜ a a o c˜
o caso de p´los repetidos baseado num exemplo que pode ser facilmente generalizado.
o](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-37-320.jpg)
![2.4. Transformada Inversa www.das.ufsc.br/labsil 38
Exemplo 2.22 Calcule a transformada inversa da fun¸˜o
ca
s2 + 2s + 3
F (s) =
(s + 1)3
Solu¸˜o: Como o p´lo tem multiplicidade trˆs a expans˜o por fra¸˜es parciais envolve
ca o e a co
trˆs termos:
e
b3 b2 b1
F (s) = + +
(s + 1)3 (s + 1)2 (s + 1)
onde os coeficientes bi , (i = 1, 2, 3), s˜o os res´duos a serem determinados.
a ı
Para determin´-los multiplique os dois lados por (s + 1)3 para obter:
a
(s + 1)3 F (s) = b3 + b2 (s + 1) + b1 (s + 1)2
Com a igualdade polinomial acima utilize um dos dois m´todos abaixo:
e
M´todo 1 Derivadas sucessivas de (s + 1)3 F (s)
e
⇒ b3 = (s + 1)3 F (s)|s=−1
d
[(s + 1)3 F (s)] = b2 + 2b1 (s + 1)
ds
d
⇒ b2 = [(s + 1)3 F (s)]s=−1
ds
d2
[(s + 1)3 F (s)] = 2b1
ds2
1 d2
⇒ [(s + 1)3 F (s)]s=−1
2! ds2
M´todo 2 Atribuindo-se valores para s na igualdade
e
s = 0 ⇒ 3 = b3 + b2 + b1
s = −1 ⇒ 2 = b3
s = 1 ⇒ 6 = b3 + 2b2 + 4b1
Os dois m´todos acima levam aos mesmos valores dos res´
e ıduos: b3 = 2, b2 = 0, b1 = 1
e portanto:
2 0 1
L−1 [F (s)] = L−1 3
+ L−1 2
+ L−1
(s + 1) (s + 1) s+1
2 −t −t
= t e +0+e , t ≥ 0.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-38-320.jpg)

![2.6. Resolu¸˜o de Equa¸oes Diferenciais
ca c˜ www.das.ufsc.br/labsil 40
Veremos a seguir que um sinal cuja transformada de Laplace ´ uma fun¸˜o racional
e ca
que possui todos os p´los no semi-plano esquerdo estrito, isto ´, p´los com parte real
o e o
estritamente negativa, ´ um sinal de energia limitada. Para esses sinais a integral acima
e
existe e ´ finita. Seja o seguinte sinal:
e
x(t) = α1 + α2 e−2t + α3 e−t + k1 e−t senω0 t + k2 e−t cosω0 t, t≥0
A transformada de x(t) ´:
e
α1 α2 α3 k1 ω0 k2 (s + 1)
X(s) = L[x(t)] = + + + 2 + ω2
+ 2
s s + 2 s + 1 (s + 1) 0 (s + 1)2 + ω0
Note que todos os p´los possuem parte real negativa, exceto o p´lo na origem. Assim, os
o o
p´los reais de X(s) tornam-se expoentes de fun¸oes exponenciais decrescentes no tempo.
o c˜
Os p´los complexos est˜o associados ` sinais que causam oscila¸oes amortecidas. O
o a a c˜
amortecimento dessas oscila¸oes ´ definido pela parte real dos p´los (Re[p´los] = −1 no
c˜ e o o
caso) e a frequˆncia de oscila¸ao ´ definida pela parte imagin´ria do p´lo (Im[p´lo] =
e c˜ e a o o
ω0 ). O efeito temporal dos p´los com parte real negativa diminui exponencialmente e
o
desaparece completamente em regime permanente, isto ´, quando t → ∞.
e
Um sinal x(t) cuja transformada seja anal´ıtica no semi-plano direito 1 mas tenha um
p´lo simples na origem vai ter um n´ DC igual ao res´
o ıvel ıduo desse p´lo (α1 no caso acima).
o
O valor do sinal x(t) acima em regime permanente (t → ∞) ´ constante e igual ` α. Note
e a
que nesse caso o sinal n˜o tem energia limitada pois a integral acima vai divergir dado
a
que o sinal n˜o converge para zero em regime.
a
Assim, um sinal qualquer x(t) vai ter um valor zero em regime (converge para zero
quando t → ∞) apenas quando todos os p´los da transformada possuem parte real
o
negativa. Se a transformada possui um p´lo na origem ( e os demais no semi-plano
o
esquerdo estrito) o sinal ser´ constante com um n´
a ıvel DC n˜o nulo em regime. Em
a
qualquer outra situa¸ao o sinal ´ divergente, isto ´, n˜o ter´ um valor de regime finito.
c˜ e e a a
A energia do sinal ser´ limitada apenas no primeiro caso, isto ´, quando o sinal converge
a e
para zero quando t → ∞.
2.6 Resolu¸˜o de Equa¸˜es Diferenciais
ca co
Atrav´s das leis da f´
e ısica podemos obter um modelo de comportamento para todos os
sistemas. Para sistemas dinˆmicos esse modelo ´ uma equa¸˜o diferencial. Este ´ o caso
a e ca e
por exemplo de motores, circuitos, turbinas e todos os outros dispositivos estudados na
engenharia. Saber como o sistema se comporta para dadas condi¸˜es iniciais e uma dada
co
excita¸˜o ´ equivalente a saber resolver a equa¸˜o diferencial.
ca e ca
A Transformada de Laplace pode ser utilizada para resolver equa¸˜es diferenciais
co
lineares invariantes no tempo. Para isso basta transformar por Laplace cada um dos
1
Lembre-se que uma fun¸ao ´ anal´
c˜ e ıtica numa dada regi˜o quando ela n˜o possui p´los nessa regi˜o
a a o a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-40-320.jpg)
![2.6. Resolu¸˜o de Equa¸oes Diferenciais
ca c˜ www.das.ufsc.br/labsil 41
termos da equa¸ao dif. obtendo assim a transformada da fun¸ao que resolve a equa¸˜o.
c˜ c˜ ca
Em seguinda, utiliza-se a transformada inversa para encontrar a solu¸˜o no dom´
ca ınio do
tempo.
Exemplo 2.25 Resolva a seguinte equa¸˜o diferencial x +2x+5x = g(t), onde x(0) = a,
ca ¨ ˙
x(0) = b s˜o constantes dadas e g(t)=0.
˙ a
Solu¸˜o: Note que
ca
L[x] = X(s)
L[x] = sX(s) − x(0)
˙
L[¨] = s2 X(s) − sx(0) − x(0)
x ˙
Tomando-se a transformada dos dois lados da equa¸˜o se obt´m:
ca e
[s2 X(s) − sx(0) − x(0)] + 2[sX(s) − x(o)] + 5X(s) = 0
˙
s+2 1
⇒ X(s) = x(0) + 2 x(o)
˙
s2
+ 2s + 5 s + 2s + 5
De forma similar ao exemplo 2.21 temos:
s+1 1 1
X(s) = x(0) + 2 x(0) + 2 x(o)
˙
s2 + 2s + 5 s + 2s + 5 s + 2s + 5
e consequentemente
x(t) = L−1 [X(s)] = [e−t cos(2t) + 0.5e−t sen(2t)]x(0) + 0.5e−t sen(2t)x(0)
˙
que ´ a solu¸ao da eq. diferencial.
e c˜
Exemplo 2.26 Um determinado sistema ´ regido pela seguinte equa¸˜o diferencial x +
e ca ¨
2x + 5x = g(t), onde as condi¸˜es iniciais s˜o nulas, isto ´, x(0) = 0, x(0) = 0. Encontre
˙ co a e ˙
a resposta desse sistema quando o mesmo ´ excitado por um degrau de amplitude 3, isto
e
´, g(t) = 3u(t).
e
Solu¸˜o: Note que
ca
3
L[3u(t)] =
s
L[x] = X(s)
L[x] = sX(s) − x(0) = sX(s)
˙
L[¨] = s2 X(s) − sx(0) − x(0) = s2 X(s)
x ˙
Logo:
3
s2 X(s) + 2sX(s) + 5X(s) =
s
3 3 3 s+2
X(s) = 2 + 2s + 5)
= − 2
s(s 5s 5 s + 2s + 5](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-41-320.jpg)
![2.7. Respostas de Estado Zero e Entrada Zero www.das.ufsc.br/labsil 42
Note que s2 + 2s + 5 = (s − σ)2 + ω 2 onde σ, ω s˜o as partes real e imagin´ria dos p´los
a a o
2
(ra´zes de s + 2s + 5). Para o caso em quest˜o temos σ = −1, ω = 2 e portanto:
ı a
3 3 1 3 s+1
X(s) = − −
5s 5 (s + 1)2 + 22 5 (s + 1)2 + 22
Logo:
3 3 1 3 s+1
L−1 [X(s)] = x(t) = L−1 − L−1 2 + 22
− L−1
5s 5 (s + 1) 5 (s + 1)2 + 22
3 3 3
= − e−t sen2t − e−t cos2t, t ≥ 0.
5 10 5
A figura 2.11 ilustra o diagrama de simula¸ao anal´gica da equa¸˜o diferencial x + 2x +
c˜ o ca ¨ ˙
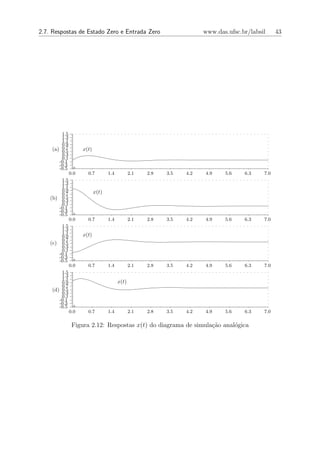
5x = g(t). A figura 2.12 mostra a resposta x(t) da equa¸ao para quatro situa¸˜es: (a)
c˜ co
g(t) = 0, x(0) = 1, x(0) = 0 ; (b) g(t) = 0, x(0) = 0, x(0) = 1 ; (c) g(t) = 3u(t), x(0) =
˙ ˙ ˙
0, x(0) = 0 ; (d) g(t) = 3u(t), x(0) = 1, x(0) = 1
˙
x(0)
˙ x(0)
g(t) + x
¨ x
˙ x
1 1
s s
- -
2
5
Figura 2.11: Diagrama de simula¸ao anal´gica
c˜ o
2.7 Respostas de Estado Zero e Entrada Zero
A resposta de todo sistema linear invariante no tempo pode ser decomposta em duas
parcelas: uma que depende do sistema e do sinal de entrada e outra que depende do
sistema e das condi¸˜es iniciais. A primeira parcela chamaremos de Resposta de Estado
co
Zero j´ que esta parcela indica como um sistema, inicialmente em repouso (condi¸oes
a c˜
iniciais nulas), responde a um dado sinal de entrada. A segunda parcela chamaremos de
Resposta de Entrada Zero pois ela indica como um sistema se comporta quando ´ deixado
e
para responder livremente `s suas condi¸oes inicias (sem excita¸ao externa). .
a c˜ c˜
As respostas de Estado Zero e Entrada Zero de um sistema descrito por (2.11) podem
ser determinadas atrav´s da Transformada de Laplace .
e
Exemplo 2.27 Encontre as respostas de Estado Zero e Entrada Zero do circuito RLC
s´rie da figura 2.14.
e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-42-320.jpg)
![2.7. Respostas de Estado Zero e Entrada Zero www.das.ufsc.br/labsil 44
Solu¸˜o: Do exemplo 2.28 temos que o comportamento dinˆmico entrada/sa´ do
ca a ıda
circuito ´ dado por (2.12). Tomando a transformada dos dois lados da equa¸˜o temos:
e ca
L[a2 y + a1 y + a0 y] = L[b0 x]
¨ ˙ (2.8)
Pela linearidade temos:
a2 L[¨] + a1 L[y] + a0 L[y] = b0 L[x]
y ˙
Sendo Y (s) = L[y] e X(s) = L[x], pela propriedade de deriva¸˜o no tempo:
ca
a2 [s2 Y (s) − sy(0) − y(0)] + a1 [sY (s) − y(0)] + a0 Y (s) = b0 X(s)
˙
⇒ (a2 s2 + a1 s + a0 )Y (s) = b0 X(s) + (a2 s + a1 )y(0) + a2 y(0)
˙
Portanto:
b0 a2 s + a1 a2
Y (s) = X(s) + y(0) + y(0)
˙
a2 s2 + a1 s + a0 a2 s2 + a1 s + a0 a2 s2 + a1 s + a0
Y (s) = F (s)X(s) + F0 (s)y(0) + F1 (s)y(0)
˙ (2.9)
onde
b0 a2 s + a1 a2
F (s) = , F0 (s) = , F1 (s) =
a2 s2 + a1 s + a0 a2 s 2+a s+a
1 0 a2 s 2+a s+a
1 0
Considerando f (t) = L−1 [F (s)], f0 (t) = L−1 [F0 (s)] e f1 (t) = L−1 [F1 (s)] podemos ent˜o
a
reescrever a express˜o acima com o aux´lio da anti-transformada na forma:
a ı
y(t) = L−1 [Y (s)] = L−1 [F (s)X(s)] + y(0)L−1 [F0 (s)] + y(0)L−1 [F1 (s)]
˙
= f (t) ∗ x(t) + y(0)f0 (t) + y(0)f1 (t)
˙ (2.10)
x(t)
F (s)
y(0) y(0)
˙
y(0) y(t)
F0 (s)
x(t) y(t)
F (s) y(0)
˙
F1 (s)
Figura 2.13: Respostas de Estado Zero e Entrada Zero
Note que f (t), f0 (t) e f1 (t) dependem apenas dos parˆmetros f´
a ısicos e da estrutura
entrada/sa´da do sistema. N˜o dependem nem da entrada x(t) nem da sa´ y(t) nem
ı a ıda
das condi¸˜es iniciais do sistema.
co
A respota de Estado Zero do circuito ´ a parcela de (2.10) que depende da entrada:
e
Yesz (s) = F (s)X(s) no dom´nio da frequˆncia ou de forma equivalente yesz (t) = f (t)∗x(t)
ı e
no dom´nio do tempo.
ı](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-44-320.jpg)


![2.8. Fun¸˜o de Transferˆncia e Estabilidade
ca e www.das.ufsc.br/labsil 47
Zero (2.14): Y (s)/X(s) = F (s). Assim, um sistema que possua a resposta de Estado
Zero (2.14) ter´ F (s) como fun¸ao de transferˆncia. Quando se conhece a fun¸˜o de
a c˜ e ca
transferˆncia F (s) de um sistema e a transformada do sinal de entrada X(s) se conhece
e
e e ´
tamb´m a resposta de Estado Zero do mesmo que ´ dada por (2.14). E importante
notar que a fun¸ao de transferˆncia depende apenas dos parˆmetros f´
c˜ e a ısicos do sistema e
da estrutura entrada/sa´ do mesmo. Veja o exemplo 2.27. A entrada e as condi¸oes
ıda c˜
inicias n˜o afetam a fun¸˜o de transferˆncia.
a ca e
Quando as condi¸oes iniciais s˜o nulas resposta total do sistema ´ a pr´pria resposta
c˜ a e o
de Estado Zero do mesmo, como pode ser visto nas equa¸oes (2.9) e (2.10).
c˜
Dom´
ınio do Tempo: y(t) = yesz (t) = f (t) ∗ x(t)
Dom´
ınio da Frequˆncia: Y (s) = Yesz (s) = F (s)X(s)
e
A fun¸˜o f (t) = L−1 [F (s)] recebe o nome de Resposta Impulsional pois f (t) ´ a re-
ca e
sposta do sistema quando as condi¸oes iniciais s˜o nulas e a entrada x(t) ´ um impulso
c˜ a e
no instante t = 0 (X(s) = 1).
Defini¸˜o 2.5 (Sistemas Causais ou N˜o-Antecipativos) Um sistema dinˆmico ´
ca a a e
dito ser Causal ou N˜o-Antecipativo se sua Resposta Impulsional ´ nula para t < 0.
a e
Pela defini¸ao acima nota-se que a resposta y(t) de um sistema causal excitado com um
c˜
sinal x(t), apresenta a seguinte propriedade: o valor de y(t)|t=tf s´ depende da entrada
o
x(t) e da resposta impulsional f (t) para valores de tempo t ≤ tf . Em outras palavras,
a dinˆmica de um sistema causal em qualquer instante de tempo t = tf depende (n˜o
a a
depende) da entrada e da resposta impulsional para valores de tempo menores (maiores)
que tf . Essa propriedade ´ mostrada a seguir.
e
∞
y(t) = f (t) ∗ x(t) = f (t − τ )x(τ )dτ
0
para t = tf temos f (tf − τ ) = 0 para τ > tf . Logo f (tf − τ )x(τ ) = 0 para τ > tf e
portanto:
tf
y(tf ) = f (tf − τ )x(τ )f τ
0
s´ depende de f (t) e x(t) para t < tf .
o
Outra no¸ao muito importante ´ a de estabilidade de sistemas.
c˜ e
Defini¸˜o 2.6 (Estabilidade de Sistemas) Um sistema ´ dito ser est´vel se todos os
ca e a
p´los da sua fun¸˜o de transferˆncia est˜o localizados no semi-plano esquerdo estrito,
o ca e a
isto ´, Re[p´los] < 0. Caso contr´rio o sistema ´ dito ser inst´vel.
e o a e a
Pela defini¸˜o acima nota-se que a estabilidade ´ uma propriedade intr´
ca e ınseca do sistema.
Ela s´ depende da sua fun¸˜o de transferˆncia e portanto dos seus parˆmetros f´
o ca e a ısicos e
da estrutura entrada/sa´
ıda.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-47-320.jpg)

![2.9. Diagrama de Blocos www.das.ufsc.br/labsil 49
R L
+ +
x(t) C y(t)
I(t)
- -
Sa´
ıda
Entrada SISTEMA
Figura 2.15: Diagrama entrada/sa´ de um circuito
ıda
Inicialmente vamos obter um diagrama onde apenas os sinais de entrada x(t) e sa´ ıda
y(t) s˜o de interesse, isto ´ a corrente n˜o aparece nas equa¸˜es. Obtendo as equa¸˜es
a e a co co
do circuito e eliminando a corrente ficamos com equa¸˜o diferencial em x(t) e y(t).
ca
˙
x(t) = RI(t) + LI(t) + y(t)
1 ⇒ RC y + LC y + y = x
˙ ¨
y(t) = C I(t)
˙
Sendo X(s) = L[x(t)] e Y (s) = L[y(t)] temos para condi¸˜es inciais nulas:
co
RCsY (s) + LCs2 Y (s) + Y (s) = X(s)
Logo:
1
Y (s) = X(s) (2.16)
LCs2 + RCs + 1
Portanto:
1
F (s) =
LCs2 + RCs + 1
X(s) Y(s)
F(s)
Figura 2.16: Diagrama de blocos simplificado
A fun¸˜o F (s) ´ a transferˆncia da tens˜o de entrada X(s) para a tens˜o de sa´ Y (s)
ca e e a a ıda
e para condi¸˜es iniciais nulas temos que a resposta do circuito para qualquer sinal de
co
entrada x(t) ´ dada por y(t) = x(t) ∗ f (t) onde f (t) = L−1 [F (s)] ´ a resposta impulsional
e e
do circuito.
Note que no diagrama de blocos acima foram eliminadas as informa¸˜es sobre todas as
co
outras vari´veis do circuito (corrente, etc). A Fun¸˜o de Transferˆncia d´ informa¸˜o
a ca e a ca
apenas sobre a rela¸˜o de causa-efeito entre as vari´veis de entrada e de sa´
ca a ıda.
´
E poss´vel, no entanto, explicitar a dependˆncia de outras vari´veis no diagrama de
ı e a
blocos atrav´s de simples manipula¸˜o de equa¸˜es. Por exemplo, para fazer aparecer a
e ca co
vari´vel corrente no diagrama de blocos do circuito temos:
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-49-320.jpg)





![Cap´
ıtulo 3
Resposta ao Degrau
3.1 Introdu¸˜o
ca
Um grande n´mero de problemas de controle consiste em se manter constante a vari´vel
u a
de sa´ıda. Veja por exemplo o problema de controle de posicionamento de uma antena
indicado na figura 1.4. A entrada do sistema, que representa o valor desejado da vari´vel
a
controlada (sa´ıda) ´ neste caso um degrau com amplitude igual ao valor desejado para
e
a sa´
ıda. Quando se quer mudar a posi¸˜o da antena de uma posi¸ao inicial, digamos
ca c˜
posi¸˜o zero, para uma nova posi¸˜o, digamos posi¸˜o um, o sinal de entrada deve ser
ca ca ca
um degrau unit´rio. Ao se aplicar um degrau na entrada desse sistema de controle, a
a
posi¸ao da antena vai evoluir da posi¸˜o zero para a posi¸˜o um segundo uma curva
c˜ ca ca
que depende de como o sistema de controle foi projetado. Curvas t´ ıpicas dessa evolu¸ao
c˜
podem ser encontradas na figura 3.1. Normalmente deseja-se um transit´rio r´pido, com
o a
poucas oscila¸oes e que a vari´vel controlada, posi¸˜o da antena no caso, v´ para o valor
c˜ a ca a
desejado sem erro significativo de posi¸ao em regime, isto ´, erro de regime despres´
c˜ e ıvel.
Para atender todos esses requisitos de performance, quando isso ´ poss´
e ıvel, o engenheiro
deve saber projetar adequadamente os filtros de controle do sistema. O primeiro passo,
no entanto, ´ saber especificar matematicamente os ´
e ındices de performance desejados
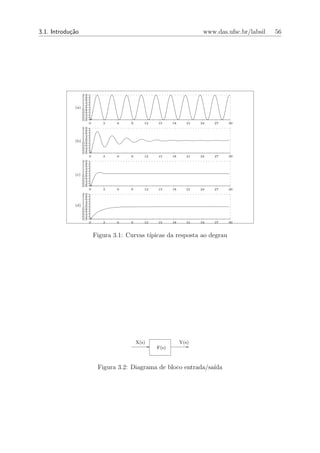
para a resposta. Veja na figura 3.1 que a resposta (a) ´ mais oscilat´ria que as demais. A
e o
resposta (c) atinge o valor de regime mais r´pido que as demais e todas as trˆs possuem
a e
erro de regime nulo (valor final da resposta ´ exatamente o valor desejado).
e
Neste cap´ıtulo estudaremos alguns ´
ındices de performance da resposta ao degrau que
nos permitir´ quantificar matematicamente o tamanho das oscila¸˜es da resposta, a rapi-
a co
dez da resposta e o erro de regime cometido.
Outros sinais de entrada como impulso e fun¸˜o rampa (x(t) = t) tamb´m s˜o de
ca e a
interesse. No entanto, para condi¸oes iniciais nulas, a resposta de um sistema (linear
c˜
invariante) ao impulso, degrau, e rampa est˜o ligadas entre si. Para ilustrar este fato,
a
seja F (s) a F.T. de um sistema linear invariante indicado na figura 3.2.
f (t) = L−1 [F (s)]
• Resposta Impulsional: X(s) = 1 ⇒ Y (s) = F (s) ⇒ y(t) = f (t)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-55-320.jpg)

![3.2. An´lise de Sistemas de Primeira Ordem
a www.das.ufsc.br/labsil 58
Exemplo 3.2 Podemos expressar a velocidade (ω) do eixo de um motor DC em fun¸˜o ca
da tens˜o de entrada (V ) atrav´s de uma equa¸˜o diferencial do tipo J ω + f ω = bV onde
a e ca ˙
b, J, f s˜o constantes f´sicas do motor. Mostre que esse sistema ´ de ordem 1.
a ı e
Solu¸˜o: Devemos mostrar que a fun¸˜o de transferˆncia possui apenas um p´lo.
ca ca e o
b
Tomando a transformada de Laplace encontramos ω = Js+f V que mostra o resultado
desejado.
1
A resposta ao degrau de um sistema cuja fun¸ao de transferˆncia ´ do tipo F (s) =
c˜ e e T s+1
´ obtida da seguinte forma:
e
1 1 1
Y (s) = X(s) =
Ts + 1 Ts + 1 s
com condi¸oes iniciais nulas e L[X(s)] = 1 .
c˜ s
Expandindo por fra¸˜es parciais e anti-transformando temos:
co
1 T
Y (s) = − ⇒ y(t) = 1 − e−t/T , t≥0
s Ts + 1
A resposta indicada acima possui propriedades interessantes:
x(t) entrada
y(t)
sa´
ıda
0 t
Figura 3.5: Resposta ao degrau de um sistema de primeira ordem padr˜o
a
dy 1
1) |
dt t=0
= T
2) Para t = T ⇒ y(T ) = 1 − e−1 = 0, 632, isto ´, decorridos T segundos a resposta
e
atinge 63, 2% do seu valor final de regime permanente.
t = 2T ⇒ y(2T ) = 1 − e−2 = 0, 865
t = 3T ⇒ y(3T ) = 1 − e−3 = 0, 950
t = 4T ⇒ y(4T ) = 1 − e−4 = 0, 982
t = 5T ⇒ y(5T ) = 1 − e−5 = 0, 993
As duas propriedades acima podem ser utilizadas para se encontrar o valor da constante
de tempo T quando a resposta ao degrau for obtida experimentalmente. Certifique-
se no experimento de que as condi¸oes iniciais s˜o realmente nulas e que a fun¸ao de
c˜ a c˜
1
transferˆncia ´ do tipo T s+1 .
e e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-58-320.jpg)


![3.3. An´lise de Sistemas de Segunda Ordem
a www.das.ufsc.br/labsil 61
A resposta ao degrau unit´rio ´ dada por Y (s) = F (s)R(s) com R(s) = 1/s. Logo:
a e
2
ωn
Y (s) =
(s2 + 2ξωn s + ωn )s
2
com o aux´ da tabela de anti-transformada temos:
ılio
eσt 1 − ξ2
y(t) = L−1 [Y (s)] = 1 − sen(ωd t + φ), φ = tan−1 (3.2)
1 − ξ2 ξ
Na figura 3.1(b) se encontra a resposta y(t) para ξ = 0, 1 e ωn = 2 e no caso 3.1(c) para
ξ = 0, 6 e ωn = 2.
Problema 3.1 Calcule o valor de regime permanente da resposta ao degrau de um sis-
tema na forma padr˜o (3.1). Qual ´ a diferen¸a entre os valores da entrada e da sa´
a e c ıda
em regime permanente ? Dica: Utilize o teorema do valor final.
3.3.3 Caso Superamortecido (ξ ≥ 1)
Se ξ ≥ 1 os p´los da fun¸˜o de transferˆncia (3.1) s˜o reais e os dois negativos. A sa´
o ca e a ıda
para uma entrada degrau unit´rio ´:
a e
2
ωn
Y (s) =
(s + s1 )(s + s2 )s
com s1,2 = (ξ ± ξ 2 − 1)ωn . Com o uso de tabelas de transformadas obtem-se:
e−s1 t e−s2 t ωn
y(t) = 1 + ( − )
s1 s2 2 ξ2 − 1
Esta resposta pode ser vista na figura 3.1(d) para ξ = 2 e ωn = 2. Para o caso particular
de ξ = 1 a express˜o y(t) acima precisa ser modificada e pode ser encontrada em [1].
a
Note que se ξ >> 1 ent˜o, para o mesmo valor de ωn , temos |s1 | >> |s2 | e portanto o
a
efeito do p´lo s1 sobre a resposta desaparece bem mais r´pido que o efeito do p´lo s2 que
o a o
est´ mais pr´ximo do eixo imagin´rio. Sendo assim para valores de ξ >> 1 o sistema
a o a
se torna extremamente lento. Um sistema de primeira ordem com um p´lo s2 teria uma
o
resposta muito parecida.
3.3.4 Caso inst´vel (ξ < 0)
a
Para valores negativos de ξ um dos p´los da fun¸˜o de transferˆncia (3.1) ´ positivo e
o ca e e
portanto a sa´ diverge exponencialmente (instabilidade).
ıda
Note que no caso do circuito do exemplo 3.3 a taxa de amortecimento ser´ sempre
a
positiva (ou nula quando R = 0) devido ` dissipa¸ao de energia no resistor.
a c˜
Problema 3.2 Mostre que quando ξ < 0 um dos p´los de F (s) em (3.1) ser´ sempre
o a
positivo e devido ` isso a resposta ao impulso cresce exponencialmente com uma taxa que
a
depende do p´lo positivo.
o](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-61-320.jpg)
![3.4. ´
Indices de desempenho www.das.ufsc.br/labsil 62
3.4 ´
Indices de desempenho
Nesta se¸ao estudaremos formas de classificar qu˜o boas s˜o as respostas da figura
c˜ a a
3.1. Como a resposta transit´ria ` um degrau normalmente apresenta oscila¸oes antes
o a c˜
de atingir o regime permanente, torna-se imperativo a cria¸ao de ´
c˜ ındices de desempenho
que permitam quantificar tamanho de oscila¸oes, tempo de dura¸ao do transit´rio, etc.
c˜ c˜ o
S˜o comuns os seguintes ´
a ındices:
2.0
1.8
1.6 Mp
faixa de erro toler´vel em regime
a
1.4
1.2
1.0
0.8
0.6
0.4
0.2
tp ts
0.0 +
0 3 6 9 12 15 18 21 24 27 30
Figura 3.7: ´
Indices de desempenho para resposta ao degrau
´
tp (instante de pico) E o tempo necess´rio para a resposta atingir o seu valor m´ximo.
a a
a ´
Mp (sobressinal m´ximo) E o valor relativo da diferen¸a entre o valor m´ximo da
c a
sa´ (ao longo do tempo) e o valor da sa´ em regime.
ıda ıda
y(tp ) − y(∞)
Mp =
y(∞)
ts (tempo de acomoda¸˜o) Tempo necess´rio para confinar a resposta numa faixa
ca a
em torno do seu valor de regime. Esta faixa caracteriza a tolerˆncia de erro, que
a
tipicamente vale 2 ou 5% do valor de regime).
A figura 3.7 ilustra os ´
ındices de desempenho descritos acima. Existem outros ´
ındices de
performance que n˜o foram indicados acima e podem ser encontrados em qualquer livro
a
de controle de sistemas, por exemplo [1].
Em geral n˜o ´ poss´ se determinar express˜es anal´
a e ıvel o ıcas para os ´
ındices de desem-
penho da resposta ao degrau indicados acima. No entanto, para sistemas de segunda](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-62-320.jpg)
![3.4. ´
Indices de desempenho www.das.ufsc.br/labsil 63
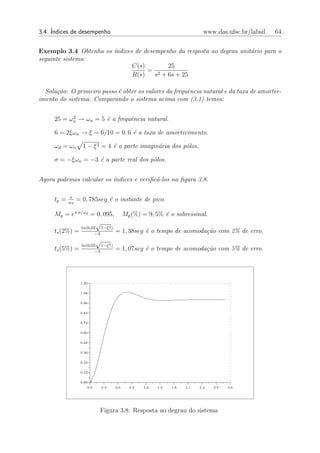
ordem do tipo (3.1) subamortecidos (1 > ξ > 0) isto ´ poss´ e essas express˜es s˜o
e ıvel o a
obtidas a seguir.
Instante de Pico (tp ): O instante de pico pode ser caracterizado como sendo
o primeiro instante de tempo (exceto a origem) para o qual a derivada temporal da
resposta ´ nula. Tomando a derivada temporal da resposta y(t) em (3.2) e igualando `
e a
zero encontramos:
π π
tp = = (3.3)
ωd ωn 1 − ξ 2
Sobressinal M´ximo (Mp ): Note que num sistema do tipo (3.1) o valor de regime da
a
resposta ao degrau unit´rio ´ um. Como y(∞) = 1 vamos utilizar (3.2) para obter:
a e
y(tp ) − y(∞) σ
π − √π ξ
Mp = = y(tp ) − 1 = e ωd = e 1−ξ2 (3.4)
y(∞)
Note que Mp depende somente de ξ e quando ξ ≥ 1 n˜o existe oscila¸ao e Mp n˜o tem
a c˜ a
mais sentido.
Tempo de Acomoda¸˜o (ts ): Diferentemente do Sobressinal e do intante de pico,
ca
n˜o existe uma express˜o anal´
a a ıtica exata para o tempo de acomoda¸ao ts . Existem ´bacos
c˜ a
que permitem a determina¸ao exata de ts . Veja por exemplo [1]. A seguir apresentamos
c˜
duas possibilidades para se obter uma aproxima¸ao de ts .
c˜
A resposta ao degrau do sistema (3.1) ´:
e
eσt 1 − ξ2
y(t) = 1 − sen(ωd t + φ) , φ = tan−1
1 − ξ2 ξ
Impondo que a amplitude do seno esteja dentro da faixa de tolerˆncia que caracteriza
a
o tempo de acomoda¸˜o temos uma condi¸˜o suficiente para garantir que o tempo de
ca ca
acomoda¸ao foi atingido com a dada tolerˆncia. Note que o valor de regime da resposta
c˜ a
´ y(∞) = 1 e a amplitude do seno tende ` zero quando t → ∞. Seja δ a tolerˆncia de
e a a
erro que define o tempo de acomoda¸ao. Impondo que a amplitude do seno esteja dentro
c˜
dessa tolerˆncia temos:
a
y(ts ) − y(∞) eσts ln(δ 1 − ξ2)
= sen(ωd + φ) ≤ δ ⇒ ts = (3.5)
y(∞) 1 − ξ2 σ
onde σ = −ξωn ´ a parte real dos p´los.
e o
Uma outra aproxima¸˜o muito comum para ts pode ser obtida por analogia com sis-
ca
temas de primeira ordem. Num sistema de primeira ordem o valor de regime da resposta
´ atingido ap´s 4 constantes de tempo com 2% de erro e ap´s 3 constantes de tempo com
e o o
5% de erro. Para um sistema de segunda ordem podemos aproximar ts definindo como
constante de tempo T = −1/σ e assim temos:
ts = 4T para 2% de erro ; ts = 3T para 5% de erro (3.6)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-63-320.jpg)







![3.6. Problemas complementares www.das.ufsc.br/labsil 74
a) Dois p´los em s = −1.
o
b) Sobressinal de 10% em 2 segundos.
c) Determine, considerando o caso (a) ou (b), o erro de regime permanente para um
degrau de amplitude 2.
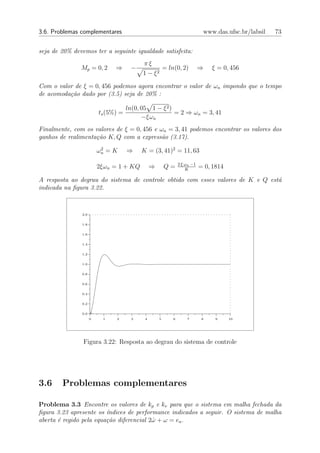
d) Calcule a resposta θ(t) do caso (a) para um degrau unit´rio.
a
r(t) ea (t) ω θ(t)
kp 10 sistema 1
s
- -
kv
kp
Figura 3.23: Sistema com realimenta¸˜o de velocidade e posi¸˜o
ca ca
Problema 3.4 Considere o sistema de controle de velocidade da figura 3.24. A resposta
ao degrau unit´rio desse sistema ´ indicada na figura 3.25. Encontre os valores de k1 e
a e
k2 sabendo que o motor ´ regido pela equa¸˜o diferencial ω + 10ω = Va .
e ca ˙
r Va ω θ
1
motor s
- -
k1 k2
Figura 3.24: Sistema de controle de velocidade
Problema 3.5 Um passo importante no estudo de sistemas de controle ´ a obten¸˜o de
e ca
modelos matem´ticos que descrevem o comportamento do sistema a ser controlado. No
a
caso de circuitos podemos utilizar a as leis de Kirchhhoff e as leis de Newton servem para
modelizar sistemas mecˆnicos. Existem sistemas que s˜o mais facilmente modelizados
a a
com a utiliza¸˜o da equa¸˜o de Lagrange, como ´ o caso de um microfone capacitivo.
ca ca e
Estude a modeliza¸˜o do microfone capacitivo apresentada em [6], p´ginas 59 ` 62, e
ca a a
verifique a utiliza¸˜o da equa¸˜o de Lagrange e a lineariza¸˜o ali apresentada para que o
ca ca ca
microfone possa ser modelizado como um sistema de segunda ordem do tipo (3.1).](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-74-320.jpg)



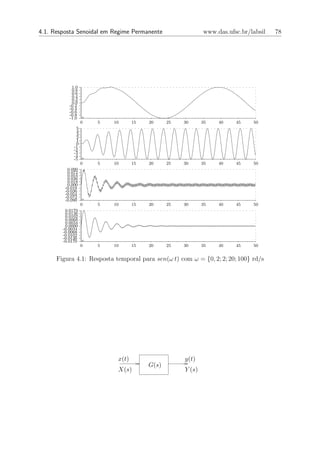
![4.1. Resposta Senoidal em Regime Permanente www.das.ufsc.br/labsil 79
Logo, para condi¸˜es iniciais nulas, a sa´ ´ dada por:
co ıda e
K(s + z1 ) . . . (s + zm ) A ω0
Y (s) = G(s)X(s) = 2
(s + s1 ) . . . (s + sn ) s2 + ω0
Se G(s) possui apenas p´los distintos, ent˜o a expans˜o por fra¸oes parciais de Y (s)
o a a c˜
conduz `:
a
a a
¯ b1 b2 bn
Y (s) = + + + + ··· +
s + jω0 s − jω0 s + s1 s + s2 s + sn
onde bi s˜o os res´
a ıduos dos p´los pi e a ´ o complexo conjugado de a. Antitransformando
o ¯e
a express˜o acima temos:
a
y(t) = a e−jω0 t + a ejω0 t + b1 e−s1 t + · · · + bn e−sn t ,
¯ t≥0
Para um sistema est´vel os p´los da F.T. G(s) possuem parte real negativa. Por-
a o
tanto ` medida que t → ∞ (Regime Permanente) os termos e−si t desapararecem pois
a
limt→∞ e−si t = 0.
Se G(s) possuir p´los m´ltiplos a resposta temporal acima ter´ termos do tipo tn e−sn t
o u a
que tamb´m desaparecem em regime permanente. Logo, independentemente do sistema
e
possuir p´los m´ltiplos ou n˜o, a resposta em regime estacion´rio de um sistema est´vel
o u a a a
para entrada x(t) = A sen(ω0 t) ´:
e
y(t) = a e−jω0 t + a ejω0 t
¯
onde os res´
ıduos a e a s˜o dados por:
¯ a
ω0 A A G(−jω0 )
a = G(s) s2 +ω2 (s + jω0 )|s=−jω0 = −2j
0
ω0 A A G(jω0 )
a = G(s) s2 +ω2 (s − jω0 )|s=jω0 =
¯ 2j
0
Sendo G(jω0 ) uma fun¸˜o complexa temos:
ca
G(jω0 ) = |G(jω0 )|ejφ(ω0 )
onde | · | indica m´dulo e φ(·) indica fase.
o
Im[G(jω0 )]
Fase → φ(ω0 ) = ∠G(jω0 ) = tan−1 { }
Re[G(jω0 )]
G(−jω0 ) = |G(−jω0 )|e−jφ(ω0 ) = |G(jω0 )|e−jφ(ω0 )
Exemplo 4.1 Mostre que uma fun¸˜o racional G(s) possui as seguintes propriedades
ca
para s = jω.
- A fase de G(jω), ∠G(jω), ´ uma fun¸˜o ´
e ca ımpar, isto ´, ∠G(−jω) = −∠G(jω)
e
- O m´dulo de G(jω), |G(jω)|, ´ uma fun¸˜o par, isto ´, |G(jω)| = |G(−jω)|.
o e ca e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-79-320.jpg)


![4.1. Resposta Senoidal em Regime Permanente www.das.ufsc.br/labsil 83
com B = A |G(jω0 )| , φ = ∠G(jω0 ) e G(jω0 ) = G(s) para s = jω0 .
2
ωn
G(jω0 ) = 2 2
−ω0 + ωn + j2ξω0 ωn
2
ωn 2ξω0 ωn
|G(jω0 )| = ; φ = −tan−1 [ 2 2
]
2
(ωn − 2
ω0 )2 + (2ξω0 ωn )2 ωn − ω0
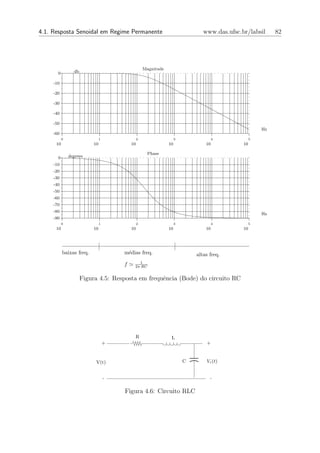
A figura 4.7 mostra as fun¸˜es |G(jω0 )| (em decibel) e ∠G(jω0 ) (em graus) para a faixa
co
de frequˆncia 10 ≤ w0 ≤ 105 (em Hertz) e trˆs valores distintos da resistˆncia: (a)
e 2
e e
R = 10Ω; (b) R = 100Ω; (c) R = 1KΩ.
Pela figura 4.7 podemos notar que no caso (a) o m´dulo (em decibel) aumenta numa
o
certa faixa de frequˆncia. Isto implica que as sen´ides de entrada nessa faixa de frequˆncia
e o e
s˜o amplificadas. Esse fenˆmeno de amplifica¸˜o da amplitude da sen´ide de entrada ´
a o ca o e
conhecido como ressonˆncia. Veremos adiante que essa amplifica¸˜o ocorre pr´ximo `
a ca o a
freq. natural n˜o amortecida ωn do sistema. A freq. onde a amplitude ´ m´xima (pico
a e a
do m´dulo) ´ conhecida como freq. de ressonˆncia. J´ no caso (c) n˜o existe pico
o e a a a
de ressonˆncia pois o m´dulo decai sempre indicando que as amplitudes da sen´ides de
a o o
sa´da s˜o sempre menores que as da entrada. Veremos tamb´m que o pico de ressonˆncia
ı a e a
depende do fator de amortecimento do sistema.
Magnitude
40 db
(a)
20
0
(b)
-20
(c)
-40
-60
Hz
-80
2 3 4 5
10 10 10 10
Phase
0 degrees
(a)
-20
-40 (b)
-60
-80
-100 (c)
-120
-140
-160
Hz
-180
2 3 4 5
10 10 10 10
Figura 4.7: Resposta em frequˆncia (Bode) do circuito RLC
e
Se compararmos as figuras 4.5 e 4.7 veremos que o m´dulo na altas frequˆncias decai
o e
(atenua¸˜o das amplitudes) segundo uma reta de inclina¸ao -20db/d´cada em 4.5 e -
ca c˜ e
40db/d´cada em 4.7. J´ a fase nas altas frequˆncias tende ` -90 graus em 4.5 e -180
e a e a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-83-320.jpg)
![4.3. Constru¸˜o do Diagrama de Bode
ca www.das.ufsc.br/labsil 84
graus em 4.7. Essas diferen¸as nas altas frequˆncias ocorrem devido ao fato do sistema
c e
da figura 4.5 ser de primeira ordem enquanto o sistema de 4.7 ´ de segunda ordem.
e
Nas baixas frequˆncias os dois circuitos possuem as mesmas caracter´
e ısticas, isto ´ o
e
m´dulo (em decibel) e a fase est˜o pr´ximos de zero. Isto indica que as sen´ides de sa´
o a o o ıda
e de entradas s˜o praticamente iguais pois tanto a defasagem quanto a atenua¸ao (ou
a c˜
amplifica¸˜o) s˜o muito pequenos nessa faixa de frequˆncia.
ca a e
4.2 Gr´ficos Logar´
a ıtmicos
Das figuras 4.5 e 4.7 podemos extrair informa¸oes importantes a respeito do com-
c˜
portamtento frequˆncial dos circuitos 4.4 e 4.6. Isso mostra a importˆncia que tem a
e a
representa¸˜o gr´fica da fun¸ao complexa G(jω) na an´lise frequencial de sistemas.
ca a c˜ a
Existem basicamente 3 tipos de gr´ficos que s˜o utilizados para se representar a fun¸˜o
a a ca
complexa G(jω). Cada tipo de gr´fico possui vantagens e aplica¸˜es espec´
a co ıficas.
O mais utilizado s˜o os diagramas de Bode. Estes gr´ficos se consagraram com os
a a
trabalhos de Bode sobre amplificadores realimentados na d´cada de 1940 e hoje s˜o
e a
muito utilizados na an´lise de sinais e sistemas de controle.
a
Nesses diagramas representa-se o m´dulo em decibel e a fase em graus, ambos em
o
fun¸˜o da frequˆncia (tipicamente em Hertz) numa escala logar´
ca e ıtmica. As figuras 4.5 e
4.7 s˜o os diagramas de Bode da resposta em frequˆncia dos circuitos 4.4 e 4.6. Lembre
a e
que o m´dulo em decibel de um n´mero complexo c = a + jb ´ dado por |c|db = 20 log(|c|)
o √ u e
onde |c| = a 2 + b2 ´ o m´dulo normal.
e o
Outro diagrama bastante utilizado em sistemas de controle ´ o diagrama de Nyquist.
e
Este diagrama ´ muito util na an´lise de estabilidade de sistemas realimentados. Aqui
e ´ a
a fun¸˜o G(jω) ´ representada em termos das suas coordenadas retangulares: a parte
ca e
real Re[G(jω)] e a parte imagin´ria Im[G(jω)]. Diferentemente dos diagramas de Bode,
a
o eixo das frequˆncias (tipicamente em radianos/segundo) n˜o aparece explicitamente
e a
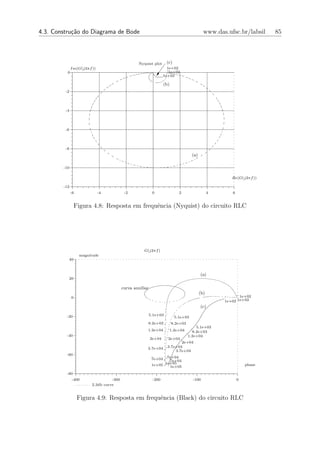
nos diagramas de Nyquist. A figura 4.8 mostra o diagrama de Nyquist da resposta em
frequˆncia do exemplo 4.3.
e
Outro diagrama `s vezes utilizado em projeto de sistemas de controle ´ o diagrama de
a e
Nichols (ou de Black como tamb´m ´ conhecido). Aqui representa-se o m´dulo (em deci-
e e o
bel) em fun¸˜o da fase (em graus). Como no diagrama de Nyquist, o eixo das frequˆncias
ca e
(tipicamente em radianos/segundo) n˜o aparece explicitamente. A figura 4.9 mostra o
a
diagrama de Black da resposta em frequˆncia do exemplo 4.3.
e
4.3 Constru¸˜o do Diagrama de Bode
ca
Como vimos anteriormente as fun¸oes G(jω) e G(−jω) s˜o complexas conjugadas, isto
c˜ a
´, possuem o mesmo m´dulo e fase com sinal trocado. Assim, se conhecemos o gr´fico
e o a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-84-320.jpg)
![4.3. Constru¸˜o do Diagrama de Bode
ca www.das.ufsc.br/labsil 86
de G(jω) podemos facilmente obter o gr´fico de G(−jω). Por esse motivo, de agora
a
em diante vamos sempre considerar G(jω) com ω ≥ 0. Isto implica que as sen´ides de
o
entrada s˜o do tipo sen(ωt) com ω ≥ 0. A resposta em frequˆncia para entradas do tipo
a e
sen(−ωt) ou ainda sen(ωt + θ) pode ser obtida da resposta em frequˆncia para sen(ωt)
e
com ω ≥ 0.
Nos diagramas de Bode o m´dulo ´ representado em dB e a fase em graus. Uma das
o e
propriedades fundamentais do m´dulo em dB ´ ilustrada no exemplo a seguir.
o e
Exemplo 4.4 Mostre que para dois n´meros complexos a e b quaisquer temos:
u
|ab|dB = |a|dB + |b|dB
∠ab = ∠a + ∠b
1
| | = −|a|dB
a
1
∠ = −∠a
a
Solu¸˜o: Sejam
ca
a = ax + jay = |a|ejφa
b = bx + jby = |b|ejφb
ay by
onde |a| = a2 + a2 , |b| =
x y b2 + b2 , φa = tan−1 [ ax ] e φb = tan−1 [ bx ]. Com isto vemos
x y
que |ab| = |a||b| e:
|ab|dB = 20log|ab|
= 20log|a| + 20log|b|
= |a|dB + |b|dB
Al´m disso:
e
∠ab = ej(φa +φb ) = ∠a + ∠b
1 1 1 1
| |= e | |dB = 20log| | = −20log|a| = −|a|dB
a |a| a a
1
∠ = e−jφa = −∠a
a
Assim, tanto o m´dulo quanto a fase do produto (ou divis˜o) de n´meros complexos
o a u
s˜o transformados em soma (ou subtra¸ao) dos m´dulos em dB e fases individuais de
a c˜ o
cada n´mero multiplicado (dividido). Isso facilita bastante a constru¸˜o manual dos
u ca
gr´ficos de m´dulo e fase. Outra vantagem ´ que a escala logar´
a o e ıtmica permite uma
melhor visualiza¸ao de fenˆmenos frequenciais d´
c˜ o ıspares (expans˜o da escala).
a
´
E comum nos diagramas de Bode se contar intervalos de frequˆncia por d´cada ou
e e
oitava.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-86-320.jpg)



![4.3. Constru¸˜o do Diagrama de Bode
ca www.das.ufsc.br/labsil 92
Magnitude
20 db
ξ = 0.1
10
0
ass´
ıntotas
-10
ξ=5
-20
-30
-40
Hz
-50
0.1 ωn ωn 10 ωn
Phase
0 degrees
-20
-40 ass´
ıntotas
-60
-80
ξ=5
-100
-120
-140
ξ = 0.1
-160
Hz
-180
0.1 ωn ωn 10 ωn
2
ωn
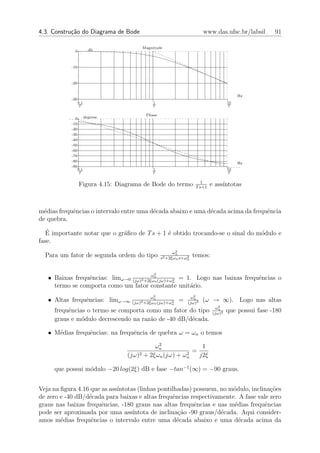
Figura 4.16: Diagrama de Bode do termo s2 +2ξωn s+ωn
2 e ass´
ıntotas
frequˆncia de quebra. A frequˆncia e o pico de ressonˆncia s˜o calculados da seguinte
e e a a
forma:
d d 1
|G(jω)| = 0 ⇒ [ ]=0
dω dω [1 − ( ω )2 ]2 + [2ξ ω ]2 ωn ωn
Resolvendo a express˜o acima encontramos
a
√
2
ωr = ωn 1− 2ξ 2 , 0≤ξ≤ (4.1)
2
√
Se ξ > 2/2 n˜o haver´ pico de ressonˆncia e o m´dulo decai monotonicamente de 1
a a a o
` zero.
a
√
Quando 0 ≤ ξ ≤ 2/2 o pico de ressonˆncia ´:
a e
1
Mr = |G(jω)|ω=ωr = (4.2)
2ξ 1 − ξ2
Problema 4.2 Considere o circuito RLC da figura 4.6 com R = 0 (oscilador ideal) e
suponha L = 0.01H, C = 1µF . Para esse sistema pede-se:
1. A fun¸˜o de transferˆncia G(s) do oscilador e seus p´los.
ca e o
2. Os diagramas de Bode da fun¸˜o G(jω).
ca
3. Explique porque n˜o se pode obter a resposta em frequˆncia desse sistema, isto ´,
a e e
porque nesse caso falham as rela¸˜es indicadas nas figuras 4.2 e 4.3.
co](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-92-320.jpg)



![4.5. Gr´ficos de Nyquist (ou polares)
a www.das.ufsc.br/labsil 97
Magnitude
0 db
-1
-2
-3
-4
-5
-6
-7
-8
-9 Hz
-10
-1 0 1 2 3
10 10 10 10 10
Phase
2 degrees
-2
-6
-10
-14
-18
-22
-26
Hz
-30
-1 0 1 2 3
10 10 10 10 10
Figura 4.22: Caso (b): Sistema de fase m´
ınima (r2 < r1 )
O grau relativo desse sistema ´ n − m. Note que n − m ≥ 0 para todo sistema de
e
interesse pr´tico.
a
Nas baixas frequˆncias temos:
e
lim G(jω) = K
ω→0
Logo o diagrama de m´dulo nas baixas frequˆncias ´ uma ass´
o e e ıntota de inclina¸ao zero
c˜
e valor dado por 20 log(K). O diagrama de fase nas baixas frequˆncias tamb´m ´ uma
e e e
ass´
ıntota de inclina¸˜o zero e valor zero pois K > 0. Nas altas frequˆncias temos:
ca e
am
lim G(jω) = lim K (jω)m−n
ω→∞ ω→∞ bn
O diagrama de m´dulo nas altas frequˆncias ´ uma ass´
o e e ıntota de inclina¸ao 20(m − n)
c˜
dB por d´cada e o valor onde esta ass´
e ıntota cruza o eixo das frequˆncias ´ dado por
e e
1
am n−m
ω = (K bn ) . O diagrama de fase nas altas frequˆncias tamb´m ´ uma ass´
e e e ıntota de
inclina¸˜o zero e valor 90(m − n) graus. Assim note que num sistema de fase m´
ca ınima
temos que se o m´dulo decai assintoticamente com 20(m − n) dB por d´cada a fase vale
o e
90(m − n) graus. Verifique este resultado no exemplo 4.7. Nesse exemplo n = m = 1
(grau relativo zero) e portanto no caso (b) quando r2 < r1 (sistema de fase m´ ınima) o
m´dulo tende ` uma ass´
o a ıntota de inclina¸˜o zero e a fase tende a zero graus nas altas
ca
frequˆncias. Isto n˜o ocorre no caso (a) quando r2 > r1 (sistema de fase n˜o m´
e a a ınima).
4.5 Gr´ficos de Nyquist (ou polares)
a
Como vimos na sub-se¸ao 4.2, podemos representar a fun¸ao complexa Gjω) em termos
c˜ c˜
das suas coordenadas polares. No eixo horizontal plotamos Re[G(jω)] e no eixo vertical](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-97-320.jpg)
![4.5. Gr´ficos de Nyquist (ou polares)
a www.das.ufsc.br/labsil 98
Im[G(jω)]. Este gr´fico recebe o nome de diagrama de Nyquist. A constru¸ao de um
a c˜
esbo¸o manual para esses gr´ficos n˜o ´ uma tarefa f´cil em geral. No entanto podemos
c a a e a
construir o diagrama de Nyquist a partir dos diagramas de Bode. Com alguns pontos
de m´dulo e fase dos diagramas de Bode podemos construir um esbo¸o do diagrama de
o c
Nyquist. O ponto (-1,0) do diagrama de Nyquist tem um papel muito importante na
an´lise de estabilidade de sistemas realimentados.
a
A figura 4.23 mostra os diagramas de Nyquist dos termos G1 (s) = (s + 1)−1 , G2 (s) =
(s+1)−2 , G3 (s) = (s+1)−3 , G4 (s) = (s+1)−4 . Note na figura 4.23 que o gr´fico de todos
a
Nyquist plot
Im(h(2i*pi*f))
0.1
0.24
0.19 ´
´
-0.0 0.001
´
´
0.15
´ 0.24
´ 0.001
´
´
0.011
´
-0.1
0.19
´ 0.021
0.011
´
´
0.032
´
-0.2 0.011
´
0.12
´
0.042
´
0.021
0.24
´ G1 ´
0.011
´
-0.3 0.15
´ 0.055
´
G2
´ 0.032
´
0.073
0.021
´
-0.4 0.19
´
0.093
´
0.093 ´ 0.24
´ 0.042
´
´ 0.12 0.19 0.12
´
0.021
-0.5
´ 0.15
´ ´
0.15
´ 0.032
´
G3 0.055
´
G4
-0.6 0.12
´ 0.073 ´
´ 0.042
0.093
´ 0.093
´ 0.032
´
0.073
´
-0.7 0.073
´
0.055
´
0.042
´ Re(h(2i*pi*f))
0.055
´
-0.8
-0.4 -0.2 -0.0 0.2 0.4 0.6 0.8 1.0
Figura 4.23: Diagrama de Nyquist de G1 (2πf ), G2 (2πf ), G3 (2πf ), G4 (2πf )
os termos come¸am no ponto (1,0) na frequˆncia zero e ` medida que a frequˆncia aumenta
c e a e
tendem para a origem. O termo de primeira ordem G1 (s) tende ` origem com fase -90
a
graus (tangente ao eixo imagin´rio negativo), como podemos verificar no diagrama de
a
Bode desse termo. O termo de segunda ordem G2 (s) tende ` origem com fase -180 graus
a
(tangente ao eixo real negativo), o de terceira ordem G3 (s) tende ` origem com fase -270
a
graus (tangente ao eixo imagin´rio positivo) e o de quarta ordem com fase -360 graus
a
(tangente ao eixo real positivo). Os n´meros indicados no diagrama s˜o os valores da
u a
frequˆncia em Hz para cada um dos casos. Um esbo¸o dos gr´ficos nesses casos simples
e c a
podem ser obtidos encontrando-se os valores onde as curvas cruzam os eixos. No caso
de G2 (s) por exemplo, basta calcular ω tal que Re[G2 (jω)] = 0 (no caso ω = 1 rad/s)
e com o valor da frequˆncia obtida calcular o valor de Im[G2 (jω)] nessa frequˆncia (no
e e
caso Im[G2 (j1)] = −0.5). Esse ´ o valor onde a curva de G2 (s) cruza o eixo imagin´rio.
e a
A presen¸a de integradores na fun¸˜o de transferˆncia de um sistema muda bastante a
c ca e
forma do diagrama de Nyquist. Veja na figura 4.24 como ficam os diagramas das fun¸oes c˜
1 1 1 1
H1 (s) = s(s+1) , H2 (s) = s(s+1)2 , H3 (s) = s(s+1)3 , H4 (s) = s(s+1)4 . Note que as fun¸oes
c˜
Hi (s), i = 1, 2, 3, 4 foram obtidas adicionando-se um integrador `s fun¸oes Gi (s) cujos
a c˜
diagramas est˜o na figura 4.23.
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-98-320.jpg)


![Cap´
ıtulo 5
Sinais e a Transformada de Fourier
Vimos nos m´todos de resposta em frequˆncia que para um sistema cuja fun¸˜o de
e e ca
transferˆncia ´ F (s), a fun¸ao F (jω) fornece informa¸oes importantes sobre o comporta-
e e c˜ c˜
mento do sistema em regime senoidal estacion´rio.a
Neste cap´ ıtulo estudaremos a transformada de Fourier e como essa transformada pode
nos auxiliar na an´lise de sinais e suas propriedades. A transformada de Fourier de um
a
sinal transforma um sinal f (t) numa fun¸ao complexa F (ω), conhecida como espectro do
c˜
sinal f (t). As equa¸oes que definem a transforma¸ao de vari´veis (f (t) para F (ω) e vice-
c˜ c˜ a
versa) s˜o dadas em (5.1). Estas opera¸oes, conhecidas como transformada de Fourier e
a c˜
sua inversa s˜o ilustradas na figura 5.1.
a
F[f (t)]
f (t) F (ω)
F −1 [F (ω)]
Figura 5.1: Operador Transformada de Fourier e seu inverso
1 ∞
f (t) = F −1 [F (ω)] = 2π −∞
F (ω)ejωt dω
(5.1)
∞ −jωt
F (ω) = F[f (t)] = −∞
f (t)e dt
Existem sinais f (t) para os quais n˜o ´ poss´ se calcular a Transformada de Fourier.
a e ıvel
Uma condi¸˜o suficiente para a existˆncia da Transformada de Fourier ´ indicada a
ca e e
seguir:
∞ ∞ ∞
|F (ω)| = | f (t)e−jωt dt| ≤ |f (t)e−jωt | dt = |f (t)| dt < ∞
−∞ −∞ −∞
Logo, se o sinal f (t) ´ integr´vel em m´dulo a sua transformada vai seguramente existir.
e a o
No entanto o contr´rio n˜o ´ verdade em geral, pois sinais como seno, cosseno, e degrau
a a e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-101-320.jpg)

![5.2. Energia de sinais www.das.ufsc.br/labsil 103
Por exemplo, se f (t) representa a tens˜o ou corrente num resistor unit´rio, a energia do
a a
sinal f (t) ´ dada pela integral acima. Os sinais que possuem energia limitada (E < ∞)
e
s˜o portanto de grande interesse pr´tico.
a a
Veremos a seguir que a energia de um sinal est´ ligada ao m´dulo da Transformada de
a o
Fourier do sinal em quest˜o. Antes por´m, devemos relembrar algumas propriedades da
a e
fun¸˜o F (ω) dadas no exemplo 5.1.
ca
Exemplo 5.1 Mostre que |F (ω)| ´ uma fun¸˜o par de ω e ∠F (ω) ´ uma fun¸˜o ´
e ca e ca ımpar
de ω.
Solu¸˜o: Seja F (ω) = M (ω)ejφ(ω) onde M (ω) e φ(ω) denotam respectivamente o
ca
m´dulo e a fase de F (ω). Note que f (t) ´ um sinal real logo f (t) e seu conjugado
o e
complexo f (t) s˜o iguais, isto ´ f (t) = f (t). Ent˜o a conjuga¸˜o complexa de F (ω)
a e a ca
resulta:
∞ ∞ ∞
F (ω) = f (t)e−jωt dt = f (t)e−jωt dt = f (t)ejωt dt = F (−ω)
−∞ −∞ −∞
Portanto F (−ω) = F (ω) = M (ω)e−jφ(ω) que nos leva `s conclus˜es desejadas:
a o
|F (ω)| = |F (−ω)| = M (ω) (fun¸˜o par)
ca
∠F (ω) = −∠F (−ω) (fun¸˜o ´
ca ımpar)
Podemos agora mostrar que a energia de um sinal est´ ligada ao m´dulo da Transfor-
a o
mada de Fourier do sinal em quest˜o. Com f (t) de (5.1) obtemos:
a
∞ ∞ ∞ ∞
2 1
E = f (t) dt = f (t) f (t) dt = f (t) F (ω)ejωt dω dt
−∞ −∞ −∞ 2π −∞
∞ ∞ ∞
1 −jωt 1
= F (ω) f (t)e dt dω = F (ω)F (ω)dω
2π −∞ −∞ 2π −∞
Como F (ω)F (ω) = |F (ω)|2 ficamos com:
∞
1
E= |F (ω)|2 dω (5.3)
2π −∞
A f´rmula acima ´ conhecida como teorema de Parseval. Note ainda que como |F (ω)| ´
o e e
uma fun¸ao par temos:
c˜
1 ∞
E= |F (ω)|2 dω (5.4)
π 0
|F (ω)|2
A quantidade π
´ `s vezes chamada de densidade espectral de energia.
ea
Exemplo 5.2 Encontre o intervalo de frequˆncia [−ω0 , ω0 ] que cont´m metade da energia
e e
−t
do sinal f (t) = e , t ≥ 0.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-103-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 104
Solu¸˜o: Seja ET a energia total do sinal dada por
ca
∞ ∞
1
ET = f (t)2 dt = e−2t dt =
−∞ 0 2
1
Como F (ω) = F[f (t)] = 1+jω
temos que a energia no intervalo [−ω0 , ω0 ] ´ dada por:
e
ω0 ω0
1 1 1 1
Eω0 = |F (ω)|2 dω = 2
dω = tan−1 (ω0 )
2π −ω0 π 0 1+ω π
Queremos metade da energia total, ou seja, 1/4, logo:
1 1
tan−1 (ω0 ) = ⇒ ω0 = 1rad/s
π 4
Logo metade da energia do sinal est´ no intervalo de frequˆncia entre [−1, 1].
a e
5.3 C´lculo de algumas transformadas
a
5.3.1 Sinal Exponencial Unilateral (t ≥ 0)
Seja:
f (t) = e−at u(t), a>0
Ent˜o:
a
∞ ∞
−at −jωt 1
F (ω) = F[f (t)] = e u(t)e dt = e−(a+jω)t dt =
−∞ 0 a + jω
Note que F (ω) = F (s)|s=jω pois a regi˜o de convergˆncia da Transformada de Laplace
a e
F (s) cont´m o eixo imagin´rio jω. Se a < 0 a Transformada de Fourier n˜o mais existe.
e a a
5.3.2 Sinal Porta
Usaremos a nota¸ao Gτ (t) para definir o sinal porta (gate) de largura τ como indicado
c˜
a seguir.
1, |t| < τ /2
Gτ (t) =
0, |t| > τ /2
A transformada do sinal porta ´ calculada da seguinte forma.
e
τ /2
1 jωτ /2
F (ω) = F[Gτ (t)] = e−jωt dt =
(e − e−jωτ /2 )
−τ /2 jω
sen(ωτ /2) ωτ
= τ = τ Sa [ ]
(ωτ /2) 2](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-104-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 106
sen(x)
A fun¸˜o Sa(x) =
ca x
´ conhecida como fun¸ao amostragem (sampling) e est´ indicada
e c˜ a
na figura 5.3.
ωτ
Gτ (t) ←→ τ Sa ( ) (5.5)
2
Note que F (ω) nesse caso ´ real pois f (t) ´ par. Se f (t) for ´
e e ımpar ent˜o F (ω) ´ imagin´rio
a e a
puro.
5.3.3 Sinal Impulso:
A nota¸˜o para a fun¸˜o impulso unit´rio que ocorre no instante zero ´ δ(t). Como
ca ca a e
δ(t) = 0 para t = 0 temos:
∞ ∞ ∞
δ(t)f (t)dt = δ(t)f (0)dt = f (0) δ(t) dt = f (0)
−∞ −∞ −∞
Logo:
∞
F (ω) = F[δ(t)] = δ(t)e−jωt dt = ej0 = 1
−∞
δ(t) ←→ 1
O seguinte resultado ser´ util na prova de alguns teoremas.
a´
Seja f (t) a fun¸˜o definida a seguir.
ca
K
f (t) = Sa (Kt)
π
Podemos mostrar que a ´rea dessa fun¸˜o ´ unit´ria para qualquer valor do parˆmetro
a ca e a a
K, isto ´,
e
∞
K
Sa (Kt) dt = 1, ∀K
−∞ π
Com esse resultado podemos ainda mostrar que quando K tende ` infinito a fun¸ao f (t)
a c˜
tende ` fun¸ao impulso.
a c˜
K
δ(t) = lim Sa (Kt) (5.6)
K→∞ π
5.3.4 Fun¸oes Constante, Sinal e Degrau
c˜
A transformada do degrau n˜o pode ser facilmente obtida pela aplica¸˜o da defini¸ao.
a ca c˜
A seguir veremos como obtˆ-la com o aux´ das transformadas das fun¸oes sinal e
e ılio c˜
constante.
A fun¸˜o constante unit´ria pode ser vista como o caso limite da fun¸ao porta, isto ´
ca a c˜ e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-106-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 107
limτ →∞ Gτ (t) = 1. Logo com (5.5),(5.6) temos que
F[1] = F[ lim Gτ (t)] = lim F[Gτ (t)]
τ →∞ τ →∞
= lim τ Sa (ωτ /2)
τ →∞
τ
= 2π lim Sa (ωτ /2)
τ →∞ 2π
= 2πδ(ω) (5.7)
A fun¸ao sinal ´ definida como sendo:
c˜ e
1, t>0
sgn(t) =
−1, t < 0
sgn(t)
1
0 t
-1
Figura 5.4: Fun¸˜o Sinal
ca
A fun¸ao sinal pode ser expressa atrav´s do seguinte limite:
c˜ e
sgn(t) = lim (e−at u(t) − eat u(−t))
a→0
e portanto podemos calcular sua transformada da seguinte forma:
F[sgn(t)] = F[ lim (e−at u(t) − eat u(−t))]
a→0
= lim F[e−at u(t) − eat u(−t)]
a→0
−2jω 2
= lim 2 + ω2
= (5.8)
a→0 a jω
O resultado acima nos permite calcular agora a Transformada do degrau. Como u(t) =
1
2
(1 + sgn(t)) temos:
1 1 1
F[u(t)] = F[1] + F[sgn(t)] = πδ(ω) +
2 2 jω
Resumindo:
1 ←→ 2πδ(ω)
2
sgn(t) ←→ (5.9)
jω
1
u(t) ←→ πδ(ω) +
jω](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-107-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 108
5.3.5 Sinais Senoidais
Nos ocuparemos agora das transformadas das fun¸oes senoidais. Pela defini¸ao temos
c˜ c˜
∞ T /2
F[cos(ω0 t)] = cos(ω0 t)e−jωt dt = lim cos(ω0 t)e−jωt dt
−∞ T →∞ −T /2
ejω0 t +e−jω0 t
como cos(ω0 t) = 2
temos:
T (ω − ω0 ) (ω + ω0 )
F[cos(ω0 t)] = lim {Sa [T ] + Sa [T ]}
T →∞ 2 2 2
com (5.6) temos:
F[cos(ω0 t)] = π[δ(ω − ω0 ) + δ(ω + ω0 )] (5.10)
Da mesma forma obtem-se:
F[sen(ω0 t)] = jπ[δ(ω + ω0 ) − δ(ω − ω0 )] (5.11)
Note que a Transformada de Fourier do sen(ω0 t) e cos(ω0 t) s´ n˜o ´ nula nas frequˆncias
o a e e
±ω0 . Isto mostra que esses sinais possuem energia concentrada nessas frequˆncias. Isso
e
n˜o ocorreria se as fun¸˜es fossem sen(ω0 t)u(t) ou cos(ω0 t)u(t). Nesse caso obter´
a co ıamos:
π jω
F[cos(ω0 t)u(t)] = [δ(ω − ω0 ) + δ(ω + ω0 )] + 2
2 ω0 − ω 2
π ω0
F[sen(ω0 t)u(t)] = [δ(ω − ω0 ) − δ(ω + ω0 )] + 2
2j ω0 − ω 2
que ´ algo bastante similar ao que obter´
e ıamos a partir da Transformada de Laplace para
s = jω.
s jω
F (s) = L[cos(ω0 t)] = 2 2
→ F (jω) = 2
ω0 + s ω0 − ω 2
ω0 ω0
F (s) = L[sen(ω0 t)] = 2 2
→ F (jω) = 2
ω0 +s ω0 − ω 2
Os resultados n˜o coincidem pois a regi˜o de convergˆncia da Transformada de Laplace
a a e
dessas duas fun¸˜es n˜o cont´m o eixo imagin´rio.
co a e a
5.3.6 Exponencial Eterna ejω0 t
Como ejω0 t = cos(ω0 t) + jsen(ω0 t) temos com os resultados anteriores:
F[ejω0 t ] = 2πδ(ω − ω0 ) (5.12)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-108-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 109
5.3.7 Fun¸oes Peri´dicas
c˜ o
A transformada de fun¸oes peri´dicas se faz com o aux´ da decomposi¸ao dessas
c˜ o ılio c˜
fun¸˜es via s´rie exponencial de Fourier.
co e
Seja f (t) uma fun¸ao peri´dica de per´
c˜ o ıodo T . Ent˜o f (t) pode ser expressa em termos
a
da S´rie exponencial de de Fourier indicada abaixo.
e
∞
f (t) = Fn ejωn t , t0 < t < t0 + T (5.13)
n=−∞
onde ω0 = 2π ´ conhecido como frequˆncia fundamental do sinal e ωn = nω0 , n =
T
e e
1, 2, 3, ... s˜o as frequˆncias harmˆnicas do sinal. A primeira harmˆnica ´ a pr´pria
a e o o e o
frequˆncia fundamental. O coeficiente F0 ´ o valor m´dio do sinal no per´
e e e ıodo e Fn , n =
±1, ±2, ±3, ... s˜o os coeficientes harmˆnicos.
a o
t0 +T
1
F0 = f (t)dt (5.14)
T t0
t0 +T
1
Fn = f (t)e−jωn t dt (5.15)
T t0
Tomando-se as transformadas dos dois lados de (5.13) temos:
∞ ∞
F[f (t)] = Fn F[ejnω0 t ] = 2π Fn δ(ω − nω0 ) (5.16)
n=−∞ n=−∞
A express˜o acima mostra que a transformada de Fourier de um sinal peri´dico n˜o ´
a o a e
nula apenas nas frequˆncias harmˆnicas do sinal. Logo a energia de sinais peri´dicos est´
e o o a
concentrada nas frequˆncias harmˆnicas do sinal.
e o
Problema 5.1 Pela defini¸˜o acima mostre que Fn ´ F−n s˜o complexos conjugados.
ca e a
Sugest˜o: use a f´rmula de Euler ejx = cos(x) + jsen(x).
a o
Problema 5.2 Mostre que se f (t) ´ uma fun¸˜o par, isto ´ f (t) = f (−t), ent˜o Fn
e ca e a
e F[f (t)] s˜o ambos reais e se f (t) ´ ´
a e ımpar, isto ´ f (t) = −f (−t), Fn e F[f (t)] s˜o
e a
jx
puramente imagin´rios. Sugest˜o: use a f´rmula de Euler e = cos(x) + jsen(x).
a a o
Exemplo 5.3 Calcule a transformada de Fourier da fun¸˜o peri´dica da figura 5.5.
ca o
Solu¸˜o: Podemos verificar pela figura que o valor m´dio de f (t) no per´
ca e ıodo ´ nulo,
e
2π
isto ´ F0 = 0. A frequˆncia fundamental do sinal ´ ω0 = T = 1. Como f (t) ´ ´
e e e e ımpar](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-109-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 110
f (t)
1
π 2π
0 t
-1
T
Figura 5.5: Fun¸˜o onda quadrada de per´
ca ıodo 2π.
temos:
1 t0 +T 1 2π
Fn = f (t) e−jωn t dt = f (t) (cos(ωn t) − jsen(ωn t))dt
T t0 2π 0
−j 2π −j π 2π
= f (t)sen(ωn t)dt = [ sen(nω0 t)dt + −sen(nω0 t) dt]
2π 0 2π 0 π
−j −cos(nω0 t) π cos(nω0 t) 2π
= ([ ]0 + |π )
2π nω0 nω0
−j
= (−cos(nπ) + 1 + cos(n2π) − cos(nπ))
2nπ
−j −2j
= (2 − 2cos(nπ)) = se n ´ ´
e ımpar e 0 se n ´ par e
2nπ nπ
Logo para n ´mpar temos:
ı
∞
−2j
F[f (t)] = 2π δ(ω − n)
n=−∞
nπ
Al´m disso, com (5.13) e n ´
e ımpar ficamos com:
∞ ∞
−2j jnt −2j
f (t) = e = (cos(nt) + jsen(nt))
n=−∞
nπ n=−∞
nπ
∞
4 1
= sen(nt)
π n=1
n
Exemplo 5.4 Calcule a Transformada de Fourier da fun¸˜o trem de impulsos indicada
ca
na figura 5.7.
Solu¸˜o: A fun¸˜o trem de impulsos ´ uma fun¸˜o peri´dica e se denotarmos seu
ca ca e ca o
per´odo por T podemos escrevˆ-la da seguinte forma:
ı e
∞
δT (t) = δ(t − nT )
n=−∞](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-110-320.jpg)
![5.3. C´lculo de algumas transformadas
a www.das.ufsc.br/labsil 111
f (t)
1.5
n=1
n=3
1.1 n=5
n=∞
0.7
0.3
-0.1
-0.5
-0.9
-1.3
t
0 1 2 3 4 5 6 7
Figura 5.6: Aproxima¸ao de sinais pela s´rie trigonom´trica de Fourier.
c˜ e e
Como δT (t) ´ peri´dica de per´odo T temos:
e o ı
∞
F[δT (t)] = 2π Fn δ(ω − nω0 )
n=−∞
onde Fn , n = ±1, ±2, ±3, ... s˜o os coeficiente harmˆnicos do sinal que s˜o dados por:
a o a
T /2 T /2
1 1 1 −jnω0 0 1
Fn = δT (t)e−jnω0 t dt = δ(t)ejnω0 t dt = e =
T −T /2 T −T /2 T T
Logo
∞
2π
F[δT (t)] = δ(ω − nω0 ) = ω0 δω0 (ω)
T n=−∞
δT (t) F[δT (t)]
δ(t − nT ) ω0 δ(ω − nω0 )
... ... ... ...
t ω
T ω0
Figura 5.7: Trem de impulsos e sua transformada
δT (t) ←→ ω0 δω0 (ω)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-111-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 112
5.4 Propriedades da transformada
Em primeiro lugar, vale a pena salientar que para fun¸oes integr´veis em m´dulo pode-
c˜ a o
mos obter a transformada de Fourier diretamente da transformada de Laplace com a
mudan¸a de vari´vel s = jω. Portanto, para fun¸oes integr´veis em m´dulo todas as pro-
c a c˜ a o
priedades da transformada de Laplace continuam v´lidas para a transformada de Fourier.
a
A seguir apresentaremos algumas das propriedades mais importantes.
5.4.1 Linearidade
Se F[f1 (t)] = F1 (ω) e F[f2 (t)] = F2 (ω) ent˜o:
a
F[α1 f1 + α2 f2 ] = α1 F1 (ω) + α2 F2 (ω)
5.4.2 Simetria
Se F[f (t)] = F (ω) ent˜o F[F (t)] = 2π f (−ω).
a
Veja como aplicar essa propriedade para descobrir a transformada de Fourier da fun¸ao
c˜
sampling. Sabemos de (5.5) que F[Gτ (t)] = τ Sa( ωτ ). Por compara¸˜o com a nota¸ao
2
ca c˜
ωτ
acima temos f (t) = Gτ (t) e F (ω) = τ Sa( 2 ). Logo, pela propriedade de simetria
F[F (t)] = 2π f (−ω) deduzimos
tτ
F[τ Sa( )] = 2π Gτ (−ω)
2
Com a mudan¸a de vari´vel τ = Ω e lembrando que Gτ (−ω) = Gτ (ω) pois a fun¸ao porta
c a 2
c˜
´ par ficamos com o resultado desejado:
e
π
F[Sa(Ωt)] = G2Ω (ω) (5.17)
Ω
5.4.3 Escalonamento
Se F[f (t)] = F (ω) ent˜o:
a
1 ω
F[f (at)] = F( )
|a| a
Exemplo 5.5 Calcule F[G2γ (t)].
Solu¸˜o: Como j´ sabemos que F[Gτ (t)] = τ Sa ( ωτ ) com a mudan¸a de vari´vel τ = 2γ
ca a 2
c a
temos que F[G2γ (t)] = 2γ Sa (ωγ). Esta mudan¸a de vari´vel corresponde ` aplica¸˜o da
c a a ca
propriedade de escalonamento acima com o fator de escala a = 0.5, isto ´ com a mudan¸a
e c
de escala t = 0.5 t .](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-112-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 113
5.4.4 Deslocamento em Frequˆncia e Modula¸˜o
e ca
Se F[f (t)] = F (ω) ent˜o:
a
F[f (t)ejω0 t ] = F (ω − ω0 )
Note que multiplicar f (t) pela exponencial complexa ejω0 t corresponde a deslocar todo
o espectro de f (t) centrando-o na frequˆncia ω0 .
e
Na pr´tica ao inv´s de utilizar exponenciais complexas para deslocar o espectro do
a e
sinal utiliza-se fun¸˜es do tipo cos(ω0 t). Veja oque acontece com o espectro do sinal ap´s
co o
a multiplica¸ao de f (t) pelo cosseno.
c˜
ejω0 t + e−jω0 t
F[f (t) cos(ω0 t)] = F[f (t) ( )]
2
F[f (t) ejω0 t ] + F[f (t) e−jω0 t ]
=
2
F (ω + ω0 ) + F (ω − ω0 )
=
2
Ao multiplicar um sinal f (t) pelo cos(ω0 t) estamos atenuando pela metade e deslocando
todo o espectro do sinal f (t) para as frequˆncias ±ω0 . Este artif´ ´ conhecido como
e ıcio e
modula¸ao em amplitude pois o sinal f (t), conhecido como sinal modulado, ´ a amplitude
c˜ e
do cosseno. A fun¸ao cos(ω0 t) recebe o nome de portadora de frequˆncia ω0 . A figura
c˜ e
5.8 mostra a transformada de Fourier do sinal porta de largura unit´ria G1 (t). A figura
a
5.9 ilustra a o espectro do sinal modulado cos(100t)G1 (t).
F[G1 (t)]
1.1
0.9
0.7
0.5
0.3
0.1
-0.1
-0.3 ω
-100 -80 -60 -40 -20 0 20 40 60 80 100
Figura 5.8: Transformada de Fourier do sinal porta de largura unit´ria G1 (t).
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-113-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 114
F[cos(100t)G1 (t)]
0.5
0.4
0.3
0.2
0.1
0
-0.1 ω
-200 -160 -120 -80 -40 0 40 80 120 160 200
Figura 5.9: Transformada de Fourier do sinal cos(100t)G1 (t).
A modula¸˜o de sinais ´ utilizada em comunica¸oes de r´dio transmiss˜o AM. Em
ca e c˜ a a
controle de sistemas, a modula¸˜o ´ utilizada para deslocar a energia do sinal de controle
ca e
para a faixa de frequˆncia onde o sistema funciona.
e
A recupera¸˜o de um sinal modulado (demodula¸˜o) pode ser feita de v´rias formas.
ca ca a
Uma delas consiste em modular novamente o sinal e em seguida filtrar as frequˆncias
e
indesejadas.
cos(ω0 t) cos(ω0 t)
f(t) f (t)cos(ω0 t) f (t)cos2 (ω0 t) FILTRO f(t)
MOD MOD IDEAL
Figura 5.10: Demodula¸˜o de um sinal
ca
5.4.5 Deslocamento no Tempo
Se F[f (t)] = F (ω) ent˜o:
a
F[f (t − t0 )] = F (ω)e−jωt0
Note que deslocar em atraso uma fun¸ao no tempo de t0 segundos significa atrasar a
c˜
fase do seu espectro de ωt0 rad para cada valor da frequˆncia ω.
e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-114-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 115
5.4.6 Diferencia¸˜o e Integra¸˜o no Tempo
ca ca
De maneira similar ` transformada de Laplace podemos relacionar as transformadas
a
de Fourier de uma fun¸˜o e de sua derivada (ou integral).
ca
Se F[f (t)] = F (ω) ent˜o:
a
df (t)
F[ ] = jωF (ω)
dt
e
t
1
F[ f (τ )dτ ] = F (ω) , se F (ω) = 0 para ω = 0
−∞ jω
A restri¸˜o F (ω) = 0 para ω = 0 implica que o valor m´dio do sinal deve ser nulo, isto
ca e
∞
´ −∞ f (t)dt = 0. Essa restri¸˜o pode ser eliminada mas a express˜o acima se torna mais
e ca a
complicada. Para maiores detalhes veja, por exemplo [5].
Exemplo 5.6 Obtenha a Transformada de Fourier do sinal f (t) da figura 5.11.
f(t)
A
−b −a 0 a b t
Figura 5.11: Sinal linear por trechos
Solu¸˜o: Ao inv´s de calcular F[f (t)] diretamente vamos utilizar o fato que F[ dfdt ] =
ca e (t)
jωF (ω) onde F (ω) ´ a fun¸˜o que estamos procurando. A figura 5.12 mostra a derivada
e ca
da fun¸˜o na figura 5.11.
ca
df (t)
dt
A
b−a
a b
−b −a 0 t
A
− b−a
Figura 5.12: Derivada do sinal linear por trechos
Aplicando novamente a propriedade de deriva¸˜o temos: F[ dt [ dfdt ]] = jωF[ df ] =
ca d (t)
dt
(jω)2 F (ω). A figura 5.13 mostra a derivada segunda da fun¸˜o na figura 5.11.
ca
Pela figura 5.13 podemos ent˜o escrever:
a
d2 f A
2
= [δ(t + b) − δ(t + a) − δ(t − a) + δ(t − b)]
dt b−a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-115-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 116
d2 f (t)
dt2 A
A
δ(t + b) b−a
δ(t − b)
b−a
−a a
−b 0 b t
A
b−a
δ(t + a) A
δ(t − a)
b−a
Figura 5.13: Derivada segunda do sinal linear por trechos
como F[δ(t − t0 )] = e−jωt0 temos:
d2 f A 2A
F[ ]= [ejωb − ejωa − e−jωa + e−jωb ] = (cos(ωb) − cos(ωa))
dt2 b−a b−a
2
como F[ d 2 ] = (jω)2 F (ω) temos o resultado desejado:
dt
f
2A cos(ωa) − cos(ωb)
F (ω) =
b−a ω2
5.4.7 Diferencia¸˜o em Frequˆncia
ca e
Se F[f (t)] = F (ω) ent˜o:
a
dF (ω)
F[tf (t)] = j
dω
5.4.8 Convolu¸˜o
ca
Usaremos a seguinte nota¸˜o para a Integral de Convolu¸ao entre dois sinais:
ca c˜
∞
f1 (t) ∗ f2 (t) = f1 (τ )f2 (t − τ )dτ
−∞
Analogamente ` transformada de Laplace podemos transformar a integral de con-
a
volu¸a˜ em produto no dom´
c o ınio da frequˆncia. Seja F[f1 (t)] = F1 (ω) e F[f2 (t)] = F2 (ω)
e
ent˜o:
a
F[f1 (t) ∗ f2 (t)] = F1 (ω)F2 (ω)
A prova desse resultado ´ bastante simples.
e
∞ ∞
F[f1 (t) ∗ f2 (t)] = f1 (τ )f2 (t − τ )dτ e−jωt dt
−∞ −∞
∞ ∞
= f1 (τ ) f2 (t − τ )e−jωt dt dτ
−∞ −∞](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-116-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 117
∞
como −∞
f2 (t − τ )e−jωt dt = F2 (ω)e−jωτ temos o resultado desejado:
F[f1 (t) ∗ f2 (t)] = F1 (ω)F2 (ω)
´
E importante n˜o confundir a nota¸ao para integral de convolu¸˜o, aqui representada
a c˜ ca
pelo s´
ımbolo (*) com a nota¸ao de produto usual de sinais. Veja a diferen¸a:
c˜ c
F[f1 (t) ∗ f2 (t)] = F1 (ω)F2 (ω)
1
F[f1 (t)f2 (t)] = F1 (ω) ∗ F2 (ω) (5.18)
2π
Problema 5.3 Obtenha a propriedade da modula¸˜o pela propriedade (5.18) acima.
ca
As transformadas de Fourier e Laplace s˜o ferramentas muito importantes e sob certas
a
condi¸˜es podem ser usadas indistintamente. No entanto, Laplace ´ adequada ` an´lise
co e a a
de sistemas1 por permitir o tratamento das condi¸˜es iniciais do mesmo, al´m de poder
co e
tratar sistemas inst´veis. J´ Fourier ´ adequado ` an´lise de sinais devido ` interpreta¸ao
a a e a a a c˜
frequencial que se pode dar ao espectro do sinal, como por exemplo na modula¸ao de c˜
sinais. .
Exemplo 5.7 Calcule a resposta ao degrau unit´rio do filtro abaixo por Laplace e Fourier.
a
1
Suponha que a fun¸˜o de transferˆncia do filtro seja F (s) = s+1 e lembre que Y (s) =
ca e
F (s)X(s), y(t) = f (t) ∗ x(t) e f (t) = L−1 [F (s)].
X(s) Y(s)
F(s)
x(t) y(t)
f(t)
1
Figura 5.14: Filtro de primeira ordem com F (s) = s+1
1
Solu¸˜o: Por Laplace: O sinal de entrada ´ um degrau unit´rio, logo X(s) =
ca e a s
e assim
temos:
1 1 −1 1
Y (s) = F (s)X(s) = = +
s+1s s+1 s
⇒ y(t) = L−1 [Y (s)] = 1 − e−t , t ≥ 0
Por Fourier: Note que y(t) = x(t) ∗ f (t) ⇒ Y (ω) = X(ω)F (ω). A transformada do
sinal de entrada ´
e
1
X(ω) = F[x(t)] = + πδ(ω)
jω
Para obter a transformada F (ω) note que a regi˜o de convergˆncia de F (s) cont´m o eixo
a e e
imagin´rio. Logo F (ω) = F (s)|s=jω .
a
1
descritos por equa¸˜es diferenciais lineares invariantes no tempo
co](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-117-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 118
Da´ obtemos:
ı
1 1
Y (ω) = + πδ(ω)
jω + 1 jω
1 1 π
= + δ(ω)
jω + 1 jω jω + 1
Por fra¸˜es parciais temos
co
1 1 −1 1
= +
jω + 1 jω jω + 1 jω
π
Como jω+1
δ(ω) = πδ(ω) conclu´mos:
ı
−1 1
Y (ω) = + + πδ(ω)
jω + 1 jω
Logo:
−1 1
y(t) = F −1 [Y (ω)] = F −1 + F −1 + πδ(ω)
jω + 1 jω
= −e−t + 1, t ≥ 0
Note que apesar da abordagem por Laplace ser mais simples, Laplace e Fourier fornecem
o mesmo resultado para a resposta for¸ada do filtro. No entanto n˜o seria poss´ aplicar
c a ıvel
Fourier para analisar a resposta livre do filtro, j´ que essa transformada n˜o permite o
a a
tratamento de condi¸oes iniciais.
c˜
Problema 5.4 Podemos representar matematicamente a intera¸˜o entre dois sinais f1 (t), f2 (t)
ca
atrav´s da convolu¸˜o desses dois sinais f1 (t) ∗ f2 (t). Encontre condi¸˜es para os espec-
e ca co
tros desses sinais F1 (ω), F2 (ω) de tal forma que n˜o exista intera¸˜o entre f1 (t), f2 (t),
a ca
isto ´ f1 (t) ∗ f2 (t) = 0. Nesses casos dizemos que n˜o existe interferˆncia de f1 (t) sobre
e a e
f2 (t) e vice-versa.
5.4.9 Amostragem
O problema que estudaremos a seguir consiste na determina¸ao de condi¸oes para se
c˜ c˜
amostrar um sinal sem perda de informa¸ao. Este problema ´ muito importante pois
c˜ e
todo sinal armazenado ou processado nos computadores ´ antes digitalizado, isto ´, o
e e
sinal ´ amostrado e suas amostras s˜o transformadas em c´digo bin´rio para depois ser
e a o a
processado ou armazenado em computadores. A transmiss˜o digital de sinais tamb´m
a e
passa pelo mesmo processo de amostragem e codifica¸ao, por´m ´ importante que o
c˜ e e
sinal original possa ser reconstru´
ıdo, a partir do digital transmitido. Torna-se ent˜o
a
imperativo saber a frequˆncia de amostragem do sinal para que, uma vez discretizado, se
e
possa reconstru´ a partir de suas amostras coletadas.
ı-lo
Problema a ser resolvido: Suponha um sistema de transmiss˜o digital ideal (sem ru´
a ıdo
nem erro de quantiza¸˜o) ilustrado na figura 5.15. Determine a frequˆncia de amostragem
ca e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-118-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 119
sinal a ser transmiss˜o
a sinal recebido
A/D ..... D/A
transmitido
amostragem e decodifica¸ao e
c˜
codifica¸ao
c˜ reconstru¸ao
c˜
Figura 5.15: Transmiss˜o e recupera¸˜o de sinais
a ca
de um sinal para que uma vez transmitido se possa reconstru´ exatamente como ele
ı-lo
era antes da amostragem.
Um solu¸ao para o problema acima ´ fornecida pelo teorema da amostragem enunciado
c˜ e
a seguir:
Um sinal limitado em frequˆncia, isto ´, cujo espectro ´ nulo acima de uma
e e e
frequˆncia ω (rad/s) ´ reconstru´do unicamente por suas amostras tomadas `
e ¯ e ı a
intervalos uniformes menores que
π
Ta = segundos
ω
¯
A seguir apresentaremos a demonstra¸ao do resultado acima.
c˜
O processo ideal de amostragem pode ser representado pelo produto do sinal f (t) a ser
amostrado por um trem de impulsos ocorrendo nos instantes de amostragem.
fs (t) = f (t)δTa (t)
onde fs (t) ´ o sinal amostrado e δTa (t) ´ o trem de impulsos cujo per´
e e ıodo ´ o pr´prio
e o
per´ıodo de amostragem. O processo de amostragem assim representado ´ ideal porque a
e
coleta de uma amostra leva um tempo infenitesimal, que ´ o tempo de dura¸˜o de um
e ca
impulso. O valor da amostra coletada ´ a ´rea do impulso e corresponde ao valor exato
e a
do sinal no instante onde ocorre o impulso. Na pr´tica n˜o podemos implementar tal
a a
processo de amostragem. Por´m boas aproxima¸oes podem ser obtidas substituindo-se
e c˜
os impulsos por pulsos de largura bem pequena e amplitude unit´ria.
a
O espectro do sinal amostrado ´ ent˜o:
e a
1
Fs (ω) = F[fs (t)] = F[f (t)δTa (t)] = F[f (t)] ∗ F[δTa (t)]
2π
De um exemplo anterior vimos que F[δTa (t)] = ωa δωa (ω) onde ωa = 2π/Ta ´ a frequˆncia
e e
fundamental do trem de impulsos que corresponde ` frequˆncia de amostragem que quer-
a e
emos determinar. Logo, para F (ω) = F[f (t)] temos:
∞
1 1
Fs (ω) = F (ω) ∗ [ωa δωa ] = F (ω) ∗ δ(ω − nωa )
2π Ta n=−∞
∞ ∞
1 1
= F (ω) ∗ δ(ω − nωa ) = F (ω − nωa )
Ta n=−∞
Ta n=−∞](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-119-320.jpg)
![5.4. Propriedades da transformada www.das.ufsc.br/labsil 120
Como f (t) ´ um sinal limitado em frequˆncia, isto ´, existe ω tal que F (ω) = 0 para
e e e ¯
ω ≥ ω , vamos considerar as duas possibilidades seguintes:
¯
π
Caso ωa > 2¯ ou seja Ta <
ω ω
¯
segundos
Fs (ω)
F (ω)
A
A Ta
... ...
−¯
ω 0 ω
¯ ω −ωa 0 ωa ω
−¯
ω ω
¯ ωa − ω
¯
Figura 5.16: Espectro do sinal antes e ap´s amostragem: Caso ωa > 2¯
o ω
A figura 5.16 mostra o espectro F (ω) de um sinal fict´ f (t) e o espectro Fs (ω) desse
ıcio
sinal amostrado com frequˆncia de amostragem ωa sob a hip´tese de que ωa > 2¯ . Note
e o ω
que o espectro do sinal amostrado Fs (ω) cont´m o espectro do sinal original F (ω) sem
e
distor¸˜o, como pode ser visto entre as frequˆncias −¯ e ω . Assim, para recuperar o sinal
ca e ω ¯
original a partir do sinal amostrado basta eliminar todas as componentes de frequˆncia do
e
sinal Fs (ω) fora do intervalo [−¯ , ω ]. Esta opera¸˜o de filtragem est´ indicada na figura
ω ¯ ca a
5.17. Note que o filtro ideal anula todas as componentes de frequˆncia fora do intervalo
e
[−¯ , ω ] como indicado a seguir.
ω ¯
G(ω)
filtro ideal
Ta
Fs (ω) F (ω)
G(ω)
ω
−¯
ω ω
¯
Figura 5.17: Filtro ideal para recupera¸ao do sinal: Caso ωa > 2¯
c˜ ω
Fs (ω)G(ω) = F (ω)
No dom´
ınio do tempo a filtragem acima ´ dada pela convolu¸˜o:
e ca
f (t) = fs (t) ∗ g(t)
onde g(t) = F −1 [G(ω)] = Sa (¯ t). Este resultado pode ser obtido facilmente com (5.17) e
ω](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-120-320.jpg)

![5.4. Propriedades da transformada www.das.ufsc.br/labsil 122
teorema enunciado pressup˜e a utiliza¸˜o de um amostrador ideal (trem de impulsos) e de
o ca
um filtro ideal para reconstru¸˜o do sinal (filtro com espectro do tipo porta). Na pr´tica
ca a
n˜o podemos implementar nem o amostrador nem o filtro ideal. No entanto, podemos
a
implementar dispositivos de amostragem e filtros que se aproximam bastante do caso
ideal. Logo, n˜o teremos reconstru¸˜o perfeita na pr´tica mas sim uma reconstru¸˜o que
a ca a ca
ser´ t˜o melhor quanto mais o amostrador e o filtro se aproximarem do ideal.
a a
O teorema da amostragem parte da hip´tese de que o sinal a ser amostrado ´ limitado
o e
em frequˆncia, isto ´ seu espectro ´ nulo a partir de uma certa frequˆncia (¯ ). Na pr´tica
e e e e ω a
o espectro dos sinais n˜o s˜o nulos a partir de uma certa frequˆncia mas sim muito
a a e
pequenos a partir de uma certa frequˆncia. Logo o erro de aproxima¸ao de um sinal
e c˜
pr´tico por um sinal limitado em frequˆncia pode ser feito bastante pequeno. Para isso
a e
devemos escolher adequadamente a frequˆncia (¯ ) a partir da qual iremos considerar nulo
e ω
(truncar) o espectro do sinal. Em geral, quanto maior essa frequˆncia de truncamento
e
menor o erro cometido. Entretanto, quanto maior a frequˆncia de truncamento mais
e
r´pido deve ser o processo de amostragem (ωa > 2¯ ) o que torna o dispositivo mais caro.
a ω
Exemplo 5.8 Utilize o teorema da amostragem para determinar a frequˆncia de dis-
e
cretiza¸˜o do sinal f (t) = cos(100πt) + sen(10πt).
ca
Solu¸˜o: Com a transformada de Fourier podemos calcular o espectro do sinal. Ele
ca
est´ ilustrado na figura 5.19.
a
F (ω)
jπ δ(ω + 10π) π δ(ω − 100π)
π δ(ω + 100π)
ω
jπ δ(ω − 10π)
Figura 5.19: Espectro do sinal f (t) = cos(100πt) + sen(10πt).
F[cos100πt] = π[δ(ω − 100π) + δ(ω + 100π)]
F[sen10πt] = jπ[δ(ω + 10π) − δ(ω − 10π)]
como F (ω) = 0 para ω > 100π temos ω = 100π. Logo:
¯
ωa > 2¯ = 200π
ω
Exemplo 5.9 Com o aux´lio do teorema da amostragem determine a resposta y(t) do
ı
sistema indicado na figura 5.20 para o seguinte sinal de entrada x(t) = Sa (50πt).
Solu¸˜o: O espectro do sinal de entrada est´ indicado na figura 5.21(a) e pode ser
ca a
calculado com (5.17) da seguinte forma.
π 1
X(ω) = F[Sa (50πt)] = G100π (ω) = G100π (ω)
50π 50](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-122-320.jpg)




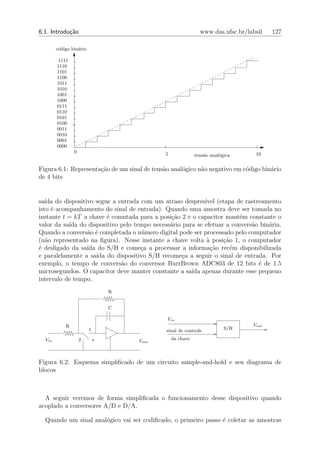
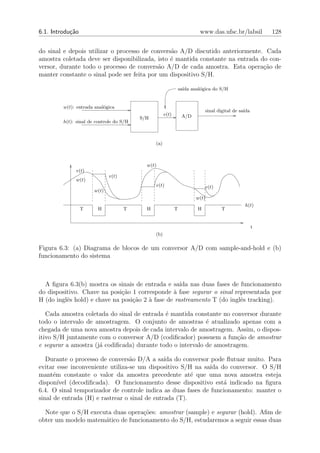

![6.1. Introdu¸˜o
ca www.das.ufsc.br/labsil 130
r∗ (t) rh (t)
ZOH
r(kT )
r(kT )δ(t − kT )
kT t kT kT+T t
sinal amostrado (entrada) sinal constante por trechos (sa´
ıda)
Figura 6.6: Segurador de ordem zero: a sa´ ´ constante por trechos
ıda e
ıfico do sinal rh (t) obtido com r∗ (t) = δ(t). Pela figura 6.6 deduzimos que
´ o valor espec´
e
a resposta impulsional vale
rh (t) = zoh(t) = 1 para 0 ≤ t < T (6.2)
que pode ser rescrita de uma forma mais conveniente com o aux´ da fun¸ao degrau
ılio c˜
unit´rio u(t) na forma
a
zoh(t) = u(t) − u(t − T ) (6.3)
A fun¸˜o de transferˆncia ZOH(s) do bloco ZOH pode ent˜o ser calculada com o aux´
ca e a ılio
da transformada de Laplace
1 e−sT
ZOH(s) = L[zoh(t)] = − (6.4)
s s
Assim conclu´
ımos que o dispositivo S/H pode ser representado por um amostrador ideal
em cascata com um segurador de ordem zero como ilustra a figura 6.7.
r(t) rh (t) r(t) r∗ (t) rh (t)
S/H ≡ ZOH
T
Figura 6.7: Sample-and-Hold visto como um amostrador ideal em cascata com um segu-
rador de ordem zero
´
E importante notar que o amostrador ideal n˜o pode ser implementado na pr´tica
a a
devido ` presen¸a de impulsos no sinal amostrado. No entanto a representa¸ao do dis-
a c c˜
positivo S/H indicada na figura 6.7 possui duas propriedades interessantes: (i) existem
dispositivos S/H cujos comportamentos entrada/sa´ s˜o similares ao acima descrito
ıda a
e (ii) o segurador de ordem zero pode ser tratado de maneira muito conveniente pela
Transformada Z, como veremos mais tarde.
Um outro ponto importante a ser notado ´ que no controle de sistemas normalmente se
e
assume a priori, por raz˜es de simplicidade, que o erro de convers˜o bin´ria ´ despres´
o a a e ıvel.
Isso implica que o conversor A/D pode ser representado por um amostrador ideal e o
conversor D/A por um segurador de ordem zero. Essas hip´teses s˜o comuns em todos os
o a
livros cl´ssicos de controle e tamb´m ser˜o assumidas nesse cap´
a e a ıtulo sempre que houver
conversores A/D e D/A presentes na malha de controle.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-130-320.jpg)

![6.2. Sinais e Sistemas de Tempo Discreto www.das.ufsc.br/labsil 132
Sistemas cont´nuos s˜o aqueles que manipulam sinais anal´gicos e s˜o representados por
ı a o a
equa¸˜es diferenciais, como ´ o caso do sistema na figura 6.8. Sistemas discretos s˜o
co e a
aqueles que manipulam sequˆncias e s˜o representados por equa¸˜es recursivas, como ´
e a co e
o caso do sistema representado pela equa¸˜o recursiva 6.5. Note que o sistema discreto
ca
n˜o ´ equivalente ao sistema cont´nuo que lhe deu origem pois apesar dos dois sistemas
a e ı
representarem o comportamento exato da corrente no circuito nos instantes t = kT ,
apenas o sistema cont´nuo pode fornecer o valor exato da corrente para todo instante de
ı
tempo t ≥ 0. Al´m disso, o sistema discreto descrito pela equa¸˜o recursiva 6.5 pode ser
e ca
interpretado como um algor´tmo cuja evolu¸˜o define a dinˆmica da corrente do circuito
ı ca a
RC nos instantes t = kT .
Exemplo 6.2 Obtenha a equa¸˜o recursiva que rege o comportamento dinˆmico do cir-
ca a
cuito da figura 6.10 nos instantes t = kT sendo T um intervalo de tempo dado, k =
0, 1, 2, . . . uma vari´vel discreta e e(t) constante por trechos, isto ´, e(t) = e(kT ) para
a e
kT ≤ t < kT + T .
R
+ +
e(t) C x(t)
- -
Figura 6.10: Circuito RC com entrada constante por trechos
Solu¸˜o: Para kT ≤ t < kT + T a dinˆmica do circuito ´ dada por:
ca a e
RC x + x = e(kT ),
˙ x(t0 ) = x(kT )
Como e(kT ) ´ constante no intervalo temos:
e
e(kT )
RC[sX(s) − x(kT )] + X(s) =
s
Logo:
e(kT ) 1 e(kT ) + sRCx(kT )
X(s) = + RCx(kT ) =
s RCs + 1 s(RCs + 1)
e(kT ) x(kT ) − e(kT )
= +
s s + 1/RC
Usando a Transformada Inversa e lembrando que o lado direito da equa¸˜o acima
ca
possui instante inicial t0 = kT temos:
t−kT
x(t) = e(kT ) + (x(kT ) − e(kT ))e− RC , kT ≤ t < kT + T
Como x(t) ´ uma fun¸˜o cont´nua temos pela express˜o acima que o valor de x(kT +T )
e ca ı a
´ dado por:
e
x(kT + T ) = lim x(t) = e(kT ) + (x(kT ) − e(kT ))e−T /RC
t→kT +T](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-132-320.jpg)


![6.3. Transformada Z www.das.ufsc.br/labsil 135
6.3.1 Defini¸˜o e exemplos
ca
A transformada Z de uma sequˆncia x(kT ) que satisfaz x(kT ) = 0 para k < 0, ´
e e
definida pela express˜o:
a
∞
X(z) = Z[x(kT )] = x(kT )z −k ; x(kT ) = 0, ∀ k < 0 (6.6)
k=0
onde z = α+jβ ´ uma vari´vel complexa similar ` vari´vel s da transformada de Laplace.
e a a a
Assim, a transformada Z transforma uma sequˆncia x(kT ) numa fun¸ao X(z) da vari´vel
e c˜ a
complexa z. Veremos mais tarde que podemos relacionar a fun¸ao X(z) com a fun¸˜o
c˜ ca
X(s) da transformada de Laplace do sinal x(t) amostrado nos instantes t = kT .
Note que a transformada Z ´ definida como sendo a soma dos termos de uma s´rie na
e e
vari´vel complexa z, pois pela defini¸ao temos
a c˜
X(z) = x(0) + x(T )z −1 + x(2T )z −2 + . . .
Al´m disso, os coeficientes dessa s´rie s˜o os valores que o sinal assume nos diversos
e e a
instantes discreto de tempo. O valor do sinal x(t) no instante t = kT aparece na s´rie
e
−k
como o coeficiente do termo z .
Em alguns casos, quando a s´rie ´ geom´trica e de raz˜o r conhecida, podemos calcular
e e e a
o resultado da soma atrav´s da f´rmula
e o
x(0)
x(z) = x(0) + x(T )z −1 + x(2T )z −2 + · · · = (6.7)
1−r
Para que o resultado da soma da s´rie seja dado pela f´rmula acima ´ preciso que a s´rie
e o e e
seja convergente, isto ´ a raz˜o da s´rie deve possuir m´dulo menor que a unidade |r| < 1.
e a e o
Veja o exemplo a seguir.
Exemplo 6.3 Calcule a transformada Z da sequˆncia degrau unit´rio (u(kT )) definida
e a
como u(kT ) = 1 para k ≥ 0 e u(kT ) = 0 para k < 0.
Solu¸˜o: Pela defini¸˜o temos:
ca ca
∞ ∞
−k
Z[u(kT )] = u(kT )z = z −k = 1 + z −1 + z −2 + . . .
k=0 k=0
A s´rie acima possui raz˜o r = z −1 e a soma dos termos dessa s´rie ´ dada por 6.7
e a e e
−1
desde que a vari´vel complexa z esteja na regi˜o onde |r| = |z | < 1. Nessas condi¸˜es
a a co
temos:
1 z
U (z) = Z[u(t)] = −1
=
1−z z−1
Analogamente ` Transformada de Laplace e Fourier, a Transformada Z tamb´m possui
a e
uma regi˜o de convergˆncia. Uma s´rie ´ convergente se em m´dulo a raz˜o ´ menor que
a e e e o a e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-135-320.jpg)
![6.3. Transformada Z www.das.ufsc.br/labsil 136
Im[z] Im[s]
c´
ırculo unit´rio
a
1
Re[z] Re[s]
0
Plano z Plano s
transformada Z transformada de Laplace
1
z U (s) = s
U (z) = z−1
Figura 6.13: Regi˜o de convergˆncia das transformadas do degrau unit´rio
a e a
a unidade. Para o caso do degrau unit´rio a regi˜o de convergˆncia ´ |z −1 | < 1 que no
a a e e
plano z define a regi˜o externa ao c´rculo unit´rio como ilustra a figura 6.13. Dentro da
a ı a
regi˜o de convergˆncia a sequˆncia u(kT ) e sua Transformada Z est˜o relacionadas de
a e e a
maneira biun´voca como ilustra a figura 6.14.
ı
Z[x(kT )]
x(kT ) X(z)
(k ≥ 0) z ∈ Rconv
Z −1 [X(z)]
Figura 6.14: Rela¸˜o biun´
ca ıvoca entre a sequˆncia x(kT ) e sua transformada Z
e
A existˆncia de uma regi˜o de convergˆncia para a Transformada, seja Laplace, Fourier
e a e
ou Z, ´ um dado importante, pois caso contr´rio a Transformada em quest˜o deixa de ter
e a a
sentido. No entanto, calcular essa regi˜o de convergˆncia ´ algo irrelevante, pois se existe
a e e
uma regi˜o de convergˆncia, existe uma fun¸ao X(s), X(jω) ou X(z) conforme o caso.
a e c˜
Dentro da regi˜o de convergˆncia a Transformada e a respectiva fun¸ao temporal est˜o
a e c˜ a
diretamente relacionadas. Fora da regi˜o de convergˆncia, a Transformada pode ser vista
a e
como uma fun¸ao auxiliar que cont´m informa¸˜es relevantes sobre a fun¸ao no dom´
c˜ e co c˜ ınio
do tempo, mesmo n˜o estando diretamente relacionadas.
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-136-320.jpg)
![6.3. Transformada Z www.das.ufsc.br/labsil 137
6.3.2 Rela¸˜o com a transformada de Laplace
ca
Podemos facilmente relacionar a vari´vel complexa z da transformada Z com a vari´vel
a a
s da transformada de Laplace.
Vamos supor que x(t) seja um sinal anal´gico dado e que
o
∞
x∗ (t) = x(kT )δ(t − kT )
k=0
seja a representa¸ao do sinal x(t) amostrado com amostrador ideal (veja figura 6.5). Note
c˜
que a representa¸˜o do sinal amostrado x∗ (t) ´ diferente da representa¸ao da sequˆncia
ca e c˜ e
x(kT ) obtida com os valores de x(t) nos instantes t = kT . Enquanto x∗ (t) ´ um sinal
e
anal´gico com impulsos, a sequˆncia x(kT ) ´ um sinal discreto.
o e e
Tomemos agora a Transformada de Laplace da express˜o acima:
a
∞
∗ ∗
L[x (t)] = X (s) = x(kT )e−kT s , x(t) = 0, t < 0
k=0
Considerando a mudan¸a de vari´vel
c a
z = eT s (6.8)
podemos reescrever X ∗ (s) em termos da vari´vel z como indicado a seguir.
a
∞
∗ ∗
X (s)|s= ln(z) = Z[x (t)] = x(kT )z −k ; x(kT ) = 0, ∀ k < 0 (6.9)
T
k=0
Comparando (6.9) com (6.6) conclu´ ımos que a mudan¸a de vari´vel (6.8) define a rela¸˜o
c a ca
∗
entre a vari´vel s da transformada de Laplace do sinal amostrado x (t) e a vari´vel z da
a a
transformada Z da sequˆncia x(kT ).
e
Veja por exemplo a rela¸˜o que existe entre os p´los da transformada Z e Laplace do
ca o
degrau unit´rio indicadas na figura 6.13. O p´lo da transformada de Laplace est´ na
a o a
origem s = 0. O p´lo da transformada Z est´ em z = 1. Este mapeamento de s = 0 em
o a
Laplace para z = 1 no plano Z ´ dado pela equa¸ao (6.8).
e c˜
Exemplo 6.4 (Fun¸˜o Potˆncia) Calcule a transformada Z da fun¸˜o potˆncia ak
ca e ca e
onde a ´ uma constante e k ≥ 0 ´ uma vari´vel discreta.
e e a
Solu¸˜o: Com (6.7) temos:
ca
∞
1 z
Z[ak u(k)] = ak z −k = =
k=0
1 − a z −1 z−a
Como curiosidade, a regi˜o de convergˆncia da transformada ´ Rconv = {z : |a z −1 | <
a e e
1 }. Note ainda que com o resultado acima podemos facilmente obter a transformada Z
da fun¸˜o exponencial f (k) = ebk onde b ´ uma constante e k ≥ 0 ´ uma vari´vel discreta
ca e e a
(verifique !).](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-137-320.jpg)
![6.4. Propriedades da Transformada Z www.das.ufsc.br/labsil 138
Exemplo 6.5 (Fun¸˜o Senoidal) Calcule a transformada Z da fun¸˜o senoidal sen(ω0 kT )
ca ca
onde ω0 e T s˜o constantes e k ≥ 0 ´ uma vari´vel discreta.
a e a
Solu¸˜o: Aplicando a defini¸˜o e f´rmula de Euler temos:
ca ca o
∞ ∞
−k ejω0 kT − e−jω0 kT −k
Z[sen(ω0 kT )u(kT )] = sen(ω0 kT )z = z
k=0 k=0
2j
∞
1
= ejω0 kT z −k − e−jω0 kT z −k
2j k=0
1 z z
= jω0 T
−
2j z − e z − e−jω0 T
z sen(ω0 T )
= 2
z − 2 z cos(ω0 T ) + 1
Exemplo 6.6 (Pulso Unit´rio) Calcule a transformada Z da fun¸˜o Pulso Unit´rio:
a ca a
δ(k) definida como δ(k) = 1 para k = 0 e nula para k = 0.
Solu¸˜o: Aplicando a defini¸˜o encontramos
ca ca
∞
Z[δ(k)] = δ(k)z −k = 1
k=0
Para a fun¸˜o pulso deslocada no instante k = m, definida como δ(k − m) = 1 para
ca
k = m e nula para k = m encontramos
∞
Z[δ(k − m)] = δ(k − m)z −k = z −m
k=0
As figuras 6.15, 6.16 e 6.17 ilustram a rela¸ao entre a localiza¸ao dos p´los da trans-
c˜ c˜ o
formada Z do sinal e o seu comportamento temporal.
6.4 Propriedades da Transformada Z
6.4.1 Linearidade
A Transformada Z ´ uma opera¸ao linear, isto ´,
e c˜ e
Z[α1 x(k) + α2 y(k)] = α1 Z[x(k)] + α2 Z[y(k)]
para todo α1 , α2 ∈ C.
Problema 6.2 Prove que a transformada Z ´ uma opera¸˜o linear
e ca](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-138-320.jpg)
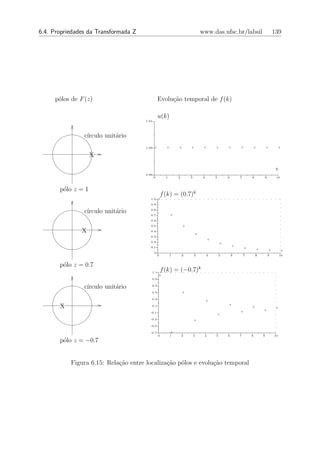
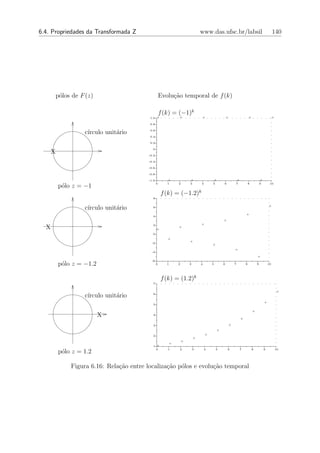
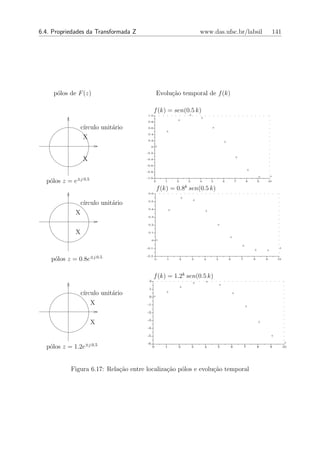
![6.4. Propriedades da Transformada Z www.das.ufsc.br/labsil 142
6.4.2 Teorema do Valor Inicial
Se Z[x(k)] = X(z) e limz→∞ X(z) existe ent˜o:
a
x(0) = lim X(z).
z→∞
∞
Prova: Note que Z[x(k)] = k=0 x(k)z −k = x(0) + x(1)z −1 + . . .
Logo, quando z → ∞ obtem-se o resultado desejado.
6.4.3 Teorema do Valor Final
Se Z[x(k)] = X(z) e se a fun¸˜o (z − 1)X(z) ´ anal´
ca e ıtica sobre e fora do c´
ırculo unit´rio,
a
ent˜o:
a
lim x(k) = lim (z − 1)X(z)
k→∞ z→1
Prova: Note que
∞
Z[x(k)] = X(z) = x(k)z −k
k=0
∞
Z[x(k + 1)] = zX(z) − zx(0) = x(k + 1)z −k
k=0
Tomando a diferen¸a entre as duas express˜es acima:
c o
∞
[x(k + 1) − x(k)]z −k = zX(z) − zx(0) − X(z) = (z − 1)X(z) − zx(0)
k=0
Supondo que a sequˆncia x(k) converge para um valor finito em regime, temos que X(z)
e
pode ter no m´ximo um p´lo sobre o c´
a o ırculo unit´rio e nenhum p´lo fora dele (veja figuras
a o
6.15-6.17). Isso implica que a fun¸˜o auxiliar (z − 1)X(z) n˜o pode ter p´los sobre nem
ca a o
fora do c´
ırculo unit´rio, ou seja devem estar dentro do c´
a ırculo unit´rio. Logo para z → 1
a
temos o seguinte resultado:
∞
lim [x(k + 1) − x(k)]z −k = lim [(z − 1)X(z) − zx(0)]
z→1 z→1
k=0
de onde se conclui que no limite ficamos com
∞
x(k + 1) − x(k) = lim [(z − 1)X(z)] − x(0)
z→1
k=0
x(∞) − x(0) = lim (z − 1)X(z) − x(0)
z→1
⇒ x(∞) = lim (z − 1)X(z)
z→1
que ´ o resultado desejado.
e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-142-320.jpg)
![6.4. Propriedades da Transformada Z www.das.ufsc.br/labsil 143
6.4.4 Obten¸˜o de F (z) a partir de F (s)
ca
Vimos anteriormente que existe uma rela¸˜o entre a transformada de Laplace de um
ca
∗
sinal x (t) amostrado nos instantes t = kT e a transformada Z da sequˆncia x(kT ).
e
Dessa rela¸ao podemos montar tabelas que relacionam X(s) (a transformada de Laplace
c˜
do sinal x(t)) e a respectiva transformada Z da sequˆncia x(kT ). A figura 6.18 ilustra
e
essa rela¸ao.
c˜
sinal discreto
f (kT )
Z[f (kT )]
amostrador ideal
L−1 [F (s)] L[f ∗ (kT )]
f (t) f ∗ (kT ) ln(z)
F (s) s= T F (z)
T sinal amostrado
Z[F (s)]
Tabelas ou Teorema dos Res´
ıduos
Figura 6.18: Obten¸ao de F (z) a partir de F (s)
c˜
As fun¸oes mais usuais j´ se encontram tabeladas em termos de suas Transformadas
c˜ a
Z, Laplace e Fourier. Logo o uso de tabelas associado ao m´todo de expans˜o em fra¸oes
e a c˜
parciais pode ser util na determina¸ao de F (z) a partir de F (s).
´ c˜
No entanto o uso de tabelas pode apresentar limita¸oes em alguns casos. A seguir
c˜
apresenta-se um procedimento anal´
ıtico alternativo bastante simples conhecido como
m´todo dos res´
e ıduos.
Sejam P1 , . . . , Pn o conjunto de p´los distintos de F (s). Caso F (s) possua p´los repeti-
o o
dos inclua o p´lo apenas uma vez no conjunto.
o
Ent˜o, com F (s) e P1 , . . . , Pn podemos calcular F (z) da seguinte forma:
a
n
F (z) = R(Pi )
i=1
sendo R(Pi ) o res´
ıduo do p´lo Pi (i = 1...n) dados por:
o
• P´lo simples (multiplicidade 1)
o
z
R(Pi ) = (s − Pi )F (s)
z − esT s=Pi](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-143-320.jpg)
![6.4. Propriedades da Transformada Z www.das.ufsc.br/labsil 144
• P´lo m´ltiplo (multiplicidade m)
o u
1 dm−1 z
R(Pi ) = m−1
(s − Pi )m F (s)
(m − 1)! ds z − esT s=Pi
O resultado acima ´ apresentado como exerc´ resolvido no livro do Ogata [1] (edi¸˜o
e ıcio ca
1982) ou ainda em v´rios outros livros sobre controle de sistemas a tempo discreto.
a
1
Exemplo 6.7 Obtenha F (z) = Z[F (s)] dado F (s) = (s+a)(s+b)
.
Solu¸˜o: Como F (s) possui dois p´los distintos temos:
ca o
F (z) = R(P1 ) + R(P2 )
sendo:
z
R(P1 ) = (s + a)F (s) z−esT s=−a
= b−a z−ez−aT
1
z
R(P2 ) = (s + b)F (s) z−esT s=−b
= a−b z−ez−bT
1
Logo:
1 z z
F (z) = −aT
−
b−a z−e z − e−bT
O resultado pode ser conferido com o aux´lio de tabelas (verifique!).
ı
6.4.5 Convolu¸˜o Discreta
ca
De forma an´loga ` integral de convolu¸˜o para sistemas de tempo cont´
a a ca ınuo, podemos
definir convolu¸˜o para sistemas de tempo discreto atrav´s de um somat´rio.
ca e o
Tempo cont´
ınuo:
∞ ∞
x1 (t) ∗ x2 (t) = x1 (τ )x2 (t − τ )dτ = x2 (τ )x1 (t − τ )dτ
−∞ −∞
Tempo discreto:
∞ ∞
x1 (kT ) ∗ x2 (kT ) = x1 (nT )x2 (kT − nT ) = x2 (nT )x1 (kT − nT )
n=−∞ n=−∞
Normalmente temos x1 (t) = 0 e x2 (t) = 0 para t < 0 e nesses casos podemos tomar
t0 = 0 como limite inferior, tanto na integral como no somat´rio.
o
Com a Transformada de Laplace vimos que convolu¸ao no dom´ do tempo se trans-
c˜ ınio
forma em produto no dom´ ınio da frequˆncia. Mostraremos a seguir que isto tamb´m ´
e e e
verdade em rela¸ao ` convolu¸ao discreta e a Transformada Z .
c˜ a c˜
L[x1 (t) ∗ x2 (t)] = X1 (s)X2 (s) (Transf. Laplace - Tempo Cont´
ınuo)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-144-320.jpg)
![6.5. Transformada Z Inversa www.das.ufsc.br/labsil 145
Z[x1 (kT ) ∗ x2 (kT )] = X1 (z)X2 (z) (Transf. Z - Tempo Discreto)
Prova: Seja y(kT ) o resultado da convolu¸˜o discreta.
ca
y(kT ) = x1 (kT ) ∗ x2 (kT )
Pela defini¸ao da Transformada Z temos:
c˜
∞ ∞ ∞
−k
Z[y(kT )] = y(kT )z = x1 (nT )x2 (kT − nT ) z −k
k=0 k=0 n=0
Fazendo a mudan¸a de vari´vel m = k − n encontramos:
c a
∞ ∞
Z[y(kT )] = x1 (nT )x2 (mT )z −(m+n)
m=0 n=0
∞ ∞
−m
= x2 (mT )z x1 (nT )z −n
m=0 n=0
= X1 (z)X2 (z)
que ´ o resultado desejado.
e
Note que a convolu¸˜o de uma sequˆncia qualquer x1 (kT ) com um pulso unit´rio δ(kT )
ca e a
resulta na pr´pria sequˆncia x1 (kT ) pois, como j´ vimos Z[δ(kT )] = 1.
o e a
1 k=0
δ(kT ) = Pulso Unit´rio na Origem
a
0 k=0
∞
Z[δ(kT )] = δ(kT )z −k = 1
k=0
Logo:
Z[f (kT ) ∗ δ(kT )] = Z[f (kT )]Z[δ(kT )] = Z[f (kT )]
⇒ f (kT ) ∗ δ(kT ) = f (kT )
A fun¸˜o pulso unit´rio δ(kT ) tem (em rela¸ao a Transformada Z ) as mesmas pro-
ca a c˜
priedades que a fun¸˜o impulso unit´rio δ(t) tem em rela¸˜o ` Transformada de Laplace
ca a ca a
.
6.5 Transformada Z Inversa
Existem basicamente trˆs m´todos para a determina¸˜o da Transformada Z Inversa.
e e ca
Cada um possui caracter´ ısticas diferentes, vantagens e desvantagens. A seguir apre-
sentaremos os dois mais utilizados.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-145-320.jpg)

![6.6. Solu¸˜o de Equa¸oes recursivas
ca c˜ www.das.ufsc.br/labsil 147
Compara¸˜o
ca
Tempo cont´
ınuo Transformada de Laplace
x(t)
˙ L[x(t)] = sX(s) − x(0)
˙
Tempo discreto Transformada Z
x(kT + T ) Z[x(kT + T )] = zX(z) − zx(0)
Tabela 6.2: Compara¸ao entre L[x(t)] e Z[x(kT + T )]
c˜ ˙
6.5.2 M´todo das fra¸˜es parciais de X(z)/z
e co
Este m´todo ´ o an´logo da expans˜o por fra¸oes parciais da utilizado na obten¸ao da
e e a a c˜ c˜
transformada inversa de Laplace. Note apenas que ao inv´s de expandir F (z) por fra¸˜es
e co
parciais devemos expandir X(z)/z. Veja o exemplo que segue.
10z
Exemplo 6.9 Calcule a sequˆncia x(k) cuja transformada Z ´ X(z) =
e e (z−1)(z−2)
.
Solu¸˜o:Expandindo X(z)/z for fra¸˜es parciais temos
ca co
X(z) 10 A B
= = +
z (z − 1)(z − 2) z−1 z−2
10 10
onde A = |
z−2 z=1
= −10 e B = |
z−1 z=2
= 10.
Logo:
z z
X(z) = −10 + 10
z−1 z−2
z
Lembrando que Z[ak ] = z−a
temos:
x(k) = −10(1)k + 10(2)k , k = 0, 1, 2, . . .
6.6 Solu¸˜o de Equa¸˜es recursivas
ca co
Veremos a seguir como calcular Transformada Z de uma sequˆncia deslocada e a
e
utiliza¸˜o desse resultado na solu¸˜o de equa¸˜es recursivas.
ca ca co
Seja X(kT ) um sequˆncia e x(kT + T ) a sequˆncia deslocada de T segundos (k =
e e
0, 1, 2, . . . ).
Assim como a Transformada de Laplace nos permite resolver equa¸˜es diferenciais, a
co
Transformada Z nos permite resolver equa¸˜es recursivas. Veja a compara¸ao na tabela
co c˜
6.2.
Quando as condi¸oes iniciais s˜o nulas podemos concluir que derivar um sinal de tempo
c˜ a
cont´
ınuo corresponde a multiplicar sua transformada de Laplace por s, isto ´ sX(s).
e
Analogamente, deslocar (um passo ` frente) um sinal de tempo discreto corresponde `
a a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-147-320.jpg)
![6.6. Solu¸˜o de Equa¸oes recursivas
ca c˜ www.das.ufsc.br/labsil 148
multiplicar sua transformada Z por z, isto ´ zX(z). A vari´vel complexa s corresponde
e a
ao operador derivada no dom´ do tempo cont´
ınio ınuo e a vari´vel complexa z corresponde
a
ao operador deslocamento um passo ` frente no dom´
a ınio do tempo discreto.
Para provar essa propriedade da Transformada Z note que:
∞
Z[x(kT )] = x(kT )z −k , x(t) = 0 t < 0
k=0
∞ ∞
−k
Z[x(kT + T )] = x(kT + T )z = x(nT )z −(n−1) (n = k + 1)
k=0 n=1
Somando e subtraindo o termo zx(0) obtemos:
∞
Z[x(kT + T )] = z x(nT )z −n + zx(0) − zx(0)
n=1
∞
= z x(nT )z −n − zx(0)
n=0
= zZ[x(nT )] − zx(0)
que prova a propriedade desejada. Analogamente temos:
Z[x(kT + 2T )] = zZ[x(kT + T )] − zx(T )
= z[zZ[x(kT )] − zx(0)] − x(T )
= z 2 X(z) − z 2 x(0) − zx(T )
Podemos enfim generalizar a propriedade do deslocamento no tempo aplicando suces-
sivamente os resultados acima e obtemos ap´s m sucessivos deslocamentos:
o
Z[x(k + m)] = z m X(z) − z m x(0) − z m−1 x(1) − · · · − zx(m − 1) (6.11)
Como z corresponde ao operador deslocamento um passo ` frente no tempo a vari´vel z −1
a a
corresponde ao operador deslocamento um passo ` traz no tempo. Utilizando o mesmo
a
procedimento acima encontramos
Z[x(k − m)] = z −m X(z) (6.12)
Exemplo 6.10 Resolva a seguinte equa¸˜o recursiva:
ca
x(k + 2) + 3x(k + 1) + 2x(k) = 0, x(0) = 0, x(1) = 1
Solu¸˜o: Tomando a Transformada dos dois lados e usando a linearidade temos:
ca
Z[x(k + 2)] + 3Z[x(k + 1)] + 2Z[x(k)] = 0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-148-320.jpg)
![6.6. Solu¸˜o de Equa¸oes recursivas
ca c˜ www.das.ufsc.br/labsil 149
com a propriedade de deslocamento encontramos:
z 2 X(z) − z 2 x(0) − zx(1) + 3[zX(z) − zx(0)] + 2X(z) = 0
z z z z
⇒ X(z) = = = −
z 2 + 3z + 2 (z + 2)(z + 1) z+1 z+2
z
Como Z[ak ] = z−a
obtemos:
x(k) = (−1)k − (−2)k , k = 0, 1, 2, . . .
Note que os p´los da Transformada X(z) se tornam a base das exponenciais no tempo.
o
Logo uma sequˆncia x(kT ) ´ convergente, x(k) tende assintoticamente ` zero quando
e e a
k → ∞, se todos os p´los da sua transformada X(z) s˜o em m´dulo inferiores ` unidade.
o a o a
Confirme esse resultado na figuras 6.15-6.17.
Im[z]
sequˆncias convergentes: |p´los| < 1
e o
X
X
Re[z] sequˆncias n˜o amortecidas: |p´los| = 1
e a o
X
sequˆncias divergentes: |p´los| > 1
e o
PLANO z
Figura 6.19: Sequˆncias convergentes e a localiza¸ao dos p´los no plano z
e c˜ o
Note que no caso da sequˆncia x(kT ) = sen(ω0 kT )u(kT ) sua transformada:
e
1 z z
X(z) = jω0 T
−
2j z − e z − e−jω0 T
possui dois p´los (z = e−jω0 T e z = ejω0 T ) que s˜o complexos conjugados (z = cos(ω0 T ) ±
o a
jsen(ω0 T )) e possuem m´dulo unit´rio indicando que a s´rie ´ oscilat´ria sem amorteci-
o a e e o
mento.
Exemplo 6.11 Determine a resposta do sistema descrito pela seguinte equa¸˜o recur-
ca
siva:
x(k + 2) − 3x(k + 1) + 2x(k) = u(k)
onde u(k) ´ o pulso unit´rio e x(k) = 0 para k ≤ 0.
e a
Solu¸˜o: Para resolver a equa¸˜o acima precisamos das condi¸˜es iniciais x(0) e x(1).
ca ca co
O valor de x(0) = 0 ´ dado e o valor de x(1) = 0 se obt´m da pr´pria equa¸˜o recursiva
e e o ca
com k = −1. Al´m disso, com a Transformada Z encontraremos:
e
z 2 X(z) − 3zX(z) + 2X(z) = U (z)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-149-320.jpg)
![6.6. Solu¸˜o de Equa¸oes recursivas
ca c˜ www.das.ufsc.br/labsil 150
A transformada do pulso unit´rio j´ calculamos anteriormente e vale U (z) = Z[u(k)] = 1.
a a
Logo:
1 −1 1
X(z) = 2 = +
z − 3z + 2 z−1 z−2
Como Z[x(k + 1)] = zX(z) − zx(0) e x(0) = 0 temos:
−z z
Z[x(k + 1)] = zX(z) = +
z−1 z−2
z
Lembrando que Z[ak ] = z−a
obtemos finalmente:
x(k + 1) = −(1)k + (2)k , k = 0, 1, 2, . . .
Exemplo 6.12 J´ vimos no exemplo 6.2 que no circuito RC da figura 6.10 onde e(t) ´
a e
constante por trechos (e(t) = e(kT ), kT ≤ t ≤ kT + T ) os sinais de entrada e sa´ nos
ıda
instantes t = kT s˜o dados pela equa¸˜o recursiva:
a ca
x(KT + T ) − a x(kT ) = b e(kT )
a = e−T /RC , b = 1 − e−T /RC
Obtenha a sequˆncia de sa´da x(kT ) para um degrau unit´rio aplicado na entrada.
e ı a
−T /RC
Suponha os dados e = 0.5 e x(0) = 0.
Solu¸˜o: Com a Transformada Z temos:
ca
Z[x(kT + T )] − aZ[x(kT )] = bZ[e(kT )]
zX(z) − zx(0) − aX(z) = bE(z)
z
Como E(z) = z−1
temos:
z0.5 −z z
X(z) = = +
(z − 0.5)(z − 1) z − 0.5 z − 1
z
Lembrando que Z[ak ] = z−a
encontramos:
x(kT ) = −(0.5)k + (1)k , k = 0, 1, 2, . . .
Note que a tens˜o em regime permanente se obt´m pelo limite:
a e
lim x(kT ) = 1, (Sistema Est´vel)
a
k→∞
Analogamente a tens`o inicial se obt´m:
a e
lim x(kT ) = 0
k→0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-150-320.jpg)

![6.7. Fun¸˜o de Transferˆncia Discreta e Estabilidade
ca e www.das.ufsc.br/labsil 152
Solu¸˜o: Tomando a Transformada Z da equa¸˜o recursiva temos:
ca ca
zX(z) − zx(0) − aX(z) = bE(z)
⇒ X(z) = F (z)E(z) + F0 (z)x(0)
b z
onde F (z) = z−a
e F0 (z) = z−a
.
Sejam f (k) = Z −1 [F (z)] e f0 (k) = Z −1 [F0 (z)]. Podemos ent˜o reescrever a express˜o
a a
acima da seguinte forma:
x(k) = Z −1 [X(z)] = Z −1 [F (z)E(z)] + Z −1 [F0 (z)]x(0)
= f (k) ∗ e(k) + f0 (k)x(0)
Note que f (k) e f0 (k) dependem apenas dos coeficientes constantes da equa¸˜o recur-
ca
siva. N˜o dependem nem da entrada, nem da sa´da nem das condi¸˜es iniciais.
a ı co
A parcela f (k) ∗ e(k), que ´ uma convolu¸˜o discreta e n˜o depende das condi¸˜es
e ca a co
iniciais, ´ a resposta de Estado Zero e a parcela f0 (k)x(0), que n˜o depende da entrada,
e a
´ a resposta de Entrada Zero.
e
Problema 6.3 Calcule as sequˆncias f (k) e f0 (k) do exemplo acima.
e
Se ao inv´s do circuito RC (de primeira Ordem) acima tomarmos a equa¸ao recursiva
e c˜
de um sistema gen´rico (6.13) obter´
e ıamos:
n−1
y(k) = f (k) ∗ x(k) + fi (k)ci (6.14)
i=0
onde ci = y(i) s˜o as condi¸˜es iniciais do sistema, f (k) e fi (k) s˜o sequˆncias que
a co a e
dependem apenas dos coeficientes da equa¸ao recursiva (6.13), x(k) ´ a sequˆncia de
c˜ e e
entrada e y(k) a de sa´
ıda.
Da express˜o acima observe que:
a
1. A sa´ de um sistema discreto depende dos parˆmetros f´
ıda a ısicos e do per´
ıodo de
amostragem que determinam os coeficientes da equa¸˜o recursiva e que por sua vez
ca
determinam as fun¸oes f (k) e fi (k) em (6.14).
c˜
2. A sa´ de um sistema discreto depende da entrada que lhe ´ aplicada e essa de-
ıda e
pendˆncia se expressa atrav´s da convolu¸˜o discreta y(kT ) = f (kT ) ∗ x(kT ). Esta
e e ca
parcela da resposta recebe o nome de resposta de Estado Zero.
yesz (kT ) = f (kT ) ∗ x(kT ).
3. A sa´ de um sistema depende das condi¸oes iniciais ci = y(iT ) (i = 0, . . . , n − 1).
ıda c˜
Esta parcela da resposta recebe o nome de resposta de Entrada Zero.
n−1
yenz (kT ) = fi (kT )ci
i=0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-152-320.jpg)
![6.7. Fun¸˜o de Transferˆncia Discreta e Estabilidade
ca e www.das.ufsc.br/labsil 153
4. A resposta de Entrada Zero ´ linear (afim) em rela¸ao `s condi¸˜es iniciais e a
e c˜ a co
resposta de Estado Zero ´ linear em rela¸˜o ` entrada.
e ca a
5. Os p´los de F (z) definem a estabilidade da resposta. Se F (z) possuir algum p´lo
o o
com m´dulo maior que a unidade ent˜o a resposta ter´ uma parcela que diverge. A
o a a
fun¸ao F (z) ´ conhecida como Fun¸˜o de Transferˆncia Discreta (ou pulsada) do
c˜ e ca e
sistema.
6.7.2 Resposta ao Pulso e Estabilidade
Quando as condi¸˜es iniciais s˜o nulas a sa´ de um sistema discreto linear invariante
co a ıda
s´ depende da entrada e da Fun¸ao de Transferˆncia Discreta, como pode ser visto em
o c˜ e
(6.14).
Dom´
ınio do Tempo: y(k) = f (k) ∗ x(k).
Dom´
ınio da Frequˆncia: Y (z) = F (z)X(z).
e
A fun¸ao f (k) = Z −1 [F (z)] recebe o nome de resposta ao pulso unit´rio pois f (k) ´ a
c˜ a e
resposta do sistema quando as condi¸˜es inciais s˜o nulas e a entrada ´ um pulso unit´rio
co a e a
no instante k = 0. (X(z) = 1).
Defini¸˜o 6.1 (Sistemas Causais ou N˜o-Antecipativos) Um sistema discreto ´ dito
ca a e
ser Causal (ou N˜o-Antecipativo) se a resposta de Estado Zero para um pulso unit´rio ´
a a e
nula para k < 0.
Num sistema causal o valor da resposta num dado instante de tempo y(kT ) n˜o depende
a
do sinal de entrada x(nT ) para valores de n > k. Caso contr´rio o valor da resposta no
a
instante t = kT passa a depender de valores futuros do sinal da entrada (x(t) para t > kT )
e que portanto ainda n˜o est˜o dispon´
a a ıveis no instante t = kT .
Mostraremos a seguir que um sistema ´ causal quando o polinˆmio do numerador da
e o
Fun¸ao de Transferˆncia F (z) possui grau ≤ ao do denominador.
c˜ e
Com (6.13) temos que:
an y(k + n) + · · · + a0 y(k) = bm x(k + m) + · · · + b0 x(k)
Observe que y(k + n) depende de x(k + m) e portanto se m > n a sa´ no instante
ıda
k + n depende de valores da entrada em instantes de tempo futuros pois k + m > k + n
para todo k. Logo para que um sistema discreto seja causal devemos ter m ≤ n.
Defini¸˜o 6.2 (Estabilidade) Um sistema discreto linear invariante no tempo ´ expo-
ca e
nencialmente est´vel se todos os p´los da sua Fun¸˜o de Transferˆncia Pulsada possuem
a o ca e
m´dulo inferior ` unidade. Caso contr´rio ´ dito ser inst´vel.
o a a e a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-153-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 154
Pela defini¸˜o acima, note que a estabilidade ´ uma propriedade intr´
ca e ınseca do sistema.
Ela s´ depende dos parˆmetros f´
o a ısicos do mesmo. N˜o depende da entrada nem das
a
condi¸˜es iniciais. O nome exponencialmente est´vel apenas enfatiza que os p´los da
co a o
Fun¸ao de Transferˆncia ser˜o a base de exponenciais no dom´
c˜ e a ınio do tempo e portanto
a resposta ao pulso converge exponencialmente para zero.
Exemplo 6.14 Verifique a estabilidade do sistema cuja fun¸˜o de transferˆncia ´
ca e e
z
F (z) =
(z − 1)(z + 2)
Solu¸˜o: Os p´los de F (z) s˜o z = 1 e z = −2 e pela defini¸˜o acima o sistema ´
ca o a ca e
inst´vel pois F (z) possui p´los fora do c´
a o ırculo unit´rio (ou sobre o c´
a ırculo). Para ver o
efeito desses p´los na resposta ao pulso unit´rio temos:
o a
1 z 1 z
F (z) = −
3z −1 3z +2
z
e como Z[ak ] = z−a
temos:
1 1
Z −1 = f (k) = (1)k − (−2)k
3 3
Assim, se algum p´lo da Fun¸˜o de Transferˆncia F (z) possuir m´dulo ≥ 1 a resposta
o ca e o
ao pulso n˜o tende ` zero. Ser´ crescente, oscilat´ria ou converge para um valor n˜o
a a a o a
nulo, caracterizando assim a instabilidade do sistema.
6.8 Sistemas Amostrados
Vimos que a transformada de Laplace ´ adequada ao tratamento de sinais e sistemas
e
de tempo cont´ ınuo. De forma an´loga a transformada Z nos possibilita o tratamento de
a
sinais e sistemas de tempo discreto. No entanto, a maioria dos sistemas a serem con-
trolados s˜o de natureza cont´
a ınua e s˜o controlados por computadores digitais (natureza
a
discreta). Essa mistura de sistemas cont´ınuos e discretos tornam o problema de an´lise
a
de estabilidade mais complicado pois tanto a transformada de Laplace como a trans-
formada Z j´ n˜o fornecem resultados satisfat´rios se aplicadas diretamente. A seguir
a a o
veremos como transformar sistemas amostrados em sistemas discretos equivalentes. Com
essa transforma¸˜o todos os sinais do sistema passam a ser discretos e a transformada Z
ca
pode ser usada sem maiores problemas na an´lise do sistema.
a
A figura 6.21(a) mostra um sistema cont´ ınuo G(s) cuja entrada x∗ (t) ´ um sinal
e
amostrado com amostrador ideal (trem de impulsos de per´ ıodo T ). A sa´ y(t) desse
ıda
sistema ser´ discretizada para posterior tramento num computador digital, isto ´ apenas
a e
os valores y(kT ) ser˜o considerados. Precisamos ent˜o saber qual seria o sistema discreto
a a
equivalente que tem as sequˆncias x(kT ) como entrada e y(kT ) como sa´
e ıda, como indica
a figura 6.21(b). O sistema discreto que procuramos possui as mesmas informa¸˜es do co
sistema amostrado e al´m disso a transformada Z pode ser aplicada diretamente.
e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-154-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 155
x(t) x∗ (t) y(t)|t=kT
G(s) (a)
T
x(kT ) y(kT )
G(z) (b)
Figura 6.21: Sistema amostrado e seu discreto equivalente
Note que a entrada do bloco anal´gico G(s) na figura 6.21(a) ´ um sinal amostrado
o e
onde os impulsos possuem ´reas de valores x(kT ) e a entrada do bloco discreto G(z) na
a
figura 6.21(b) ´ uma sequˆncia de valores x(kT ). A sa´ y(t) figura 6.21(a) ´ anal´gica
e e ıda e o
mas apenas os valores y(kT ) medidos nos instantes t = kT s˜o de interesse. J´ a sa´
a a ıda
na figura 6.21(b) ´ a pr´pria sequˆncia y(kT ).
e o e
A seguir apresentamos um procedimento para, dado o sistema anal´gico G(s), encontrar
o
o bloco discreto equivalente G(z). E equivalˆncia ` qual nos referimos ´ no sentido de
e a e
que os valores do sinal de entrada x(kT ) e sa´ y(kT ) do sistema discreto s˜o os mesmos
ıda a
do sistema cont´ınuo x(t), y(t) nos instantes t = kT .
Seja ent˜o g(t) = L−1 [G(s)] a resposta impulsional do sistema representado por G(s).
a
Da´ a resposta y(t) ´ dada pela convolu¸ao cont´
ı, e c˜ ınua da entrada com a resposta impul-
sional.
∞
ENTRADA: x∗ (t) = k=0 x(kT )δ(t − kT ), x(t) = 0 para t < 0.
SA´
IDA: y(t) = k
n=0 x(nT )δ(t − nT ) ∗ [g(t)], 0 ≤ t ≤ kT .
Sem perda de generalidade representamos y(t) no intervalo 0 ≤ t ≤ kT para algum
valor de k ≥ 0. Note que estamos supondo que G(s) representa um sistema causal e
portanto g(t) = 0 para t < 0.
Desenvolvendo a express˜o acima encontramos:
a
k
y(t) = x(nT )[δ(t − nT ) ∗ g(t)], 0 ≤ t ≤ kT
n=0
k
= x(nT ) g(t − nT )
n=0
Os valores de y(t) nos instantes t = kT s˜o dados por:
a
k
y(t)|t=kT = y(kT ) = x(nT )g(kT − nT ) (6.15)
n=0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-155-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 156
que ´ a convolu¸˜o discreta da sequˆncia de entrada x(kT ) com a sequˆncia de sa´
e ca e e ıda
y(kT ). Pela propriedade de convolu¸ao da Transformada Z temos tamb´m que:
c˜ e
Z[y(kT )] = Z[x(kT )]Z[g(kT )] ; Y (z) = X(z)G(z) (6.16)
As equa¸oes (6.15) e (6.16) definem a rela¸ao entre as sequˆncias x(kT ) e y(kT ) na
c˜ c˜ e
figura 6.21(b) que ´ o resultado desejado. Assim, para se obter o sistema discreto G(z)
e
equivalente a um sistema cont´ ınuo G(s), calcule g(t) = L−1 [G(s)] com a transformada
inversa de Laplace. Em seguida calcule a sequˆncia g(kT ) fazendo t = kT na fun¸ao g(t)
e c˜
obtida e finalmente calcule a fun¸˜o de transferˆncia do sistema discreto equivalente G(z)
ca e
aplicando a transformada Z na sequˆncia g(kT ) obtida. Um procedimento mais simples
e
para a passar de G(s) para G(z) est´ indicado na se¸˜o 6.4.4. A figura 6.22 mostra um
a ca
resumo dos principais resultados de convers˜o de Laplace para Z. .
a
α
Exemplo 6.15 Considere o sistema amostrado da figura 6.21(a) com G(s) = (s+a)(s+b) .
Calcule a fun¸˜o de transferˆncia discreta G(z) entre a sequˆncia x(kT ) de entrada e
ca e e
y(kT ) de sa´da indicada na figura 6.21(b).
ı
Solu¸˜o: Podemos resolver esse problema de duas formas:
ca
(1) Utilizando o Teorema do Res´duo apresentado na se¸˜o 6.4.4. Nesse caso temos
ı ca
G(z) = R(P1 ) + R(P2 )
z α z
R(P1 ) = (s + a)G(s) sT
=
z−e s=−a b − a z − e−aT
z α z
R(P2 ) = (s + b)G(s) =
z − esT s=−b a − b z − e−bT
α z z
⇒ G(z) = −aT
−
b−a z−e z − e−bT
que ´ a fun¸˜o de transferˆncia discreta desejada. Al´m disso, com a nota¸˜o Y (z) =
e ca e e ca
Z[y(kT )] e X(z) = Z[x(kT )] podemos escrever a rela¸˜o de entrada/sa´ do sistema
ca ıda
Y (z) = G(z)X(z).
(2) Utilizando as express˜es (6.15) e (6.16). Nesse caso temos
o
α 1 1 α
g(t) = L−1 [G(s)] = L−1 − = (e−at − e−bt )
b−a s+a s+b b−a
Discretizando a resposta impulsional g(t) obtemos:
α
g(t)|t=kT = g(kT ) = (e−akT − e−bkT )
b−a
tomando a Transformada Z da sequˆncia g(kT ) obtemos:
e
α z z
G(z) = Z[g(kT )] = −aT
−
b−a z−e z − e−bT](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-156-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 157
X(s) X ∗ (s) Y (s) Y ∗ (s)
G(s)
Y (z) = Z[Y ∗ (s)] = Z[G(s)X ∗ (s)]
= Z[G(s)]Z[X ∗ (s)]
= Z[G(s)] X(z)
X(s) Y (s) Y ∗ (s)
G(s)
Y (z) = Z[Y ∗ (s)] = Z[G(s)X(s)]
X1 (s)
Y (s) Y ∗ (s)
X2 (s)
ou de forma equivalente
∗
X1 (s) X1 (s)
Y ∗ (s)
X2 (s) ∗
X2 (s)
Y ∗ (s) = X1 (s) + X2 (s)
∗ ∗
Y (z) = Z[Y ∗ (s)] = Z[X1 (s)] + Z[X2 (s)]
∗ ∗
Y (z) = X1 (z) + X2 (z)
Figura 6.22: Resumo dos resultados de convers˜o de Laplace para Z
a](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-157-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 158
e finalmente temos:
Y (z) = G(z)X(z) Frequˆncia
e
y(kT ) = g(kT ) ∗ x(kT ) Tempo
A maioria dos sistemas amostrados possuem algum dispositivo sample-and-hold no seu
interior. A figura 6.23 mostra um sistema desse tipo. A fun¸ao ZOH(s) ´ a fun¸ao de
c˜ e c˜
transferˆncia do segurador de ordem zero como indicado em (6.4).
e
x(kT ) x∗ (t) y(t)|t=kT
ZOH(s) G(s)
T
Amostrador Segurador Sistema
de Ordem a ser
Ideal Controlado
Zero
Conversor D/A com S/H
Figura 6.23: Sistema amostrado com conversor D/A e S/H
Da figura 6.23 vamos definir a fun¸˜o auxiliar H(s) = ZOH(s)G(s). O problema agora
ca
´ encontrar a fun¸ao de transferˆncia discreta H(z) que corresponde ` fun¸ao H(s). Para
e c˜ e a c˜
sT
isso vamos utilizar a nota¸˜o H(z) = Z[H(s)]. Lembrando que e = z temos com (6.4)
ca
1 − e−T s G(s)
H(z) = Z[ZOH(s)G(s)] = Z[ G(s)] = (1 − z −1 )Z (6.17)
s s
1
Exemplo 6.16 Considere o sistema da figura 6.23 onde G(s) = s(s+1) . Calcule a fun¸˜o
ca
de transferˆncia Pulsada entre a sequˆncia x(kT ) e a sa´ y(t) nos instantes t = kT
e e ıda
com T = 1seg.
Solu¸˜o: Pelo resultado acima temos:
ca
1 − e−T s 1 1
H(z) = Z = (1 − z −1 )Z 2
s s(s + 1) s (s + 1)
1
Definindo F (s) = s2 (s+1)
podemos calcular F (z) atrav´s do teorema dos res´
e ıduos.
F (z) = R(P1 ) + R(P2 )
onde:
z z
R(P1 ) = (s + 1)F (s) =
z − eT s s=−1 z − e−1](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-158-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 159
e
d z
R(P2 ) = s2 F (s)
ds z − esT s=0
d 1 z
=
dss + 1 z − esT s=0
−1 z 1 −z
= 2 z − esT
+ (−T esT )
(s + 1) s + 1 (z − es T )2 s=0
z Tz
= − +
z − 1 (z − 1)2
Logo:
z z z
F (z) = −1
+ 2
−
z−e (z − 1) z−1
e portanto:
z−1 1
H(z) = (1 − z −1 )F (z) = −1
+ −1
z−e z−1
que ´ a fun¸ao de transferˆncia desejada.
e c˜ e
Exemplo 6.17 Considere o circuito RC do exemplo 6.2 onde o sinal de entrada ´ con-
e
stante por trechos. Represente o sinal constante por trechos como sendo a sa´ de um
ıda
segurador de ordem zero como indicado na figura 6.24. Calcule a equa¸˜o recursiva que
ca
rege o comportamento do sistema nos instantes t = kT . Calcule tamb´m a resposta do
e
circuito para um degrau unit´rio.
a
e(kT ) e∗ (t) y(t)|t=kT
ZOH(s) e(t) G(s)
T
Amostrador Segurador Circuito RC
de Ordem
Ideal
Zero
Figura 6.24: Circuito com entrada constante por trechos
Solu¸˜o: A fun¸˜o de transferˆncia Pulsada entre a sequˆncia de tens˜o de entrada
ca ca e e a
e(kT ) e a de sa´da y(kT ) pode ser obtida com:
ı
1 − e−T s 1 1
H(z) = Z = (1 − z −1 )Z
s RCs + 1 s(RCs + 1)
F (s)
−1 −1
= (1 − z )Z[F (s)] = (1 − z )[R(P1 ) + R(P2 )]
z z
R(P1 ) = sF (s) z−esT s=0
= z−1
z −z
R(P2 ) = (s + 1/RC)F (s) z−esT s=−1/RC
= z−e−T /RC](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-159-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 160
z z 1 − e−T /RC
⇒ H(z) = (1 − z −1 ) − =
z − 1 z − e−T /RC z − e−T /RC
Como Y (z) = H(z)E(z) temos a = e−T /RC e b = 1 − e−T /RC
Y (z)z − aY (z) = bE(z)
e pela propriedade de deslocamento obtemos:
y(kT + T ) − ay(kT ) = be(kT )
que ´ a equa¸ao recursiva desejada.
e c˜
z
Para calcular a resposta ao degrau unit´rio temos E(z) =
a z−1
e portanto Y (z) =
z
H(z) z−1 e por fra¸˜es parciais obtemos a resposta ao degrau:
co
z b
y(kT ) = Z −1 [Y (z)] = Z −1 [ ]
z −1z −a
= 1 − e−kT /RC , k = 0, 1, 2, . . .
Exemplo 6.18 Calcule a fun¸˜o de transferˆncia discreta dos sistemas indicados na
ca e
figura 6.25.
x(t) x∗ (t) 1 y1 (t) ∗
y1 (t) 1 y2 (t)|t=kT
s+a s+b (a)
T T
x(t) x∗ (t) 1 1 y(t)|t=kT (b)
s+a s+b
T
Figura 6.25: (a) Dois sistemas amostrados em cascata; (b) Dois sistemas cont´
ınuos em
cascata
Solu¸˜o: No caso da figura 6.25(a), a rela¸˜o entre as sequˆncias de entrada x(kT ) e
ca ca e
a de sa´da y1 (kT ) ´:
ı e
1 1
Z[y1 (kT )] = Z[ ] Z[x(kT )] ⇔ Y1 (z) = Z[ ] X(z)
s+a s+a
A rela¸˜o entre as sequˆncias de entrada y1 (kT ) e a de sa´ y2 (kT ) ´:
ca e ıda e
1 1
Z[y2 (kT )] = Z[ ] Z[y1 (kT )] ⇔ Y2 (z) = Z[ ] Y1 (z)
s+b s+b](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-160-320.jpg)
![6.8. Sistemas Amostrados www.das.ufsc.br/labsil 161
Combinando as duas express˜es acima temos que a fun¸˜o de transferˆncia Pulsada
o ca e
entre as sequˆncias x(kT ) e y2 (kT ) ´:
e e
1 1
Y2 (z) = Z[ ] Z[ ] X(z)
s+a s+b
1 z 1 z
Note que Z[ s+a ] = z−e−aT
e Z[ s+b ] = z−e−bT
.
No caso da figura 6.25(b), a rela¸˜o entre as sequˆncias de entrada x(kT ) e a de sa´
ca e ıda
y(kT ) ´:
e
1
Y (z) = Z X(z)
(s + a)(s + b)
Assim conclu´mos que
ı
1 1 z z
Z = −aT
−
(s + a)(s + b) b−a z−e z − e−bT
e portanto
1 1 1
Z Z =Z
(s + a) (s + b) (s + a)(s + b)
ou seja, os sistemas amostrados das figuras 6.25(a) e (b) s˜o diferentes pois suas respec-
a
tivas fun¸˜es de transferˆncia s˜o diferentes. Este resultado pode ser generalizado. Em
co e a
geral, para quaisquer fun¸˜es G1 (s) e G2 (s)
co
Z[G1 (s) G2 (s)] = Z[G1 (s)] Z[G2 (s)]
Exemplo 6.19 Prove o resultado da equa¸˜o (6.17).
ca
Solu¸˜o: Definindo H(s) como sendo a transferˆncia da sequˆncia x(kT ) para a sa´
ca e e ıda
y(t) temos:
1 − e−T s G(s) G(s)
H(s) = G(s) = − e−T s
s s s
G(s)
Definindo h0 (t) = L−1 s
e lembrando que L−1 [e−T s G(s)/s] = h0 (t − T ) a resposta
−1
impulsional ´: h(t) = L [H(s)] = h0 (t) − h0 (t − T )
e
Os valores de h(t) nos instantes t = kT formam a seguinte sequˆncia (resposta ao pulso
e
unit´rio).
a
h(kT ) = h0 (kT ) − h0 (kT − T )
Tomando a Transformada Z de h(kT ) vem
H(z) = Z[h(kT )] = Z[h0 (kT )] − Z[h0 (kT − T )]
Note que G(s) ´ um sistema f´sico e portanto causal. Logo G(s)/s tamb´m ´ causal e
e ı e e
portanto h0 (t) = 0 para t < 0. Assim:
∞
Z[h0 (kT − T )] = h0 (kT − T )z −k = h0 (−T ) + h0 (0)z −1 + h0 (T )z −2 + . . .
k=0](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-161-320.jpg)
![6.9. Sistemas Realimentados www.das.ufsc.br/labsil 162
como h0 (−T ) = 0 temos:
Z[h0 (kT − T )] = z −1 [h0 (0) + h0 (T )z −1 + h0 (2T )z −2 + . . .
∞
−1
= z [ h0 (kT )z −k ] = z −1 Z[h0 (kT )]
k=0
e portanto obtemos o seguinte resultado:
1 − e−T s
para H(s) = G(s)
s
G(s)
temos H(z) = (1 − z −1 )Z[h0 (kT )] = (1 − z −1 )Z[ ]
s
logo:
Z[x(kT )] = H(z) Z[y(kT )]
X(z) Y (z)
que ´ o resultado desejado.
e
6.9 Sistemas Realimentados
A id´ia de sistemas discretos realimentados ´ an´loga a de sistemas realimentados
e e a
cont´ınuos. Uma estrutura comum de controle de sistemas amostrados est´ indicada na
a
figura 6.26(a). A figura 6.26(b) mostra uma reinterpreta¸˜o do sistema em (a) enfatizando
ca
as fun¸˜es executadas pelo computador e medidor digital. A figura 6.26(c) mostra o
co
sistema discreto correspondente aos casos (a),(b). Nos instantes t = kT o modelo discreto
possui as mesmas entradas e sa´ ıdas do sistema cont´ ınuo indicado nos casos (a) e (b) e
al´m disso possui a vantagem de poder ser tratado diretamente pela transformada Z. O
e
modelo discreto depende, entre outros fatores, da localiza¸˜o dos conversores A/D e D/A.
ca
Para verificar essa afirma¸ao considere os sistemas da figura 6.27 e suponha que estamos
c˜
interessados nas fun¸oes de transferˆncia Pulsadas entre as sequˆncias r(kT ) e c(kT ) nos
c˜ e e
casos (a) e (b).
Vamos primeiro considerar o sistema da figura 6.27(a). Para encontrar a fun¸ao de
c˜
transferˆncia entre as sequˆncias e(kT ) e c(kT ) temos
e e
C(z) = G(z)E(z) onde G(z) = Z[ZOH(s)G(s)]
e a fun¸˜o de transferˆncia entre e(kT ) e v(kT ) ´:
ca e e
V (z) = GH(z)E(z) onde GH(z) = Z[ZOH(s)G(s)H(s)]
Como E(z) = R(z) − V (z) temos:
C(z)
R(z) = E(z) + GH(z)E(z) = (1 + GH(z))
G(z)](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-162-320.jpg)
![6.9. Sistemas Realimentados www.das.ufsc.br/labsil 163
modelo do modelo do modelo do modelo do
conversor programa do conversor D/A sistema a ser
controlado vari´vel
a
A/D com S/H
sinal de computador controlada
referˆncia +
e e(t) e(kT ) u(kT )
ZOH(s)
u(t)
G2 (s) y(t)
G1 (z)
r(t) -
(a)
modelo do modelo do modelo do
computador conversor D/A sistema a ser medidor com
com S/H controlado conversor A/D
algor´
ıtmo
sinal de (eq. recursiva)
referˆncia +
e u(kT )
ZOH(s)
u(t)
G2 (s) y(kT )
G1 (z)
r(kT ) e(kT ) vari´vel
a
-
controlada
(b)
modelo discreto do conjunto
conversor D/A, sistema,
medidor e conversor A/D
algor´
ıtmo vari´vel
a
G3 (z) = Z[ZOH(s) G2 (s)]
sinal de (eq. recursiva) controlada
referˆncia +
e e(kT ) u(kT )
G3 (z) y(kT )
G1 (z)
r(kT ) -
(c)
Figura 6.26: Sistema de controle digital e seu modelo discreto](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-163-320.jpg)
![6.9. Sistemas Realimentados www.das.ufsc.br/labsil 164
sistema, controlador e
S/H medidor anal´gico
o
referˆncia
e
e(t) c∗ (t)
r(t) e∗ (t) G(s) (a)
+ ZOH(s)
- T T vari´vel controlada
a
v(t) H(s)
filtros auxiliares
sistema, controlador e
medidor digital S/H
referˆncia
e S/H
r(t) e(t) e∗ (t) (b)
ZOH(s) G(s) c∗ (t)
+
- T T vari´vel controlada
a
v(t)
H(s) ZOH(s)
filtros auxiliares
Figura 6.27: Sistema de controle digital com medidor anal´gico (a) e digital (b)
o
e portanto:
G(z)
C(z) = R(z)
1 + GH(z)
que expressa a rela¸˜o entre a sequˆncia r(kT ) e c(kT ) no sistema da figura 6.27(a).
ca e
Passemos agora ao sistema da figura 6.27(b). Para encontrar a fun¸˜o de transferˆncia
ca e
entre as sequˆncias e(kT ) e c(kT ) temos
e
C(z) = G(z)E(z) onde G(z) = Z[ZOH(s)G(s)]
e a fun¸˜o de transferˆncia entre c(kT ) e v(kT ) ´:
ca e e
V (z) = H(z)C(z) onde H(z) = Z[ZOH(s)H(s)]
Como E(z) = R(z) − V (z) temos:
C(z) C(z)
R(z) = + H(z)C(z) = (1 + G(z)H(z))
G(z) G(z)
e portanto:
G(z)
C(z) = R(z)
1 + G(z)H(z)
que expressa a rela¸˜o entre a sequˆncia r(kT ) e c(kT ) no sistema da figura 6.27(b).
ca e](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-164-320.jpg)
![6.10. Escolha do Per´
ıodo de Amostragem www.das.ufsc.br/labsil 165
r(t) e(t) e∗ (t) Va (t) c∗ (t)
ZOH(s) 1
+ s(s+1)
- T=1seg T=1seg
Va (t) Tens˜o de armadura do motor DC
a
c(t) Posi¸˜o angular da carga acionada
ca
r(t) Sinal de referˆncia
e
Figura 6.28: Controle digital de posi¸˜o angular atrav´s de um motor DC
ca e
Exemplo 6.20 Obtenha a resposta ao degrau unit´rio c(kT ) para o sistema de controle
a
de posi¸˜o acionado por um Motor DC, como indicado na figura 6.28.
ca
Solu¸˜o: De um exemplo anterior j´ vimos que:
ca a
e−1 z + 1 − 2e−1 0, 368z + 0, 264
G(z) = Z[G(s)] = = 2
z 2 − (1 + e−1 )z + e−1 z − 1, 368z + 0, 368
Logo:
C(z) 0, 368z + 0, 264
= 2
R(z) z − z + 0, 632
z
Para uma entrada degrau unit´rio R(z) =
a z−1
temos:
0, 368z + 0, 264 z
C(z) =
z 2 − z + 0, 632 z − 1
Por divis˜o polinomial obt´m-se:
a e
C(z) = 0, 368z −1 + z −2 + 1, 4z −3 + 1, 4z −4 + 1, 147z −5 + 0, 895z −6 + 0, 802z −7 + . . .
Problema 6.4 Com o aux´lio de uma tabela de transformadas e da transformada inversa
ı
encontre a express˜o anal´tica para c(kT ) no exemplo 6.20.
a ı
´
Problema 6.5 E importante notar que o m´todo da Transformada Z fornece os valores
e
da sa´ c(t) apenas nos instantes de amostragem t = kT . O valor de c(t) entre instantes
ıda
de amostragens consecutivos n˜o pode ser obtido pela Transformada Z . Com o aux´ de
a ılio
um programa de simula¸˜o verifique que os resultados anal´
ca ıticos obtidos coincidem com
o resultado da simula¸˜o do sistema de controle indicado no exemplo 6.20.
ca
6.10 Escolha do Per´
ıodo de Amostragem
A melhor escolha do per´
ıodo de amostragem em sistemas de controle ´ um compromisso
e
entre v´rios fatores normalmente contradit´rios. Normalmente a performance de um
a o](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-165-320.jpg)
![6.11. Resposta em Frequˆncia
e www.das.ufsc.br/labsil 166
controlador digital melhora com o aumento da frequˆncia de amostragem mas o custo
e
do dispositivo tamb´m. Diminui¸˜o da frequˆncia de amostragem significa mais tempo
e ca e
dispon´ para o c´lculo do sinal de controle em tempo real, o que possibilita a utiliza¸ao
ıvel a c˜
de computadores mais lentos e portanto mais baratos. Para sistemas com conversores
A/D, menor frequˆncia de amostragem significa que menor velocidade de convers˜o ´
e a e
necess´ria, o que tamb´m diminui o custo do dispositivo. Al´m disso, normalmente uma
a e e
grande frequˆncia de amostragem requer uma grande precis˜o na representa¸˜o bin´ria
e a ca a
(n´mero de bits elevado), o que tamb´m aumenta o custo.
u e
V´rios fatores afetam a performance de controladores digitais e para que o sistema apre-
a
sente uma performance m´ ınima aceit´vel se faz necess´rio uma frequˆncia de amostragem
a a e
m´ınima muito superior `quela fornecida pelo Teorema da Amostragem.
a
Para o sistema de controle digital da figura 6.26 vamos definir ωb a frequˆncia de banda
e
passante desejada do sistema em malha fechada e ωa = 2π a frequˆncia de amostragem
T
e
que precisamos utilizar para que a performance do sistema n˜o se deteriore demais em
a
rela¸˜o ` do sistema desejado. A banda passante desejada do sistema deve ser escolhida
ca a
em fun¸ao dos requisitos de rapidez de resposta desejados em malha fechada. Ent˜o os
c˜ a
seguintes fatores imp˜em um limite m´
o ınimo para que ωa que em muitas aplica¸˜es ´ dado
co e
por ωa > 20ωb .
1. Seguir sinais de referˆncia com energia dentro da banda passante do sistema.
e
2. Tempo de acomoda¸ao pequeno e pouca oscila¸ao.
c˜ c˜
3. Erros devido ` perturba¸oes e ru´
a c˜ ıdos que incidem sobre o sistema a ser controlado
dificultando o controle adequado.
4. Degrada¸ao da estabilidade que aumenta com a diminui¸ao da frequˆncia de amostragem
c˜ c˜ e
devido ` sensibilidade ` erros nos parˆmetros do modelo. Isto ´ acentuado ainda
a a a e
mais em conversores com palavra de tamanho pequeno.
5. Introdu¸ao de prefiltros (anal´gicos) de amostragem para atenuar ru´
c˜ o ıdos de medida
mas que tamb´m podem introduzir defasagens na vari´vel medida dificultando o
e a
projeto do controlador em alguns casos.
Para maiores detalhes veja por exemplo [9],[2].
6.11 Resposta em Frequˆncia
e
Como vimos anteriormente a Transformada Z de um sinal amostrado pode ser definida
a partir da Transformada de Laplace do sinal amostrado com a mudan¸a de vari´vel
c a
Ts
z = e . Esta rela¸ao mostra como os p´los do plano s de Laplace s˜o mapeados para o
c˜ o a
plano z.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-166-320.jpg)
![6.11. Resposta em Frequˆncia
e www.das.ufsc.br/labsil 167
Exemplo 6.21 O sinal y(t) = e−at cos(bt), t ≥ 0 com aT = 0, 3567 e bT = π/4 resulta
na seguinte sequˆncia para T = 1seg.
e
y(kT ) = (e−3567 )k cos(πk/4), k = 0, 1, 2, . . .
= 0, 7k cos(πk/4)
Calcule a rela¸ao entre os p´los de Y (s) e Y (z).
c˜ o
Solu¸˜o: Com o aux´lio das transformadas de Laplace e Z podemos montar a seguinte
ca ı
tabela:
P´los de Y (s) P´los de Y (z)
o o
s1 = −a − jb z1 = e−aT e−jbT = es1 T
s2 = −a + jb z2 = e−aT ejbT = es2 T
Pelo exemplo acima confirmamos que se uma transformada Y (s) possui todos os p´los o
no semiplano negativo (est´vel) ent˜o Y (z) ter´ todos os p´los dentro do c´
a a a o ırculo unit´rio
a
(est´vel). Se algum p´lo de Y (s) est´ sobre o eixo imagin´rio ele ser´ mapeado em Y (z)
a o a a a
sobre o c´
ırculo unit´rio e finalmente um p´lo de Y (s) no semiplano direito (inst´vel) ser´
a o a a
mapeado em Y (z) na regi˜o fora do c´
a ırculo unit´rio (inst´vel). Veja figuras 6.15-6.17.
a a
Vimos tamb´m que a resposta senoidal em regime permanente de um sistema linear
e
invariante em Laplace ´ completamente determinada pela Fun¸˜o de Transferˆncia do
e ca e
sistema com s = jω0 , como indicado nas figuras 4.2 e 4.3. Em outras palavras, a reposta
frequencial de um sistema cont´
ınuo se obt´m fazendo s percorrer todo o eixo imagin´rio
e a
(s = jω). Como todos os pontos sobre o eixo imagin´rio s˜o mapeados sobre o c´
a a ırculo
unit´rio da Transformada Z podemos conclu´
a ımos que a resposta frequencial de um sis-
e ırculo unit´rio, isto ´, z = ejωT .
tema discreto se obt´m fazendo z percorrer todo o c´ a e
A seguir mostraremos que resultados an´logos aos das figuras 4.2 e 4.3 s˜o v´lidos para
a a a
sistemas discretos.
Seja o sitema discreto abaixo:
X(z) Y(z)
F(z)
Figura 6.29: Sistema discreto est´vel
a
onde F (z) ´ est´vel e a entrada ´ uma sequˆncia senoidal x(k) = cos(ω0 kT ), k ≥
e a e e
0. A resposta em regime tamb´m ser´ uma cossen´ide de mesma frequˆncia por´m
e a o e e
com amplitude e fase que dependem de F (z) para z = ejω0 T . Para mostrar isso vamos
representar F (ejω0 T ) em termos de sua coordenada polar:
|F (ejω0 T )| = M
⇒ F (ejω0 T ) = M ejφ
∠F (ejω0 T ) = φ
1 z z
Como X(z) = Z[x(k)] = 2 z−ejω0 T
+ z−e−jω0 T
temos:](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-167-320.jpg)

![6.12. Problemas Complementares www.das.ufsc.br/labsil 169
R = 3Ω L = 1H
+ +
v(t) C = 1F vc (t)
- -
Figura 6.31: Circuito RLC com entrada constante por trechos
e portanto a dinˆmica da velocidade do motor em fun¸˜o da tens˜o de armadura pode
a ca a
ser representada pela equa¸˜o diferencial w(t) + 2w(t) = va (t). Pede-se: (i) a fun¸˜o
ca ˙ ca
de transferˆncia discreta de malha fechada; (ii) verifique se o sistema ´ est´vel e justi-
e e a
fique sua resposta; (iii) a velocidade de regime permanente do motor quando o sinal de
referˆncia ´ um degrau unit´rio.
e e a
r(t)
e(kT) u(kT) va (t) w(t)
computador S/H motor
+
- T
Figura 6.32: Sistema de controle de velocidade
Problema 6.8 A resposta de um sistema linear invariante ao degrau de amplitude dois
e certas condi¸˜es iniciais ´ y1 (k) = 2 + 1, 4616(0, 0729)k − 2, 4616(0, 682)k onde k ≥ 0.
co e
Para um degrau unit´rio e o dobro das condi¸˜es iniciais a resposta ´ y2 (k) = 1 +
a co e
k k
2, 4102(0, 0729) − 1, 4102(0, 682) . Pede-se (no dom´ ınio do tempo):
(i) A equa¸˜o recursiva do sistema.
ca
(ii) A resposta ao pulso unit´rio.
a
(iii) A resposta de estado zero na situa¸˜o 1.
ca
(iv) A resposta de entrada zero na situa¸˜o 1.
ca
(v) As condi¸˜es iniciais da situa¸˜o 1.
co ca
Problema 6.9 Verifique se os sistemas da figura 6.33 s˜o est´veis. Justifique sua re-
a a
sposta.
Problema 6.10 Seja x(k) uma sequˆncia onde x(k) = 0, ∀k < 0. Mostre que :
e
(a) Z[x(k + 1)] = Z[x(k)]z − x(0)z
(b) Z[x(k − 1)] = Z[x(k)]z −1](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-169-320.jpg)

![Bibliografia
[1] K. OGATA, Engenharia de Controle Moderno, Prentice Hall 1993.
[2] K. OGATA, Discrete Time Control Systems, Prentice Hall, 1995.
[3] C.T. CHEN, System and Signal Analysis, Saunders 1989.
[4] A.V. OPPENHEIM, A.S. WILLSKY,Signal and Systems, Prentice Hall 1983.
[5] B.P. LATHI, Sistemas de Comunica¸˜o, Editora Guanabara, 1987.
ca
[6] J.J. d’ Azzo, C.H.Houpis, An´lise e projeto de sistemas de controle lineares, Editora
a
Guanabara 1988.
[7] K.A.STROUD, Engineering mathematics, MacMillan Press, 1995.
[8] R.T.STEFANI, C.L.SAVANT, B.SHAHIAN, G.H.HOSTETTER, Design of feedback
control systems, Saunders College Publishing, 1994.
[9] G.F.Franklin, J.D.Powell, M.L.Workman, Digital control of Dinamic Systems,
Addison-Wesley, 1990.](https://image.slidesharecdn.com/apostila-lineares-pdf-110315143906-phpapp01/85/Apostila-lineares-pdf-171-320.jpg)