Este documento apresenta uma análise estrutural de estruturas reticuladas. Discute a representação matemática de estruturas, as relações de elasticidade, a indeterminação estática e cinemática, e os métodos de análise de forças e deslocamentos. Apresenta aplicações destes métodos a diferentes elementos estruturais como vigas, porticos e grelhas.

































































































































































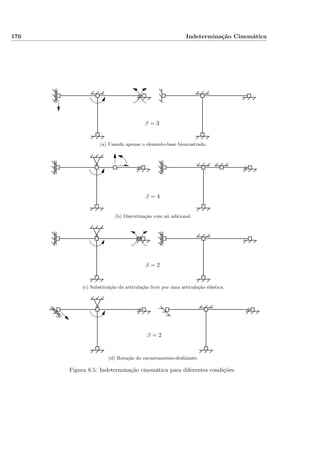






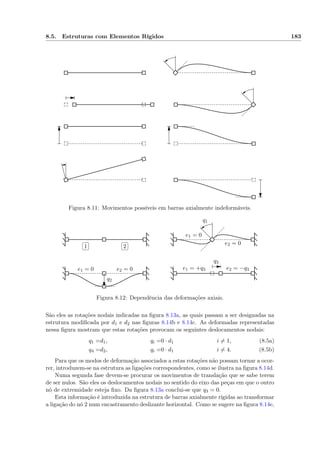

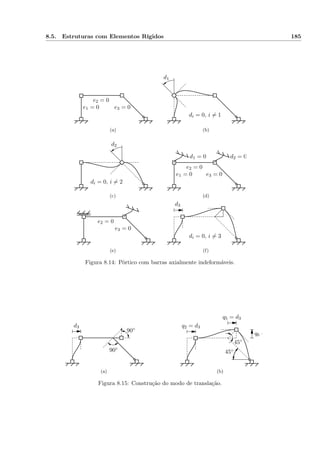


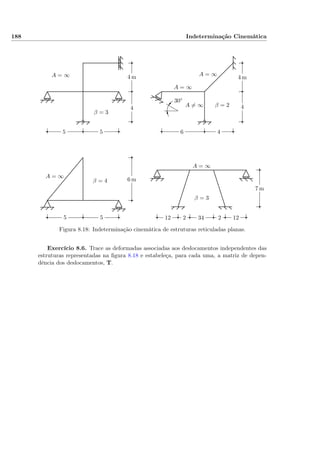






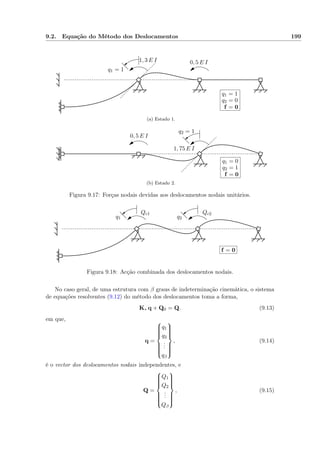

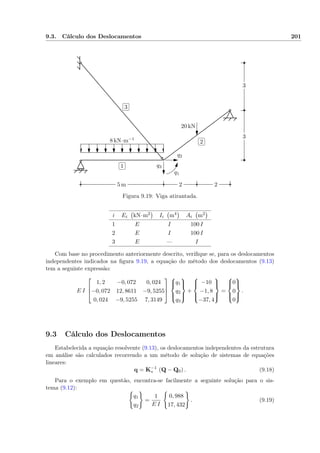



















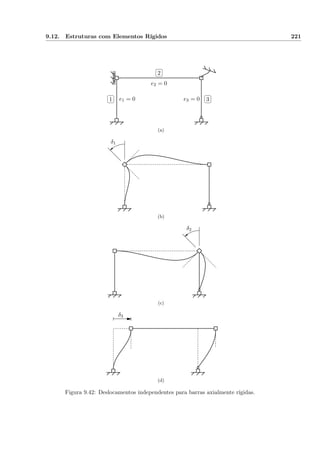


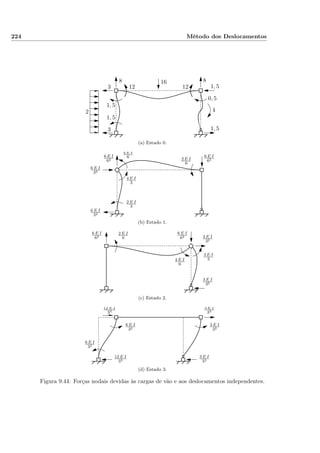











![9.17. Barras com Troços Rígidos 237
Por exemplo, e de acordo com a definição (9.55a), para as condições de indeformabili-
dade axial e de indeformabilidade à flexão,
ur = e = 0
ur =
θi = 0
θj = 0
obtêm-se as seguintes definições para a matriz de compatibilidade associada aos modos
rígidos, respectivamente:
ArN = 0 −1 0 0 +1 0
ArN =
−1 0 −1/L 0 0 +1/L
0 0 +1/L +1 0 −1/L
O comportamento de barras rígidas é simulado combinando estas duas condições, mos-
trando a condição de compatibilidade (9.61) que, no caso plano, apenas 3 dos 6 desloca-
mentos nodais permanecem independentes (ou 6 em 12, no caso tridimensional).
A equação fundamental do método dos deslocamentos continua a ser obtida combi-
nando as condições de compatibilidade (9.61)) e de equilíbrio (9.62) com as relações de
elasticidade, sendo os esforços associados aos modos indeformáveis agora tratados como
variáveis independentes:
KNN AT
rN
ArN O
qN
Xr
=
QN − QN0
ur
(9.63)
Exercício 9.25. Generalize a equação dos trabalhos virtuais e a definição da energia
potencial para incluir o efeito de modos indeformáveis e de deformações independentes
impostas.
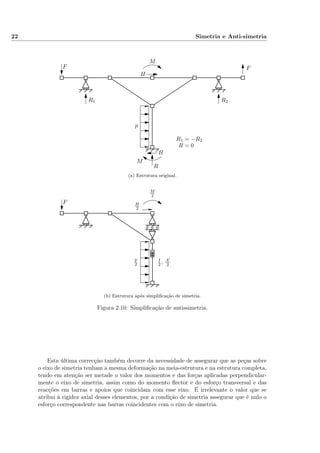
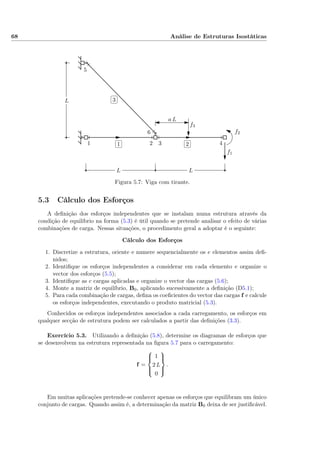
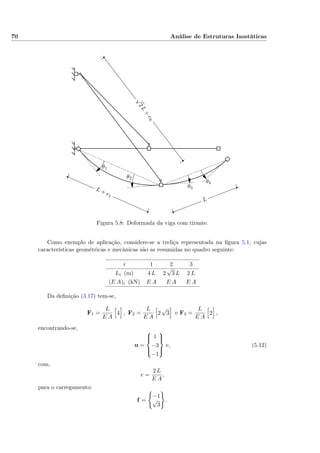
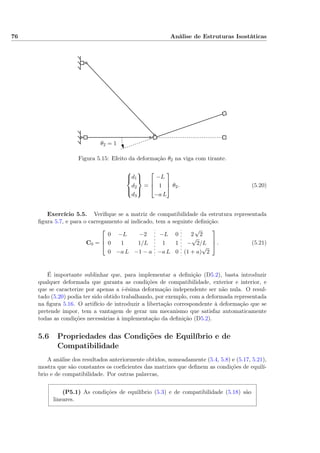
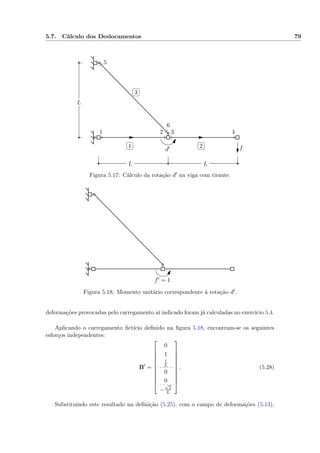
9.17 Barras com Troços Rígidos
Os resultados anteriormente obtidos permanecem válidos para barras com troços rí-
gidos, sendo no entanto necessário actualizar as definições (9.55) das matrizes de com-
patibilidade para incluir o efeito das excentricidades em relação ao referencial da peça
deformável. Deixa-se para exercício verificar, por compatibilidade e por equilíbrio, que são
os seguintes os resultados que se obtêm para a geometria indicada na figura (9.58), quando
os deslocamentos e as forças são medidos no referencial do troço deformável da barra:
AuN =
− (1 + ρ1) 0 −1/L −ρ2 0 +1/L
ρ1 0 +1/L 1 + ρ2 0 −1/L
[ρ1 (ρ4 − ρ3) + ρ3] L −1 ρ4 − ρ3 [ρ2 (ρ4 − ρ3) − ρ4] L +1 ρ3 − ρ4
(9.64a)
AδN =
−ρ1 0 −1/L −ρ2 0 +1/L
[ρ1 (ρ4 − ρ3) + ρ3] L +1 ρ4 − ρ3 ρ2 (ρ4 − ρ3) L 0 ρ3 − ρ4
(1 − η3) ρ2 L 0 1 − η3 −η3 ρ2 L 0 +η3
(9.64b)](https://image.slidesharecdn.com/aeer-140607192219-phpapp01/85/Analise-de-Estruturas-243-320.jpg)


