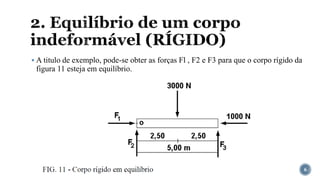
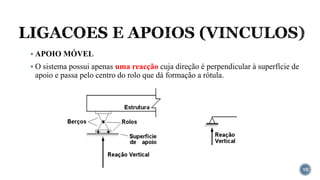
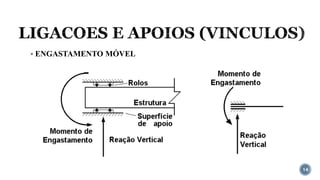
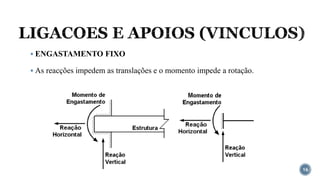
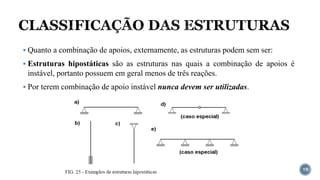
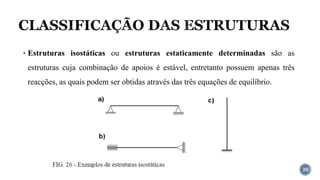
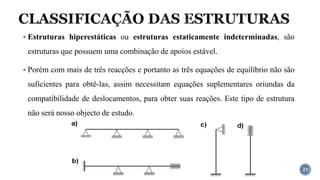
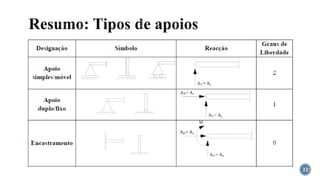
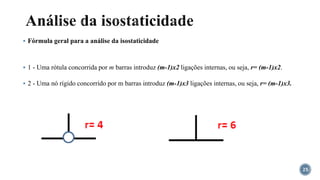
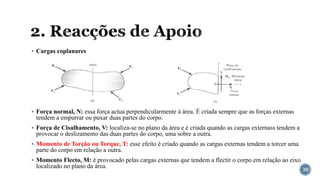
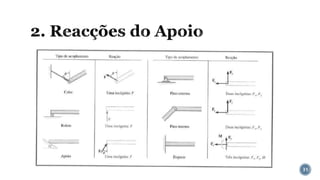
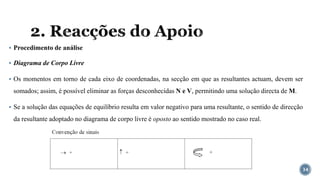
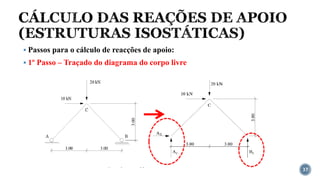
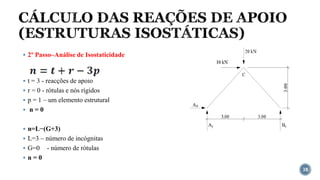
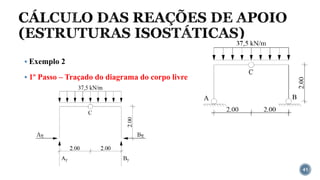
O documento aborda o equilíbrio de corpos rígidos, explicando como estruturas são analisadas em relação às forças e momentos aplicados. Ele discute diferentes tipos de apoios e suas características, categorizando estruturas em hipostáticas, isostáticas e hiperestáticas com base nas reações de apoio. A análise de isostaticidade e o cálculo de reações são apresentados como fundamentais para garantir a estabilidade das estruturas.