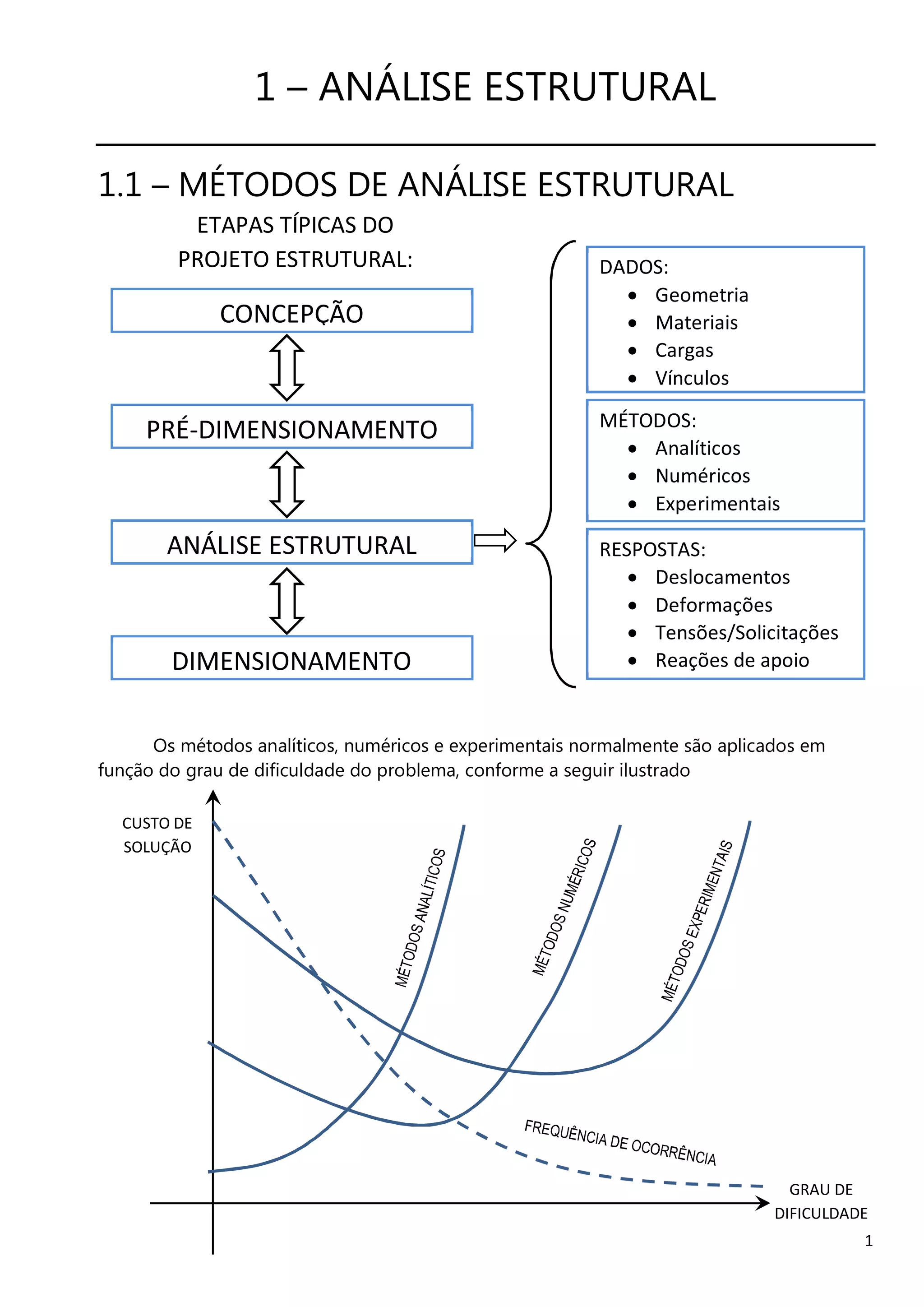
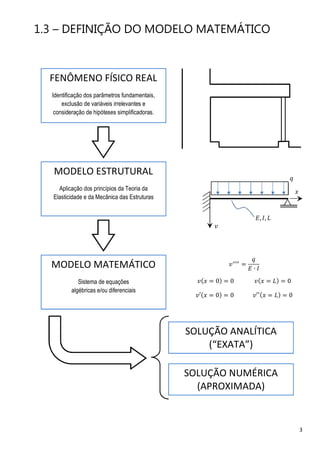
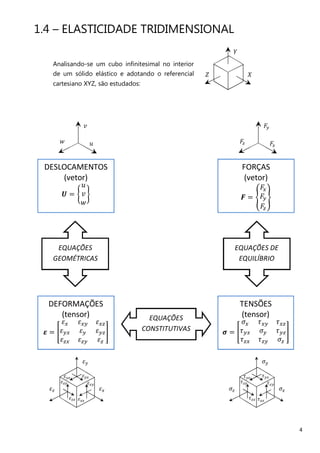
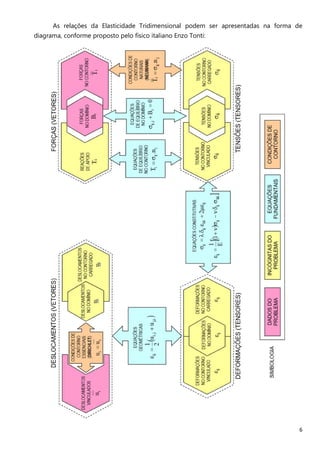
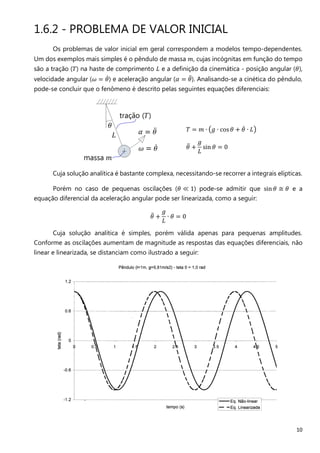
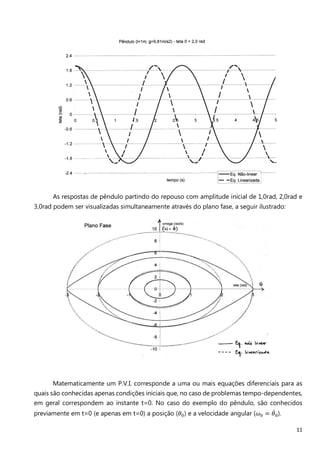
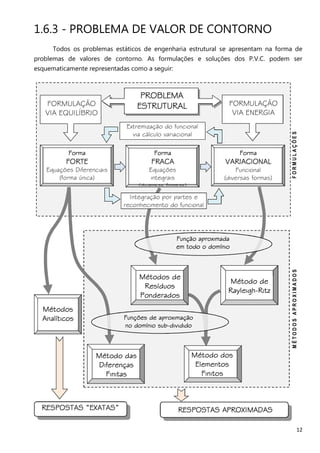
O documento descreve os principais métodos e conceitos de análise estrutural, incluindo a história do desenvolvimento da engenharia estrutural, a definição do modelo matemático, as equações da elasticidade tridimensional e os principais modelos matemáticos para análise de diferentes tipos de estruturas.