Este documento apresenta a lista de autoridades e coordenadores da Secretaria Municipal de Educação de Duque de Caxias no ano de 2013, com seus respectivos cargos e funções. Também contém os índices dos volumes I e II do Projeto (Con)Seguir, referentes às disciplinas de Matemática e Língua Portuguesa do 2o Segmento.


















![VOLUME I
MATEMÁTICA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 19 MATEMÁTICA - 2013
CAPÍTULO 4 – NÚMEROS INTEIROS
OPERAÇÕES E PROBLEMAS COM NÚMEROS INTEIROS:
Definição: Chama-se conjunto dos números inteiros - (Z) - o
seguinte conjunto
Z = {...,-3,-2,-1,0,1,2,3,...}
Canadá (– 8ºC) Rio de Janeiro (+40ºC)
Estes números podem ser representados numa reta
numérica:
Obs 1: O zero não é nem positivo nem negativo.
Como os números inteiros aumentam da esquerda para
direita, temos:
- 3 > - 4 ; - 2 < 1 e -5 < 0
Crédito: quantia que se tem a receber.
Débito: quantia que se deve.
O zero é a referência para o débito e o crédito.
Obs 2: Os números positivos indicam lucros, altitudes acima
do nível do mar, datas depois de cristo,créditos, ...
Os números negativos indicam situações opostas:
prejuízos, altitudes abaixo do nível do mar, datas antes de
cristo, débitos, ....
OPERAÇÕES EM Z:
ADIÇÃO DE NÚMEROS INTEIROS
→ Regras para ADIÇÃO de Inteiros
1) SINAIS IGUAIS >> SOMAR e REPITIR O SINAL
2) SINAIS DIFERENTES >> SUBTRAIR e REPETIR O
SINAL DO MAIOR.
Ex:
a) (+4) + (+5) = +9 b) (+4) + (–5) = –1
c) (–4) + (+5) = +1 d) (–4) + (–5) = –9
Propriedades da Adição em Z
[A1] - associativa da adição: (a + b) + c = a + (b + c)
[A2] - comutativa da adição: a + b = b + a
[A3] - elemento neutro da adição: a + 0 = a
[A4] - simétrico da adição: a + (-a) = 0
Obs
Devido a [A4], podemos definir em Z a operação de
subtração, estabelecendo que a - b = a + (-b) para todos a e
b Z.
Ex: O simétrico ou oposto de 7 é –7.
Ou seja: – (+7) = –7 ou –( –7) = + 7
SUBTRAÇÃO DE NÚMEROS INTEIROS
Subtrair números inteiros corresponde a adicionar o
oposto:
Ex: (+5) – (+6) = 5 – 6 = –1
(–5) – (+6) = –5 – 6 = –11
(–5) – (–6) = –5 + 6 = 1
(+5) – (–6) = 5 + 6 = 11](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-25-320.jpg)
![VOLUME I
MATEMÁTICA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 20 MATEMÁTICA - 2013
MULTIPLICAÇÃO DE NÚMEROS INTEIROS
Na multiplicação de dois números naturais, o primeiro
fator indica quantas vezes o segundo deve ser
adicionado. O resultado da adição é o produto dos dois.
A mesma interpretação aplica-se quando o primeiro
fator é um número natural e o segundo, um número
negativo:
3 x (-2) pode ser visto como o resultado da adição de
três parcelas iguais a (-2), isto é:
(-2) + (-2) + (-2), igual a -6.
Entretanto, que interpretação dar quando o primeiro
fator é negativo? Por analogia e coerência matemática,
podemos dizer que ele indica quantas vezes o segundo
deve ser subtraído, ou retirado.
Uma abordagem financeira
Agora pense um pouco: se valores negativos são
retirados ou desaparecem (por exemplo, no caso de
dívidas serem perdoadas) então sua situação
financeira melhora, certo?
Veja um exemplo simulado:
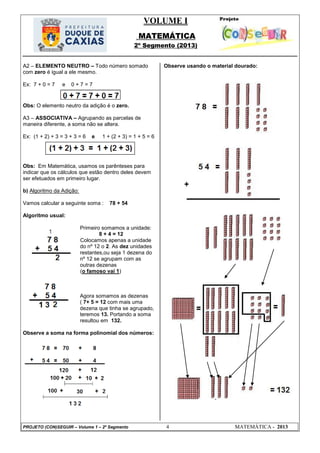
Saldos e parcelas a receber: 205,00 + 55,00 + 20,00 =
280,00
Dívidas: 40,00 + 60,00 + 60,00 + 60,00 + 60,00 =
280,00
No fundo, você está zerado. Tudo que você tem ou
receberá já está comprometido.
Veja a tabela:
Entretanto, suponha que uma liminar da Justiça
impediu a prefeitura de cobrar-lhe as quatro parcelas
de 60,00.
Como fica sua situação agora?
Será coincidência? Você estava sem nada e agora tem
R$240,00 para gastar, exatamente o valor de 4
parcelas de R$60,00.
Será que retirar quatro dívidas de R$60,00 corresponde
a somar R$240,00? Ou seja:
Será que (–4) x (–60,00) = 240,00?
A resposta é sim.
→ Regras para MULTIPLICAÇÃO de Inteiros
Ex:
a) (+5) . (+6) = + 30 a) (+5) . (–6) = – 30
a) (–5) . (+6) = – 30 a) (–5) . (–6) = + 30
Propriedades da Multiplicação de Inteiros
[M1]- associativa da multiplicação: (a.b).c = a .(b.c)
[M2] - comutativa da multiplicação: a . b = b . a
[M3]-elemento neutro da multiplicação: a . 1 = a
[D]- Distributiva: a . (b + c) = a .b + a . c
DIVISÃO DE NÚMEROS INTEIROS
A regra de sinais para dividir inteiros é a mesma da
multiplicação.
Ex:
a) (+ 30) : (+6) = + 5
d) (+ 30) : (–6) = – 5
d) (– 30) : (+6) = – 5
d) (– 30) : (–6) = + 5](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-26-320.jpg)
![VOLUME I
MATEMÁTICA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 21 MATEMÁTICA - 2013
EXERCÍCIOS DE FIXAÇÃO
62) Resolva as expressões abaixo:
A) 38 + 75 = F) 122 + 122 =
B) 38 75 = G) 43 62 + 17=
C) 5 38 = H) 43 62 + 17=
D) 64 19 = I) 43 62 + 17 + 76 =
E) 64 + 19 = J) 43 62 + 17 76 =
63) Resolva as expressões abaixo:
A) 10 + [ 8 + (15 11) 10 ] + 1 =
B) 15 [ 2 (3 5 + 1) 6 ] 1 =
64) Determine os produtos:
A) (+5).(+6) =
B) (5).(+6) =
C) (5).(6) =
D) (+3).(5).(+5) =
E) (+1).(+1).(1) =
F) (3).(4).(+6).(+2) =
G) (5).(5) =
H) (5).(2).(2) =
I) (+13).(3).(+4) =
J) (+1).(2).(0) =
65) Resolva as expressões abaixo:
A) 8 . { 5 [ 3 + 4 .(1 + 1) + 2 ] + 1 } + 8 =
B) 5 . [ 8 + 7 : (9 + 2) 1 ] + 1 =
66) Determine os produtos:
A) (+3).(+7) =
B) (3).(+7) =
C) (3).(7) =
D) (+2).(6).(+4) =
E) (+10).(+1).(1) =
F) (3).(2).(+5).(+4) =
67) Calcule as potências abaixo:
A) (1)
2
= b) (+6)
2
=
C) (2)
2
= d) (5)
2
=
E) (3)
3
= f) (+3)
3
=
68) Resolva as expressões numéricas abaixo:
A) (10).(2) + (6).(3) =
B) (20):(5) – (2).(3) =
C) (8):(2) – (18):(6) =
D) (20):(5) + (7).(3) =
E) (36):(6) – (30):(3) =
F) (20):(4) + (10).(2) =
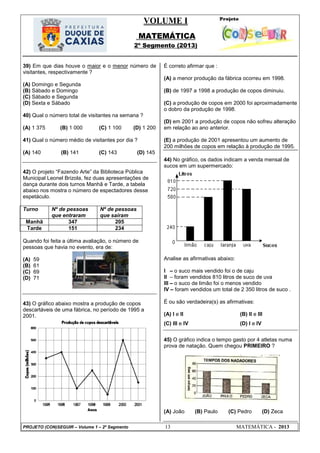
69) Observe a reta numérica abaixo:
Os números inteiros que melhor representam as
letras A, B, C e D respectivamente são:
(A) 4 ; 6 ; 1 e 1 (B) 6 ; 4 ; 1 e 1
(C) -6 ; 1 ; 1 e 4 (D) 6 ; 1 ; 1 e 4
70) Os números -2 e -1 ocupam na reta numérica
abaixo as posições indicadas, respectivamente, por
quais letras?
a) P, Q
b) Q, P
c) R, S
d) S, R
71) Observe o extrato da conta bancária e complete,
dia a dia, o saldo bancário:
Data Crédito Débito Saldo
01/02 XXXXX XXXXX 800,00
02/02 0,00 600,00
03/02 0,00 500,00
04/02 400,00 0,00
06/02 0,00 250,00](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-27-320.jpg)














![VOLUME I
MATEMÁTICA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 36 MATEMÁTICA - 2013
Temperatura mínima:
Temperatura máxima:
MULTIPLICAÇÃO DE NÚMEROS INTEIROS
→ Regras para MULTIPLICAÇÃO de Inteiros
Ex:
a) (+5) . (+6) = + 30 b) (+5) . (–6) = – 30
c) (–5) . (+6) = – 30 d) (–5) . (–6) = + 30
DIVISÃO DE NÚMEROS INTEIROS
A regra de sinais para dividir inteiros é a mesma da
multiplicação.
Ex:
a) (+ 30) : (+6) = + 5
d) (+ 30) : (–6) = – 5
d) (– 30) : (+6) = – 5
d) (– 30) : (–6) = + 5
Ex5:
Sr. José comprou pneus para o carro numa de
terminada loja através de débito automático em conta
corrente. Essa é uma forma de pagamento em que a
prestação é diretamente descontada do saldo da conta
bancária. Se o pagamento for efetuado em 5 parcelas
mensais iguais de R$138,00, qual será o débito total
em sua conta?
Nesse caso temos (+5) x (138,00) = 690,00
O débito será de R$ 690,00, ou seja, ocorrerá o
lançamento total de – R$ 690,00 em sua conta
corrente.
Ex6:
Sem condições para quitar sua dívida de R$
1651,00 com o banco, Sr. Pedro pediu o parcelamento
da mesma em 12 vezes iguais. Se esse parcelamento
resultou num acréscimo total da dívida de R$ 113,00,
qual será o valor de cada parcela a ser debitada de sua
conta corrente?
Situação antes do parcelamento: 1651
Situação após o parcelamento: 1651 + (113) =
= 1651 113 = 1764
Cálculo da divisão:
1764 I 12
-12 147
56
-48
84
-84
0
Valor das parcelas: (1764) : (+12) = 147
Logo, sua conta terá 12 débitos de R$147,00.
EXERCÍCIOS DE FIXAÇÃO
138) Resolva as expressões abaixo:
a) 17 45 =
b) 23 32 + 19 =
c) 67 86 + 75 =
d) 109 + 5 .( 8) (29) =
e) 21 : (3 – 10) + 2 . (66 : 11 13) =
f) 23 [ 4 5 + 3 . (2 4) - 8] (25) =
g) 5 + 3.(8) {56 : [4 4] - 2 . [10 + (5 5)]} =
139) Que frio! Você achou as temperaturas de Nova
York (Ex2) baixas? Então veja a previsão obtida no
mesmo site, referente ao mesmo dia em questão, só
que para a cidade de Moscou (Rússia):
Calcule a diferença entre as temperaturas
máxima e mínima.
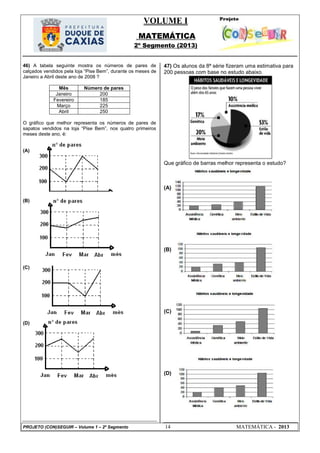
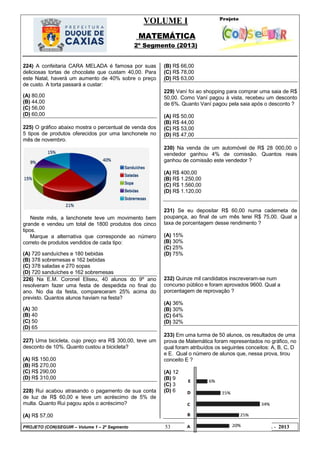
140) A tabela a seguir nos apresenta os sete modelos
de automóveis mais vendidos no Brasil em 2010 e o
respectivo número total de unidades vendidas de cada
um deles nesse mesmo ano:](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-42-320.jpg)





























































![VOLUME I
LÍNGUA PORTUGUESA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 108 LÍNGUA PORTUGUESA - 2013
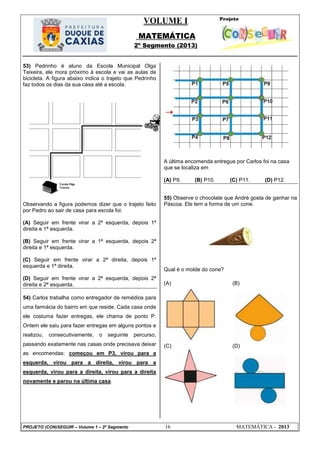
29)
Níquel Náusea. Disponível em www.niquel.com.br. Acesso em agosto de 2010.
O filhote percebe que Níquel Náusea não sabe ler, porque:
(A) Níquel Náusea substitui as personagens da história.
(B) Níquel Náusea altera as ações das personagens da história.
(C) Níquel Náusea inverte a sequência da história.
(D) Níquel Náusea recria o final da história.
30) TEXTO I
IBGE: BRASIL NÃO TEM DEPÓSITOS DEFINITIVOS PARA LIXO RADIOATIVO
1
5
10
O Instituto Brasileiro de Geografia e Estatística (IBGE) lançou o livro ―Indicadores de
Desenvolvimento Sustentável 2008 (IDS 2008)‖. Nele, os pesquisadores constataram que apesar de
produzir 13.775 metros cúbicos de resíduos radioativos, o Brasil ainda não tem, com exceção do
depósito de Abadia de Goiás - que contém os rejeitos do acidente com césio — 137, ocorrido em
Goiânia, em 1987—, depósitos finais para onde encaminhar esse material perigoso com segurança.
(...)
―É como se as pessoas guardassem rejeito radioativo tóxico em casa. Por mais que o
mantenham em segurança, o ideal é que o rejeito radioativo vá para o local no qual será, definitivamente,
armazenado‖, explicou o pesquisador Judicael Clevelário, da Coordenação dos Recursos Naturais do
IBGE.
Segundo o pesquisador, a questão é polêmica e envolve decisões políticas. ―Você deve colocar
[o rejeito radioativo] em um local onde possa vigiá-lo, para ver o que está acontecendo, intervindo
quando necessário, e ao mesmo tempo longe do alcance das pessoas. Aí entra a questão de quem quer
um depósito perto de sua casa? Essa questão ainda não foi resolvida pelos canais responsáveis‖, disse.
Disponível em http://www.saudeemmovimento.com.br/reportagem/noticia_exibe.asp?cod_noticia=2652.
Acesso em agosto de 2010.
TEXTO II
Níquel Náusea. Disponível em www.nquel.com.br. Acesso em agosto de 2010.](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-115-320.jpg)







![VOLUME I
LÍNGUA PORTUGUESA
2º Segmento (2013)
PROJETO (CON)SEGUIR – Volume 1 – 2º Segmento 116 LÍNGUA PORTUGUESA - 2013
20
seriamente o tratamento de algumas doenças de homens e animais. Isto ocorre porque muitos cultivos
possuem genes de resistência antibiótica. Se o gene resistente atingir uma bactéria nociva, pode conferir-lhe
imunidade ao antibiótico, aumentando a lista, já alarmante, de problemas médicos envolvendo doenças
ligadas a bactérias imunes', cita o relatório.
Simone Corinn ainda alerta para o fato da empresa Monsanto estar criando uma crise de
dependência no consumidor: 'As sementes da Monsanto contém um gene chamado ‗terminator‘, que faz
com que a soja não germine após algum tempo', ela explica. 'Isso obriga o produtor a comprar os produtos
novamente, sem poder estocar uma parte da safra deste ano para o plantio da safra seguinte'.
Disponível em http://revistagloborural.globo.com/Globo
Rural/ 0,6993,EEC354955-1641,00.html. Acesso em agosto de 2010.
Segundo o texto, os alimentos transgênicos são prejudiciais ao homem porque:
(A) podem aumentar a resistência de bactérias.
(B) podem ocasionar prejuízos para a agricultura.
(C) podem aumentar a resistência a bactérias.
(D) podem alterar produtos de grandes marcas alimentícias.
44)
―[...] Porque... assim, com a pessoa que você tá de repente, porque tem vezes que você tá ficando, tá ficando, tá
ficando, e aí de repente você já tá até namorando, com aquela pessoa, se você encontra com ela todo dia e tal,
mas nunca chega um amigo e fala ‗Ah, essa é sua namorada?‘, e tal, você fala, ‗É‘, ele fala, ‗É minha namorada‘,
‗É meu namorado‘‖ [...].
CHAVES, Jaqueline. ―Ficar com‖: um novo código entre jovens. Rio de Janeiro: Revan, 2001.
No texto, a palavra ―você‖ indica uma referência
(A) ao leitor.
(B) a uma pessoa relatada.
(C) ao entrevistador.
(D) a uma pessoa indeterminada.
45)
1
5
Bezerro de vaca preta
Onça pintada não come...
Quem casa com muié feia
Não tem medo de outro home.
Meu fio, muié bonita
De duas faia uma tem:
Ou qué bem a toda gente
Ou não gosta de ninguém.
FALCI, Miridan Konox. Mulheres do sertão nordestino. In: DEL PRIORE, Mary (org.)
HIstória das mulheres no Brasil. São Paulo: Contexto, 2004.(Adaptado.)
No texto, a rima entre as palavras ―come‖ e ―home‖ justifica-se por:
(A) uma incorreção na pronúncia.
(B) uma marca da oralidade.
(C) um registro informal da escrita.
(D) uma variação regional da língua.](https://image.slidesharecdn.com/volume12segmentoconseguirfinal-160210182709/85/Volume-1-2-segmento-conseguir-final-123-320.jpg)




































