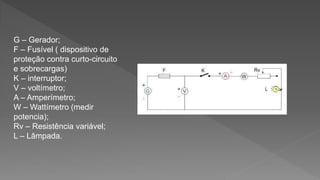
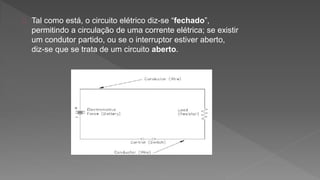
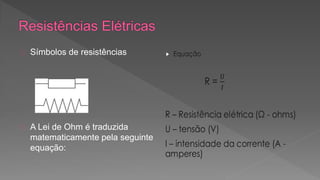
1) O documento descreve os componentes básicos de um circuito elétrico, incluindo gerador, condutores, receptores e dispositivos de proteção e medição. 2) São apresentados diferentes tipos de circuitos elétricos, como circuitos fechados, abertos e curto-circuitos. 3) A resistência elétrica é explicada como a oposição dos receptores ao fluxo de corrente elétrica, e a Lei de Ohm é usada para calcular valores de tensão, corrente e resistência.

2. O circuito elétrico consiste no conjunto de componentes,
constituído por um ou mais geradores, ligados de forma
correta para alimentar os recetores elétricos.
Os circuitos elétricos podem ter:
› Fonte de alimentação ou gerador;
› Condutores e isoladores elétricos;
› Aparelhos de proteção, comando e corte;
› Aparelhos de medição;
› Recetores.

3. G – Gerador;
F – Fusível ( dispositivo de
proteção contra curto-circuito
e sobrecargas)
K – interruptor;
V – voltímetro;
A – Amperímetro;
W – Wattímetro (medir
potencia);
Rv – Resistência variável;
L – Lâmpada.

4. Considerando um circuito que contem uma bateria como fonte de energia
(introduz uma força eletromotriz no circuito), uma carga (Resistência) e um
interruptor, interligados por condutores elétricos.

5. Tal como está, o circuito elétrico diz-se “fechado”,
permitindo a circulação de uma corrente elétrica; se existir
um condutor partido, ou se o interruptor estiver aberto,
diz-se que se trata de um circuito aberto.

6. Se estabelecermos uma ligação entre
dois pontos (a vermelho) com um
elemento condutor, provocamos uma
corrente elétrica de intensidade muito
elevada. Diz-se que provocamos um
curto-circuito (resistência global do
circuito quase nula). Por efeito desta
corrente, podem ocorrer danos nos
componentes do circuito se as
proteções não atuarem (fusíveis,
disjuntores, etc...)

7. Quando um gerador alimenta por exemplo uma torradeira, um televisor ou
outro eletrodoméstico, estes são percorridos por uma determinada
intensidade de corrente, sabe-se que, apesar de alimentados pela mesma
tensão, a intensidade de corrente é diferente de recetor para recetor.
Entende-se por recetores todo o equipamento que absorve energia elétrica,
produzindo trabalho. Os recetores mais comuns são:

8. Iluminação – Lâmpadas;
Aquecimento – Aquecedores, ferros de engomar, torradeiras, etc.
Força motriz – maquina de lavar, aspiradores, ventoinhas, batedeiras, etc.
Sinalização – Campainhas, buzinas, etc.
Eletroquímicos – Pilhas e acumuladores

9. Cada aparelho (recetor) oferece uma oposição diferente à passagem dos
eletrões (corrente elétrica). Esta oposição, maior ou menor, tem a ver com o
material (condutor) do recetor e com as próprias dimensões (secção e
comprimento) do mesmo material.
A esta oposição do recetor à passagem dos eletrões dá-se o nome de
Resistência Elétrica e é dada em ohm (Ω).

10. Quanto maior for a resistência elétrica do recetor, tanto menor será a
intensidade da corrente I que o percorre.
A resistência tem múltiplos e submúltiplos: Megaohm (MΩ), sendo
1 MΩ = 1000 000 Ω = 106 Ω

11. Símbolos de resistências
A Lei de Ohm é traduzida
matematicamente pela seguinte
equação:

12. A partir da expressão anterior da Lei de Ohm, podemos
obter:
푅 =
푈
퐼
 I=
푈
푅
 푈 = 푅. 퐼
Assim, conhecendo o valor de R, podemos calcular os valores
de I para diferentes valores de U aplicados ou podemos
calcular os valores da tensão U aplicada ao recetor para
diferentes valores de intensidade.

13. 1. Uma resistência linear é percorrida por uma intensidade de
0,3 A quando submetida a uma tensão de 24V. Calcule:
a) O valor da resistência.
R =
푈
퐼
=
24
0,3
= 80 

14. b) O valor da intensidade que ela absorveria se lhe
aplicássemos uma tensão de 15V.
퐼 =
푈
푅
=
15
80
= 0,19 A

15. 2. Uma resistência elétrica absorve 3 A quando ligada a 230 V.
Calcule o valor da tensão que lhe é aplicada quando ela
absorve 1,2 A.
푅 =
푈
퐼
=
230
3
= 76,7 
U = R * I = 76,7 * 1,2 = 92 v

16. 3. Uma dada resistência de aquecimento de 50  é normalmente
ligada a 230 V. Calcule o valor da resistência que deveria ser
acrescentada de modo que ela absorvesse 3 A da rede.
4. Um reóstato tem indicado na sua chapa de características os
seguintes valores: 200  e 1,3 A. Calcule:
a) A tensão máxima que se lhe pode aplicar.
b) A intensidade que absorve, se lhe aplicarmos 120 V.
c) O valor da tensão que se lhe deve aplicar para que ele absorva 0,4 A.

17. 5. Uma dada resistência elétrica absorve 0,5 A. Ao
aumentarmos a resistência total para 100 , esta passou a
absorver 0,2 A. Calcule:
a) A tensão aplicada.
b) A resistência inicial.

19. Resistências de maiores dimensões como as bobinadas ou
as resistências de cápsula cerâmica têm os seus valores de
resistência e de tolerância impressos no seu corpo. As
resistências menores, como as de carbono moldado ou as
de película metálica, são geralmente demasiado pequenas
para terem os valores impressos. Por isso, são geralmente
cobertas por uma camada de epoxy ou dum material
semelhante, no qual são impressas várias bandas coloridas
de forma radial.

20. As bandas de cores permitem determinar o valor da
resistência, da tolerância, do coeficiente de temperatura e,
por vezes, da fiabilidade do componente. São sempre lidas a
partir da esquerda, definindo-se a esquerda como o lado do
componente que tiver uma banda mais próxima.

21. O código de cores varia conforme as resistências sejam
normais ou de precisão: as resistências normais são
codificadas com quatro bandas, ao passo que as de precisão
são codificadas com base num código de cinco bandas.

25. Qual o valor das resistências cujas cores são:
› Castanho, preto, vermelho?
› Cinza, vermelho, castanho?
› Laranja, branco, verde?

26. Dá o código de cores para os seguintes valores de
resistência:
› 1,8 K 
› 270 
› 56 K 
› 1 M 

27. Obtém os valores máximos e mínimos de resistências
marcadas com as seguintes faixas:
› Vermelho, vermelho, preto ----ouro
› Amarelo, violeta, amarelo ---- prata

28. Geralmente uma fonte de tensão está ligada a várias
resistências. O comportamento de uma associação de
resistências será análogo ao de uma única resistência, que
se designa por resistência equivalente.
As resistências podem ser:
› Série – tem apenas um terminal comum ou seja, um terminal de um
deles está ligado a um só terminal do outro.
› Paralelo – tem dois pontos em comum.

29. Num circuito em série existe somente um caminho para os
eletrões, logo estes terão de percorrer todos os
componentes constituintes deste.
Num circuito em paralelo existem vários caminhos para os
eletrões, a maior quantidade destes percorrerá o caminho
com menos oposição.

30. A resistência equivalente ou resistência total no circuito em
série é dada por:
Rt = R1 + R2 + R3 + … + Rn
A resistência equivalente ou resistência total no circuito em
paralelo é dada por:
1
푅푡
=
1
푅1
+
1
푅2
+
1
푅3
+ … +
1
푅푛

31. Chama-se condensador a todo o sistema formado por dois
condutores (armaduras) separadas por um isolante de
pequena espessura (dielétrico).
São elementos passivos que apresentam uma relação linear
entre a variação de tensão e a corrente. Acumulam carga
elétrica. A capacidade é a razão entre a carga acumulada e a
tensão aos terminais do condensador.

33. A capacidade depende do tamanho e forma dos condutores e da
sua localização mútua. No caso de um condensador de placas
paralelas a capacidade é dada pela seguinte fórmula:
퐶 =
푄
푈
=
퐶표푢푙표푚푏푠
푉표푙푡푠
= 퐹푎푟푎푑
C – capacidade (Farad)
Q – carga elétrica (C)
U – tensão aplicada (V)

34. Calcule a carga acumulada num condensador de 1000 μF
sendo a diferença de potencial entre os seus terminais de 50
V.
Q = 1000 x 10 -6 F x 50 V = 50000 μ C = 50 mC

35. É importante lembrar que os valores em múltiplos ou submúltiplos devem
ser convertidos para a unidade, preferencialmente usando potências de
dez. Assim, 1 μF equivale a 1 x 10-6 F. Os resultados podem ser
apresentados em potências de dez ou em submúltiplos/múltiplos. As
potências de dez dos submúltiplos do Farad são:
› Microfarad - 1 μF = 1 x 10-6 F
› Nanofarad - 1 nF = 1 x 10-9 F
› Picofarad - 1 pF = 1 x 10-12 F

36. Os fatores que afetam a capacidade são:
› a área das placas (armaduras);
› a distância entre as placas (armaduras);
› o tipo de dielétrico (isolante).
Quanto maior for a área das placas, mais carga será
acumulada para uma dada tensão; portanto, maior será a
capacidade. Quanto mais isolante o meio for, mais cargas
serão acumuladas e consequentemente maior será a
capacidade.

37. Podemos então apresentar a seguinte fórmula para o cálculo da
capacidade de um condensador de placas paralelas e idênticas,
com dielétrico uniforme:
퐶 =
휀0 휀푟 퐴
푑
C é a capacidade em Farads
휀0 é a constante dielétrica do vácuo, igual a 8,85 x 10-12 F/m (Farads por metro).
휀r é a constante dielétrica relativa do material isolante (indica quantas vezes o material é mais
isolante que o vácuo, logo não tem unidade).
A é a área de cada placa (se forem idênticas e sobrepostas) ou a área comum às placas, em
m2 (metros quadrados).
d é distância entre as placas ou a espessura do isolante (dielétrico), em m (metros).

38. Mais uma vez, é importante destacar que, ao introduzir na
fórmula, todos os valores têm de ser expressos na unidade,
preferencialmente usando potências de dez.

40. Calcule a capacidade do condensador ilustrado a seguir, formado por
placas idênticas com lado igual a 10 centímetros e dielétrico de uma folha
de papel parafinado com meio milímetro de espessura.
Lado l = 10 cm = 0,1 m
A = 0,1 m x 0,1 m = 10 -2 m2
Distância d = 0,5 mm = 0,5 x 10 -3 m
C = 8,85 x 10 -2 F/m x 2,5 x 10 -2 m2/ 10 -3 m
C = 221, 25 x 10 -12 F = 221,25 pF

41. As funções que pode desempenhar num circuito são as de
bloqueio (da componente elétrica de um sinal), filtragem (de
determinadas frequências), armazenamento de cargas
elétricas, acoplamento ou desacoplamento (entre partes do
circuito eletrónico), correção do fator de potência do circuito,
eliminação de ruídos, etc.

42. Cerâmico – valores pequenos (até 1 μF), tensões elevadas,
bom funcionamento

43. Poliéster – propriedades semelhantes aos cerâmicos e
valores mais elevados (até 10 μF)

44. Eletrolítico– polarizados. Valores elevados mas de baixa
precisão e estabilidade com a temperatura. Têm baixo
desempenho.

45. Tântalo – polarizados. Maior capacidade volumétrica e
melhor desempenho que os eletrolíticos. Baixas tensões.
Dispendiosos.

46. 퐶 =
푄
푈
Série de valores básicos de condensadores (valores
comerciais):
10 12 15 18 22 27 33 39 47 56 68 82
Os múltiplos e submúltiplos decimais destes valores básicos
permitem encontrar os valores dos condensadores.

47. Exemplos:
(para o número básico 10): 1pF – 10pF – 100pF – 1 nF – 10 nF –
100 nF – 1 μF – 10 μF – 100 μF – 1000 μF
(para o número básico 22): 2,2 pF – 22 pF – 220 pF – 2,2 nF – 22
nF – 220 nF – 2,2 μF – 22 μF – 220 μF – 2200 μF
(para o número básico 47): 4,7 pF – 47 pF – 470 pF – 4,7 nF – 47
nF – 470 nF – 4,7 μF – 47 μF – 470 μF – 4700 μF

48. O código de cores para os condensadores é, em parte,
semelhante ao código das resistências. A principal diferença
são as unidades. Enquanto que nas resistências a unidade
principal é o Ohm (), nos condensadores a unidade
principal é o picoFarad (pF).

49. Exemplo:
Se um condensador cerâmico tiver a
sequência de cores:
1ª Banda: Verde
2ª Banda: Azul
Multiplicador: Vermelho
Tolerância: Verde
Resultado:
C = 56 x 102 pF = 5600 pF
Tolerância = +- 5%
Cmin = C + (C x Tolerância) = 5600 x 10-
12 – (5600 x 10-12 x 0,05) = 5320 pF
C max = C + (C x Tolerância) = 5600 x 10-
12 + (5600 x 10-12 x 0,05) = 5880 pF

51. A marcação dos valores dos condensadores de menos de 10
pF é feita usando na “terceira posição”, um algarismo “9”,
cujo significado é dividir por 10 o número formado pelos dois
algarismos anteriores.
Exemplos para condensadores:
› Inscrito no condensador: 479  47/10  4,7 pF
› Inscrito no condensador: 159  15/10  1,5 pF

53. Qual o valor das capacidades dos condensadores:
› 203M
› 102F
› 10KH
› 11KK

54. O coeficiente de temperatura "TC" define a variação da
capacidade dentro de uma determinada faixa de
temperatura. O "TC" é normalmente expresso em % ou
ppm/°C (partes por milhão / °C). É usado uma sequência de
letras ou letras e números para representar os coeficientes.
Observa o desenho abaixo.

55. Na tabela abaixo estão alguns coeficientes de temperatura e
as tolerâncias que são muito utilizadas por diversos
fabricantes de condensadores.

56. Outra forma de representar coeficientes de temperatura é
mostrado abaixo. É usada em condensadores que se
caracterizam pela alta capacidade por unidade de volume
(dimensões reduzidas) devido a alta constante dielétrica.

58. Associação em paralelo
Como em toda associação em paralelo, a tensão é a mesma em todos os seus
ramos. Logo, cada condensador de uma associação em paralelo fica
submetido à mesma tensão que é aplicada ao conjunto (V).
V = V1 = V2 = V3 = ... = Vn

59. Sendo V1 a tensão no condensador C1, V2 a tensão no
condensador C2 e Vn a tensão no condensador Cn (Cn é um
condensador qualquer da associação, não importando quantos
condensadores estejam associados).
Já a capacidade equivalente de uma associação de
condensadores em paralelo é a soma das capacidades
individuais dos ramos.
Ceq = C1 + C2 + C3 + ... + Cn

60. Sendo C1 a capacidade do primeiro condensador, C2 a
capacidade do segundo condensador e Cn a capacidade de
um condensador qualquer da associação, não importando
quantos condensadores estejam associados.
A carga em cada condensador da associação pode ser
facilmente calculada pela equação Q = C x U, sendo C a
capacidade desse condensador e U a tensão total, pois é a
mesma em cada um.

61. A carga total da associação é a soma das cargas individuais
dos condensadores e também pode ser calculada pelo produto
da capacidade equivalente da associação pela tensão total.
QTOTAL = Q1 + Q2 + Q3 + ... + Qn
ou
QTOTAL = Ceq x V

62. Associação em série
A grandeza comum a todos os elementos de uma associação em série é a
corrente. Como corrente é a quantidade de carga que atravessa o circuito (ou
se acumula nos seus componentes, como no caso dos condensadores) por
unidade de tempo, então é fácil perceber que a carga será a mesma em todos
os condensadores da associação em série.
QTOTAL = Q1 = Q2 = Q3 = ... = Qn

63. Sendo Q1 a carga no condensador C1, Q2 a carga no condensador C2 e Qn a
carga no condensador Cn (Cn é um condensador qualquer da associação, não
importando quantos condensadores estejam associados).
Sabemos que na associação em série a tensão total é a soma das tensões
individuais em seus componentes. Também sabemos que U = Q / C. Então,
podemos escrever:
UTOTAL = QT / Ceq = (QT / C1) + (QT / C2) + (QT / C3) + ... + (QT / Cn)

64. Colocando QT em evidência, vem:
QT / Ceq = QT [(1 / C1) + (1 / C2) + (1 / C3) + … + (1 / Cn)]
Dividindo os dois lados da equação por QT ela não se altera:
1 / Ceq = (1 / C1) + (1 / C2) + (1 / C3) + … + (1 / Cn)

65. Logo, já temos o valor da capacidade equivalente da
associação em série:

66. A tensão em qualquer condensador da associação em série
pode ser obtida dividindo a carga total (que também é a carga
individual, como já vimos) pela sua capacidade.

67. Num circuito formado por um condensador (C) em série com
uma resistência(R) e uma fonte de tensão (E) haverá
máxima circulação de corrente (I) no instante em que a fonte
for ligada. Como sabemos, corrente elétrica é formada por
cargas em movimento; essas cargas deslocam-se da fonte
para o condensador e nele se acumulam. Pela equação
anterior, à medida que a quantidade de carga no
condensador aumenta, aumenta a tensão sobre ele.

68. Assim, a diferença de potencial entre o condensador e a
fonte vai diminuindo e com ela a corrente, até a tensão se
tornar igual à da fonte e a corrente nula, quando o
condensador estará totalmente carregado.
Desligando a fonte, o condensador permanece carregado
por longo tempo, só perdendo carga pelo efeito da
resistência de fuga.

69. Entretanto, se em vez da fonte for colocado um fio, o
condensador perderá carga rapidamente, isto é, as cargas
em excesso numa placa passarão para a outra placa,
completando as cargas em falta e anulam-se. A corrente de
descarga, então, vai no sentido oposto ao da carga e parte
do máximo até zero, quando a tensão também chega a zero.

70. Carga do condensador Descarga do condensador

71. Todo esse processo está representado nos gráficos a seguir.
Tensão
Circulação
de corrente

72. Observamos que as curvas são exponenciais, pelo efeito já
mencionado de que as cargas já acumuladas no
condensador tendem a repelir novas cargas.
O tempo considerado para que o condensador se carregue
totalmente ou se descarregue totalmente é igual a cinco
vezes o produto da resistência pela capacidade. Esse
produto é chamado de constante de tempo e representado
pela letra grega (tau).

73. Na verdade, após 5RC a carga atinge 99.3% do valor
máximo ou mínimo, mas isso é considerado como 100%
para efeitos práticos, já que o limite somente será alcançado
no infinito.
A tensão máxima sobre o condensador, como sabemos, será
aquela aplicada pelo circuito; no caso, a tensão da fonte (E).
Já a corrente máxima, positiva ou negativa, é dada pela Lei
de Ohm: Imax = E / R.

74. 1) Calcule a capacidade de um condensador formado por
duas placas idênticas de raio 1cm separadas por uma folha
de mica com 0,1 mm de espessura.
2) Calcule a carga acumulada em um condensador de 27 nF
sendo a diferença de potencial entre os seus terminais de
100 V.
3) Calcule a tensão entre os terminais de um condensador
de 300 pF carregado com 15 pC.

75. 4) Calcule a capacidade equivalente entre os terminais A e B
do circuito abaixo, bem como a carga acumulada no
condensador de 40 nF e a tensão no condensador de 5 nF..

76. Apontamentos do professor Élvio Jesus
José V.C. Matias. Eletricidade e Eletrónica – Cursos profissionais, Volume 1.
Didática Editora
Eng. Mario R. Cruzeiro. Lições de Eletrotecnia, Volume 1
http://www.prof2000.pt/users/lpa - Lucínio Preza de Araújo
http://efisica.if.usp.br/eletricidade/basico/capacitor/assoc_condensadores/
http://pt.scribd.com/doc/7351630/Fundamentos-Da-Eletronica
http://www.eletronica24h.com.br/Curso%20CA/aparte1/aulas/aula003.html
Http://essl.home.sapo.pt/Elementos/Condensadores.htm
http://ivairsouza.com/capacitor1-site.html