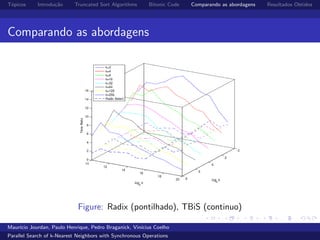
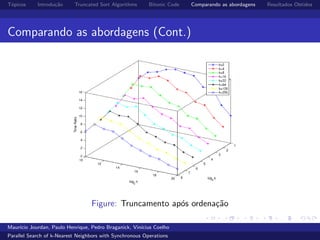
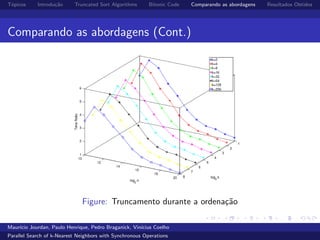
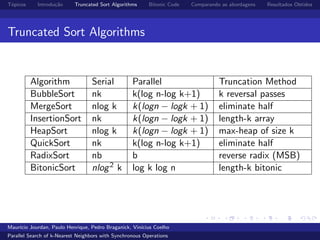
O documento compara algoritmos de ordenação truncada para busca paralela de k-vizinhos mais próximos de forma síncrona. O algoritmo BitonicSort mostrou desempenho superior ao RadixSort na ordenação, sendo de 2 a 16 vezes mais rápido, e superior também na busca completa de kNN, com desempenho de 1,3 a 4 vezes melhor.

1. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Parallel Search of k-Nearest Neighbors with
Synchronous Operations
Maur´ıcio Jourdan, Paulo Henrique,
Pedro Braganick, Vin´ıcius Coelho
Instituto de Inform´atica
Universidade Federal de Goi´as (UFG)
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

2. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
T´opicos
1 Introdu¸c˜ao
2 Truncated Sort Algorithms
3 Codifica¸c˜ao
4 Comparando as abordagens
5 Resultados Obtidos
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

3. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Introdu¸c˜ao
O artigo em quest˜ao nos mostra uma forma de localizar,
paralelamente, k-vizinhos mais pr´oximos de forma s´ıncrona em um
espa¸co vetorial atrav´es de uma arquitetura de v´arios n´ucleos
(many-core) que favorece algor´ıtmos com opera¸c˜oes s´ıncronas e de
alto custo.
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

4. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Introdu¸c˜ao
O artigo em quest˜ao nos mostra uma forma de localizar,
paralelamente, k-vizinhos mais pr´oximos de forma s´ıncrona em um
espa¸co vetorial atrav´es de uma arquitetura de v´arios n´ucleos
(many-core) que favorece algor´ıtmos com opera¸c˜oes s´ıncronas e de
alto custo.
A busca pelos vizinhos mais pr´oximos ´e feita atrav´es de sele¸c˜oes e
ordena¸c˜oes, sendo que para cada ordena¸c˜ao foi testado um
algoritmo diferente afim de classificar qual seria o mais eficiente
em dada condi¸c˜ao de vizinhos (k).
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

5. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Introdu¸c˜ao (Cont.)
A implementa¸c˜ao e desenvolvimento de algoritmos de busca por
k-vizinhos mais pr´oximos ´e importante na quest˜ao de performance
de tempo pois suas aplica¸c˜oes, na maioria dos casos, est˜ao em
ambientes onde o tempo ´e um fator cr´ıtico.
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

6. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Introdu¸c˜ao (Cont.)
A implementa¸c˜ao e desenvolvimento de algoritmos de busca por
k-vizinhos mais pr´oximos ´e importante na quest˜ao de performance
de tempo pois suas aplica¸c˜oes, na maioria dos casos, est˜ao em
ambientes onde o tempo ´e um fator cr´ıtico.
Logo, o processamento e an´alise devem ser feitas em tempo real,
tal como minera¸c˜ao de dados em imagens/v´ıdeos, detec¸c˜ao de
intrusos em uma rede, categoriza¸c˜ao de texto, entre outras
aplica¸c˜oes.
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

7. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Truncated Sort Algorithms
Algorithm Serial Parallel Truncation Method
BubbleSort nk k(log n-log k+1) k reversal passes
MergeSort nlog k k(logn − logk + 1) eliminate half
InsertionSort nk k(logn − logk + 1) length-k array
HeapSort nlog k k(logn − logk + 1) max-heap of size k
QuickSort nk k(log n-log k+1) eliminate half
RadixSort nb b reverse radix (MSB)
BitonicSort nlog2 k log k log n length-k bitonic
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

8. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
C´odigo em CUDA
1 #d e f i n e THREADS 512 // 2ˆ9
2 #d e f i n e BLOCKS 32768 // 2ˆ15
3 #d e f i n e NUM VALS THREADS∗BLOCKS
4
5 void p r i n t e l a p s e d ( c l o c k t s t a r t , c l o c k t stop ){
6 double e l a p s e d = (( double ) ( stop − s t a r t ) ) / CLOCKS PER SEC ;
7 p r i n t f ( ” Elapsed time : %.3 f s n” , e l a p s e d ) ;
8 }
9
10 f l o a t random float (){
11 return ( f l o a t ) rand () /( f l o a t )RAND MAX;
12 }
13
14 void a r r a y p r i n t ( f l o a t ∗arr , i n t l e n g t h ) {
15 i n t i ;
16 f o r ( i = 0; i < l e n g t h ; ++i )
17 p r i n t f ( ”%1.3 f ” , a r r [ i ] ) ;
18 p r i n t f ( ”n” ) ;
19 }
20
21 void a r r a y f i l l ( f l o a t ∗arr , i n t l e n g t h ){
22 srand ( time (NULL) ) ;
23 i n t i ;
24 f o r ( i = 0; i < l e n g t h ; ++i )
25 a r r [ i ] = random float () ;
26 }
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

9. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
C´odigo em CUDA (Cont.)
1 g l o b a l void b i t o n i c s o r t s t e p ( f l o a t ∗dev values , i n t j , i n t k ){
2 unsigned i n t i , i x j ; /∗ S o r t i n g p a r t n e r s : i and i x j ∗/
3 i = t h r e a d I d x . x + blockDim . x ∗ b l o c k I d x . x ;
4 i x j = i ˆ j ;
5
6 /∗ The t h r e a d s with the l owest i d s s o r t the a r r a y . ∗/
7 i f (( i x j )>i ) {
8 i f (( i&k )==0) {
9 /∗ Sort ascending ∗/
10 i f ( d e v v a l u e s [ i ]> d e v v a l u e s [ i x j ] ) {
11 /∗ exchange ( i , i x j ) ; ∗/
12 f l o a t temp = d e v v a l u e s [ i ] ;
13 d e v v a l u e s [ i ] = d e v v a l u e s [ i x j ] ;
14 d e v v a l u e s [ i x j ] = temp ;
15 }
16 }
17 i f (( i&k ) !=0) {
18 /∗ Sort descending ∗/
19 i f ( d e v v a l u e s [ i ]< d e v v a l u e s [ i x j ] ) {
20 /∗ exchange ( i , i x j ) ; ∗/
21 f l o a t temp = d e v v a l u e s [ i ] ;
22 d e v v a l u e s [ i ] = d e v v a l u e s [ i x j ] ;
23 d e v v a l u e s [ i x j ] = temp ;
24 }
25 }
26 }
27 }
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

10. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
C´odigo em CUDA (Cont.)
1 void b i t o n i c s o r t ( f l o a t ∗ v a l u e s ){
2 f l o a t ∗ d e v v a l u e s ;
3 s i z e t s i z e = NUM VALS ∗ s i z e o f ( f l o a t ) ;
4
5 cudaMalloc (( void ∗∗) &dev values , s i z e ) ;
6 cudaMemcpy ( dev values , values , s i z e , cudaMemcpyHostToDevice ) ;
7
8 dim3 b l o c k s (BLOCKS, 1 ) ; /∗ Number of b l o c k s ∗/
9 dim3 t h r e a d s (THREADS, 1 ) ; /∗ Number of t h r e a d s ∗/
10
11 i n t j , k ;
12 /∗ Major step ∗/
13 f o r ( k = 2; k <= NUM VALS; k <<= 1) {
14 /∗ Minor step ∗/
15 f o r ( j=k>>1; j >0; j=j >>1) {
16 b i t o n i c s o r t s t e p <<<blocks , threads >>>(dev values , j , k ) ;
17 }
18 }
19 cudaMemcpy ( values , dev values , s i z e , cudaMemcpyDeviceToHost ) ;
20 cudaFree ( d e v v a l u e s ) ;
21 }
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

11. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
C´odigo em CUDA (Cont.)
1 i n t main (){
2 c l o c k t s t a r t , stop ;
3
4 f l o a t ∗ v a l u e s = ( f l o a t ∗) malloc ( NUM VALS ∗ s i z e o f ( f l o a t ) ) ;
5 a r r a y f i l l ( values , NUM VALS) ;
6
7 s t a r t = c l o c k () ;
8 b i t o n i c s o r t ( v a l u e s ) ; /∗ I n p l a c e ∗/
9 stop = c l o c k () ;
10 p r i n t e l a p s e d ( s t a r t , stop ) ;
11 }
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

12. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Comparando as abordagens
Figure: Radix (pontilhado), TBiS (continuo)
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

13. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Comparando as abordagens (Cont.)
Figure: Truncamento ap´os ordena¸c˜ao
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

14. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Comparando as abordagens (Cont.)
Figure: Truncamento durante a ordena¸c˜ao
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

15. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Resultados Obtidos
Pode-se observar nos testes que o uso do BitonicSort durante o
processo de ordena¸c˜ao necess´ario para a busa kNN foi de 2 a 16
vezes mais r´apido que o uso do RadixSort no mesmo processo (sem
o c´alculo da distˆancia).
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

16. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Resultados Obtidos
Pode-se observar nos testes que o uso do BitonicSort durante o
processo de ordena¸c˜ao necess´ario para a busa kNN foi de 2 a 16
vezes mais r´apido que o uso do RadixSort no mesmo processo (sem
o c´alculo da distˆancia).
Com o c´alculo de distˆancia (utilizando CUBLAS em ambos), o
BitonicSort apresentou desempenho de 1,3 a 4 vezes superior.
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations

17. T´opicos Introdu¸c˜ao Truncated Sort Algorithms Bitonic Code Comparando as abordagens Resultados Obtidos
Resultados Obtidos (Cont.)
Analisando os gr´aficos, observou-se que o Bitonic e o RadixSort
apresentam basicamente o mesmo gasto de tempo para
transferˆencia de dados e c´alculo da distˆancia. Entretanto, na
ordena¸c˜ao o Bitonic apresentou o resultado acima mencionado.
Maur´ıcio Jourdan, Paulo Henrique, Pedro Braganick, Vin´ıcius Coelho
Parallel Search of k-Nearest Neighbors with Synchronous Operations