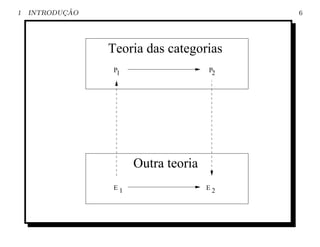
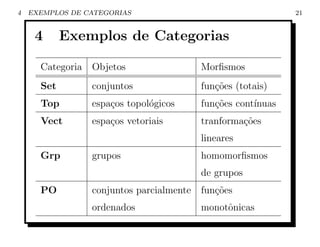
Este documento introduz a Teoria das Categorias. Ele define o que são categorias, objetos e morfismos. Também explica o que são diagramas e identidade e composição de morfismos. Por fim, fornece exemplos de categorias como Conjuntos, Espaços Topológicos, Espaços Vetoriais e Grupos.

1. 1
Teoria das Categorias: uma introdu¸˜o
ca
Prof. Carlos A. P. Campani
8 de mar¸o de 2006
c

2. 2
Copyright c 2005 Carlos A. P. Campani.
´
E garantida a permiss˜o para copiar, distribuir e/ou
a
modificar este documento sob os termos da Licen¸a de
c
Documenta¸ao Livre GNU (GNU Free Documentation
c˜
License), Vers˜o 1.2 ou qualquer vers˜o posterior
a a
publicada pela Free Software Foundation; sem Se¸oes
c˜
Invariantes, Textos de Capa Frontal, e sem Textos de
Quarta Capa. Uma c´pia da licen¸a ´ inclu´ na se¸ao
o c e ıda c˜
intitulada “GNU Free Documentation License”.
veja: http://www.ic.unicamp.br/~norton/fdl.html.

3. 3
Bibliografia
• ASPERTI, A. ; LONGO, G. Categories Types and
Structures: an introduction to Category Theory for
the working computer scientist. MIT Press, 1991.
Dispon´ em: ftp://ftp.di.ens.fr/pub/users/
ıvel
longo/CategTypesStructures/book.pdf.
• MENEZES, P. ; HAEUSLER, E. Teoria das
Categorias para Ciˆncia da Computa¸˜o. Editora
e ca
Sagra Luzzatto, 2001.
• MAC LANE, S. Categories for the Working
Mathematician, Springer-Verlag, 1971.

4. 1 ¸˜
INTRODUCAO 4
1 Introdu¸˜o
ca
• Teoria das Categorias estuda “objetos” e
“morfismos” entre eles;
• Ela ´ uma generaliza¸ao da teoria dos conjuntos e
e c˜
das fun¸oes:
c˜
– Objetos = Conjuntos estruturados;
– Morfismos = “fun¸˜es”;
co

5. 1 ¸˜
INTRODUCAO 5
• Fornece uma ferramenta para a descri¸˜o abstrata de
ca
problemas de matem´tica;
a
• Fornece um jarg˜o matem´tico e um ambiente
a a
matem´tico consistente e unificado para a
a
investiga¸ao em matem´tica;
c˜ a

6. 1 ¸˜
INTRODUCAO 6
Teoria das categorias
P1 P2
Outra teoria
E1 E2

7. 1 ¸˜
INTRODUCAO 7
• A capacidade de generaliza¸ao, abstra¸˜o e unifica¸ao
c˜ ca c˜
s˜o os principais m´ritos de Teoria das Categorias;
a e
• A relevˆncia de Teoria das Categorias para Ciˆncia
a e
da Computa¸ao ´ que Teoria da Computa¸ao, assim
c˜ e c˜
como Teoria das Categorias, ´ uma “teoria das
e
fun¸˜es”;
co
• Fornece uma estrutura para o estudo de semˆntica de
a
linguagens de programa¸ao.
c˜

8. 2 ¸˜
DEFINICAO DE CATEGORIA 8
2 Defini¸˜o de Categoria
ca
• A unica opera¸ao b´sica de Teoria das Categorias ´ a
´ c˜ a e
composi¸˜o;
ca
• Exige-se que a composi¸ao seja associativa e que
c˜
exista uma identidade para todos os objetos;

9. 2 ¸˜
DEFINICAO DE CATEGORIA 9
Uma categoria C ´:
e
1. Uma cole¸ao ObC de objetos, denotados por
c˜
a, b, . . . , A, B, . . .;
2. Uma cole¸ao MorC de morfismos (setas), denotadas
c˜
por f, g, . . .;
3. As opera¸˜es dom e cod atribuindo para cada seta f
co
dois objetos, respectivamente dom´nio (origem) e
ı
codom´nio (destino) de f ;
ı

10. 2 ¸˜
DEFINICAO DE CATEGORIA 10
4. Uma opera¸˜o id associando a cada objeto b um
ca
morfismo idb (a identidade de b) tal que
dom(idb ) = cod(idb ) = b;
5. Uma opera¸˜o ◦ (composi¸˜o) associando a cada par
ca ca
de setas f e g, com dom(f ) = cod(g) uma seta f ◦ g
tal que dom(f ◦ g) = dom(g) e cod(f ◦ g) = cod(f ).

11. 2 ¸˜
DEFINICAO DE CATEGORIA 11
Identidade e composi¸˜o devem satisfazer:
ca
Lei da identidade Para quaisquer setas f e g, tal que
cod(f ) = dom(g) = b, idb ◦ f = f e g ◦ idb = g;
Lei da associatividade Para quaisquer setas f , g e h,
tal que dom(f ) = cod(g) e dom(g) = cod(h),
(f ◦ g) ◦ h = f ◦ (g ◦ h).

12. 2 ¸˜
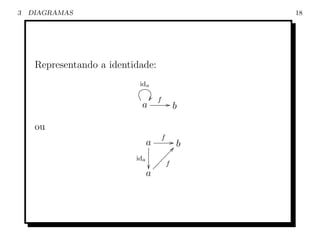
DEFINICAO DE CATEGORIA 12
Nota¸ao:
c˜
• f : a → b denota um morfismo com origem a e
destino b;
• Dados dois objetos a e b, o conjunto de todos os
morfismos f tal que f : a → b ´ denotado por C[a, b].
e
Assim, f ∈ C[a, b] significa que dom(f ) = a e
cod(f ) = b.

13. 2 ¸˜
DEFINICAO DE CATEGORIA 13
Observa¸˜o: Pela defini¸ao de categoria, todo objeto
ca c˜
b ∈ ObC deve possuir uma identidade idb : b → b, e esta
identidade ´ unica pois se existisse uma idb = idb ent˜o,
e´ a
pela lei da identidade, idb = idb ◦ idb = idb .

14. 2 ¸˜
DEFINICAO DE CATEGORIA 14
• Um morfismo em que coincidem origem e destino ´
e
chamado de endomorfismo;
• Uma categoria C ´ pequena se ObC e MorC s˜o
e a
conjuntos. Caso contr´rio a categoria ´ dita grande.
a e

15. 3 DIAGRAMAS 15
3 Diagramas
• Diagramas s˜o usados para representar equa¸˜es;
a co
• Permitem inferir novas equa¸oes a partir de outras j´
c˜ a
conhecidas.

16. 3 DIAGRAMAS 16
f
a Gb
Onde: a, b – objetos;
f : a → b – morfismo.

17. 3 DIAGRAMAS 17
Exemplo: Sejam os morfismos f : a → b, g : a → c e
h : c → b, ent˜o seu diagrama ´:
a e
f
ab Gb
bb y
bb
g bb h
b
1
c

18. 3 DIAGRAMAS 18
Representando a identidade:
ida
Ô f
a Gb
ou
f
a Gb
ÐÐd
ÐÐ
ida
ÐÐ f
ÐÐ
a

19. 3 DIAGRAMAS 19
Um diagrama comuta se a composi¸˜o dos morfismos ao
ca
longo de qualquer caminho entre dois objetos fixos ´
e
igual.

20. 3 DIAGRAMAS 20
Lei associativa:
h Gb
a
ÑÑÑ
ÑÑÑg
ÐÑÑ
c Gd
f
f : c → d g : b → c h : a → b (f ◦ g) ◦ h = f ◦ (g ◦ h)
Lei da identidade:
f
b bb Ga
bb
bb bb g
bb a
id bb
f bb bb
0 1
a Gc
g
f : b → a g : a → c ida ◦ f = f g ◦ ida = g

21. 4 EXEMPLOS DE CATEGORIAS 21
4 Exemplos de Categorias
Categoria Objetos Morfismos
Set conjuntos fun¸˜es (totais)
co
Top espa¸os topol´gicos
c o fun¸˜es cont´
co ınuas
Vect espa¸os vetoriais
c tranforma¸˜es
co
lineares
Grp grupos homomorfismos
de grupos
PO conjuntos parcialmente fun¸˜es
co
ordenados monotˆnicas
o

22. 4 EXEMPLOS DE CATEGORIAS 22
Sobre Set:
• Para comprovar que Set ´ uma categoria basta
e
verificar a associatividade de fun¸oes e a identidade;
c˜
• Dados f : A → B, g : B → C e h : C → D, e para
qualquer a ∈ A:
((h ◦ g) ◦ f )(a) = (h ◦ g)(f (a)) =
= h(g(f (a))) = h(g ◦ f (a)) = (h ◦ (g ◦ f ))(a)
• Para qualquer f : A → B e para qualquer a ∈ A:
(f ◦ idA )(a) = f (idA (a)) = f (a) = b = idB (b) =
= idB (f (a)) = (idB ◦ f )(a)

23. 4 EXEMPLOS DE CATEGORIAS 23
Definindo Top:
• Uma topologia em um conjunto A ´ uma cole¸ao
e c˜
β = {Aλ ⊆ A|λ ∈ L} de partes de A, chamados
abertos da topologia, tal que:
1. ∅, A ∈ β;
2. Se Aλ1 , . . . , Aλn ∈ β ent˜o ∩n Aλi ∈ β;
a i=1
3. Se {Aλ }λ∈V , com Aλ ∈ β para cada λ ∈ V e
V ⊆ L, ent˜o ∪λ∈V Aλ ∈ β;
a

24. 4 EXEMPLOS DE CATEGORIAS 24
• Um conjunto A com uma topologia β ´ um espa¸o
e c
topol´gico;
o
• Uma fun¸ao f : A → B ´ cont´nua em a ∈ A se para
c˜ e ı
todo aberto V de B tal que f (a) ∈ V existe um
aberto U de A tal que a ∈ U e f (U ) ⊆ V ;
• Se f : A → B ´ cont´
e ınua para todo a ∈ A ent˜o
a
dizemos que f ´ cont´nua;
e ı
• Observe-se que a composi¸˜o de fun¸˜es cont´
ca co ınuas ´
e
uma fun¸ao cont´
c˜ ınua.

25. 4 EXEMPLOS DE CATEGORIAS 25
Definindo Vect:
• Um espa¸o vetorial E ´ um conjunto, cujos elementos
c e
s˜o chamados vetores, no qual est˜o definidas duas
a a
opera¸˜es:
co
adi¸˜o u + v ∈ E para cada u, v ∈ E;
ca
multiplica¸˜o por escalar α.v, para cada α ∈ R e
ca
v ∈ E;
• Estas opera¸oes devem satisfazer as propriedades de
c˜
comutatividade, associatividade, existˆncia do vetor
e
nulo, existˆncia do inverso aditivo, e distributividade;
e

26. 4 EXEMPLOS DE CATEGORIAS 26
• Dados dois espa¸os vetoriais E e F, uma
c
transforma¸˜o linear A : E → F ´ uma
ca e
correspondˆncia que associa a cada vetor v ∈ E um
e
vetor A(v) ∈ F de modo que vale, para quaisquer
u, v ∈ E e α ∈ R:
1. A(u + v) = A(u) + A(v);
2. A(α.v) = α.A(v);
• Observe-se que a composi¸˜o de transforma¸˜es
ca co
lineares ´ associativa.
e

27. 4 EXEMPLOS DE CATEGORIAS 27
Definindo Grp:
• Um conjunto G com uma opera¸˜o ⊕ : G × G → G ´
ca e
um grupo se:
1. a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c, para todo a, b, c ∈ G;
2. Existe e ∈ G, chamado neutro, tal que
a ⊕ e = e ⊕ a = a, para todo a ∈ G;
3. Para todo a ∈ G existe a−1 ∈ G tal que
a ⊕ a−1 = a−1 ⊕ a = e;
• Exemplo: (Z, +) ´ um grupo;
e

28. 4 EXEMPLOS DE CATEGORIAS 28
• Uma fun¸˜o φ : G1 → G2 , onde G1 e G2 s˜o grupos, ´
ca a e
um homomorfismo de grupos se:
1. φ(eG1 ) = eG2 , onde eG1 ´ o neutro de G1 e eG2 ´ o
e e
neutro de G2 ;
2. φ(a ⊕G1 b) = φ(a) ⊕G2 φ(b), para todo a, b ∈ G1 ;
• Observe-se que a composi¸˜o de homomorfismos de
ca
grupos ´ associativa.
e

29. 4 EXEMPLOS DE CATEGORIAS 29
Definindo PO:
• Um conjunto parcialmente ordenado ´ um par (A, ),
e
onde A ´ um conjunto e ´ uma ordem parcial sobre
e e
o conjunto A;
• Uma fun¸ao f ´ monotˆnica se ela preserva a ordem,
c˜ e o
ou seja, x1 x2 ⇒ f (x1 ) f (x2 );
• Sabe-se que a composi¸ao de duas fun¸˜es
c˜ co
monotˆnicas ´ uma fun¸˜o monotˆnica.
o e ca o

30. 4 EXEMPLOS DE CATEGORIAS 30
Observa¸˜es e mais exemplos:
co
• A no¸ao de “categoria” considera objetos como
c˜
cole¸˜es de conjuntos estruturados e morfismos como
co
as suas fun¸oes associadas;
c˜
• N˜o devemos restringir nossas defini¸oes pois os
a c˜
morfismos n˜o necessariamente s˜o “fun¸˜es”, um
a a co
exemplo ´ a categoria Rel que possui conjuntos como
e
objetos e rela¸˜es como morfismos;
co

31. 4 EXEMPLOS DE CATEGORIAS 31
• Em Teoria das Categorias n˜o consideramos a
a
estrutura interna dos objetos, apenas as rela¸oes
c˜
estabelecidas entre eles pelos seus morfismos;
• Categoria Amor:

32. 4 EXEMPLOS DE CATEGORIAS 32
• A menor categoria poss´ ´ a categoria 1 que possui
ıvel e
apenas um objeto e uma seta (a identidade do
objeto);
• Uma categoria ´ chamada discreta se cada seta ´ a
e e
identidade de algum objeto;
• Esta categoria seria totalmente determinada pela
cole¸˜o de seus objetos;
ca
• Um exemplo de categoria discreta ´ a categoria 1;
e

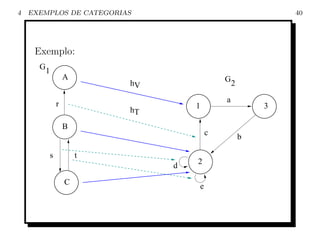
33. 4 EXEMPLOS DE CATEGORIAS 33
• Uma categoria ´ chamada de pr´-ordem se, para cada
e e
par de objetos a e b, existe no m´ximo um morfismo
a
f : a → b;
• Uma pr´-ordem ´ totalmente determinada pela
e e
rela¸˜o de pr´-ordem entre seus objetos;
ca e
• Em uma pr´-ordem, toda seta f : a → b pode ser
e
identificada pelo par (a, b);
• Assim, toda a informa¸ao sobre a categoria C, que ´
c˜ e
uma pr´-ordem, ´ dada pela rela¸˜o
e e ca
RC = {(a, b)|∃f ∈ C[a, b]};

34. 4 EXEMPLOS DE CATEGORIAS 34
• Toda categoria discreta ´ uma pr´-ordem;
e e
• A menor categoria n˜o-discreta que ´ uma pr´-ordem
a e e
´ a categoria 2, que possui dois objetos (chamaremos
e
de 0 e 1) e trˆs setas: as duas identidades e a seta
e
(0, 1) : 0 → 1;
id0 id1
Ö Ö
0 G1
(0,1)

35. 4 EXEMPLOS DE CATEGORIAS 35
• Um monoide ´ um conjunto tendo uma opera¸ao
e c˜
bin´ria associativa e um elemento neutro:
a
(A, ⊕, e)
Onde: A – conjunto suporte;
⊕ : A × A → A – opera¸˜o bin´ria;
ca a
e – elemento neutro, tal que
a ⊕ e = e ⊕ a = a, ∀a ∈ A;

36. 4 EXEMPLOS DE CATEGORIAS 36
• Podemos interpretar um monoide como uma
categoria que possui apenas um objeto, e a
composi¸˜o de morfismos seria a opera¸ao bin´ria;
ca c˜ a
• Exemplo: (N, +, 0), e o elemento neutro ´ o 0
e
(identidade):
1 2
0 5 Ò 3
∗ p™
€
... 4
5

37. 4 EXEMPLOS DE CATEGORIAS 37
• Sistemas dedutivos podem ser interpretados como
categorias;
• O morfismo f : a → b corresponde ` prova a
a b;
• Observe-se que a categoria ´ obtida na presen¸a da
e c
identidade ida : a → a, correspondente a prova trivial
a a, e da composi¸ao associativa de provas:
c˜
f :a→b g:b→c
.
g◦f :a→c

38. 4 EXEMPLOS DE CATEGORIAS 38
• Um grafo ´ uma qu´drupla G = (V, T, δ0 , δ1 ), tal que:
e a
V um conjunto de nodos ou v´rtices;
e
T um conjunto de arcos ou arestas;
δ0 , δ1 : T → V fun¸˜es totais denominadas origem e
co
destino;
• Categoria Gr: Possui como objetos todos os grafos e
como morfismos os homomorfismos de grafos;

39. 4 EXEMPLOS DE CATEGORIAS 39
• Sejam G1 = (V1 , T1 , δ01 , δ11 ) e G2 = (V2 , T2 , δ02 , δ12 ).
Um homomorfismo de grafos:
h : G1 → G2
´ um par de fun¸oes:
e c˜
h = (hV , hT )
onde: hV : V1 → V2 e hT : T1 → T2 s˜o tais que:
a
δ02 ◦ hT = hV ◦ δ01 e δ12 ◦ hT = hV ◦ δ11 .

40. 4 EXEMPLOS DE CATEGORIAS 40
Exemplo:
G
1
A G
hV 2
r a
hT 1 3
B
c b
s t
2
d
C e

41. 5 SUBCATEGORIA 41
5 Subcategoria
Uma categoria D ´ uma subcategoria de uma categoria C
e
se:
1. ObD ⊆ ObC ;
2. Para todo a e b em ObD , D[a, b] ⊆ C[a, b];
3. Composi¸oes e identidades em D coincidem com as
c˜
de C.

42. 5 SUBCATEGORIA 42
Uma subcategoria ´ completa se, para todo a e b em
e
ObD , D[a, b] = C[a, b]. Uma subcategoria completa ´
e
totalmente determinada pela cole¸ao de seus objetos.
c˜

43. 6 CATEGORIA DUAL 43
6 Categoria Dual
A categoria dual C op da categoria C tem os mesmos
objetos e os mesmos morfismos de C, idop = idb ,
b
domop (f ) = cod(f ), codop (f ) = dom(f ), e f ◦op g = g ◦ f .

44. 6 CATEGORIA DUAL 44
Observa¸˜es:
co
• C op [b, a] = C[a, b] e (C op )op = C;
• Se P ´ uma proposi¸ao que ´ verdadeira na categoria
e c˜ e
C, ent˜o P op ´ verdadeira em C op ;
a e
• Se P ´ uma proposi¸ao verdadeira para qualquer
e c˜
categoria, ent˜o P op tamb´m ´ verdadeira para
a e e
qualquer categoria, pois toda categoria ´ dual de sua
e
dual.

45. 6 CATEGORIA DUAL 45
Com rela¸ao ao diagrama da categoria dual:
c˜
• Para obter o diagrama da dual basta inverter as
setas;
• O diagrama da dual comuta se e somente se o
diagrama original comuta.

46. 7 CATEGORIA PRODUTO 46
7 Categoria Produto
Dadas duas categorias C e D, a categoria produto C × D
tem por objetos os pares (a, b), onde a e b s˜o os objetos
a
das categorias C e D respectivamente, e por morfismos os
pares (f, g) : (a, b) → (a , b ), onde f : a → a e g : b → b
s˜o morfismos de C e D respectivamente. Finalmente,
a
id(a,b) = (ida , idb ) e (f, g) ◦ (f , g ) = (f ◦ f , g ◦ g ).

47. 8 CATEGORIAS C ↓ A E C ↑ A 47
8 Categorias C ↓ a e C ↑ a
Dada uma categoria C e um objeto a ∈ ObC , a categoria
C ↓ a de objetos sobre a (tamb´m conhecida como
e
categoria fatia, “slice category”) ´ definida como:
e
1. ObC↓a = {f ∈ MorC |cod(f ) = a};
2. Dados dois objetos f : b → a e g : c → a, um
morfismo com origem f e destino g ´ uma seta
e
h ∈ C[b, c] tal que g ◦ h = f ;
3. Identidades e composi¸ao de C ↓ a s˜o herdadas de C.
c˜ a

48. 8 CATEGORIAS C ↓ A E C ↑ A 48
Em C:
b bb
bb f
bb
bb
1
h a
c
 
 g
c
Em C ↓ a:
h G [g : c → a]
[f : b → a]

49. 8 CATEGORIAS C ↓ A E C ↑ A 49
Em C:
b bb
bb f
bb
bb
0
idb a
ÐÐd
ÐÐÐ
ÐÐÐ f
b
Em C ↓ a:
idb
Ù
[f : b → a]

50. 8 CATEGORIAS C ↓ A E C ↑ A 50
• Considere Set ↓ A;
• Podemos pensar um objeto g : B → A desta
categoria como sendo uma fam´ de conjuntos
ılia
disjuntos indexados por A, {g −1 (a)}a∈A ;
• h : B → B ´ um morfismo de g : B → A para
e
g : B → A se e somente se
∀b b ∈ g −1 (a) ⇒ h(b) ∈ g −1 (a);

51. 8 CATEGORIAS C ↓ A E C ↑ A 51
Podemos definir tamb´m uma categoria C ↑ a, cujos
e
objetos s˜o os morfismos de C que tem como origem a.
a

52. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 52
9 Monomorfismo, Epimorfismo e
Isomorfismo
• Uma fun¸ao f : A → B ´ injetiva quando, para todo
c˜ e
a, a ∈ A, se f (a) = f (a ) ent˜o a = a ;
a
• Conclui-se que, para f injetiva, dadas duas fun¸oes
c˜
g : C → A e h : C → A, se para todo c ∈ C
f (g(c)) = f (h(c)) ent˜o para todo c ∈ C g(c) = h(c),
a
ou seja, f ◦ g = f ◦ h implica g = h;
• O inverso tamb´m ´ verdade, ou seja, se f ◦ g = f ◦ h
e e
implica g = h ent˜o f ´ injetiva;
a e

53. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 53
• Suponha o contr´rio, ent˜o existem a e a tal que
a a
f (a) = f (a ) mas a = a ;
• Definimos g tal que g(c) = a para todo c ∈ C e h tal
que h(c) = a para todo c ∈ C;
• Ent˜o, f ◦ g = f ◦ h mas g = h, o que ´ uma
a e
contradi¸ao;
c˜

54. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 54
• f ◦ g = f ◦ h implica g = h se e somente se f ´e
injetiva (como se a aplica¸˜o de f se cancelasse a
ca
esquerda);
• De forma similar, g ◦ f = h ◦ f implica g = h se e
somente se f ´ sobrejetiva (como se a aplica¸ao de f
e c˜
se cancelasse a direita).

55. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 55
Sejam uma categoria C e a, b ∈ ObC . Ent˜o:
a
1. Uma seta h ∈ C[a, b] ´ um monomorfismo (ou ´
e e
mono) se e somente se h ◦ g = h ◦ f ⇒ g = f ;
2. Uma seta h ∈ C[a, b] ´ um epimorfismo (ou ´ epi ) se
e e
e somente se g ◦ h = f ◦ h ⇒ g = f ;
3. Uma seta h ∈ C[a, b] ´ um isomorfismo (ou ´ iso) se e
e e
somente se existe g ∈ C[b, a] tal que g ◦ h = id e
h ◦ g = id.

56. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 56
h◦g=h◦f
g '
G h G b ent˜o g = f ;
Mono c Ga a
f
g◦h=f ◦h
g 'G
h Gb
Epi a G c ent˜o g = f ;
a
f
id id
Ó h G Ó
Iso a o b e g ◦ h = id e h ◦ g = id.
g

57. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 57
Observa¸˜es:
co
• Se uma seta h ´ iso, ent˜o tamb´m ´ epi e mono,
e a e e
embora o contr´rio n˜o seja necessariamente
a a
verdadeiro:
Se h ´ iso, ent˜o existe f tal que f ◦ h = id. Logo,
e a
h◦g =h◦g ⇒f ◦h◦g =f ◦h◦g ⇒g =g. O
argumento ´ similar para epi.
e
• Embora seja util em Set pensar mono e epi como
´
sendo inje¸ao e sobreje¸ao respectivamente, isto pode
c˜ c˜
conduzir a confus˜o em outras categorias;
a

58. 9 MONOMORFISMO, EPIMORFISMO E ISOMORFISMO 58
• Um mono h ∈ C[a, b] cinde (“split”) se existe um
g ∈ C[b, a] tal que g ◦ h = ida ;
• Um epi h ∈ C[a, b] cinde (“split”) se existe um
g ∈ C[b, a] tal que h ◦ g = idb .

59. 10 ´
OBJETOS ISOMORFICOS 59
10 Objetos Isom´rficos
o
• Dois objetos a e b s˜o isom´rficos (a ∼ b) se existe
a o =
um isomorfismo h ∈ C[a, b];
• Isomorfismo estabelece, em certo grau de abstra¸ao,
c˜
uma rela¸˜o de “semelhan¸a” ou “equivalˆncia” entre
ca c e
objetos.

60. 11 MORFISMO PRINCIPAL 60
11 Morfismo Principal
Seja C uma categoria e a, b ∈ ObC . Ent˜o:
a
1. Uma seta h ∈ C[a, b] ´ um morfismo principal se e
e
somente se ∀f ∈ C[a, b] ∃g ∈ C[a, a] f = h ◦ g;
2. Um par de setas f ∈ C[a, b] e g ∈ C[b, a] ´ um par de
e
retra¸˜o se e somente se g ◦ f = id. Ent˜o a ´
ca a e
chamado de retra¸˜o de b (a b) via o par de
ca
retra¸˜o (f, g).
ca

61. 11 MORFISMO PRINCIPAL 61
Observa¸˜es:
co
• h ´ principal se e somente se para todo f existe um g
e
tal que:
h Gb
a
y d
ÐÐÐ
g
ÐÐÐf
ÐÐ
a
• f e g s˜o um par de retra¸˜o (a b) se:
a ca
f g
a Gb Ga
e g ◦ f = id.

62. 11 MORFISMO PRINCIPAL 62
Teorema 1 Sejam C uma categoria e a, b ∈ ObC . Ent˜o:
a
1. Se a b via (i, h), ent˜o h ´ epi e principal, e i ´
a e e
mono;
2. Se h ∈ C[a, b] ´ principal e existe um epi k ∈ C[a, b],
e
ent˜o h ´ epi;
a e
3. Se a b e f ∈ C[b, a] ´ principal, ent˜o existe
e a
g ∈ C[a, b] tal que a b via (g, f ).

63. 11 MORFISMO PRINCIPAL 63
Prova:
1. Se a b via (i, h), ent˜o h ´ epi e principal, e i ´
a e e
mono;
• g ◦ h = f ◦ h ⇒ g ◦ h ◦ i = f ◦ h ◦ i ⇒ g = f para
h ◦ i = id;
• Prova que h ´ principal: ∀f ∃g f = h ◦ g. Tome
e
g = i ◦ f , ent˜o h ◦ g = h ◦ i ◦ f = f . Segundo o
a
diagrama:
a i Gb
y
f h
b Ga
f
• i ◦ g = i ◦ f ⇒ h ◦ i ◦ g = h ◦ i ◦ f ⇒ g = f;

64. 11 MORFISMO PRINCIPAL 64
2. Se h ∈ C[a, b] ´ principal e existe um epi k ∈ C[a, b],
e
ent˜o h ´ epi;
a e
g◦h=f ◦h⇒g◦h◦g =f ◦h◦g ⇒g◦k =
f ◦ k ⇒ g = f (para um g apropriado);
h Gb
a
y
ÐÐd
g ÐÐÐ
ÐÐÐ k
a

65. 11 MORFISMO PRINCIPAL 65
3. Se a b e f ∈ C[b, a] ´ principal, ent˜o existe
e a
g ∈ C[a, b] tal que a b via (g, f );
Seja a b via (i, j). Como f ´ principal ent˜o
e a
∃s ∈ C[b, b] j = f ◦ s. Assim, para g = s ◦ i temos
f ◦ g = j ◦ i = ida . Em diagrama:
i j
aa Gb Ga
aa d
aa ÑÑÑ
g aa s ÑÑÑ
a0 ÑÑ f
b

66. 12 CATEGORIA DOS IDEMPOTENTES 66
12 Categoria dos Idempotentes
Se f : a → b e g : b → a s˜o um par de retra¸˜o, ent˜o a
a ca a
fun¸ao h = f ◦ g : b → b ´ idempotente, isto ´, h ◦ h = h,
c˜ e e
pois h ◦ h = (f ◦ g) ◦ (f ◦ g) = f ◦ (g ◦ f ) ◦ g = f ◦ g = h
(pela associatividade da composi¸˜o).
ca

67. 12 CATEGORIA DOS IDEMPOTENTES 67
Dada uma categoria C e um objeto b ∈ ObC , a categoria
dos idempotentes sobre b (Retb ) ´ definida como:
e
ObRetb = {f ∈ C[b, b]|f ◦ f = f }
MorRetb = {(f, k, g)|f, g ∈ ObRetb , k ∈ C[b, b],
k = g ◦ k ◦ f}
dom((f, k, g)) = f
cod((f, k, g)) = g
idf = (f, f, f )
(f, k, g) ◦ (g , k , f ) = (g , k ◦ k , g)

68. 12 CATEGORIA DOS IDEMPOTENTES 68
identidade (f, k, g) ◦ (f, f, f ) = (f, k ◦ f, g). Sabemos
que f e g s˜o idempotentes e k = g ◦ k ◦ f :
a
k◦f =g◦k◦f ◦f =g◦k◦f =k
Similar para (f, f, f ) ◦ (g, k, f );
associatividade da composi¸˜o ca
((f1 , f2 , f3 ) ◦ (g1 , g2 , f1 )) ◦ (h1 , h2 , g1 ) =
(g1 , f2 ◦ g2 , f3 ) ◦ (h1 , h2 , g1 ) = (h1 , (f2 ◦ g2 ) ◦ h2 , f3 ) =
(h1 , f2 ◦ (g2 ◦ h2 ), f3 ) e
(f1 , f2 , f3 ) ◦ ((g1 , g2 , f1 ) ◦ (h1 , h2 , g1 )) =
(f1 , f2 , f3 ) ◦ (h1 , g2 ◦ h2 , f1 ) = (h1 , f2 ◦ (g2 ◦ h2 ), f3 ).

69. 13 SUB-OBJETO 69
13 Sub-objeto
• Sub-objeto ´ a vers˜o categorial de subconjunto da
e a
teoria dos conjuntos;
• Baseia-se na id´ia de definir um subconjunto A ⊆ B
e
como um monomorfismo f : D → B (intuitivamente
“f (D) = A”);

70. 13 SUB-OBJETO 70
• Se existem muitas setas mono definindo o mesmo
subconjunto, ´ necess´rio introduzir uma classe de
e a
equivalˆncia e definir sub-objetos usando-a;
e
• Seja C uma categoria. Se f : b → a e g : c → a s˜o
a
duas setas mono com destino comum a, ent˜o a
dizemos que f ≤ g se e somente se existe h : b → c
tal que g ◦ h = f ;
• Note que o unico h ´ mono tamb´m, pois
´ e e
h◦k =h◦k ⇒g◦h◦k =g◦h◦k ⇒f ◦k =
f ◦k ⇒k =k;

71. 13 SUB-OBJETO 71
• Se f ≤ g e g ≤ f ent˜o dizemos que f ∼ g, e ∼ ´
a = =e
uma rela¸ao de equivalˆncia entre monomorfismos
c˜ e
com destino comum;
• As classes de equivalˆncia determinadas por esta
e
rela¸˜o de equivalˆncia s˜o os sub-objetos de a;
ca e a
• Nota¸˜o: [f ].
ca

72. 14 OBJETOS INICIAL E TERMINAL 72
14 Objetos Inicial e Terminal
Seja C uma categoria. Um objeto 0 ´ inicial se e somente
e
se para qualquer b ∈ ObC existe um unico f ∈ C[0, b].
´

73. 14 OBJETOS INICIAL E TERMINAL 73
Observa¸˜es:
co
• O t´
ıpico exemplo de objeto inicial ´ ∅ (conjunto
e
vazio) em Set, pois a fun¸ao vazia (ou seja, a fun¸˜o
c˜ ca
cujo grafo ´ vazio) ´ a unica seta com origem em ∅;
e e ´
• Deve-se observar que a fun¸˜o vazia, tendo como
ca
dom´
ınio ∅, ´ total (como Set exige) por vacuidade;
e
• Inicialidade ´ a mais simples no¸ao universal em
e c˜
Teoria das Categorias, j´ que ´ dada pela existˆncia e
a e e
unicidade de morfismos satisfazendo certas
propriedades;
• Universalidade ´ um conceito fundamental em Teoria
e
das Categorias.

74. 14 OBJETOS INICIAL E TERMINAL 74
Teorema 2 Se 0 e 0 s˜o dois objetos iniciais da
a
categoria C, ent˜o eles s˜o isom´rficos (em outras
a a o
palavras: o objeto inicial ´ unico a n˜o ser por
e´ a
isomorfismos).
Prova: Sejam i : 0 → 0 e j : 0 → 0 dois morfismos
dados pela inicialidade de 0 e 0 . Ent˜o, j ◦ i : 0 → 0,
a
mas tamb´m id0 : 0 → 0. Pela inicialidade de 0 s´ pode
e o
existir um morfismo em C[0, 0], ent˜o j ◦ i = id0 . Da
a
mesma forma, pela inicialidade de 0 , i ◦ j = id0 .

75. 14 OBJETOS INICIAL E TERMINAL 75
• Podemos usar dualidade para definir um novo
conceito e provar novas propriedades;
• Seja P (c) a propriedade “para qualquer b ∈ ObC
existe um unico f tal que dom(f ) = c e cod(f ) = b”;
´
• Pela defini¸˜o, c ´ inicial se e somente se P (c) vale;
ca e
• O enunciado dual de P (c), P op (c), ´ “para qualquer
e
b ∈ ObC existe um unico f tal que dom(f ) = b e
´
cod(f ) = c”;

76. 14 OBJETOS INICIAL E TERMINAL 76
• Conceitos duais s˜o usualmente chamados usando-se
a
o prefixo “co-”;
• Assim, P op (c) define co-inicialidade, e o objeto que a
satisfaz ´ o objeto co-inicial (tamb´m conhecido
e e
como terminal );
• Nota¸˜o: 1 ou t e o morfismo unico que tem como
ca ´
origem um objeto a e como destino t ´ denotado por
e
!a : a → t.

77. 14 OBJETOS INICIAL E TERMINAL 77
Observa¸˜es:
co
• Qualquer conjunto unit´rio {∗} (que possui apenas
a
um elemento) ´ terminal em Set;
e
• Na categoria 2 um elemento ´ inicial e o outro ´
e e
terminal;
• Se c ´ inicial em C ent˜o ´ terminal em C op e
e a e
vice-versa.

78. 14 OBJETOS INICIAL E TERMINAL 78
Teorema 3 Se 1 e 1 s˜o dois objetos terminais na
a
categoria C, ent˜o eles s˜o isom´rficos.
a a o
Prova: Pela dualidade e pelo Teorema 2.

79. 14 OBJETOS INICIAL E TERMINAL 79
Observa¸˜es:
co
• Um objeto pode ser inicial e terminal ao mesmo
tempo, neste caso ´ chamado de objeto zero;
e
• Em Set, um morfismo do conjunto unit´rio para um
a
conjunto A define os elementos de A;
• Em uma categoria C qualquer, uma seta de um
objeto terminal t para um objeto a ´ usualmente
e
chamada de elemento ou ponto de a;

80. 14 OBJETOS INICIAL E TERMINAL 80
• Seja C uma categoria. t ∈ ObC ´ um gerador se e
e
somente se para todos a, b ∈ ObC e todos
f, g ∈ C[a, b], temos
f = g ⇒ ∃h ∈ C[t, a] f ◦ h = g ◦ h;
• C tem suficientes pontos (ou ´ bem pontuada), se
e
existe um gerador t que ´ terminal na categoria dada;
e
• Ou seja, a categoria tem suficientes pontos quando as
setas com origem no objeto terminal permitem
discriminar entre morfismos, de forma similar que
para os elementos de Set.

81. 15 PRODUTO E COPRODUTO CATEGORIAL 81
15 Produto e Coproduto
Categorial
• O produto categorial ´ uma generaliza¸ao estrutural
e c˜
da no¸ao de produto cartesiano;
c˜
• Dados dois conjuntos A e B, seu produto cartesiano
´:
e
A × B = {(x, y)|x ∈ A, y ∈ B}

82. 15 PRODUTO E COPRODUTO CATEGORIAL 82
• Associado com este conjunto existem dois
mapeamentos especiais pA : A × B → A e
pB : A × B → B, chamados proje¸˜es, tal que para
co
todo (x, y) ∈ A × B, pA ((x, y)) = x e pB ((x, y)) = y;
• Sejam f : C → A e g : C → B, ent˜o
a
f, g : C → A × B, e f, g (c) = f (c), g(c)
para todo c ∈ C;
• Seja c ∈ ObC . Definimos a opera¸ao c˜
, c : C[c, a] × C[c, b] → C[c, a × b] como acima
descrito.

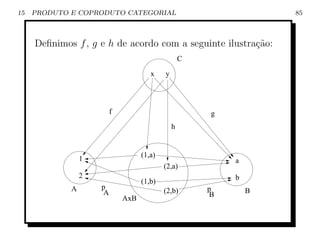
83. 15 PRODUTO E COPRODUTO CATEGORIAL 83
Sejam C uma categoria e a, b ∈ ObC . O produto categorial
de a e b ´ um objeto a × b junto com dois morfismos
e
pa : a × b → a e pb : a × b → b tal que, dado um c ∈ ObC ,
para qualquer f ∈ C[c, a] e g ∈ C[c, b], existe exatamente
um h ∈ C[c, a × b] tal que o seguinte diagrama ´ e
comutativo:
c
y ii
y ii g
f yy ii
yy h ii
|oyyy i4
a pa a × b pb G b
Observa¸˜o: c ´ chamado de pr´-produto.
ca e e

84. 15 PRODUTO E COPRODUTO CATEGORIAL 84
Exemplos: Em Set, sejam A = {1, 2}, B = {a, b} e
C = {x, y}. Ent˜o A × B = {(1, a), (2, a), (1, b), (2, b)} e h
a
´ o unico morfismo que faz o seguinte diagrama comutar:
e ´
w C qqq
f www qqg
w h qq
ww qq
{ww 5
A pA A × B pB G B
o

85. 15 PRODUTO E COPRODUTO CATEGORIAL 85
Definimos f , g e h de acordo com a seguinte ilustra¸ao:
c˜
C
x y
f g
h
1 (1,a)
a
(2,a)
2 b
(1,b)
A p (2,b) p B
A B
AxB

86. 15 PRODUTO E COPRODUTO CATEGORIAL 86
Na categoria 2,
id0 id1
Ö Ö
0 G1
(0,1)
0 × 1 = 1 × 0 = 0:
z 0 iii
id0 zzz i (0,1)
zz id0 iii
zz ii
|z
o 4G
0 id0
0 × 1 (0,1) 1

87. 15 PRODUTO E COPRODUTO CATEGORIAL 87
Em Set, ∅ × A = A × ∅ = ∅:
z ∅ iii
id∅ zzz ii f
zz id∅ iii
z ii
| zz 4
∅ oz ∅×A G A
id∅ f

88. 15 PRODUTO E COPRODUTO CATEGORIAL 88
Teorema 4 Em uma categoria, o produto, se existir, ´
e
unico a n˜o ser por isomorfismos.
´ a
Prova: Seja a ⊗ b um produto alternativo com proje¸˜esco
qa e qb , ent˜o qa , qb ◦ pa , pb ´ o morfismo unico
a e ´
que faz o seguinte diagrama comutar:
a×b
g
zz g p
pa zp ,p ggg b
z a b
zz gg
z gg
}zz qa
o
a —hh a⊗b
qb
Ga3 b
{
hh
hh q ,q {{ {{
pa h h a b {{{ pb
h
{
a×b
Logo, qa , qb ◦ pa , pb = ida×b e, por simetria,
pa , pb ◦ qa , qb = ida⊗b .

89. 15 PRODUTO E COPRODUTO CATEGORIAL 89
Morfismo produto: Sejam f : a → c e g : b → d.
pa pb
ao a×b Gb
f f ×g g
co pc c×d pd
Gd
Observa¸˜es:
co
• f × g ´ unico j´ que a × b ´ um pr´-produto de c × d;
e´ a e e
• Dizemos que f × g ´ univocamente induzido por f e
e
g;
• Exemplo em Set: Definimos
(f × g)((x, y)) = (f (x), g(y)) tal que x ∈ A e y ∈ B.

90. 15 PRODUTO E COPRODUTO CATEGORIAL 90
• Uma categoria C ´ cartesiana (C ´ CC) se e somente
e e
se:
1. Cont´m um objeto terminal t;
e
2. Todo par a, b ∈ ObC tem um produto categorial
(a × b, pa,b,1 : a × b → a, pa,b,2 : a × b → b);
• Exemplos: Set, Top e Grp;
• Uma categoria cartesiana interessante em teoria da
computabilidade ´ a categoria EN dos conjuntos
e
enumer´veis;
a

91. 15 PRODUTO E COPRODUTO CATEGORIAL 91
• Objetos de EN s˜o pares a = (a, ea ), onde a ´ um
a e
conjunto cont´vel e ea : N → a ´ um mapeamento
a e
dos elementos de a (uma enumera¸˜o de a);
ca
• f ∈ EN[a, b] se e somente se, para alguma fun¸ao
c˜
(total) recursiva f , o seguinte diagrama comuta:
f
N GN
ea eb
a Gb
f
• Dizemos que f representa f ;

92. 15 PRODUTO E COPRODUTO CATEGORIAL 92
• O produto pode ser facilmente obtido por qualquer
bije¸˜o efetiva [, ] : N × N → N;
ca
• Um conjunto enumer´vel de interesse ´
a e
PR = (PR, φ), das fun¸˜es parciais recursivas com
co
n´meros de G¨del φ : N → PR, e EN[PR, PR] s˜o
u o a
exatamente os funcionais recursivos de segunda
ordem.

93. 15 PRODUTO E COPRODUTO CATEGORIAL 93
Sejam C uma categoria e a, b ∈ ObC . O coproduto de a e b
´ um objeto a + b junto com dois morfismos
e
qa : a → a + b e qb : b → a + b tal que, dado um c ∈ ObC ,
para qualquer f ∈ C[a, b] e g ∈ C[b, c], existe exatamente
um h ∈ C[a + b, c] tal que o seguinte diagrama comuta:
c
y` y ˜iii
f yyy iig
y ii
yy h
ii
yy G o
a qa a+b qb b

94. 15 PRODUTO E COPRODUTO CATEGORIAL 94
Observa¸˜es:
co
• O coproduto ´ o conceito dual do produto;
e
• No coproduto a + b, os morfismos qa e qb s˜o
a
chamados de inclus˜es ;
o
• Por dualidade, o coproduto ´ unico (a n˜o ser por
e´ a
isomorfismos);
• Em Set o coproduto ´ a uni˜o disjunta.
e a

95. 16 ´
CALCULO LAMBDA 95
16 C´lculo Lambda
a
• Simplifica e flexibiliza a representa¸ao de fun¸oes;
c˜ c˜
• Facilita as opera¸oes de currying e uncurrying.
c˜

96. 16 ´
CALCULO LAMBDA 96
Express˜o-λ (ou termo-λ):
a
1. Uma vari´vel ´ uma express˜o-λ;
a e a
2. Se M ´ uma express˜o-λ e x ´ uma vari´vel, ent˜o
e a e a a
λxM ´ uma express˜o-lambda, interpretada como
e a
“uma fun¸ao com argumento x”;
c˜
3. Se F e A s˜o express˜es-λ, ent˜o (F A) ´ uma
a o a e
express˜o-λ, interpretada como “F aplicado ao
a
argumento A”;
4. Nada mais ´ express˜o-λ.
e a

97. 16 ´
CALCULO LAMBDA 97
Exemplos:
M
1. λx x ;
F
2. ( λxx (yz));
A
F A
3. (λx (xx) y );
M
4. (λxx λxx );
F A
5. λx λy(xy).
M

98. 16 ´
CALCULO LAMBDA 98
Ocorrˆncia de vari´vel livre e limitada:
e a
• Se uma ocorrˆncia de uma vari´vel x est´ no escopo
e a a
de um λx, ent˜o sua ocorrˆncia ´ dita limitada, caso
a e e
contr´rio ´ dita livre;
a e
• Exemplo:
(xλxλy(xy))
Primeira ocorrˆncia de x ´ livre, a segunda ´
e e e
limitada.

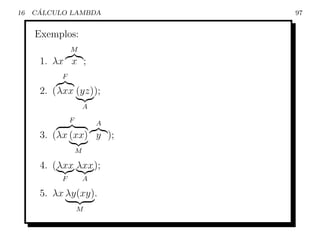
99. 16 ´
CALCULO LAMBDA 99
Substitui¸˜o uniforme:
ca
• M [x ← A] denota a substitui¸ao uniforme de todas
c˜
as ocorrˆncias livres de x por A;
e
• Exemplo:
(xλxλy(xy))[x ← λzz] = (λzzλxλy(xy))

100. 16 ´
CALCULO LAMBDA 100
Abstra¸˜o-λ M ⇒ λxM ;
ca
Aplica¸˜o-λ (λxM A) ⇒ M [x ← A].
ca
(λxM A) ⇒ M [x ← A]
redex contractum

101. 16 ´
CALCULO LAMBDA 101
• Uma forma normal ´ uma express˜o-λ na qual n˜o se
e a a
pode efetuar uma aplica¸ao-λ;
c˜
• Uma sequˆncia de aplica¸oes-λ at´ a obten¸˜o de
e c˜ e ca
uma forma normal ´ chamada de redu¸˜o.
e ca

102. 16 ´
CALCULO LAMBDA 102
Exemplos de redu¸˜es:
co
1. (λxxλxx) ⇒ λxx;
2. ((λxλy(xy)λxx)x) ⇒ (λy(λxxy)x) ⇒ (λxxx) ⇒ x;
3. (λx(xx)λx(xx)) ⇒ (λx(xx)λx(xx)) (irredut´
ıvel);
4. (λxyz) ⇒ y (jogar fora alguma coisa).

103. 16 ´
CALCULO LAMBDA 103
Currying:
• Ocorre quando da aplica¸˜o de um termo-λ em que
ca
existem menos argumentos que vari´veis limitadas;
a
(λxλy(xy)z) ⇒ λy(zy)
• Ou seja, f (x, y), fixando um x qualquer, resulta em
uma fun¸ao de y.
c˜

104. 16 ´
CALCULO LAMBDA 104
Representando aritm´tica:
e
if A then B else C
T ≡ λxλyx
((T a)b) ≡ ((λxλyxa)b) ⇒ (λyab) ⇒ a
F ≡ λxλyy
((F a)b) ≡ ((λxλyya)b) ⇒ (λyyb) ⇒ b
Observa¸˜o: T e F s˜o abreviaturas.
ca a

105. 16 ´
CALCULO LAMBDA 105
Podemos usar F e T como seletores de elementos de
listas (if-then-else aninhados):
• T ≡ λxλyx (primeiro elemento da lista);
• F T ≡ λxλy(yλxλyx) ≡ λxλy(yT ) (segundo elemento
da lista);
• F 2 T ≡ λxλy(yλxλy(yλxλyx)) ≡ λxλy(yF T )
(terceiro elemento da lista);
• F i+1 T ≡ λxλy(yF i T ) (o (i + 2)-´simo elemento).
e

106. 16 ´
CALCULO LAMBDA 106
φ0 , φ1 , . . . , φn−1
• φ0 ≡ λx((xφ0 )ψ) (ψ ´ o terminador de lista);
e
• φ0 , φ1 ≡ λx((xφ0 )λx((xφ1 )ψ)) ≡ λx((xφ0 ) φ1 );
• φ0 , φ1 , . . . , φn−1 ≡ λx((xφ0 ) φ1 , . . . , φn−1 ).

107. 16 ´
CALCULO LAMBDA 107
Obtendo o primeiro elemento de uma lista:
( φ0 T ) ≡ (λx((xφ0 )ψ)λxλyx) ⇒ ((λxλyxφ0 )ψ) ⇒
⇒ (λyφ0 ψ) ⇒ φ0

108. 16 ´
CALCULO LAMBDA 108
Obtendo o segundo elemento de uma lista:
( φ0 , φ 1 , φ 2 F T ) ≡
≡ (λx((xφ0 )λx((xφ1 )λx((xφ2 )ψ))) λxλy(yλxλyx)) ⇒
⇒ ((λxλy(yλxλyx) φ0 )λx((xφ1 )λx((xφ2 )ψ))) ⇒
⇒ (λy(yλxλyx) λx((xφ1 )λx((xφ2 )ψ))) ⇒
⇒ (λx((xφ1 )λx((xφ2 )ψ)) λxλyx) ⇒
⇒ ((λxλyx φ1 )λx((xφ2 )ψ)) ⇒
⇒ (λyφ1 λx((xφ2 )ψ)) ⇒ φ1

109. 16 ´
CALCULO LAMBDA 109
Representando n´meros: 0 ≡ T , 1 ≡ F T , 2 ≡ F F T , . . .,
u
i ≡ F iT .

110. 16 ´
CALCULO LAMBDA 110
suc ≡ λzλxλy(yz)
(suc1) ≡ (λzλxλy(yz)λxλy(yλxλyx)) ⇒
λxλy(y λxλy(y λxλyx) ≡ F F T ≡ 2
T
FT

111. 16 ´
CALCULO LAMBDA 111
Observa¸˜es:
co
• Esta defini¸ao conduz a possibilidade de definir
c˜
soma, subtra¸ao, multiplica¸ao, etc.
c˜ c˜
• Neste caso, podemos definir abreviaturas para +, −,
×, etc.
• Assim, ocorre equivalˆncia entre o c´lculo-λ e a
e a
m´quina de Turing (fun¸˜es parciais recursivas).
a co

112. 16 ´
CALCULO LAMBDA 112
C´lculo-λ tipado:
a
• Cada vari´vel tem um tipo associado e a constru¸ao
a c˜
dos termos obedece a certas “regras de tipagem”;
• Motiva¸ao: Paradoxo de Russel (teoria dos
c˜
conjuntos) e tipos de linguagens de programa¸ao.
c˜

113. 16 ´
CALCULO LAMBDA 113
Tipos e construtores de termos:
Tipos atˆmicos A, B, C, . . .;
o
Tipos n˜o-atˆmicos
a o
• se α e β s˜o tipos, ent˜o α → β ´ um tipo
a a e
(funcional);
• se α e β s˜o tipos, ent˜o α × β ´ um tipo
a a e
(produto cartesiano, record);

114. 16 ´
CALCULO LAMBDA 114
Termos
• se x ´ vari´vel do tipo ψ, ent˜o x : ψ ´ um termo
e a a e
do tipo ψ;
• se x ´ vari´vel do tipo ψ e t ´ termo do tipo φ,
e a e
ent˜o λxt : ψ → φ ´ um termo do tipo ψ → φ;
a e
• se t1 e t2 s˜o termos do tipo ψ → φ e ψ
a
respectivamente, ent˜o App(t1 , t2 ) : φ ´ um termo
a e
do tipo φ (aplica¸ao);
c˜

115. 16 ´
CALCULO LAMBDA 115
• se t1 e t2 s˜o termos do tipo ψ e φ
a
respectivamente, ent˜o (t1 , t2 ) : ψ × φ ´ um
a e
termo do tipo ψ × φ (produto cartesiano);
• se t : ψ × φ ´ um termo do tipo ψ × φ, ent˜o
e a
π1 (t) : ψ e π2 (t) : φ s˜o termos do tipo ψ e φ
a
respectivamente (proje¸oes).
c˜

116. 16 ´
CALCULO LAMBDA 116
Redu¸oes no c´lculo-λ tipado:
c˜ a
π1 ((t1 , t2 )) : ψ ⇒ t1 : ψ
π2 ((t1 , t2 )) : φ ⇒ t2 : φ
App(λxt1 , t2 ) : φ ⇒ t1 [x ← t2 ] : φ

117. 16 ´
CALCULO LAMBDA 117
Observa¸˜es:
co
• O c´lculo-λ tipado corresponde `s fun¸oes (totais)
a a c˜
recursivas, pois a introdu¸˜o dos tipos impede que a
ca
fun¸˜o fique indefinida (n˜o h´ loop infinito);
ca a a
• Ao representar o c´lculo-λ tipado em Teoria das
a
Categorias:
– Tipos s˜o objetos de uma categoria C;
a
– Termos s˜o morfismos;
a
– Problema: como representar a aplica¸ao-λ?
c˜
Resposta: objeto exponencial.

118. 17 OBJETO EXPONENCIAL 118
17 Objeto Exponencial
• A conex˜o entre Teoria das Categorias e Teoria da
a
Computabilidade, como “teorias de fun¸oes”, exige
c˜
interpretar fun¸˜es como morfismos, identificando
co
tipos como A × B → C e A → (B → C) (currying e
uncurrying);
• O produto n˜o ´ suficiente para isto;
a e
• Precisamos ent˜o representar fun¸˜es de mais alta
a co
ordem (funcionais), como “morfismos entre
morfismos”, mas isto n˜o ´ poss´
a e ıvel;

119. 17 OBJETO EXPONENCIAL 119
Sejam C uma categoria cartesiana, e a, b ∈ ObC . O objeto
exponencial de a e b ´ ba junto com o morfismo
e
evala,b : ba × a → b (mapeamento de avalia¸ao), e para
c˜
cada objeto c uma opera¸ao Λc : C[c × a, b] → C[c, ba ] tal
c˜
que, para todos os morfismosf : c × a → b e h : c → ba , as
seguintes equa¸oes valem:
c˜
1. evala,b ◦ (Λc (f ) × ida ) = f ;
2. Λc (evala,b ◦ (h × ida )) = h.

120. 17 OBJETO EXPONENCIAL 120
Os conceitos centrais da defini¸ao s˜o:
c˜ a
Currying/Uncurrying f : c × a → b intercambiado
com h : c → ba , onde ba ´ o espa¸o de fun¸oes a → b;
e c c˜
Existˆncia de eval evala,b : ba × a → b equivale a
e
avaliar f (x), onde f : a → b e x ∈ a.

121. 17 OBJETO EXPONENCIAL 121
Observa¸˜es:
co
• Λ : C[c × a, b] → C[c, ba ] ´ uma bije¸˜o;
e ca
• Λ−1 : C[c, ba ] → C[c × a, b] ´ tal que
e
Λ−1 : h → evala,b ◦ (h × ida );
• Se Λ : C[c × a, b] → C[c, ba ] ´ uma bije¸ao e (1) da
e c˜
defini¸˜o vale, ent˜o (2) ´ necessariamente
ca a e
verdadeiro;
• Seja h ∈ C[c, ba ] e tomemos f ∈ C[c × a, b] tal que
h = Λ(f ), ent˜o Λ(evala,b ◦ (h × ida )) =
a
Λ(evala,b ◦ (Λ(f ) × ida )) = Λ(f ) = h.

122. 17 OBJETO EXPONENCIAL 122
Defini¸ao alternativa: Sejam C uma categoria cartesiana
c˜
e a, b ∈ ObC . O objeto exponencial de a para b ´ um
e
objeto ba junto com um morfismo evala,b : ba × a → b, tal
que para todos os morfismos f : c × a → b, existe um e
somente um h : c → ba tal que o seguinte diagrama
comuta:
f
c c×a G` b
y
yyy
h h×id yyy
yy evala,b
ba ba × a

123. 17 OBJETO EXPONENCIAL 123
Observa¸˜es:
co
• A defini¸ao de objeto exponencial sugere que ba
c˜
“representa” C[a, b];
• C[t, ba ] ∼ C[t × a, b] ∼ C[a, b];
= =
• Em Set, podemos dizer que a cardinalidade de B A ´
e
mn , onde m ´ a cardinalidade de B e n ´ a
e e
cardinalidade de A. Por exemplo, se A = ∅ ent˜o
a
n = 0 e mn = 1. O que resulta no morfismo unico h
´
h G A
em C B , j´ que, neste caso, B A ´ objeto
a e
terminal;

124. 17 OBJETO EXPONENCIAL 124
• Em Set o objeto exponencial de A e B ´ o conjunto
e
das f tal que f ´ fun¸˜o de A para B;
e ca
• B A = Set[A, B];
• eval : B A × A → B ´ dado pela regra
e
eval((f, x)) = f (x);
• Λ : Set[C × A, B] → Set[C, B A ] leva cada fun¸ao
c˜
f : C × A → B na fun¸ao Λ(f ) : C → B A definida
c˜
por Λ(f )(c) = λaf (c, a), onde
λaf (c, a) ∈ B A = Set[A, B] ´ a fun¸˜o que leva
e ca
a ∈ A para f (c, a) ∈ B;

125. 17 OBJETO EXPONENCIAL 125
• Observe-se que se a b via (i, j) ent˜o a retra¸ao ´
a c˜ e
um sub-objeto de b;
• Podemos estar interessados em categorias em que
vale aa a, mas isto ´ imposs´ em Set pelo
e ıvel
Teorema de Cantor, j´ que a cardinalidade de aa ´
a e
maior que a de a, desde que a = {∗}.

126. 17 OBJETO EXPONENCIAL 126
Rela¸ao com Teoria da Computabilidade:
c˜
• Seja {φi }i∈N = PR uma enumera¸˜o de G¨del
ca o
aceit´vel das fun¸˜es parciais recursivas. Ou seja,
a co
dada uma fun¸ao parcial recursiva f qualquer, ent˜o
c˜ a
existe um i tal que φi = f ;
• Seja [, ] : N × N → N uma bije¸ao efetiva;
c˜
• Defina f : N × N → N uma fun¸˜o bin´ria parcial
ca a
recursiva se e somente se
∃f ∈ PR f (x, y) = f ([x, y]);

127. 17 OBJETO EXPONENCIAL 127
• Assim, f ´ parcial recursiva se e somente se
e
∃s ∈ PR φs(x) (y) = f (x, y). Ent˜o, f ´ comput´vel se
a e a
e somente se cada argumento e a fun¸ao x → f (x, )
c˜
´ comput´vel;
e a
• Isto significa que computacionalmente f est´ em
a
N × N → N se e somente se x → f (x, ) est´ em
a
N → (N → N);
• Similarmente, na categoria cartesiana C vamos supor,
para qualquer f : c × a → b, a existˆncia de um
e
morfismo que faz o mesmo que s em x → f (x, ) na
teoria da recurs˜o. Este morfismo ´ o h.
a e

128. 17 OBJETO EXPONENCIAL 128
C ´ uma categoria cartesiana fechada (CCC) se e somente
e
se:
1. C ´ cartesiana;
e
2. Para cada par a, b ∈ ObC existe um exponencial.
• Exemplo: Set;
• Contra-exemplo: EN. Basta ver que EN[N, N] = R,
onde R s˜o as fun¸˜es (totais) recursivas. Ent˜o, eval
a co a
seria a fun¸ao universal para R, o que ´ um absurdo.
c˜ e

129. 17 OBJETO EXPONENCIAL 129
Teorema 5 Seja C uma CCC, ent˜o ab×c ∼ (ab )c .
a =

130. 17 OBJETO EXPONENCIAL 130
Teorema 6 Seja C uma CCC. Se a a via
(ina : a → a , outa : a → a) e b b via
(inb : b → b , outb : b → b), ent˜o ba b a via
a
(Λ(inb ◦ eval ◦ (id × outa )) : ba →
b a , Λ(outb ◦ eval ◦ (id × ina )) : b a → ba ).
Prova:
Λ(outb ◦ eval ◦ (id × ina )) ◦ Λ(inb ◦ eval ◦ (id × outa )) =
Λ(outb ◦ eval ◦ (id × ina ) ◦ Λ(inb ◦ eval ◦ (id × outa )) × id) =
Λ(outb ◦ eval ◦ Λ(inb ◦ eval ◦ (id × outa )) × id ◦ (id × ina )) =
Λ(outb ◦ (inb ◦ eval ◦ id × outa ) ◦ (id × ina )) =
Λ(eval ◦ id × (outa ◦ ina )) = Λ(eval ◦ id × id) = id

131. 17 OBJETO EXPONENCIAL 131
Seja C uma CCC. Um objeto V de C ´ reflexivo se e
e
somente se V V V .

132. 17 OBJETO EXPONENCIAL 132
Teorema 7 Sejam C uma CCC e V um objeto reflexivo.
Ent˜o t V e V × V V .
a
Prova: Seja (in : V V → V, out : V → V V ) o par de
retra¸˜o entre V e V V . Para provar t V basta provar a
ca
existˆncia de um morfismo de t para V . Seja
e
p1 : t × V → V uma proje¸˜o, ent˜o Λ(p1 ) : t → V V e
ca a
in ◦ Λ(p1 ) : t → V .
Para provar V × V V devemos provar V × V V V e
V × V V segue por composi¸˜o (prova completa
ca
mostrada no livro).

133. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 133
18 Equalizador, Produto Fibrado
e Soma Amalgamada
• Sejam f, g : A → B um par de fun¸oes “paralelas”
c˜
em Set. O subconjunto E ⊆ A no qual f e g
coincidem ´ chamado equalizador de f e g;
e

134. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 134
• Na linguagem de categorias, E deve ser representado
por um sub-objeto, como uma seta mono i : E → A e
i deve satisfazer f ◦ i = g ◦ i;
E A B
f
i
g

135. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 135
• Para garantir que i represente o sub-objeto
“maximal” devemos adicionalmente exigir que se
h : C → A ´ outra fun¸ao tal que f ◦ h = g ◦ h, ent˜o
e c˜ a
h “fatora” de forma unica por meio de i, ou seja,
´
existe apenas um k : C → E tal que h = i ◦ k.

136. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 136
E A B
f
i
g
k
h
C

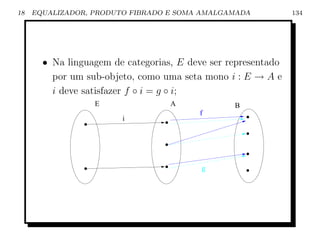
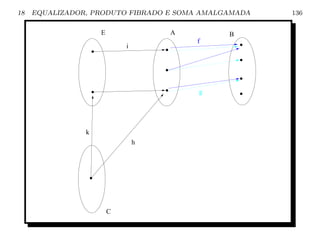
137. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 137
Dado um par de morfismos f, g ∈ C[a, b], um equalizador
de f e g ´ um par (e, i), e ∈ ObC e i ∈ C[e, a] tal que:
e
1. f ◦ i = g ◦ i;
2. Para todo h ∈ C[c, a], f ◦ h = g ◦ h implica que existe
um unico k ∈ C[c, e] tal que i ◦ k = h.
´
f
i Ga G
e
y c Gb
ÐÐÐ g
k ÐÐÐ
ÐÐ h
c
Observa¸˜o: Chamamos h de pr´-equalizador.
ca e

138. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 138
O conceito dual de equalizador ´ o co-equalizador (basta
e
inverter as setas).

139. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 139
Teorema 8 Todo equalizador ´ mono.
e
Prova: Seja i : e → a um equalizador de f, g : a → b.
Assim, f ◦ i = g ◦ i. Sejam j, l : c → e tal que i ◦ j = i ◦ l
(hip´tese). Desde que
o
f ◦ (i ◦ j) = (f ◦ i) ◦ j = (g ◦ i) ◦ j = g ◦ (i ◦ j) ent˜o i ◦ j
a
´ um pr´-equalizador de f e g e existe um unico k : c → e
e e ´
tal que i ◦ j = i ◦ k. Assim, j = k = l.
f
i Ga G
e
y Gb
ÐÐc g
k ÐÐÐ
ÐÐÐ i◦j
c

140. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 140
Teorema 9 Todo equalizador epi ´ iso.
e
Prova: Seja i : e → a um equalizador de f, g : a → b.
Como i ´ epi e f ◦ i = g ◦ i, ent˜o f = g. Logo, a
e a
identidade ida equaliza f e g (´ um pr´-equalizador) e
e e
existe um unico k : a → e tal que ida = i ◦ k. Al´m disto,
´ e
i ◦ k ◦ i = ida ◦ i = i = i ◦ ide e desde que i ´ mono (pelo
e
Teorema 8) ent˜o k ◦ i = ide .
a
e i G a f =g G b
y c
ÐÐÐ
k ÐÐÐ
ÐÐ ida
a

141. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 141
• Queremos generalizar os equalizadores para
morfismos com diferentes origens;
• Este conceito se chama produto fibrado (pullback );
• O produto fibrado ´ uma das no¸˜es mais poderosas
e co
de Teoria das Categorias.

142. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 142
Dadas duas setas f : b → a e g : c → a com destino
comum a, o produto fibrado de (f, g) ´ um objeto b ×a c e
e
duas setas p : b ×a c → b e q : b ×a c → c tal que:
1. f ◦ p = g ◦ q, onde f ◦ p, g ◦ q : b ×a c → a;
2. Para qualquer outra tripla (d, h : d → b, k : d → c) tal
que g ◦ k = f ◦ h, existe uma unica seta
´
h, k a : d → b ×a c tal que p◦ h, k a = h e
q◦ h, k a = k.

143. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 143
d ii
ii k
i
h,ka
ii4
6G
b ×a c q c
h
p g
0 f
b Ga

144. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 144
Observa¸˜es:
co
• O “quadrado” de baixo ´ chamado de “quadrado do
e
produto fibrado” (“pullback square”);
• Note a semelhan¸a entre o produto fibrado e o
c
produto;
• Na verdade, o produto ´ um caso particular de
e
produto fibrado;

145. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 145
• Observe que os subscritos “a” indicam dependˆncia
e
de b ×a c e h, k a sobre f e g, mas os subscritos
n˜o s˜o opcionais pois a nota¸˜o deve indicar quando
a a ca
se trata de um produto fibrado;
• Exemplo de produto fibrado em Set: o produto
fibrado de (f : B → A, g : C → A) ´ e
({(x, y)|x ∈ B, y ∈ C, f (x) = g(y)}, p1 , p2 ), onde
p1 ((x, y)) = x e p2 ((x, y)) = y.

146. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 146
O conceito dual de produto fibrado ´ a soma
e
amalgamada (pushout).

147. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 147
Teorema 10 Seja C uma categoria com objeto terminal
t. Se C tem produtos fibrados para todo par de setas,
ent˜o C tamb´m tem produtos para todo par de objetos.
a e
Prova: (esbo¸o) Dados a, b ∈ C, seja
c
(a × b, p1 : a × b → a, p2 : a × b → b) um produto fibrado
´ a
de (!a : a → t, !b : b → t). E f´cil verificar que este ´ um
e
produto.

148. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 148
Teorema 11 Se uma categoria C tem produtos fibrados
para todo par de setas e tem objeto terminal, ent˜o tem
a
um equalizador para todo par de setas.
Prova: Sejam f, g : a → b. Seja
(c, fst : c → a, snd : c → a) um produto fibrado de
( f, ida : a → b × a, g, ida : a → b × a). Ent˜o o a
equalizador de f, g ´ (c, fst = snd). Pois,
e
f ◦ fst = p1 ◦ f ◦ fst, fst = p1 ◦ f, ida ◦fst = p1 ◦
g, ida ◦snd = p1 ◦ g ◦ snd, snd = g ◦ snd. Al´m disto,
e
para qualquer (c , h : c → a) tal que f ◦ h = g ◦ h, tamb´m e
f, ida ◦h = g, ida ◦h, e por defini¸˜o de produto
ca
fibrado, existe um unico k : c → c tal que fst ◦ k = h.
´

149. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 149
Lema 1 (Lema do Produto Fibrado - Pullback Lemma -
PBL) Se um diagrama da forma:
◦ G◦ G◦
◦ G◦ G◦
comuta, ent˜o:
a
1. Se os dois quadrados menores s˜o produtos fibrados,
a
ent˜o o retˆngulo externo ´ um produto fibrado;
a a e
2. Se o retˆngulo externo e o quadrado a direita s˜o
a a
produtos fibrados, ent˜o o quadrado a esquerda ´ um
a e
produto fibrado.

150. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 150
Teorema 12 Se o quadrado:
b ×a c Gc
q
p g
f
b Ga
´ um produto fibrado e g ´ mono, ent˜o p tamb´m ´
e e a e e
mono.

151. 18 EQUALIZADOR, PRODUTO FIBRADO E SOMA AMALGAMADA 151
Observa¸˜es:
co
• Esta ultima propriedade sugere uma generaliza¸ao de
´ c˜
uma constru¸ao conjunto-teor´tica;
c˜ e
• Se f : A → B ´ uma fun¸ao e C ⊆ B, ent˜o a
e c˜ a
imagem inversa de C sob f , denotada por f −1 (C) ´ o
e
subconjunto de A definido como
´ a
f −1 (C) = {x|x ∈ A, f (x) ∈ C}. E f´cil mostrar que o
diagrama:
f∗
f −1
(C) GC
in in
f
A GB
´ um quadrado de produto fibrado em Set.
e

152. 19 MORFISMOS PARCIAIS 152
19 Morfismos Parciais
• Aplicar Teoria das Categorias no contexto de Teoria
da Computabilidade;
• Neste contexto, a no¸˜o de parcialidade aparece
ca
naturalmente pois programas de computador podem
eventualmente n˜o terminar;
a

153. 19 MORFISMOS PARCIAIS 153
• Uma fun¸ao parcial f : A → B com campo de
c˜
defini¸˜o D ⊆ A pode ser representada por um par
ca
de fun¸oes totais (i : D → A, h : D → B), onde i ´
c˜ e
uma inje¸ao e h ´ a restri¸ao de f para D.
c˜ e c˜

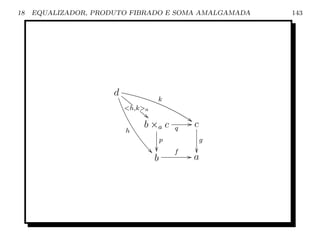
154. 19 MORFISMOS PARCIAIS 154
Dados uma categoria C e dois objetos a e b, um
mapeamento parcial [m, h] : a → b ´ uma classe de
e
equivalˆncia de pares (m : d → a, h : d → b), onde m ´
e e
mono, com respeito a seguinte rela¸ao R:
c˜
(m : d → a, h : d → b)R(m : d → a, h : d → b) se e
somente se existir k : d → d, k iso, m = m ◦ k e
h = h ◦ k.

155. 19 MORFISMOS PARCIAIS 155
• Desejamos definir a categoria pC, de mapeamentos
parciais sobre C;
• Um problema ´ definir as composi¸oes;
e c˜
• Se C tem produtos fibrados para todo par de setas,
podemos resolver o problema;

156. 19 MORFISMOS PARCIAIS 156
• Dados (n : e → b, k : e → c) e (m : d → a, h : d → b);
• Defina [n, k] ◦ [m, h] : a → c a classe de equivalˆncia
e
determinada pelos lados mais externos do seguinte
diagrama, ou seja,
(m ◦ n : d ×b e → a, k ◦ h : d ×b e → c), onde o
quadrado ´ um produto fibrado:
e
h Ge k Gc
d ×b e
n n
d Gb
h
m
a
• Pelo Teorema 12, como n ´ mono, n tamb´m o ´.
e e e

157. 19 MORFISMOS PARCIAIS 157
Exemplo em Set:
• Supomos D ⊆ A e E ⊆ B e tomamos m : D → A e
n : E → B como as inje¸oes canˆnicas;
c˜ o
• Ent˜o, D ×B E = {(x, y)|x ∈ D, y ∈ E, h(x) =
a
n(y)} = {(x, y)|x ∈ D, y ∈ E, h(x) = y} ∼ {x|x ∈
=
D, h(x) ∈ E}, ou seja, o campo de defini¸ao da
c˜
fun¸˜o composta;
ca
• Concluimos que, para todo x ∈ {x|x ∈ D, h(x) ∈ E},
temos k(h (x)) = k(h(x)), como era necess´rio.
a

158. 19 MORFISMOS PARCIAIS 158
Toda seta f ∈ C[a, b] tem naturalmente uma seta
associada em pC, isto ´, (id : a → a, f : a → b).
e

159. 20 ¸˜
FUNTORES E TRANSFORMACOES NATURAIS 159
20 Funtores e Transforma¸oes
c˜
Naturais