Sistemas digitais - Exercícios de portas lógicas

Caderno de exercícios
Sistemas digitais - Portas lógicas

de 102
Índice
Introdução........................................................................................................................................................... 5
Exercícios com portas elementares [AND OR NOT]................................................................................................ 7
Desafio 1 – [AND] com 3 entradas A B C............................................................................................................. 8
Desafio 1.1 – [AND NOT] Tendo em conta a expressão A . 𝐵 ........................................................................... 9
Desafio 1.2 –[ANDNOT] Tendo em conta a expressão A.B.𝐶 ........................................................................ 10
Desafio 2 – [OR] com 3 entradas A B C............................................................................................................. 11
Desafio 2.1 –[OR NOT] Tendoem conta a expressão A + 𝐵........................................................................... 12
Desafio 2.2–[OR NOT] Tendo em conta a expressão A+B+𝐶.......................................................................... 13
Desafio 3 – [OR AND] Tendo em conta a expressão (A+B).C............................................................................... 14
Desafio 3.1 – [OR AND] Tendo em conta a expressão (A.B)+C...................................................................... 15
Desafio 3.2 –[OR ANDNOT] Tendo em conta a expressão (𝐴+B).C ............................................................... 16
Exercícios de consolidação. Portas Elementares [AND OR NOT]........................................................................... 17
DesafioA– DesafioA - Agrupa todasas expressõesnumasótabelae compara os valorespondo-osemevidência
(com cor de fundo amarela) na tabela de verdade............................................................................................ 17
Desafio 4 – [OR AND NOT] Tendoem conta a expressão A + BC + 𝐷 ................................................................ 18
Desafio 4.1 – [OR AND NOT] Tendo em conta a expressão A.𝐵 +𝐶.D ........................................................... 19
Desafio 4.2 – [OR AND NOT] Tendo em conta a expressão A + BC . 𝐷 .......................................................... 20
Desafio 4.3 – [OR AND NOT] Tendo em conta a expressão A + B+C . 𝐷 ........................................................ 21
Desafio 4.4 – [OR AND NOT] Tendo em conta a expressão 𝐴 + B𝐶 . 𝐷.......................................................... 22
Desafio 4.5 – [OR AND NOT] Tendo em conta a expressão 𝐴 + BC . 𝐷.......................................................... 23
Exercícios com portas [NAND NOR].................................................................................................................... 24
Desafio 5 – [AND NOT] Tendo em conta a expressão 𝑨 .𝑩............................................................................. 25
Desafio 5.1 – [NAND] Tendoem conta a expressão 𝐴. 𝐵............................................................................. 25
Desafio 5.2 – [AND OR NAND] Tendo em conta a expressão AB + 𝐴𝐶............................................................. 26
Desafio 5.3 – [AND OR NAND] Tendoem conta a expressão A+B + 𝐴𝐶.......................................................... 27
Desafio 6 – [OR NOT NOR] Tendo em conta a expressão 𝐴 +𝐵 ......................................................................... 28
Desafio 6.1 – [NOR] Tendo em conta a expressão 𝐴 + 𝐵.............................................................................. 28
Desafio 6.2 – [AND OR NOR] Tendo em conta a expressão A+B . 𝐴 + 𝐶......................................................... 29
Desafio 6.3 – [AND OR NOR] Tendoem conta a expressão A.B . 𝐴 + 𝐶......................................................... 30
Exercícios com portas [XOR XNOR] ..................................................................................................................... 31
Desafio 7 – [AND OR NOT] Tendoem conta a expressão 𝑺 = A. 𝐵 + 𝐴.B......................................................... 32
Desafio 7.1 – [XOR] Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵..................................................................... 32
Desafio 8 – [AND OR NOT] Tendoem conta a expressão S = A.B +𝐴.𝐵............................................................ 33
Desafio 8.1 – [XNOR] Tendoem conta a expressão 𝑆 = 𝐴 ⊕ 𝐵................................................................... 33
Desafio De Morgan – Tendo em conta os teoremas de De Morgan .................................................................... 34
Extrair expressões Booleanas de tabelas de verdade........................................................................................... 35
Desafio C – Tendo em conta a tabela de verdade expressão A + B..................................................................... 35

de 102
Desafio 9 – Tendo em conta a tabela de verdade.............................................................................................. 37
Comprovação das propriedades: comutativa, associativa e distributiva.............................................................. 38
Comprovação da regra de precedência das operações lógicas........................................................................... 38
Desafio 9.1 – Tendo em conta a tabela de verdade........................................................................................ 40
Desafio 9.2 – Tendo em conta a tabela de verdade........................................................................................ 41
Extrair expressões Booleanas de circuitos lógicos................................................................................................ 42
Desafio 10 – Tendo em conta o circuitológico.................................................................................................. 42
Desafio 10.1 – Tendo em conta o circuito lógico............................................................................................ 43
Extrair expressões Booleanas de tabelas de verdade. Simplificar pelo método de karnaugh ................................ 46
Desafio 11 – Tendo em conta a tabela de verdade............................................................................................ 47
Desafio 11.1 – Tendo em conta a tabela de verdade...................................................................................... 48
Desafio 12 – Tendo em conta a tabela de verdade............................................................................................ 52
Criar circuitos lógicos com chips de circuitos integrados recorrendo a um simulador online................................. 56
Desafio 13 – Utilizando o Chip 7408.............................................................................................................. 56
Resolução dos exercícios propostos.................................................................................................................... 57
Resolução exercícios com portas elementares [AND OR NOT] ............................................................................. 58
Desafio 1 Resolução – [AND] com 3 entradas A B C........................................................................................... 58
Desafio 1.1 –Resolução [AND NOT] Tendo em conta a expressão A . 𝐵 ......................................................... 59
Desafio 1.2 – Resolução [AND NOT] Tendoem conta a expressão A.B.𝐶........................................................ 60
Desafio 2 – Resolução [OR] com 3 entradas A B C............................................................................................. 61
Desafio 2.1 – Resolução [OR NOT] Tendo em conta a expressão A + 𝐵.......................................................... 62
Desafio 2.2–Resolução[OR NOT] Tendoem conta a expressão A+B+𝐶.......................................................... 63
Desafio 3 –Resolução [ORAND] Tendo em conta a expressão (A+B).C............................................................... 64
Desafio 3.1 – Resolução [OR AND] Tendoem conta a expressão (A.B)+C .................................................... 65
Desafio 3.2 – Resolução [OR AND NOT] Tendo em conta a expressão (𝐴+B).C.............................................. 66
DesafioA– ResoluçãoDesafioA - Agrupatodas as expressõesnumasótabelae comparaos valorespondo-osem
evidência(com cor de fundo amarela) na tabela de verdade............................................................................. 67
Desafio 4 – Resolução [ORAND NOT] Tendoem conta a expressão A + BC + 𝐷 ................................................ 68
Desafio 4.1 – Resolução [OR AND NOT] Tendo em conta a expressão A.𝐵 +𝐶.D........................................... 69
Desafio 4.2 – Resolução [OR AND NOT] Tendo em conta a expressão A + BC . 𝐷 .......................................... 70
Desafio 4.3 – Resolução [OR AND NOT] Tendoem conta a expressão A + B+C . 𝐷 ......................................... 71

de 102
Desafio 4.4 – Resolução [OR AND NOT] Tendoem conta a expressão 𝐴 + B𝐶 . 𝐷 .......................................... 72
Desafio 4.5 – Resolução[OR AND NOT] Tendo em conta a expressão 𝐴 + BC . 𝐷.......................................... 73
Desafio 5 – Resolução [AND NOT] Tendo em conta a expressão 𝑨 .𝑩............................................................. 74
Desafio 5.1 –Resolução [NAND] Tendo em conta a expressão 𝐴. 𝐵.............................................................. 74
Desafio 5.2 – Resolução [AND OR NAND] Tendo em conta a expressão AB + 𝐴𝐶............................................. 75
Desafio 5.3 – Resolução [AND OR NAND] Tendoem conta a expressão A+B + 𝐴𝐶.......................................... 76
Desafio 6 – Resolução [ORNOT NOR] Tendo em conta a expressão 𝐴 +𝐵 ......................................................... 77
Desafio 6.1 – Resolução [NOR] Tendoem conta a expressão 𝐴 + 𝐵.............................................................. 77
Desafio 6.2 – Resolução Tendo em conta a expressão A+B . 𝑨 + 𝑪 ................................................................ 78
Desafio 6.3 – Resolução Tendo em conta a expressão A.B . 𝑨 + 𝑪................................................................. 79
Desafio 7 – Resolução Tendo em conta a expressão 𝑺 = A. 𝐵 + 𝐴.B................................................................. 80
Desafio 7.1 – Resolução Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵................................................................ 80
Desafio 8 – Resolução Tendo em conta a expressão S = A.B +𝐴.𝐵.................................................................... 81
Desafio 8.1 – Resolução Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵................................................................ 81
Desafio De Morgan – Resolução Tendo em conta os teoremas de De Morgan.................................................... 82
Desafio 9 – Resolução Tendo em conta a tabela de verdade.............................................................................. 83
Desafio 9.1 – Resolução Tendo em conta a tabela de verdade........................................................................ 84
Desafio 10 – Resolução Tendoem conta o circuitológico.................................................................................. 87
Desafio 10.1 – Resolução Tendoem conta o circuito lógico............................................................................ 88
Desafio 11 – Resolução Tendoem conta a tabela de verdade............................................................................ 91
Desafio 11.1 – Resolução Tendoem conta a tabela de verdade...................................................................... 92
Desafio 12 – Resolução Tendoem conta a tabela de verdade............................................................................ 96
Desafio 12.2 – Resolução Tendoem conta a tabela de verdade.....................................................................100
Criar circuitos lógicos com chips de circuitos integrados recorrendo a um simulador online................................102
Desafio 13 – Resolução Utilizando o Chip 7408.............................................................................................102

de 102
Introdução
Este manual tem como objetivo abordar o tema relacionado com as portas lógicas de uma forma simplese gradual.
Atravésda resoluçãode exercíciospráticospretende-se que osalunosdesenvolvamosseusconhecimentosde forma
progressiva. Além dos exercícios este manual comtempla também a resolução de todos os exercícios propostos.
O manual é composto por exercícios/Desafios, que se podem subdividir em doistipos distintos. Desafios de prática,
sendoque o seupropósitoé por emprática conhecimentosadquiridos.Desafiosde comprovação,sendoopropósito
destes comprovar teorias ou evidencias relacionadas com este tema.
Sendo que este manual é apenas um caderno de exercícios, todos os temas abordados devem ser previamente
expostos aos alunos para que estes fiquem capacitados dos conhecimentos necessários para a sua elaboração. A
ordemdosexercíciosfoi pensadacomo objetivode acrescentarumgraude dificuldadegradual,contudoestaordem
pode ser alterada em função das necessidades de quem os aplicar.
Recursos:
Software: Logisim (Download https://sourceforge.net/projects/circuit/). É um software simples e intuitivo para a
criação de circuitos lógicos.
O Tinkercad (Inscrição https://www.tinkercad.com/). É uma plataforma on-line que permite criar projetos baseados
em chips de circuitos integrados.
Assuntos abordados:
Portas lógicas
Tabelas de Verdade
Circuitos lógicos
Diagramas temporais
Simplificação de expressões lógicas pelo método de Karnaugh e álgebra booleana
Conteúdos
- Os operadoreslógicosnot,and,or,xor,xnor,nand,nor,buffer,respetivaspropriedadese símbolos lógicos.
- Conceitode variável e funçãobooleana.
- TeoremasdaÁlgebrade Boole.
- A tabelade verdade:formade expressarumproblemaemlógica.Expressõese funçõesbooleanas.
- Desenhode circuitoslógicosapartirde funçõesbooleanas.
- Simplificaçãoalgébricade funçõesbooleanasusandoaspropriedadesdosoperadoreslógicose osteoremasda
álgebrade boole.
- O mapa de Karnaughcomo uma organizaçãode espaçosequivalenteàtabelade verdade.
- Passagemde funçõesbooleanasparao mapade Karnaugh.
- Simplificaçãode funções,apartirdomapa de Karnaugh.Justificaçãodométodo.

de 102
As portas lógicas são o centro da eletrónica digital. Uma porta é um dispositivo eletrónico usado para calcular a função de um sinal
tendo por base dois valores de entrada.
Basicamente, todas as portas lógicas têm uma saída e duas entradas. Algumas portas lógicas como a NOT ou Inverter e o Buffer têm
apenas uma entrada e uma saída. As entradas das portas lógicas são projetadas para receber apenas dados binários (0 ou 1.

de 102
Exercícios com portas elementares [AND OR NOT]
PORTA SÍMBOLO CIRCUITO ELETRICO TABELA DE VERDADE DIAGRAMA TEMPORAL
AND
Entradas
Saída
A . 𝑩
A B S
0 0 0
0 1 0
1 0 0
1 1 1
A 0 0 1 1
B 0 1 0 1
S 0 0 0 1
OR
Entradas
Saída
A+ 𝑩
A B S
0 0 0
0 1 1
1 0 1
1 1 1
A 0 0 1 1
B 0 1 0 1
S 0 1 1 1
NOT
Entradas
Saída
𝐴
A S
0 1
1 0

de 102
Porta Lógica - Logic Gate AND ou E ou *
Desafio 1 – [AND] com 3 entradas A B C
a) Calcularo nº de saídas possíveis.
b) Desenharo circuitonologisim.
c) Desenharodiagrama temporal.
d) Desenharo circuitoelétricoequivalente.
e) Preencheratabelade verdade.
f) Conclusão.
Resolução
a) Calcularo nº de saídas possíveis.Resposta23
=8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
e) Preencheratabelade verdade
Entradas
Saída
S=A.B.C
A B C
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
f) Conclusão.

de 102
Porta NOT ou INVERTER (inversor)
Desafio 1.1 – [AND NOT] Tendo em conta a expressão A . 𝐵
b) Preencheratabelade verdade.
c) Desenharocircuitono logisim.
d) Desenharo diagramatemporal.
e) Conclusão.
Resolução
=_______
b) Preencheratabelade verdade
Entradas
Saída
A . 𝑩
A B 𝑩 S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Desafio 1.2 –[AND NOT] Tendo em conta a expressão A.B.𝐶̅
e) Conclusão.
Resolução
=_____
23
=8
Entradas
Saída
A.B.𝑪̅
A B C 𝑪̅ S
1
2
3
4
5
6
7
8
c) Desenharocircuitono logisim.(No logisimresolve o exercícioutilizandoportas de 3 entradas e utilizandoportas de apenas 2
entradas)
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
e) Conclusão.

de 102
Porta Lógica - Logic Gate OR ou OU ou +
Desafio 2 – [OR] com 3 entradas A B C
a) Calcularo nº de saídas possíveis
b) Desenharo circuitonologisim
c) Desenharodiagrama temporal
d) Desenharo circuitoelétricoequivalente
f) Conclusão
Resolução
=8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
Entradas
Saída
S=A+B+C
f) Conclusão.

de 102
Desafio 2.1 –[OR NOT] Tendo em conta a expressão A + 𝐵
e) Conclusão.
Resolução
=_____
Entradas
Saída
A + 𝑩
A B 𝑩 S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Porta Lógica- Logic Gate OR ou OU ou +
Desafio 2.2–[OR NOT] Tendo em conta a expressão A+B+𝐶̅
e) Conclusão.
Resolução
=_____
23
=8
Entradas
Saída
A+B+𝑪̅
A B C 𝑪̅ S
1
2
3
4
5
6
7
8
entradas)
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
e) Conclusão.

de 102
Desafio 3 – [OR AND] Tendo em conta a expressão (A+B).C
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
(A+B).C
A B C (A+B) S
1
2
3
4
5
6
7
8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 3.1 – [OR AND] Tendo em conta a expressão (A.B)+C
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
(A.B)+C
A B C (A.B) S
1
2
3
4
5
6
7
8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 3.2 –[OR AND NOT] Tendo em conta a expressão (𝐴̅+B).C
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
(𝑨̅+B).C
A B C 𝑨̅ (𝑨̅+B) S
1
2
3
4
5
6
7
8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Exercícios de consolidação. Portas Elementares [AND OR NOT]
DesafioA – Desafio A - Agrupa todas as expressões numa só tabela e compara os valores pondo-os
em evidência (com cor de fundo amarela) na tabela de verdade.
Resolução
=____
23
=8
Entradas
Saída
(A+B).C
Saída
(A.B)+C
Saída
(𝑨̅+B).C
A B C 𝑨̅ (A+B) (A.B) (𝑨̅+B) S S S
1
2
3
4
5
6
7
8
b) Conclusão.

de 102
Desafio 4 – [OR AND NOT] Tendo em conta a expressão A + BC + 𝐷̅
e) Conclusão.
Resolução
=____
Entradas
A B C D D’ BC A + BC + 𝑫̅
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 4.1 – [OR AND NOT] Tendo em conta a expressão A.𝐵̅ +𝐶̅.D
e) Conclusão.
Resolução
=____
Entradas
A B C D 𝑩̅ 𝑪̅ A.𝑩̅ 𝑪̅.D A.𝑩̅ +𝑪̅.D
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 4.2 – [OR AND NOT] Tendo em conta a expressão A + BC . 𝐷̅
e) Conclusão.
Resolução
=____
Entradas
A B C D D’ BC A + BC . 𝑫̅
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 4.3 – [OR AND NOT] Tendo em conta a expressão A + B+C . 𝐷̅
e) Conclusão.
Resolução
=____
Entradas
A B C D D’ A + B+C . 𝑫̅
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 4.4 – [OR AND NOT] Tendo em conta a expressão 𝐴 + B𝐶 . 𝐷̅
e) Conclusão.
Resolução
=____
Entradas
A B C D D’ BC 𝑨 𝑨 + B𝑪 . 𝑫̅
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 4.5 – [OR AND NOT] Tendo em conta a expressão 𝐴 + BC . 𝐷̅
e) Conclusão.
Resolução
=____
Entradas
A B C D 𝑨 + BC . 𝑫̅
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Exercícios com portas [NAND NOR]
PORTA SÍMBOLO TABELA DE VERDADE DIAGRAMA TEMPORAL
NAND
Entradas
Saída
𝑨 . 𝑩
A B S
0 0 1
0 1 1
1 0 1
1 1 0
A 0 0 1 1
B 0 1 0 1
S 1 1 1 0
NOR
Entradas
Saída
𝐀 + 𝐁
A B S
0 0 1
0 1 0
1 0 0
1 1 0
A 0 0 1 1
B 0 1 0 1
S 1 0 0 0

de 102
Porta Lógica - Logic Gate NAND (Não E)
Desafio 5 – [AND NOT] Tendo em conta a expressão 𝑨̅ .𝑩̅
Desafio 5.1 – [NAND] Tendo em conta a expressão 𝐴. 𝐵̅̅̅̅̅
e) Conclusão.
Resolução
=____
b) Preencherastabelasde verdade
22
=4
Entradas
Saída
𝑨̅ .𝑩̅
A B 𝑨̅ 𝑩̅ S
1
2
3
4
22
=4
Entradas
Saída
𝑨. 𝑩̅̅̅̅̅
A B A.B S
1
2
3
4
b) Desenharos circuitosnologisim.
c) Desenharosdiagramastemporais.
A 0 0 1 1
B 0 1 0 1
S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Desafio 5.2 – [AND OR NAND] Tendo em conta a expressão AB + 𝐴𝐶
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
AB + 𝑨𝑪
A B C AB AC 𝑨𝑪 S
0
1
2
3
4
5
6
7
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 5.3 – [AND OR NAND] Tendo em conta a expressão A+B + 𝐴𝐶
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
A+B + 𝑨𝑪
0
1
2
3
4
5
6
7
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Portas Lógica - Logic Gate NOR (Não OU)
Desafio 6 – [OR NOT NOR] Tendo em conta a expressão 𝐴̅ +𝐵̅
Desafio 6.1 – [NOR] Tendo em conta a expressão 𝐴 + 𝐵̅̅̅̅̅̅̅̅
e) Conclusão.
Resolução
=____
22
=4
Entradas
Saída
𝑨̅ +𝑩̅
A B 𝑨̅ 𝑩̅ S
1
2
3
4
22
=4
Entradas
Saída
𝑨 + 𝑩̅̅̅̅̅̅̅̅
A B A+B S
1
2
3
4
A 0 0 1 1
B 0 1 0 1
S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Desafio 6.2 – [AND OR NOR] Tendo em conta a expressão A+B . 𝐴 + 𝐶
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
A+B . 𝑨 + 𝑪
A B C S
0
1
2
3
4
5
6
7
b) Desenharo circuitono logisim.
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Desafio 6.3 – [AND OR NOR] Tendo em conta a expressão A.B . 𝐴 + 𝐶
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
A.B . 𝑨 + 𝑪
A B C S
0
1
2
3
4
5
6
7
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S
f) Conclusão.

de 102
Exercícios com portas [XOR XNOR]
PORTA SÍMBOLO TABELA DE VERDADE DIAGRAMA TEMPORAL
XOR
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
0 0 0
0 1 1
1 0 1
1 1 0
A 0 0 1 1
B 0 1 0 1
S 0 1 1 0
XNOR
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
0 0 1
0 1 0
1 0 0
1 1 1
A 0 0 1 1
B 0 1 0 1
S 1 0 0 1

de 102
Comprove que a expressão 𝐀. 𝑩 + 𝑨. 𝐁 Equivale à porta XOR
Porta Lógica- Logic GateXOR⊕
Porta NOTou INVERTER (inversor)
Porta Lógica- Logic GateOR ou OU ou +
Desafio 7 – [AND OR NOT] Tendo em conta a expressão 𝑺 = A. 𝐵 + 𝐴. B
Desafio 7.1 – [XOR] Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵
e) Conclusão.
Resolução
=____
22
=4
Entradas
Saída
A. 𝐵 + 𝐴.B
A B 𝐴 𝐵 A. 𝐵 𝐴. B S
1 0 0
2 0 1
3 1 0
4 1 1
22
=4
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
1 0 0
2 0 1
3 1 0
4 1 1
b) Desenharos circuitosnologisim(Teste oscircuitoscomentradasiguais).
A 0 0 1 1
B 0 1 0 1
S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Comprovequea expressão A.B +𝑨.𝑩 Equivaleà porta XNOR
Porta Lógica- Logic GateXNOR ⊕
Desafio 8 – [AND OR NOT] Tendo em conta a expressão S = A.B + 𝐴. 𝐵
Desafio 8.1 – [XNOR] Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵
e) Conclusão.
Resolução
=____
22
=4
Entradas
Saída
A.B + 𝐴. 𝐵
A B 𝐴 𝐵 A. B 𝐴.𝐵 S
1
2
3
4
22
=4
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
1
2
3
4
A 0 0 1 1
B 0 1 0 1
S
A 0 0 1 1
B 0 1 0 1
S
f) Conclusão.

de 102
Comprovação dos Teoremas de De Morgan
Desafio De Morgan – Tendo em conta os teoremas de De Morgan
a) Comprovaçãoatravésda tabelade verdade.
b) Comprovaçãoatravésdo circuitológico
Resolução
Ordem A B 𝐴 𝐵 𝐴. 𝐵 𝐴 + 𝐵 𝐴. 𝐵 𝐴 + 𝐵 𝐴 + 𝐵 𝐴. 𝐵
0 0 0
1 0 1
2 1 0
3 1 1
Teoremas
de “De
Morgan”
18 𝐴. 𝐵 = 𝐴 + 𝐵
19 𝐴 + 𝐵 = 𝐴. 𝐵
𝐴. 𝐵 = 𝐴 + 𝐵 𝐴 + 𝐵 = 𝐴. 𝐵

de 102
Extrair expressões Booleanas de tabelas de verdade.
Extrair expressões Booleanas de circuitos lógicos.
Simplificar expressões pelo método de karnaugh.
Simplificar expressões pelo método álgebra booleana.
Situação problema – A empresaXPT necessitaque dois funcionários(que se encontram emlocais distintos)
acionemum motor elétricosemque seja necessáriocomunicaremum com o outro.
Desafio C – Tendo em conta a tabela de verdade expressão A + B
b) Retirar a expressãobooleanadatabela
d) Simplificarpelométodode karnaugh
d1) comprovaro resultadonatabelade verdade
d2) Desenharocircuitono logisim.
e) Simplificarpelométododa álgebrabooleana
f) Conclusão.
Resolução
=4
Entradas Saída Expressão b) Expressão booleana
d1) comprovar o resultado
na tabela de verdade
Ordem A B S Soma de produtos A+B
0 0 0 0
𝐴𝐵 + 𝐴𝐵 + 𝐴𝐵
0
1 0 1 1 𝐴𝐵 1
2 1 0 1 𝐴𝐵 1
3 1 1 1 𝐴𝐵 1
c) Desenharo circuito no logisim.

de 102
B 𝐵 B
A+B
A 0 1
𝐴 0
0 0
1
1
A 1 1
2
1
3
𝐴𝐵 + 𝐴𝐵 + 𝐴𝐵 Expressãobooleanaretiradadatabelade verdade
𝐴𝐵 + 𝐴(𝐵 + 𝐵) 14) Propriedade distributivaA.(B + C)= A . B + A . C
𝐴𝐵 + 𝐴(1) 5) Teorema 5 A+A̅=1
𝐴𝐵 + 𝐴 16) Identidadesauxiliares
A+B Resultado
f) Conclusão. A utilização da simplificação algébrica da expressão reduziu o número de
portas utilizadas de 6 para 1.

de 102
Desafio 9 – Tendo em conta a tabela de verdade
Resolução
=____
Ordem A B C S
Expressão
booleana
Expressão booleana método da
soma de produtos (SdP)
0 0 0 0 0
1 0 0 1 1
2 0 1 0 0
3 0 1 1 1
4 1 0 0 1
5 1 0 1 1
6 1 1 0 0
7 1 1 1 0
c) Desenharocircuitono logisim.(Utilizaportasde 3 entradas)

de 102
Comprovação das propriedades: comutativa, associativa e distributiva.
Comprovação da regra de precedência das operações lógicas
Nota o símbolo ≡ significa equivalente
Comprovação da propriedade comutativa
a) Preenche astabelasde verdade
Propriedade comutativa na
adição:
22
=4
Entradas
A B A+B B+A
0 0 0
1 0 1
2 1 0
3 1 1
Propriedade comutativa na
Multiplicação:
22
=4
Entradas
A B A.B B.A
0 0 0
1 0 1
2 1 0
3 1 1
b) Desenhae testaos circuitosno logisim.
Propriedade comutativa na adição: Propriedade comutativa na Multiplicação:
A+B ≡ B+A A.B ≡ B.A
≡ ≡
Comprovação da propriedade associativa
Propriedade associativa na adição:
23
=8
Entradas
A B A + (B + C) (A + B) + C A + B + C
0 0 0
1 0 1
2 1 0
3 1 1
4 0 0
5 0 1
6 1 0
7 1 1
Propriedade associativa na Multiplicação:
23
=8
Entradas
A B A . (B . C) (A . B) . C A . B . C
0 0 0
1 0 1
2 1 0
3 1 1
4 0 0
5 0 1
6 1 0
7 1 1
A + (B + C) ≡ (A + B) + C ≡ A + B + C
≡ ≡
Propriedade associativa na Multiplicação:

de 102
A . (B . C) ≡ (A . B) . C ≡ A . B . C
≡ ≡
Comprovação da propriedade distributiva A.(B+ C)= A . B + A . C
Propriedade distributiva
23
=8
Entradas
A B A. (B + C) A . B + A . C
0 0 0
1 0 1
2 1 0
3 1 1
4 0 0
5 0 1
6 1 0
7 1 1
Propriedade distributiva
A. (B + C) ≡ A . B + A . C
≡
Comprovação da regra de precedência das operações lógicas
Quandonuma mesmaexpressãoBooleanaaparecemoperaçõesEe OU, é necessárioseguiraordemde precedência.
A multiplicação (lógica) tem precedência sobre a adição (lógica). Além disso, expressões entre parêntesis têm
precedência sobre operadores E e OU.
a) Preenche atabelade verdade
Precedênciadas operações Resposta A Resposta B
23
=8
Entradas
A B A + B.C
0 0 0
1 0 1
2 1 0
3 1 1
4 0 0
5 0 1
6 1 0
7 1 1
b) Testa os circuitos no logisim
b1) Qual dos circuitos esta correto?

de 102
Desafio 9.1 – Tendo em conta a tabela de verdade
Resolução
=______
Ordem A B C S
Expressão
booleana
0 0 0 0 1
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4 1 0 0 0
5 1 0 1 0
6 1 1 0 1
7 1 1 1 0

de 102
Resolução
=______
Ordem A B C S
Expressão
booleana
0 0 0 0 0
1 0 0 1 0
2 0 1 0 1
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1
6 1 1 0 0
7 1 1 1 1

de 102
Desafio 10 – Tendo em conta o circuito lógico
b) Retirar a expressãobooleanadocircuito
c) Resolverasaída na tabelade verdade
Resolução
=____
Saída
A B C Expressão booleana
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A
B
C
S
Fase 1 Fase 2 Fase 3

de 102
Desafio 10.1 – Tendo em conta o circuito lógico
Resolução
=____
b) Retirar a expressãobooleanadocircuito.
Saída
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
A
B
C
S
S = …………………………………………………………….

de 102
Resolução
=____
Saída
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
C
B
S
A

de 102
Resolução
=____
Ordem A B C D S
Expressão
booleana
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
12 1 1 0 0
13 1 1 0 1
14 1 1 1 0
15 1 1 1 1

de 102
Extrair expressões Booleanas de tabelas de verdade. Simplificar pelo método de
karnaugh e álgebra de Boole.
Teoremas de Álgebra de
Boole
Ordem Teoremas Ordem Teoremas
1 𝑨 = 𝑨
Propriedade
comutativa
10
Propriedade comutativa na adição:
A+B=B+A
2 A+0=A 11
Propriedade comutativa na multiplicação:
A.B=B.A
3 A+1=1
Propriedade
associativa
12
A + (B + C)=(A + B) + C=A + B + C
4 A+A=A 13
Propriedade associativa na multiplicação:
A . (B . C)=(A . B) . C= A . B . C
5 A+A̅=1
Propriedade
distributiva
14 A. (B + C)= A . B + A . C
6 A*1=A
Identidades
auxiliares
15 A+A.B=A
7 A*0=0 16 A+A’.B=A+B
8 A*A=A 17 (A+B).(A+C)=A+B.C
9 A*A̅=0
Teoremas de
“De Morgan”
18 𝐴. 𝐵 = 𝐴 + 𝐵
19 𝐴 + 𝐵 = 𝐴. 𝐵

de 102
Comprovação da porta XOR
Extrair expressões Booleanas de tabelas de verdade. Simplificar pelo método de karnaugh
f) Conclusão.
Resolução
=____
Ordem A B S Soma de produtos
0 0 0 0
1 0 1 1
2 1 0 1
3 1 1 0
B 𝐵 B
A 0 1
𝐴 0
A 1
e) Simplificarpelométododa álgebrabooleana(Se possível)
f) Conclusão (Procure a conclusãonatabelaque contemtodasas portas lógicas).

de 102
f) Conclusão.
Resolução
=____
11.1
0 0 0 1
1 0 1 1
2 1 0 1
3 1 1 0
B 𝐵 B
A 0 1
𝐴 0
A 1
e) Simplificarpelométododa álgebrabooleana(Consulte a tabelacom os teoremasda álgebrade Boole)
𝐴𝐵 + 𝐴𝐵 + 𝐴 . 𝐵 Expressãobooleanaretiradadatabelade verdade
14) Propriedade distributivaA.(B + C)= A . B + A . C
5) Teorema 5 A+A̅=1
16) Identidadesauxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
Resultado
f) Conclusão.

de 102
f) Conclusão.
Resolução
=____
0 0 0 0
1 0 1 1
2 1 0 1
3 1 1 1
B 𝐵 B
A 0 1
𝐴 0
A 1
16) Identidadesauxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
Resultado
f) Conclusão.

de 102
Comprovação da porta XNOR
f) Conclusão.
Resolução
=____
x
0 0 0 1
1 0 1 0
2 1 0 0
3 1 1 1
B 𝐵 B
A 0 1
𝐴 0
A 1

de 102
f) Conclusão.
Resolução
=____
X2
0 0 0 0
1 0 1 0
2 1 0 1
3 1 1 1
B 𝐵 B
A 0 1
𝐴 0
A 1
𝐴𝐵 + 𝐴𝐵 Expressãobooleanaretiradadatabelade verdade
Resultado
f) Conclusão.

de 102
f) Conclusão.
Resolução
=____
d1) comprovar o
resultado na tabela
de verdade
Ordem A B C S Soma de produtos
0 0 0 0 1
A’B’C’+A’B’C+A’BC’+A’BC+AB’C’+AB’C
1 0 0 1 1
2 0 1 0 1
3 0 1 1 1
4 1 0 0 1
5 1 0 1 1
6 1 1 0 0
7 1 1 1 0
B’+A’

de 102
A’B’C’+A’B’C+A’BC’+A’BC+AB’C’+AB’C Expressãobooleanaretiradadatabelade verdade
A’B’(C’+C)+A’B(C’+C)+AB’(C’+C) 14) Propriedade distributivaA.(B + C)= A . B + A . C
A’B’(1)+A’B(1)+AB’(1) 5) Teorema 5 A+A̅=1
A’B’+A’B+AB’
A’(B’+B)+AB’ 14) Propriedade distributivaA.(B + C)= A . B + A . C
A’(1) +AB’ 5) Teorema 5 A+A̅=1
A’+AB’ 16) IdentidadesAuxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
A’+B’ Resultado
f) Conclusão.

de 102
e) Conclusão.
Resolução
=____
0 0 0 0 1
1 0 0 1 0
2 0 1 0 1
3 0 1 1 0
4 1 0 0 1
5 1 0 1 1
6 1 1 0 1
7 1 1 1 1
d) Simplificarpelométodode karnaugh(Atenção às bordas)
. BC 𝐵 𝐶 𝐵𝐶 𝐵𝐶 𝐵𝐶
A 00 01 11 10
𝐴 0
A 1
e) Conclusão.

de 102
Extrair expressões Booleanas de tabelas de verdade. (AC’+B’C)
e) Simplificarpelométododaálgebrabooleana
f) Conclusão.
Resolução
=____
0 0 0 0 0
1 0 0 1 1
2 0 1 0 0
3 0 1 1 0
4 1 0 0 1
5 1 0 1 1
6 1 1 0 1
7 1 1 1 0
A 00 01 11 10
𝐴 0
A 1
Expressãobooleanaretiradada tabelade verdade
f) Conclusão.

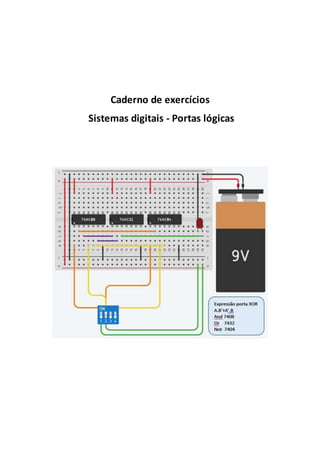
de 102
Criar circuitos lógicos com chips de circuitos integrados recorrendo a um
simulador online.
Circuitos lógicos com Chips de circuitos integrados
Desafio 13 – Utilizando o Chip 7408
a) Analisaa datasheetdochip7408 (corresponde àportaAND). http://www.electroschematics.com/8891/7408-
datasheet/
b) Constrói a expressãoA.Brecorrendoaosimuladoronline disponibilizadoem https://www.tinkercad.com
No final devesobterumcircuitosemelhante àfiguraabaixo.

de 102
Resolução dos exercícios propostos

de 102
Resolução exercícios com portas elementares [AND OR NOT]
Desafio 1 Resolução – [AND] com 3 entradas A B C
e) Preencheratabelade verdade.
f) Conclusão.
Resolução
=8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 0 0 0 0 0 0 1
Entradas
Saída
S=A.B.C
A B C S
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
f) Conclusão.A saída (s) só será 1 quandotodas as entradasforem1.

de 102
Desafio 1.1 –Resolução [AND NOT] Tendo em conta a expressão A . 𝐵
e) Conclusão.
Resolução
=4
Entradas
Saída
A . 𝑩
A B 𝑩 S
0 0 1 0
0 1 0 0
1 0 1 1
1 1 0 0
A 0 0 1 1
B 0 1 0 1
S 0 0 1 0
f) Conclusão. A saída (s) só será 1 quando A=1 e B=0.

de 102
Desafio 1.2 – Resolução [AND NOT] Tendo em conta a expressão A.B.𝐶̅
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
A.B.𝑪̅
A B C 𝑪̅ S
1 0 0 0 1 0
2 0 0 1 0 0
3 0 1 0 1 0
4 0 1 1 0 0
5 1 0 0 1 0
6 1 0 1 0 0
7 1 1 0 1 1
8 1 1 1 0 0
entradas)
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 0 0 0 0 0 1 0
e) Conclusão.
Se A for 1, B for1 e C for0 a saída será1, para as outrasprobabilidadesasaída será0.

de 102
Desafio 2 – Resolução [OR] com 3 entradas A B C
a) Calcularo nº de saídas possíveis
b) Desenharo circuitonologisim
c) Desenharodiagrama temporal
d) Desenharo circuitoelétricoequivalente
f) Conclusão
Resolução
=8
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 1 1 1 1 1 1 1
Entradas
Saída
S=A+B+C
A B C S
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
f) Conclusão.A saída (s) será 1 sempre que umadasentradasseja1.

de 102
Desafio 2.1 – Resolução [OR NOT] Tendo em conta a expressão A + 𝐵
e) Conclusão.
Resolução
=4
Entradas
Saída
A + 𝑩
A B 𝑩 S
0 0 1 1
0 1 0 0
1 0 1 1
1 1 0 1
A 0 0 1 1
B 0 1 0 1
S 1 0 1 1
f) Conclusão. A saída (s) só será 0 quando A=0 e B=1.

de 102
Porta Lógica- Logic Gate OR ou OU ou +
Desafio 2.2–Resolução [OR NOT] Tendo em conta a expressão A+B+𝐶̅
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
A+B+𝑪̅
A B C 𝑪̅ S
1 0 0 0 1 1
2 0 0 1 0 0
3 0 1 0 1 1
4 0 1 1 0 1
5 1 0 0 1 1
6 1 0 1 0 1
7 1 1 0 1 1
8 1 1 1 0 1
entradas)
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 1 0 1 1 1 1 1 1
e) Conclusão.
Se A for 0, B for 0 e C for 1 a saída será 0, para as outras probabilidades a saída será 1.

de 102
Desafio 3 –Resolução [OR AND] Tendo em conta a expressão (A+B).C
e) Conclusão.
Resolução
=_8__
23
=8
Entradas
Saída
(A+B).C
A B C (A+B) S
1 0 0 0 0 0
2 0 0 1 0 0
3 0 1 0 1 0
4 0 1 1 1 1
5 1 0 0 1 0
6 1 0 1 1 1
7 1 1 0 1 0
8 1 1 1 1 1
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 0 0 1 0 1 0 1
f) Conclusão.
Para a saída ser1, o C e o A ou o B (ou osdois) terãode ser 1. Para as outra probabilidadesasaída será0.

de 102
Desafio 3.1 – Resolução [OR AND] Tendo em conta a expressão (A.B)+C
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
(A.B)+C
A B C (A.B) S
1 0 0 0 0 0
2 0 0 1 0 1
3 0 1 0 0 0
4 0 1 1 0 1
5 1 0 0 0 0
6 1 0 1 0 1
7 1 1 0 1 1
8 1 1 1 1 1
b) Desenharo circuitono logisim.
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 1 0 1 0 1 1 1
f) Conclusão.
Para a saída ser1, pelomenosC ouA e B terão de ser1.

de 102
Desafio 3.2 – Resolução [OR AND NOT] Tendo em conta a expressão (𝐴̅+B).C
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
(𝑨̅+B).C
A B C 𝑨̅ (𝑨̅+B) S
1 0 0 0 1 1 0
2 0 0 1 1 1 1
3 0 1 0 1 1 0
4 0 1 1 1 1 1
5 1 0 0 0 0 0
6 1 0 1 0 0 0
7 1 1 0 0 1 0
8 1 1 1 0 1 1
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 1 0 1 0 0 0 1
f) Conclusão.
Para a saída ser1, C e B têmde ser 1.

de 102
DesafioA – ResoluçãoDesafio A - Agrupa todas as expressões numa só tabela e compara os valores
pondo-os em evidência (com cor de fundo amarela) na tabela de verdade.
Resolução
=___8_
23
=8
Entradas
Saída
(A+B).C
Saída
(A.B)+C
Saída
(𝑨̅+B).C
A B C 𝑨̅ (A+B) (A.B) (𝑨̅+B) S S S
1 0 0 0 1 0 0 1 0 0 0
2 0 0 1 1 0 0 1 0 1 1
3 0 1 0 1 1 0 1 0 0 0
4 0 1 1 1 1 0 1 1 1 1
5 1 0 0 0 1 0 0 0 0 0
6 1 0 1 0 1 0 0 1 1 0
7 1 1 0 0 1 1 1 0 1 0
8 1 1 1 0 1 1 1 1 1 1
b) Conclusão.
As saídas4 e 8 sãoiguaisemtodas as expressões

de 102
Desafio 4 – Resolução [OR AND NOT] Tendo em conta a expressão A + BC + 𝐷̅
e) Conclusão.
Resolução
=_16_
Entradas
A B C D D’ BC A + BC + 𝑫̅
0 0 0 0 1 0 1
0 0 0 1 0 0 0
0 0 1 0 1 0 1
0 0 1 1 0 0 0
0 1 0 0 1 0 1
0 1 0 1 0 0 0
0 1 1 0 1 1 1
0 1 1 1 0 1 1
1 0 0 0 1 0 1
1 0 0 1 0 0 1
1 0 1 0 1 0 1
1 0 1 1 0 0 1
1 1 0 0 1 0 1
1 1 0 1 0 0 1
1 1 1 0 1 1 1
1 1 1 1 0 1 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 1
f) Conclusão. A saída só será 0, quandoA=0, B=0, C=0, D=1 ouA=0, B=0, C=1, D=1 ou A=0, B=1, C=0, D=1.

de 102
Desafio 4.1 – Resolução [OR AND NOT] Tendo em conta a expressão A.𝐵̅ +𝐶̅.D
e) Conclusão.
Resolução
=__16__
Entradas
A B C D 𝑩̅ 𝑪̅ A.𝑩̅ 𝑪̅.D A.𝑩̅ +𝑪̅.D
0 0 0 0 1 1 0 0 0
0 0 0 1 1 1 0 1 1
0 0 1 0 1 0 0 0 0
0 0 1 1 1 0 0 0 0
0 1 0 0 0 1 0 0 0
0 1 0 1 0 1 0 1 1
0 1 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0
1 0 0 0 1 1 1 0 1
1 0 0 1 1 1 1 1 1
1 0 1 0 1 0 1 0 1
1 0 1 1 1 0 1 0 1
1 1 0 0 0 1 0 0 0
01 1 0 1 0 1 0 1 1
1 1 1 0 0 0 0 0 0
1 1 1 1 0 0 0 0 0
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 0 1 0 0 0 1 0 0 1 1 1 1 0 1 0 0
f) Conclusão. S=0, quando, todas as entradas forem 0 ou 1 ou A=1, B=1, C=1, D=0 ou A=1, B=1,
C=0, D=0 ouA=0, B=1, C=1, D=1 ou A=0, B=1, C=1, D=0 ou A=0, B=1, C=0, D=0 ouA=0, B=0, C=1, D=1 ou A=0, B=0,
C=1, D=0.

de 102
Desafio 4.2 – Resolução [OR AND NOT] Tendo em conta a expressão A + BC . 𝐷̅
e) Conclusão.
Resolução
=__16__
Entradas
A B C D D’ BC . 𝑫̅ A + BC . 𝑫̅
0 0 0 0 1 0 0
0 0 0 1 0 0 0
0 0 1 0 1 0 0
0 0 1 1 0 0 0
0 1 0 0 1 0 0
0 1 0 1 0 0 0
0 1 1 0 1 1 1
0 1 1 1 0 0 0
1 0 0 0 1 0 1
1 0 0 1 0 0 1
1 0 1 0 1 0 1
1 0 1 1 0 0 1
1 1 0 0 1 0 1
1 1 0 1 0 0 1
1 1 1 0 1 1 1
1 1 1 1 0 0 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1
f) Conclusão. A saída só será0, quandoA=0, B=0, C=0, D=0 ou A=0, B=0, C=0, D=1 ou A=0, B=0, C=1, D=0 ou
A=0, B=0, C=1, D=1 ouA=0, B=1, C=0, D=0 ou A=0, B=1, C=0, D=1 ou A=0, B=1, C=1, D=1.

de 102
Desafio 4.3 – Resolução [OR AND NOT] Tendo em conta a expressão A + B+C . 𝐷̅
e) Conclusão.
Resolução
=__16__
Entradas
A B C D D’ C . 𝑫̅ A + B+C . 𝑫̅
0 0 0 0 1 0 0
0 0 0 1 0 0 0
0 0 1 0 1 1 1
0 0 1 1 0 0 0
0 1 0 0 1 0 1
0 1 0 1 0 0 1
0 1 1 0 1 1 1
0 1 1 1 0 0 1
1 0 0 0 1 0 1
1 0 0 1 0 0 1
1 0 1 0 1 1 1
1 0 1 1 0 0 1
1 1 0 0 1 0 1
1 1 0 1 0 0 1
1 1 1 0 1 1 1
1 1 1 1 0 0 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1
f) Conclusão. A saída só será 0, quando A=0, B=0, C=0, D=0 ou A=0, B=0, C=0, D=1 ou
A=0, B=0, C=1, D=1.

de 102
Desafio 4.4 – Resolução [OR AND NOT] Tendo em conta a expressão 𝐴 + B𝐶 . 𝐷̅
e) Conclusão.
Resolução
=__16__
Entradas
A B C D 𝑨 D’ 𝑪 𝑪 . 𝑫̅ 𝑨 + B+𝑪 . 𝑫̅
0 0 0 0 1 1 1 1 1
0 0 0 1 1 0 1 0 1
0 0 1 0 1 1 0 0 1
0 0 1 1 1 0 0 0 1
0 1 0 0 1 1 1 1 1
0 1 0 1 1 0 1 0 1
0 1 1 0 1 1 0 0 1
0 1 1 1 1 0 0 0 1
1 0 0 0 0 1 1 1 1
1 0 0 1 0 0 1 0 0
1 0 1 0 0 1 0 0 0
1 0 1 1 0 0 0 0 0
1 1 0 0 0 1 1 1 1
1 1 0 1 0 0 1 0 1
1 1 1 0 0 1 0 0 1
1 1 1 1 0 0 0 0 1
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1
f) Conclusão. A saída será 0, quando B=0 ou B e C =0 ou B e D =0

de 102
Desafio 4.5 – Resolução [OR AND NOT] Tendo em conta a expressão 𝐴 + BC . 𝐷̅
e) Conclusão.
Resolução
=_16___
Entradas
A B C D A’ BC D’ 𝑨 + BC . 𝑫̅
0 0 0 0 1 0 1 1
0 0 0 1 1 0 0 1
0 0 1 0 1 0 1 1
0 0 1 1 1 0 0 1
0 1 0 0 1 0 1 1
0 1 0 1 1 0 0 1
0 1 1 0 1 1 1 1
0 1 1 1 1 1 0 1
1 0 0 0 0 0 1 0
1 0 0 1 0 0 0 0
1 0 1 0 0 0 1 0
1 0 1 1 0 0 0 0
1 1 0 0 0 0 1 0
1 1 0 1 0 0 0 0
1 1 1 0 0 1 1 1
1 1 1 1 0 1 0 0
A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
S 1 1 1 1 1 1 1 1 0 0
0
0 0 0 1 0
f) Conclusão.

de 102
Desafio 5 – Resolução [AND NOT] Tendo em conta a expressão 𝑨̅ .𝑩̅
Desafio 5.1 –Resolução [NAND] Tendo em conta a expressão 𝐴. 𝐵̅̅̅̅̅
e) Conclusão.
Resolução
=_4__
22
=4
Entradas
Saída
𝑨̅ .𝑩̅
A B 𝑨̅ 𝑩̅ S
1 0 0 1 1 1
2 0 1 1 0 0
3 1 0 0 1 0
4 1 1 0 0 0
22
=4
Entradas
Saída
𝑨. 𝑩̅̅̅̅̅
A B A.B S
1 0 0 0 1
2 0 1 0 1
3 1 0 0 1
4 1 1 1 0
A 0 0 1 1
B 0 1 0 1
S 1 0 0 0
A 0 0 1 1
B 0 1 0 1
S 1 1 1 0
f) Conclusão. Conclui-se que, negar as entradas de uma porta produz um resultado
diferente ao de negar a saída de uma mesma porta.

de 102
Desafio 5.2 – Resolução [AND OR NAND] Tendo em conta a expressão AB + 𝐴𝐶
e) Conclusão.
Resolução
=____
23
=8
Entradas
Saída
AB + 𝑨𝑪
1 0 0 0 0 0 1 1
2 0 0 1 0 0 1 1
3 0 1 0 0 0 1 1
4 0 1 1 0 0 1 1
5 1 0 0 0 0 1 1
6 1 0 1 0 1 0 0
7 1 1 0 1 0 1 1
8 1 1 1 1 1 0 1
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 1 1 1 1 1 0 1 1
f) Conclusão. A saída será 0 quando para a expressão AB’C, em todos os outros casos a
saída será 1.

de 102
Desafio 5.3 – Resolução [AND OR NAND] Tendo em conta a expressão A+B + 𝐴𝐶
e) Conclusão.
Resolução
=___8_
23
=8
Entradas
Saída
A+B + 𝑨𝑪
A B C A+B AC 𝑨𝑪 S
0 0 0 0 0 0 1 1
1 0 0 1 0 0 1 1
2 0 1 0 1 0 1 1
3 0 1 1 1 1 0 1
4 1 0 0 1 0 1 1
5 1 0 1 1 0 1 1
6 1 1 0 1 0 1 1
7 1 1 1 1 1 0 1
c) Desenharodiagrama temporal.A+B+ 𝑨𝑪
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 1 1 1 1 1 1 1 1
e) Conclusão.Qualquerque sejaaentradaa saída será sempre 1.

de 102
Desafio 6 – Resolução [OR NOT NOR] Tendo em conta a expressão 𝐴̅ +𝐵̅
Desafio 6.1 – Resolução [NOR] Tendo em conta a expressão 𝐴 + 𝐵̅̅̅̅̅̅̅̅
e) Conclusão.
Resolução
=__4__
22
=4
Entradas
Saída
𝑨̅ +𝑩̅
A B 𝑨̅ 𝑩̅ S
1 0 0 1 1 1
2 0 1 1 0 1
3 1 0 0 1 1
4 1 1 0 0 0
22
=4
Entradas
Saída
𝑨 + 𝑩̅̅̅̅̅̅̅̅
A B A+B S
1 0 0 0 1
2 0 1 1 0
3 1 0 1 0
4 1 1 1 0
c) Desenharoscircuitosnologisim.
d) Desenharos diagramastemporais.
A 0 0 1 1
B 0 1 0 1
S 1 1 1 0
A 0 0 1 1
B 0 1 0 1
S 1 0 0 0
e) Conclusão. Conclui-se que, negar as entradas de uma porta produz um resultado
diferente ao de negar a saída de uma mesma porta.

de 102
Desafio 6.2 – Resolução Tendo em conta a expressão A+B . 𝑨 + 𝑪
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
A+B . 𝑨 + 𝑪
A B C A+B A+C 𝑨 + 𝑪 S
0 0 0 0 0 0 1 0
1 0 0 1 0 1 0 0
2 0 1 0 1 0 1 1
3 0 1 1 1 1 0 0
4 1 0 0 1 1 0 0
5 1 0 1 1 1 0 0
6 1 1 0 1 1 0 0
7 1 1 1 1 1 0 0
d) Desenharo diagramatemporal.A+B . 𝑨 + 𝑪
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 0 1 0 0 0 0 0
e) Conclusão. A saída será 1 para a expressão A’BC’, todas as outras saídas serão 0.

de 102
Desafio 6.3 – Resolução Tendo em conta a expressão A.B . 𝑨 + 𝑪
e) Conclusão.
Resolução
=__8__
23
=8
Entradas
Saída
A.B . 𝑨 + 𝑪
A B C A.B A+C 𝑨 + 𝑪 S
0 0 0 0 0 0 1 0
1 0 0 1 0 1 0 0
2 0 1 0 0 0 1 0
3 0 1 1 0 1 0 0
4 1 0 0 0 1 0 0
5 1 0 1 0 1 0 0
6 1 1 0 1 1 0 0
7 1 1 1 1 1 0 0
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
S 0 0 0 0 0 0 0 0
f) Conclusão. A saída será sempre 0.

de 102
Comprovequea expressão 𝐀. 𝑩 + 𝑨. 𝐁 Equivaleà porta XOR
Porta Lógica- Logic GateXOR⊕
Desafio 7 – Resolução Tendo em conta a expressão 𝑺 = A. 𝐵 + 𝐴. B
Desafio 7.1 – Resolução Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵
e) Conclusão.
Resolução
=____
22
=4
Entradas
Saída
A. 𝐵 + 𝐴.B
A B 𝐴 𝐵 A. 𝐵 𝐴. B S
1 0 0 1 1 0 0 0
2 0 1 1 0 0 1 1
3 1 0 0 1 1 0 1
4 1 1 0 0 0 0 0
22
=4
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
1 0 0 0
2 0 1 1
3 1 0 1
4 1 1 0
A 0 0 1 1
B 0 1 0 1
S 0 1 1 0
A 0 0 1 1
B 0 1 0 1
S 0 1 1 0
f) Conclusão. 𝑆 = 𝐀. 𝑩 + 𝑨. 𝐁 é igual a 𝑆 = 𝐴 ⊕ 𝐵. Também conhecida como a porta ou exclusivo. A
saída só é 1 quando as entradas forem diferentes.

de 102
Comprovequea expressão A.B +𝑨.𝑩 Equivaleà porta XNOR
Porta Lógica- Logic GateXNOR ⊕
Desafio 8 – Resolução Tendo em conta a expressão S = A.B + 𝐴. 𝐵
Desafio 8.1 – Resolução Tendo em conta a expressão 𝑆 = 𝐴 ⊕ 𝐵
e) Conclusão.
Resolução
=____
22
=4
Entradas
Saída
A.B + 𝐴. 𝐵
A B 𝐴 𝐵 A. B 𝐴.𝐵 S
1 0 0 1 1 0 1 1
2 0 1 1 0 0 0 0
3 1 0 0 1 0 0 0
4 1 1 0 0 1 0 1
22
=4
Entradas
Saída
𝐴 ⊕ 𝐵
A B S
1 0 0 1
2 0 1 0
3 1 0 0
4 1 1 1
A 0 0 1 1
B 0 1 0 1
S 0 0 0 0
A 0 0 1 1
B 0 1 0 1
S 0 0 0 0
f) Conclusão. S = A.B +𝐴.𝐵 é igual a 𝑆 = 𝐴 ⊕ 𝐵. Também conhecida como a porta
coincidência. A saída é 1 quando as entradas são iguais.

de 102
Comprovação dos Teoremas de De Morgan
Desafio De Morgan – Resolução Tendo em conta os teoremas de De Morgan
Resolução
Ordem A B 𝐴 𝐵 𝐴. 𝐵 𝐴 + 𝐵 𝐴. 𝐵 𝐴 + 𝐵 𝐴 + 𝐵 𝐴. 𝐵
0 0 0 1 1 0 0 1 1 1 1
1 0 1 1 0 0 1 1 1 0 0
2 1 0 0 1 0 1 1 1 0 0
3 1 1 0 0 1 1 0 0 0 0
Teoremas
de “De
Morgan”
18 𝐴. 𝐵 = 𝐴 + 𝐵
19 𝐴 + 𝐵 = 𝐴. 𝐵
𝐴. 𝐵 = 𝐴 + 𝐵 𝐴 + 𝐵 = 𝐴. 𝐵

de 102
Desafio 9 – Resolução Tendo em conta a tabela de verdade
Resolução
=8
Ordem A B C S
Expressão
booleana
0 0 0 0 0
A’B’C+ A’BC+ AB’C’+ AB’C
1 0 0 1 1 A’B’C
2 0 1 0 0
3 0 1 1 1 A’BC
4 1 0 0 1 AB’C’
5 1 0 1 1 AB’C
6 1 1 0 0
7 1 1 1 0

de 102
Desafio 9.1 – Resolução Tendo em conta a tabela de verdade
Resolução
=______
Ordem A B C S
Expressão
booleana
0 0 0 0 1 A’B’C’
A’B’C’+ A’BC+ ABC’
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1 A’BC
4 1 0 0 0
5 1 0 1 0
6 1 1 0 1 ABC’
7 1 1 1 0

de 102
Resolução
=______
Ordem A B C S
Expressão
booleana
0 0 0 0 0
A’BC’+AB’C+ABC
1 0 0 1 0
2 0 1 0 1 A’BC’
3 0 1 1 0
4 1 0 0 0
5 1 0 1 1 AB’C
6 1 1 0 0
7 1 1 1 1 ABC

de 102
Resolução
=______
Ordem A B C D S
Expressão
booleana
0 0 0 0 0 0
A’BC’D’+ A’BCD’+ AB’CD+ ABCD’
1 0 0 0 1 0
2 0 0 1 0 0
3 0 0 1 1 0
4 0 1 0 0 1 A’BC’D’
5 0 1 0 1 0
6 0 1 1 0 1 A’BCD’
7 0 1 1 1 0
8 1 0 0 0 0
9 1 0 0 1 0
10 1 0 1 0 0
11 1 0 1 1 1 AB’CD
12 1 1 0 0 0
13 1 1 0 1 0
14 1 1 1 0 1 ABCD’
15 1 1 1 1 0
c) Desenharocircuitono logisim.(Utilizaportasde 3 ou maisentradas)

de 102
Desafio 10 – Resolução Tendo em conta o circuito lógico
Resolução
=____
c) Resolvera
saída na tabela
de verdade
Saída
A B C A’ C’ A’B A’B+C Expressão booleana
0 0 0 1 1 0 1
A’B+C’
0 0 1 1 0 0 0
0 1 0 1 1 1 1
0 1 1 1 0 1 1
1 0 0 0 1 0 1
1 0 1 0 0 0 0
1 1 0 0 1 0 1
1 1 1 0 0 0 0
A
B
C
S
Fase 1 Fase 2 Fase 3

de 102
Desafio 10.1 – Resolução Tendo em conta o circuito lógico
Resolução
=_8___
Saída
A B C A’ B’ A’+B’ 𝐴 + 𝐵 + 𝐶 𝐴 + 𝐵 + 𝐶 Expressão booleana
0 0 0 1 1 1 1 0
𝐴 + 𝐵 + 𝐶
0 0 1 1 1 1 1 0
0 1 0 1 0 1 1 0
0 1 1 1 0 1 1 0
1 0 0 0 1 1 1 0
1 0 1 0 1 1 1 0
1 1 0 0 0 0 0 1
1 1 1 0 0 0 1 0
A
B
C
S
S = …………….𝐴 + 𝐵 + 𝐶

de 102
Resolução
=_8___
Saída
A B C 𝐴 + 𝐵̅̅̅̅̅̅̅̅ A’ B+C A’B+C 𝐴 + 𝐵̅̅̅̅̅̅̅̅ + 𝐴′
𝐵 + 𝐶 Expressão booleana
0 0 0 1 1 0 0 1
𝐴 + 𝐵̅̅̅̅̅̅̅̅ + 𝐴𝐵 + 𝐶
0 0 1 1 1 1 1 1
0 1 0 0 1 1 1 1
0 1 1 0 1 1 1 1
1 0 0 0 0 0 0 0
1 0 1 0 0 1 0 1
1 1 0 0 0 1 0 1
1 1 1 0 0 1 0 1
C
B
S
A

de 102
Resolução
=_16___
𝐴𝐵. 𝐶𝐷
Ordem A B C D S
Expressão
booleana
Expressão booleana método da soma de
produtos (SdP)
0 0 0 0 0 1 A’B’C’D’
1 0 0 0 1 0
2 0 0 1 0 1 A’B’CD’
3 0 0 1 1 1 A’B’CD
4 0 1 0 0 1 A’BC’D’
5 0 1 0 1 0
6 0 1 1 0 1 A’BCD’
7 0 1 1 1 1 A’BCD
8 1 0 0 0 1 AB’C’D’
9 1 0 0 1 1 AB’C’D
10 1 0 1 0 1 A’BC’D
11 1 0 1 1 1 AB’CD
12 1 1 0 0 1 ABC’D’
13 1 1 0 1 0
14 1 1 1 0 1 ABCD’
15 1 1 1 1 1 ABCD

de 102
Comprovação da porta XOR
f) Conclusão.
Resolução
=____
11
Ordem A B S Soma de produtos A’B+AB’
0 0 0 0
A’B+AB’
0
1 0 1 1 A’B 1
2 1 0 1 AB’ 1
3 1 1 0 0
B 𝐵 B
Impossível simplificar, contudo a porta XOR
representa esta expressão
𝑆 = 𝐴 ⊕ 𝐵
Porta XOR
A 0 1
𝐴 0 0
0
1
1
A 1 1
2
0
3

de 102
f) Conclusão.
Resolução
=____
11.1
Ordem A B S Soma de produtos 𝐴 + 𝐵
0 0 0 1 A’B’
𝐴. 𝐵 + 𝐴𝐵 + 𝐴 . 𝐵
1
1 0 1 1 A’B 1
2 1 0 1 AB’ 1
3 1 1 0 0
B 𝐵 B
A’+B’
A 0 1
𝐴 0 1
0
1
1
A 1 1
2
0
3
𝐴𝐵 + 𝐴𝐵 + 𝐴 . 𝐵 Expressãobooleanaretiradadatabelade verdade
𝐴𝐵 + 𝐵(𝐴 + 𝐴) 14) Propriedade distributivaA.(B + C)= A . B + A . C
𝐴𝐵 + 𝐵(1) 5) Teorema 5 A+A̅=1
𝐴𝐵 + 𝐵 16) Identidadesauxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
𝐴 + 𝐵 Resultado
f) Conclusão.

de 102
e) Simplificarpelométododaálgebrabooleana
f) Conclusão.
Resolução
=____
0 0 0 0
A’B+AB’+AB
1 0 1 1 A’B
2 1 0 1 AB’
3 1 1 1 AB
B 𝐵 B
A+B
A 0 1
𝐴 0 0
0
1
1
A 1 1
2
1
3
𝐴𝐵 + 𝐴(𝐵 + 𝐵) 14) Propriedade distributivaA.(B + C)= A . B + A . C
𝐴𝐵 + 𝐴(1) 5) Teorema 5 A+A̅=1
𝐴𝐵 + 𝐴 16) Identidadesauxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
𝐵 + 𝐴 Resultado
f) Conclusão.

de 102
Comprovação da porta XNOR
e) Simplificarpelo métododaálgebrabooleana
f) Conclusão.
Resolução
=____
x
0 0 0 1 A’B’
A’B’+AB
1 0 1 0
2 1 0 0
3 1 1 1 AB
B 𝐵 B
Impossível simplificar, contudo a
porta XOR representa esta expressão
𝑆 = 𝐴 ⊕ 𝐵
Porta XNOR
A 0 1
𝐴 0 1
0
0
1
A 1 0
2
1
3

de 102
f) Conclusão.
Resolução
=____
X2
Ordem A B S Soma de produtos AB’+AB
0 0 0 0
AB’+AB
0
1 0 1 0 0
2 1 0 1 AB’ 1
3 1 1 1 AB 1
B 𝐵 B
A
A 0 1
𝐴 0 0
0
0
1
A 1 1
2
1
3
𝐴𝐵 + 𝐴𝐵 Expressãobooleanaretiradadatabelade verdade
𝐴(𝐵+ 𝐵) 14) Propriedade distributivaA.(B + C)= A . B + A . C
𝐴(1) 5) Teorema 5 A+A̅=1
𝐴 Resultado
f) Conclusão.

de 102
f) Conclusão.
Resolução
=____
d1) comprovar o
resultado na tabela
de verdade
Ordem A B C S Soma de produtos B’+A’
0 0 0 0 1
A’B’C’+A’B’C+A’BC’+A’BC+AB’C’+AB’C
1
1 0 0 1 1 1
2 0 1 0 1 1
3 0 1 1 1 1
4 1 0 0 1 1
5 1 0 1 1 1
6 1 1 0 0 0
7 1 1 1 0 0

de 102
A’B’C’+A’B’C+A’BC’+A’BC+AB’C’+AB’C Expressãobooleanaretiradada tabelade verdade
A’B’(C’+C)+A’B(C’+C)+AB’(C’+C) 14) Propriedade distributivaA.(B + C)= A . B + A . C
A’B’(1)+A’B(1)+AB’(1) 5) Teorema 5 A+A̅=1
A’B’+A’B+AB’
A’(B’+B)+AB’ 14) Propriedade distributivaA.(B + C)= A . B + A . C
A’(1) +AB’ 5) Teorema 5 A+A̅=1
A’+AB’ 16) IdentidadesAuxiliares 𝐴 + 𝐴. 𝐵 = 𝐴 + 𝐵
A’+B’ Resultado
f) Conclusão. Comprova-se que aexpressãobooleanaretiradadatabelapode serreduzidaaB’+A’.
B’+A’

de 102
e) Conclusão.
Resolução
=__8__
Ordem A B C S Soma de produtos A + C’
0 0 0 0 1 A’B’C’
A’B’C’ + A’B’C + AB’C’ +
AB’C + ABC’ + ABC
A+C’ = 0+1 = 1
1 0 0 1 0 X X
2 0 1 0 1 A’B’C A+C’ = 0+1 = 1
3 0 1 1 0 X X
4 1 0 0 1 AB’C’ A+C’ = 1+1 = 1
5 1 0 1 1 AB’C A+C’ = 1+0 = 1
6 1 1 0 1 ABC’ A+C’ = 1+1 = 1
7 1 1 1 1 ABC A+C’ = 1+0 = 1

de 102
d) Simplificarpelométodode karnaugh(Atenção às bordas)
A 00 01 11 10
𝐴 0 1
0
0
1
0
3
1
2
A 1 1
4
1
5
1
7
1
6
A + C’
e) Conclusão. A expressãoretiradadatabelanaalineab) pode serreduzidaaA+C’,comprovandouma elevada
simplificaçãodocircuitológicoe porconsequenciaumagrande reduçãonomaterial necessásioparaconcretização
deste objetivo.

de 102
Extrair expressões Booleanas de tabelas de verdade. (AC’+B’C)
f) Conclusão.
Resolução
=__8__
Ordem A B C S Soma de produtos B’C + C’A
0 0 0 0 0 X
A’B’C + AB’C’ + AB’C +
ABC’
X
1 0 0 1 1 A’B’C B’C + C’A = 1+0 = 1
2 0 1 0 0 X X
3 0 1 1 0 X X
4 1 0 0 1 AB’C’ B’C + C’A = 0+1 = 1
5 1 0 1 1 AB’C B’C + C’A = 1+0 = 1
6 1 1 0 1 ABC’ B’C + C’A = 0+1 = 1
7 1 1 1 0 X X
A 00 01 11 10
𝐴 0 0
0
1
1
0
3
0
2
A 1 1
4
1
5
0
7
1
6

de 102
B’C + C’A
A’B’C + AB’C’ + AB’C + ABC’ Expressãobooleanaretiradadatabelade verdade
B’C (A’+A) + AC’ (B’+B) Propriedade distributiva
B’C + AC’ TeoremaA+A’=1
f) Conclusão.
Se B for0 e C for1 ou se A for 1 e C for 0, a saída será1. Para as restantes hipótesesasaídaserá 0.

de 102
Criar circuitos lógicos com chips de circuitos integrados recorrendo a um
simulador online.
Circuitos lógicos com Chips de circuitos integrados
Desafio 13 – Resolução Utilizando o Chip 7408
a) Analisaa datasheetdochip7408 (corresponde àportaAND). http://www.electroschematics.com/8891/7408-
datasheet/
b) Constrói a expressãoA.Brecorrendoaosimuladoronline disponibilizadoem https://www.tinkercad.com
No final devesobterumcircuitosemelhante àfiguraabaixo.

Sistemas digitais - Exercícios de portas lógicas

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Semelhante a Sistemas digitais - Exercícios de portas lógicas

Semelhante a Sistemas digitais - Exercícios de portas lógicas (20)

Mais de Carlos Pereira

Mais de Carlos Pereira (20)

Último

Último (18)

Sistemas digitais - Exercícios de portas lógicas