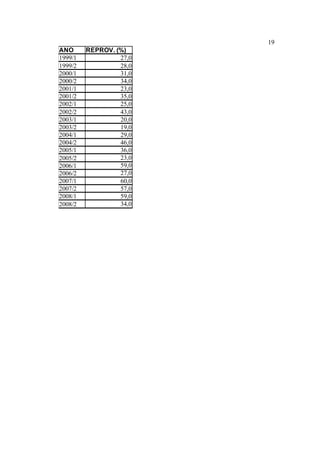
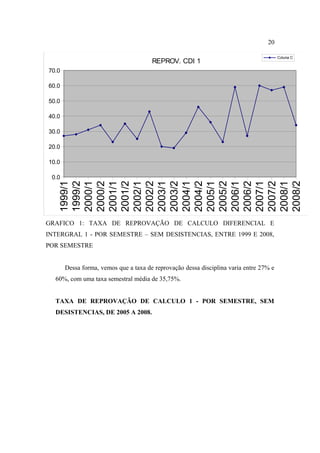
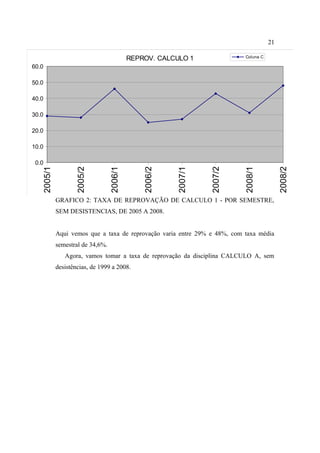
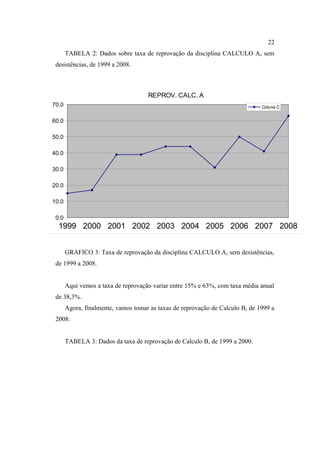
Este documento apresenta uma proposta de metodologia para o ensino de Cálculo utilizando a perspectiva lógico-histórica. Ele discute as altas taxas de reprovação em disciplinas de Cálculo, analisa as dificuldades de aprendizagem dos alunos e traça o desenvolvimento histórico dos conceitos fundamentais do Cálculo. A proposta sugere estudar a história da matemática para compreender a evolução dos conceitos e utilizar problemas históricos no ensino, ao invés do método tradicional. O objetivo é que








































































![78
infinitesimais que então surgiram pudessem se organizar e disciplinas autônoma, - o
Cálculo Diferencial e Integral.
Numa das versões, AVILA (1985), mostra que:
x
F ( x ) = ∫ f (t ) dt
a
É uma primitiva de f, isto é, F’(x) = f(x). Outra versão
equivalente desse teorema afirma que se G é uma
primitiva qualquer da função f, então:
b
G (b) − G ( a ) = ∫ f (t ) dt ;
a
Ou ainda, como f ( x) = G ' ( x),
b
G (b) − G ( a ) = ∫ G ' (t ) dt.
a
Evidentemente, tudo isso é válido no pressuposto de que
f(x) e G’(x) sejam funções contínuas no intervalo [a, b}.
Porém, no século XVII, quando o Cálculo ainda se
encontrava em estágio embrionário, não havia uma
preocupação explicita com a noção de continuidade,
mesmo porque o conceito de função era também muito
restrito. Por função se entendia uma correspondência
entre variáveis, sempre dada por fórmulas ou expressões
analíticas, como:
y=3x²-7x+1, y= x x ² + , etc.
1
E a noção de continuidade só começaria a aparecer no
século XVIII.
De acordo com THOMAS (2002), para Gottfried Wilhelm Leibniz (1646 –
1716), uma curva era um polígono com um número infinito de lados, onde ele fez y
representar uma ordenada da curva e dx a distância infinitesimal de uma abscissa para a
próxima, isto é, a diferença entre abscissas "sucessivas". Então disse que representaria a
área de uma figura pela soma de todos os retângulos [infinitesimais] limitados pelas](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-78-320.jpg)
![79
ordenadas e diferenças das abscissas, e assim representaria em seu cálculo a área da
figura por ò y dx.
Leibniz tomou o "S" alongado para a integral do latim summa e d do latim
differentia, e estas têm permanecido nossas notações de cálculo mais básicas desde
então, segundo BOYER (1989).
Segundo BOS e BARON (1974, p. 52), algumas idéias importantes que
fundamentaram a invenção do cálculo por Leibniz, foram:
• O interesse de Leibniz pelo simbolismo e pela notação vinculando à sua
idéia de uma linguagem simbólica geral;
• O reconhecimento de que somar sequências e tomar as suas diferenças são
operações inversas e que, semelhantemente, a determinação de áreas e a de
tangentes são operações inversas.
No inicio do século XVIII, segundo ÁVILA (1985), Leonhard Euler (1707 –
1783), publicou livros que estabeleceram padrões definitivos ao Cálculo e exerceram
influencia por um século. Então, segundo volume de uma dessas obras – “Introduction
in Analysin Infinitorum”, de 1848, ele distingue funções continuas de descontínuas.
Assim, por contínua, ele entende uma função dada por uma única expressão analítica,
como:
y = sen x, y = x2 + 1 ou y = log x.
É descontínua uma função dada por várias expressões analíticas, porém cujo
gráfico é uma curva única, sem interrupções, o que difere do que hoje entendemos por
descontinuidade.
Já THOMAS (2002), nos diz que a idéia moderna de uma função contínua,
independente de qualquer fórmula, foi iniciada em 1791 por Louis-François Arbogast
(1759 – 1803): "A lei de continuidade consiste em que uma quantidade não pode passar
de um estado [valor] para outro [valor] sem passar por todos os estados
intermediários [valores] ...". Esta idéia tornou-se rigorosa em um panfleto de 1817 por
Bernhard Bolzano (1781 - 1848) e é conhecida agora como o Teorema do Valor
Intermediário. Dessa forma, as funções descontínuas no sentido moderno só foram](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-79-320.jpg)
![80
introduzidas na comunidade matemática e científica por Joseph Fourier (1768 – 1830)
no seu famoso Analytical Theory of Heat (Teoria Analítica do Calor, 1822).
Segundo THOMAS (2002), Augustin Louis Cauchy (1789 – 1857) assumiu a
reforma total do cálculo para seus alunos de engenharia na École Polytechnique na
década de 1820, a integral era uma de suas pedras Fundamentais.
Já BOS e BARON (1974), diz que a concepção de integração como o inverso da
diferenciação, de Newton e de Bernoulli, era geralmente aceita no século XVII. Então,
Cauchy apresentou outro enfoque para a integração, considerando-a como soma. Ele
definiu a integral como um somatório que tende a um limite.
Seguindo BOS e BARON (1974), é dito que:
Uma vez que a integração não é mais definida como o
inverso da diferenciação, o Teorema Fundamental do
Cálculo não um corolário da definição da integração,
mas deve ser provado. O teorema fundamental afirma que
a integração e a diferenciação são operações inversas.
Para sermos mais precisos, ele afirma que se f é uma
função continua e considerarmos a função F definida por:
b
F ( x ) = ∫ f ( x ) dx, entãoF ' = f .
a
Segundo THOMAS (2002, p. 11), Cauchy definiu a integral de qualquer função
contínua no intervalo [a, b] sendo o limite da soma das áreas de retângulos finos. Dessa
forma sua primeira obrigação era provar que este limite existia para todas as funções
contínuas sobre o intervalo dado. Infelizmente, embora Cauchy tenha usado o Teorema
do Valor Intermediário, não conseguiu seu objetivo porque não observou dois fatos
teóricos sutis, mas cruciais. Ele não tinha noção das falhas lógicas no seu argumento e
prosseguiu para justificar o Teorema do Valor Médio para Integrais e para provar o
Teorema Fundamental do Cálculo para funções contínuas.
Já TUMELERO e MUSIAL (2003, p. 7), dizem que no século XVIII, a ênfase
era posta na idéia de função dada por uma expressão analítica. Também é dito que os
conceitos de derivada e integral, como os de funções e continuidade, eram insuficientes
para lidar com os novos problemas que surgiam no final do século. Então, Cauchy foi o](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-80-320.jpg)
![81
primeiro a introduzir a integral analiticamente. Em seu “Résumée” de 1823 ele define
integral como o limite de somas do tipo:
Ou seja, de acordo com TUMELERO e MUSIAL (2003), quebrou o domínio da
integração em subintervalos de tamanho arbitrário por uma divisória e
calculou a área como o limite de:
,
então quando n aumenta, esta soma se aproxima da área do trapezóide definido sob o
gráfico de f, estabelecendo assim sua existência para toda a função contínua.
Portanto, TUMELERO e MUSIAL (2003), concluem a respeito da integral
segundo Cauchy que a integral assim definida dispensa com a restrita concepção de que
f tenha uma função analítica. Basta que a função f seja contínua para que exista F tal
que F’(x) = f(x); F é a integral definida de f num intervalo [a; b].
Ainda no século, apareceu Georg Friedrich Bernhard Riemann (1826-1866), que
seguiu os trabalhos de Dirichilet, de tal forma que segundo TUMELERO e MUSIAL
(2003, p. 8), o ponto de partida de Riemann é a questão não resolvida por Dirichlet em
1829:
O que significa dizer que uma função é integrável? Ao
contrário de Cauchy, que se restringiu, em suas
considerações, as funções que são contínuas, ou, no
máximo, seccionalmente contínuas, Riemann não faz
outra hipótese sobre a função a ser integrada, além da
exigência de que suas “somas de Riemann”, convirjam. E
estabelece, a partir daí, critérios para a integrabilidade
que caracterizam completamente a classe das funções
integráveis.](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-81-320.jpg)

![83
Aqui vale destacar que nos cursos de Cálculo Diferencial e Integral 1, é estudado
ao conceito de integral de Riemann. Entretanto, como a história da matemática não pára
e continua dinâmica, vamos apenas dar uma breve pincelada em tal contribuição.
Assim, TUMELERO e MUSIAL (2003), dizem que em 1901, Lebesgue
publicou uma nota na qual propunha um novo conceito de integral contendo como caso
particular a de Riemann, conseqüentemente a de Cauchy, eliminando várias deficiências
dessas integrais, e em particular, dando uma resposta mais geral sobre a validade da
fórmula de Newton- Leibniz. Este novo conceito vai permitir, por exemplo, estender a
classe das funções integráveis: Um exemplo simples de função ƒ: [0, 1] → R integrável
à Lebesgue e não integrável à Riemann é:
Em resumo, podemos falar sobe o desenvolvimento dos conceitos de Cálculo,
subdividindo-os em 4 grupos, a saber:
• Funções:
Como vimos anteriormente, de acordo com YOUSCHKEVITCHI (1981), citado
por OLIVEIRA (1997), existem três etapas principais do desenvolvimento de funções,
que podem ser resumidos da seguinte forma:
• Antiguidade: Etapa no curso no qual o estudo de diferentes casos de
dependência entre duas quantidades ainda não isolou as noções de gerais de
quantidades variáveis e de funções.
• Idade Média: Nesta etapa, as noções, são pela primeira vez, e de maneira
precisa, expressas sob uma forma geométrica e mecânica, mas durante a
qual, como na antiguidade, cada caso concreto de dependência entre duas
quantidades, são definidas por uma descrição verbal, ou por um gráfico, de
preferência fórmula.
• Período Moderno: No curso, da qual, no fim do século XVI, e durante o
século XVII, as expressões analíticas de funções começam a prevalecer; a](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-83-320.jpg)


![86
• Bonaventura Cavalieri (1598--1647), que desenvolveu uma teoria de
indivisíveis.
• Pierre Fermat (1601 – 1665) desenvolveu uma técnica para encontrar as áreas
sob cada uma das "parábolas de ordem superior" usando retângulos estreitos inscritos e
circunscritos para levar ao método de compressão.
• Por volta da década de 1640, a fórmula geral para a integral de parábolas de
ordem superior era conhecida de Fermat, Blaise Pascal (1623-1662), Gilles
Personne de Roberval (1602--1675), René Descartes (1596--1650),
Torricelli, Marin Mersenne (1588--1648) e provavelmente outros.
Já Newton escreveu seu ensaio entre 1691 e 1693, onde ele montou uma tabela
extensa de integrais de funções algébricas um tanto complicadas, e para curvas as quais
não podia desenvolver fórmulas de integração, inventou técnicas geométricas de
quadratura. Usando o Teorema Fundamental do Cálculo, Newton desenvolveu as
técnicas básicas para avaliar integrais usadas hoje em dia, incluindo os métodos de
substituição e integração por partes.
De acordo com THOMAS (2002), para Gottfried Wilhelm Leibniz (1646 –
1716), uma curva era um polígono com um número infinito de lados, onde ele fez y
representar uma ordenada da curva e dx a distância infinitesimal de uma abscissa para a
próxima, isto é, a diferença entre abscissas "sucessivas". Então disse que representaria a
área de uma figura pela soma de todos os retângulos [infinitesimais] limitados pelas
ordenadas e diferenças das abscissas, e assim representaria em seu cálculo a área da
figura.
Já Augustin Louis Cauchy (1789 – 1857) assumiu a reforma total do cálculo
para seus alunos de engenharia na École Polytechnique na década de 1820, onde a
integral era uma de suas pedras Fundamentais.
Ainda no século, apareceu Georg Friedrich Bernhard Riemann (1826-1866), que
seguiu os trabalhos de Dirichilet, de tal forma que o ponto de partida de Riemann é a
questão não resolvida por Dirichlet em 1829, dando uma grande contribuição ao estudo
das integrais.
Após a contribuição de Riemann, destacamos o trabalho Henri-Léon Lebesgue
(1875 – 1941).](https://image.slidesharecdn.com/tccfinalailton-121014095358-phpapp02/85/Tcc-final-ailton-86-320.jpg)






























































