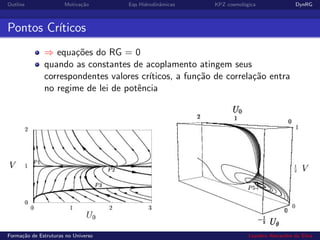
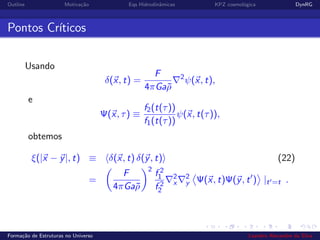
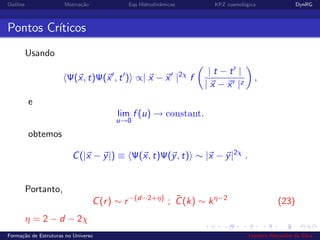
1) O documento discute a formação de estruturas no universo, modelando o processo como o crescimento estocástico de uma superfície.
2) A equação de Kardar-Parisi-Zhang (KPZ) é proposta para descrever a evolução do perfil desta superfície em expansão.
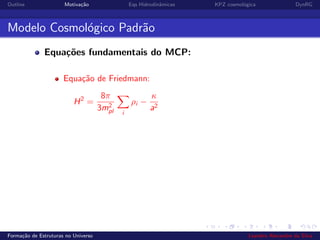
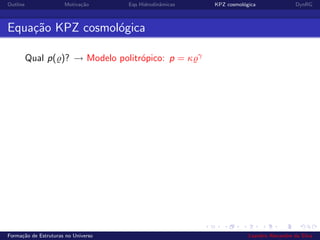
3) A equação KPZ cosmológica é derivada para modelar especificamente a formação de estruturas no universo.






































![Outline Motiva¸c˜ao Eqs Hidrodinˆamicas KPZ cosmol´ogica DynRG
Equa¸c˜ao KPZ cosmol´ogica
´E poss´ıvel reescrever a eq. KPZ cosmol´ogica com coeficientes
constantes? Sim!
∂ψ
∂t
= f1(t)ν 2
ψ +
1
2
f2(t)λ( ψ)2
+
f3(t)
T
ψ + η , (15)
f1(t) =
1
ν
F(t)p ( b(t))
4πGa2(t) b(t)
,
f2(t) =
1
λa(t)
,
f3(t) = [F(t) − H(t)]T .
Forma¸c˜ao de Estruturas no Universo Leandro Alexandre da Silva](https://image.slidesharecdn.com/lssf-130501131752-phpapp01/85/Formacao-de-estruturas-46-320.jpg)





![Outline Motiva¸c˜ao Eqs Hidrodinˆamicas KPZ cosmol´ogica DynRG
Equa¸c˜oes do Grupo de Renormaliza¸c˜ao
dU0
d log s
= (2 − d)U0 +
U2
0
4dV 3
[d + 3(dV − 2)]
+
U2
θ
4V 3+4θ
sec(2πθ)(1 + 4θ)
+
U0Uθ
4dV 3+2θ
(1 + 2θ) sec(πθ) ×
[2d − 8θ + 3((d − 2ρ)V − 2)] (20)
dUθ
d log s
= (2 − d + 2ρ + 4θ)Uθ +
U0Uθ
4dV 3
(dV − 2)(3 + 2θ)
+
U2
θ
4dV 3+2θ
(1 + 2θ) sec(πθ) ×
[−8θ + ((d − 2ρ)V − 2)(3 + 2θ)]
dV
d log s
= (V − 1)[2 +
1
4dV 3
[(dV − 2)U0
+((d − 2ρ)V − 2)V −2θ
(1 + 2θ) sec(πθ)Uθ]]
Forma¸c˜ao de Estruturas no Universo Leandro Alexandre da Silva](https://image.slidesharecdn.com/lssf-130501131752-phpapp01/85/Formacao-de-estruturas-52-320.jpg)