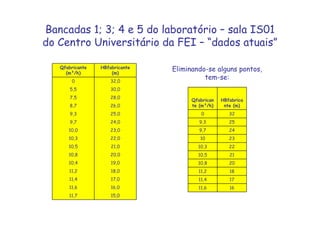
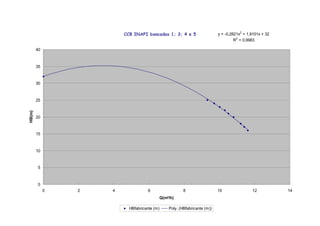
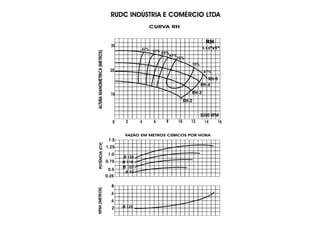
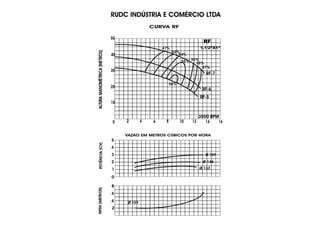
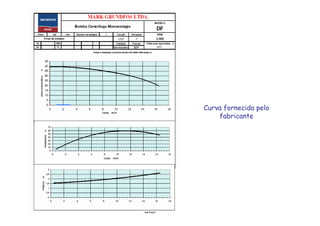
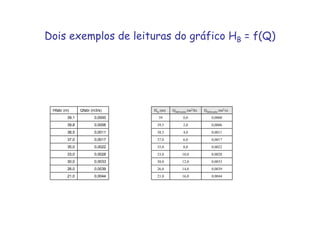
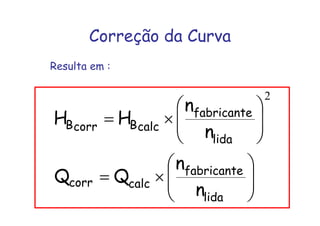
O documento discute o ponto de trabalho de uma bomba hidráulica, que é obtido pela interseção da curva característica da instalação com a curva característica da bomba. Isso porque neste ponto a bomba é capaz de fornecer a carga manométrica necessária para a vazão requerida pelo sistema. O documento também destaca a importância de se obter o ponto de trabalho o mais próximo possível do ponto de projeto para garantir eficiência, e como fatores como a rotação real podem alterar a curva característica da

1. Quinta aula de complemento
11/03/2008

2. Ao se projetar uma bomba hidráulica visa-se,
especificamente, o recalque de determinada
vazão em certa altura manométrica (HB) de
modo a se obter o máximo rendimento (ponto de
projeto do fabricante). Entretanto, esta bomba
poderá ser posta a recalcar vazões (Q) maiores
ou menores que aquela para a qual foi projetada
mudando, com a variação de Q, a altura
manométrica (HB), a potência necessária ao
acionamento (NB) e o rendimento (ηΒ) (Carvalho,
D. F. Instalações elevatórias: bombas. Belo
Horizonte:IPUC, 1977, 355p).

3. Pelo exposto anteriormente,
estuda-se o ponto de trabalho de
uma bomba

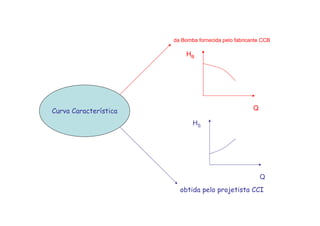
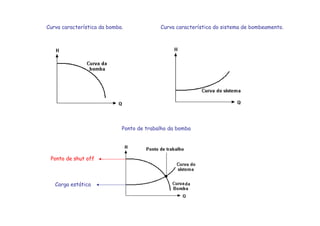
4. O ponto de trabalho de uma bomba
hidráulica é obtido pelo cruzamento
da Curva Característica da Instalação
[CCI] com a Curva Característica da
Bomba [CCB], isto porque neste ponto
a bomba é capaz de fornecer ao
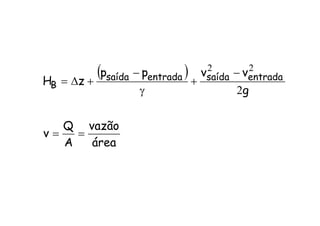
fluido a carga manométrica (HB)
precisamente igual a que o fluido
necessita para percorrer a instalação
hidráulica com uma vazão Q em
regime de escoamento permanente.

5. QCurva Característica
da Bomba fornecida pelo fabricante CCB
obtida pelo projetista CCI
HB
HS
Q

6. Curva característica da bomba. Curva característica do sistema de bombeamento.
Ponto de trabalho da bomba
Carga estática
Ponto de shut off

7. No ponto de trabalho, deve-se ter:
1. Qτ ≥ fator de segurança * Qdesejada, onde o
fator de segurança deve ser no mínimo 1,1 e
se possível não superior a 1,20;
2. HBτ ≥ HBpp que é obtido através da equação
da CCI para a vazão de projeto (Qprojeto =
fator de segurança * Qdesejada);
3. ηBτ deve ser o mais próximo possível do
rendimento máximo;
4. NPSHrequerido parâmetro importante para
análise do fenômeno de cavitação.

8. Exemplo de CCB

9. Bancadas 1; 3; 4 e 5 do laboratório – sala IS01
do Centro Universitário da FEI – “curvas
antigas”
1,5471410,8
1,455216,510,3
1,45418,79,5
1,35520,59
1,1556237,2
1,155246,8
154255,8
0,95225,54,8
0,84725,94
4525,952,8
260
NPSH(m)ηB (%)HB (m)Q(m³/h)

10. Bomba INAPI - bancadas 1; 3; 4 e 5
y = -0,1618x
2
+ 0,7361x + 26
R
2
= 0,9805
y = -0,5759x
2
+ 8,5169x + 24,205
R
2
= 0,9029
y = -0,001x
2
+ 0,1177x + 0,3517
R
2
= 0,9971
0
10
20
30
40
50
60
0 2 4 6 8 10 12
Q(m³/h)
HB(m);rend(%)eNPSHr(m)
= rendimento NPSHreq Poly. (=) Poly. (rendimento) Poly. (NPSHreq)

11. Bancadas 1; 3; 4 e 5 do laboratório – sala IS01
do Centro Universitário da FEI – “dados atuais”
11,7
11,6
11,4
11,2
10,4
10,8
10,5
10,3
10,0
9,7
9,3
8,7
7,5
5,5
0
Qfabricante
(m³/h)
15,0
16,0
17,0
18,0
19,0
20,0
21,0
22,0
23,0
24,0
25,0
26,0
28,0
30,0
32,0
HBfabricante
(m)
Eliminando-se alguns pontos,
tem-se:
1611,6
1711,4
1811,2
2010,8
2110,5
2210,3
2310
249,7
259,3
320
HBfabrica
nte (m)
Qfabrican
te (m³/h)

12. CCB INAPI bancadas 1; 3; 4 e 5 y = -0,2821x
2
+ 1,9101x + 32
R
2
= 0,9983
0
5
10
15
20
25
30
35
40
0 2 4 6 8 10 12 14
Q(m³/h)
HB(m)
HBfabricante (m) Poly. (HBfabricante (m))

13. Estamos procurando entrar em
contato com a INAPI para
esclarecer qual das curvas
está correta.
INAPI (85) 3299-7400
CE

14. Bancada 2 do laboratório – sala IS01 do Centro
Universitário da FEI
VAZÃO EM METROS CÚBICOS POR HORA
5,07,510,011,011,812,013,214,01.5RH-5
2,04,58,510,211,011,813,01.0RH-4
1,06,08,39,210,011,03/4RH-3
4,06,58,09,010,01/2RH-2
282624222018161412108CVMODELO
ALTURA MANOMETRICA TOTAL EM METROS

16. Bancada 6 do laboratório – sala IS01 do Centro
Universitário da FEI
VAZÃO EM METROS CÚBICOS POR HORA
6,09,211,512,813,53.0RF-7
7,09,610,511,011,512,012,512,82.0RF-6
5,07,08,09,09,510,010,511,012,01.5RF-5
454035302826242220181614CVMODELO
ALTURA MANOMETRICA TOTAL EM METROS

18. Bancadas 7 e 8 do laboratório – sala IS01 do
Centro Universitário da FEI

19. Curva fornecida pelo
fabricante

20. Dois exemplos de leituras do gráfico HB = f(Q)
0,004421,0
0,003926,0
0,003330,0
0,002833,0
0,002235,0
0,001737,0
0,001138,5
0,000639,8
0,000039,1
Qfabr (m3/s)Hfabr (m)
0,004416,021,0
0,003914,026,0
0,003312,030,0
0,002810,033,0
0,00228,035,0
0,00176,037,0
0,00114,038,5
0,00062,039,5
0,00000,039
Qfabricante (m3/s)Qfabricante (m3/h)Hm (m)

21. Portanto para um projeto
eficiente é fundamental que se
obtenha o ponto de trabalho o
mais próximo possível do ponto
de trabalho real e para se
obter esta situação deve-se
refletir sobre o que pode
causar variações na CCB?

22. Geralmente a CCB pode ser alterada:
1. alterando-se o diâmetro do rotor;
2. alterando-se a rotação da bomba;
3. bombeando fluidos viscosos, ou
seja, com viscosidades superiores a
20 mm²/s;
4. com o envelhecimento da tubulação
e/ou bomba

23. Nesta experiência o objetivo é
constatar a variação da CCB
com a rotação real.

24. Na verdade todas as curvas
anteriores são nominais, isto
porque foram fornecidas para
uma rotação nominal, portanto
devem ser corrigidas em
função da rotação real, que
deve ser obtida com o auxílio
de um tacômetro.

26. A experiência é análoga a
realizada no curso básico de
mecânica dos fluidos, com
exceção da leitura da rotação
para cada posição da válvula
controladora de vazão.

27. A determinação da rotação de
uma bomba é feita pela a
expressão:
2éolaboratórioparaquepolos,denúmerop
Hz60éBrasilnoque,freqüênciaf
p
f
n
→
→
×
=
120

28. Se o número de pólos do motor elétrico for 2,
temos a rotação n= 3600 rpm e se o número de
pólos do motor elétrico for 4, temos a rotação n=
1800 rpm.
Devido ao escorregamento, a rotação cai na faixa
de 3500 rpm para bombas com motores elétricos
de 2 pólos, e na faixa de 1750 rpm para Bombas
com motores elétricos de 4 pólos. Os fabricantes
de bombas geralmente adotam uma rotação de n
= 3500 rpm para bombas com motores elétricos
com 2 pólos e n= 1750 rpm para bombas com
motores elétricos com 4 pólos e com estes
valores de rotações eles levantam as CCB’s das
mesmas.

29. No nosso laboratório o motor
da bomba é de 2 pólos o que
equivale a dizer que a bomba
ensaiada tem a rotação n =
3500 rpm.

30. Na experiência aplicaremos a
equação da energia entre a
entrada e a saída da bomba,
onde já consideramos o
coeficiente de energia cinética
(α) igual a 1,0, isto pelo fato do
escoamento ser turbulento

31. saída
entrada

32. ( )
área
vazão
A
Q
v
g
vvpp
zH entradasaídaentradasaída
B
==
−
+
γ
−
+∆=
2
22

33. Observe que, quando a válvula estiver totalmente
aberta, teremos máxima vazão(Q) e mínima pressão
de saída, quando estivermos com a válvula
totalmente fechada, teremos máxima pressão de
saída e nenhuma vazão, portanto já temos dois (2)
pontos, o de máxima pressão de saída (Q = 0) e o de
mínima pressão de saída (Q = Qmáx).
Entre estes 2 pontos acrescentaremos mais 6
pontos para a realização do ensaio. A cada leitura
de pressão, volume e tempo, devemos ler a rotação
do eixo do motor que é feita com o auxilio de um
aparelho chamado tacômetro.

34. válvula controladora de vazão
A bancada de laboratório
representa uma instalação de
recalque.

35. pressão de saída
pressão de entrada
válvula globo

36. A rotação será diferente em cada
leitura, diferente de 3500 rpm,
que foi a rotação especificada
pelo fabricante. Esta diferença
de rotação é devido ao
escorregamento e a variação de
tensão na rede elétrica. A
rotação deve ser lida pelo
tacômetro.

38. Correção da Curva da Bomba
Condição de semelhança completa :
Dxn
Q
3
R
=φφ1 = φ2
Coeficiente de Vazão
ψ1 = ψ2
Coeficiente Manométrico
Dxn
Hg
2
R
2
B×
=ψ

39. Correção da Curva
Resulta em :
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×=
lida
fabricante
calccorr
lida
fabricante
calcBcorrB
n
n
QQ
n
n
HH
2

40. Tabela de dados
Vazão
8
7
6
5
4
3
2
1
Unidades
Rotação(n)Pm2Pm1Ensaio