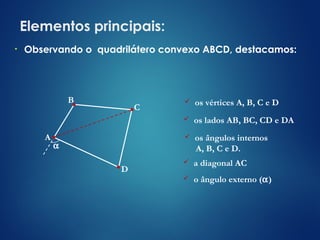
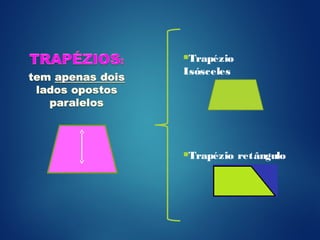
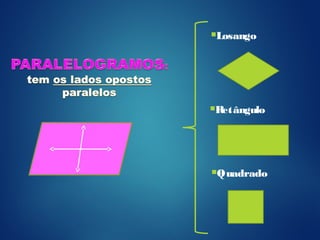
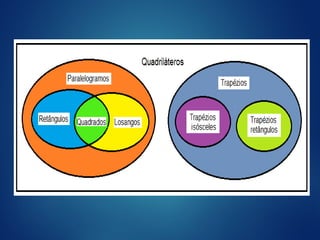
Um quadrilátero é uma figura plana formada por quatro pontos não colineares e os segmentos que os conectam. Os ângulos internos de um quadrilátero somam sempre 360°. Existem diferentes tipos de quadriláteros, como trapézios, losangos, retângulos e quadrados, classificados de acordo com a forma e propriedades dos lados e ângulos.

1. QUADRILÁTEROS

2. Dado quatro pontos A, B, C e D não-colineares,
chama-se quadrilátero ABCD a figura plana
constituída pela reunião dos segmentos AB, BC, CD
e DA e pelos pontos interiores à região que eles
determinam.
A
B
C
D
A
B
C
D
Quadrilátero convexo Quadrilátero côncavo

3. Elementos principais:
• Observando o quadrilátero convexo ABCD, destacamos:
 os vértices A, B, C e D
 os lados AB, BC, CD e DA
 os ângulos internos
A, B, C e D.
 o ângulo externo (α)
A
B
C
D
α
 a diagonal AC

4. SOMA DOS
ÂNGULOS
INTERNOS

5.  SAI∆ ABC = 180°
 SAI∆ ADC = 180°
 SAI ABCD = 180° + 180°A
B
C
D
 SAI ABCD = 360°
A SOMA DOS ÂNGULOS INTERNOS DE UMA SOMA DOS ÂNGULOS INTERNOS DE UM
QUADRILÁTERO É 360°QUADRILÁTERO É 360°

6. Classificação
dos
quadriláteros

8. Trapézio
Isósceles
Trapézio retângulo

9. Losango
Retângulo
Quadrado

11. Bidu em:
“DEPENDE DO ÂNGULO QUE SE VÊ”

15. Referências:
•IEZZI, Gelson; MACHADO, Antonio;
DOLCE, Osvaldo. Geometria Plana-
Conceitos básicos. 1ª edição. São
Paulo: Atual, 2008.
• DANTE, Luiz Roberto. Matemática.
Ensino Médio. Projeto Múltiplo. São
Paulo: Ática: 2014.
• DOLCE, Osvaldo. Fundamentos de
Matemática elementar 9: geometria
plana. 8ª ed. São Paulo: Atual, 2005.
• GIOVANNI, José Rui; PARENTE,
Eduardo. Aprendendo Matemática. São
Paulo: FTD, 2007
•Prof. Jorge.
< http://slideplayer.com.br>

16. EXERCÍCIOS DO LIVRO PG 52 A 58